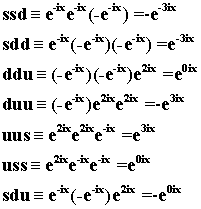5.4.2.1.3.Семейства

5.4.2.1.3.Семейства

"Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг).

М.И. Беляев, 2015г,©

МОНАДНЫЕ СЕМЕЙСТВА

1. О ФУНКЦИОНАЛЬНОЙ ПРИРОДЕ ЖИВОТВОРЯЩЕГО КРЕСТА

Принцип Абсолюта, зафиксированный в кресте и освященный древними легендами и религиями не является какой-то мистикой. Он отражает самые важные стороны любых двойственных отношений и характеризуется не только структурным, но и функциональным аспектом. Функциональная природа креста характеризует закон сохранения двойственных отношений, существующих в кресте. Крест одновременно отражает эволюцию двух асимметричных двойственных пар, взаимодействующих, синхронизированных друг с другом и обменивающихся друг с другом асимметричными качествами и свойствами. Крест отражает закон подобия двух его перекладин. Записывая закон сохранения двойственных отношений в кресте в виде пропорции

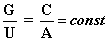
мы приходим к схеме, изображенной на рис. 1,

рис.1

из которой видно, что равновесное состояние между всеми вершинами креста регулируется правилом рычага, известного каждому из школьного курса физики: выигрыш в силе - проигрыш в расстоянии. Здесь имеют место две пары двойственных отношений G/U и C/A, и отражающими закон сохранения двойственных отношений, который будет иметь место только тогда, когда эти отношения будут подобными. Это значит, что при изменении любого значения, все другие будут немедленно скорректированы (и перенормированы), с тем, чтобы между ними подобие не нарушалось. Данное тождество является одним из самых фундаментальных в мире. поскольку отражает двойственную природу этого природного рычага. Поэтому и механизмы его проявления являются многоуровневыми и всеобщими. В механике этот закон подобия перекладин креста известен как правило рычага - проигрываешь в расстоянии - выигрываешь в силе. Поэтому по аналогии с механикой соотношение вида

G=UC/A или C=GA/U

можно называть силой монадного рычага. В экономике это сотношение д.э.н. Забродоцкий справедливо называет приницпом природного операционализма. В финансовом менеджменте сила монадного рычага ассоциируется с понятиями сила операционного рычага и сила финансового рычага и т.д. При этом отношение этих сил G/C во многих приложениях также имеет большое значение, т.к. оно является нормированным отражением подобия сил в кресте. Так, в экономике оно известно как ценовая эластичность.

Закон подобия двойственных пар образует крест с двумя коромыслами, которые синхронно связаны между собой. Это приводит к тому, что если в какой-либо паре изменится соотношение плеч коромысла, то это немедленно приведет в движение весь механизм с целью достижения нового равновесного состояния. Эти две пары двойственных отношений (крест) в пространстве образуют тетраэдр. Эти тетраэдры могут формировать более сложные кресты. Так, на рис. 3 изображен крест, составленный из L- и D- асимметричных тетраэдров, разделенных друг от друга «стеной», которая может играть роль мембраны, через которую и осуществляется обмен между двумя асимметричными тетраэдрами. Объединение любых двух соседних асимметрических тетраэдров в звездный тетраэдр приведет к образованию перекладины креста. Тогда оставшиеся два тетраэдра образуют другую перекладину этого нового, более сложного креста. На более высоком уровне иерархии из этой монадной формы могут образовываться еще более сложные кресты, но во всех крестах будут отражаться рекурсивное проявление свойств рычага.

Рис. 3

Рассмотрим действие этого рычажного механизма. Каждая перекладина креста отражает собственное измерение и имеет собственный масштаб. Переход от одной перекладины креста к другой характеризуется коэффициентом подобия перекладин, характеризуя относительные масштабы рычага креста. Последовательно осуществляя переходы, мы получаем механизм природного операционализма, описанный д.э.н. Забродоцким , в основе которого лежат операции деления и умножения. Производя деление, мы определяем коэффициент подобия для одного рычага коромысла, умножая коэффициент на плечо, мы получаем относительный момент, действующий во второй перекладине. Заключительное деление приводит нас к определению коэффициента подобия при переходе к первой перекладине. Последний рисунок показывает рекурсивное свойство рычага. Один крест порождает другие, более сложные по структуре, но механизм функционирования любого креста остается прежним. Подобный обмен асимметричными качествами и свойствами - основное взаимодействие в природе. Он многообразен, но и у креста лишь четыре основных проявления, которые задают параметры (вершины). Ниже будет обосновано, что каждый крест может быть может представлять собой одно из взаимосвязанных звеньев двойной спирали генетического кода соответствующего двойственного отношения, лежащего в основе креста. Рассмотрим действие этого рычажного механизма. Положим, что к₀=1, к₁=1, к₂=1 . Тогда

<…/ к₀ =G; GL=A; A/ к₁=U; UH=C; C/ к₂=G; GL=A; A/ к₁=U; UH=C; C/ к₂=G; …>

Каждая операция деления переводит двойственное отношение в новое измерение, сдвинутое на 90 градусов и определяет коэффициент подобия для этого измерения, который используется для инвариантных преобразований между соответствующими плечами рычажного механизма.

Из этих рекурсивных последовательностей непосредственно видно, что возврат к первоначальному значению мы получим только после двойного обхода по кресту. Действительно, при первом переходе мы осуществляем поворот на 90⁰, при втором переходе этот поворот будет составлять только 180⁰. В наиболее общем виде циклический механизм взаимопереходов по кресту и свойства всех этих переходов показан на рис. 10. Суть подобной функциональности не зависит от сложности структуры самого креста. Она не зависит и от сфер человеческой деятельности. Этот механизм действует в любой отрасли знаний. И происходит это потому, что в основе этого механизма лежит Единый Периодический закон эволюции двойственных отношений. На рис. 4 приведена еще одна схема эволюции двойственных отношений.

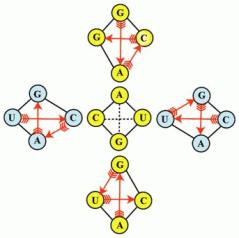Рис. 4

На данном рисунке в центре находится исходный крест (тетраэдр), который может порождать четыре новых креста (тетраэдра). Данный рисунок не претендует на достоверность. Но он иллюстрирует чрезвычайно важные принципы, отражающие самые важные свойства двойственных отношений. В центре этого рисунка находится совершенная монадная форма, которая способна породить более совершенную монадную форму, характеризуя симметрию и асимметрию порождаемых более сложных тетраэдров.

Механизм эволюции двойственного отношения можно пояснить следующей схемой.

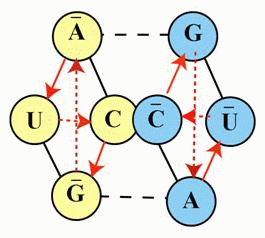Рис. 5

Представленная на рисунке модель представляет собой механизм эволюции дуадной пары, в которой исходное двойственное отношение является антагонистическим (), состоящим из "частицы" и "античастицы". Следовательно, мы можем вести речь о двух триадах частиц (), порождающих дискретный набор двойственных частиц. В физике элементарных частиц аналогом данному семейству экономических частиц может служить мезонное семейство, состоящее и двух кварковых триад (триада + антитриада). "Частицы" данного дуадного семейства, порождаемого антагонистической парой , можно записать в следующем виде

Данная последовательность выражает сущность и смысл эволюции любого антагонистического двойственного отношения .

Подобные двойственные отношения имеют место и во всех сферах Бытия. Так, тесные двойственные отношения в экономике связывают рубль и доллар. Полная аналогия наблюдается между свойствами элементарных и «экономических» частиц позволяет характеризовать не только последовательные этапы эволюции двойственного отношения, но и их заряд. На первых этапах эти взаимоотношения носят ярко выраженный дульный характер. Дальнейшая эволюция приводит эти отношения к некоторому равновесному состоянию, которое собственно и является целью любой эволюции. В противном случае двойственное отношение разрушается.

Однако в монадном кресте существуют и взаимодополнительные (не антагонистическое) отношение (СС). В этом случае мы получим совершенно другие семейства частиц, порождаемых триадами .

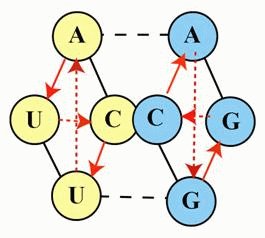Рис. 6

Здесь животворящий крест двойственных отношений переродился в новое семейство частиц, характеризующих эволюцию гармонических отношений. Аналогом данному семейству в физике элементарных частиц может служить барионное семейство, порождаемое триадами

Таким образом, каждая частица, порожденная исходной монадой, усиливает мощь своего рычага за счет последовательного соединения с родственной ей частицей, поэтому переход в новое измерение не приводит к негативным последствиям. При этом уже изначально двойственное отношение СС является триединым, т.е. такое отношение характеризуется взаимодополнительностью, полезностью для обеих полюсов двойственного отношения. Эта взаимодополнительность характеризуется тем, что на каждом ребре квадры стоят разноцветные, но одноименные монадные кварки.

Однако такое семейство не рождается на пустом месте. Оно является естественным продуктом эволюции мезонного (дуадного) семейства. Только тогда, когда эволюция мезонного семейства будет завершена и будет сформирована совершенная монадная форма, только тогда эта новая совершенная форма сможет сформировать новую истинно нейтральную, триединую частицу, которая породит двойственную пару и станет родоначальницей нового триплетного (триединого) семейства.

Однако независимо от типа семейства (дуадное или триплетное) все семейства обладают одним чрезвычайно важным свойством.

Переход с одного полюса перекладины креста на противоположный полюс равносилен операции умножения, а переход с одной перекладины креста к другой (переход в другое измерение) можно отождествить с операцией деления.

Даже поверхностный анализ рисунков 5 и 6 позволяет говорить о том, что любое семейство двойственных отношений всегда формирует двойную спираль. Поэтому попытка людей строить, например, только спираль расширенного воспроизводства, в основе которой лежит операции умножения неизбежно породит негативную зазеркальную спираль, которая будет строится Природой на основе операции деления и, в конечном итоге, неизбежно приведет к краху такого расширенного воспроизводства. Поэтому любой механизм хозяйствования, как и любой другой, независимо от его природы, должен содержать двойную спираль. Только в этом случае, когда операции умножения и деления будут синхронизированы между собой во времени и пространстве, только тогда можно всерьез говорить об эффективности существующих механизмов хозяйствования. Естественно, что данный функциональный аспект креста будет справедлив во всех сферах Бытия человека, а не только в экономике.

Этот функциональный аспект креста механизм отражает единую формулу подобия, которая используется Природой во всех инвариантных преобразованиях, при фазовых переходах из одного измерения в другое, из одного собственного пространства в другое, из одной совершенной формы в другую.

Свойства двойственный отношений в тетраэдрах (в том числе и звездный) тетраэдров можно проиллюстрировать следующим образом. Рассмотрим следующие пары двойственных отношений

Составляя из этих пар тетраэдры и соединяя их вместе, мы получим

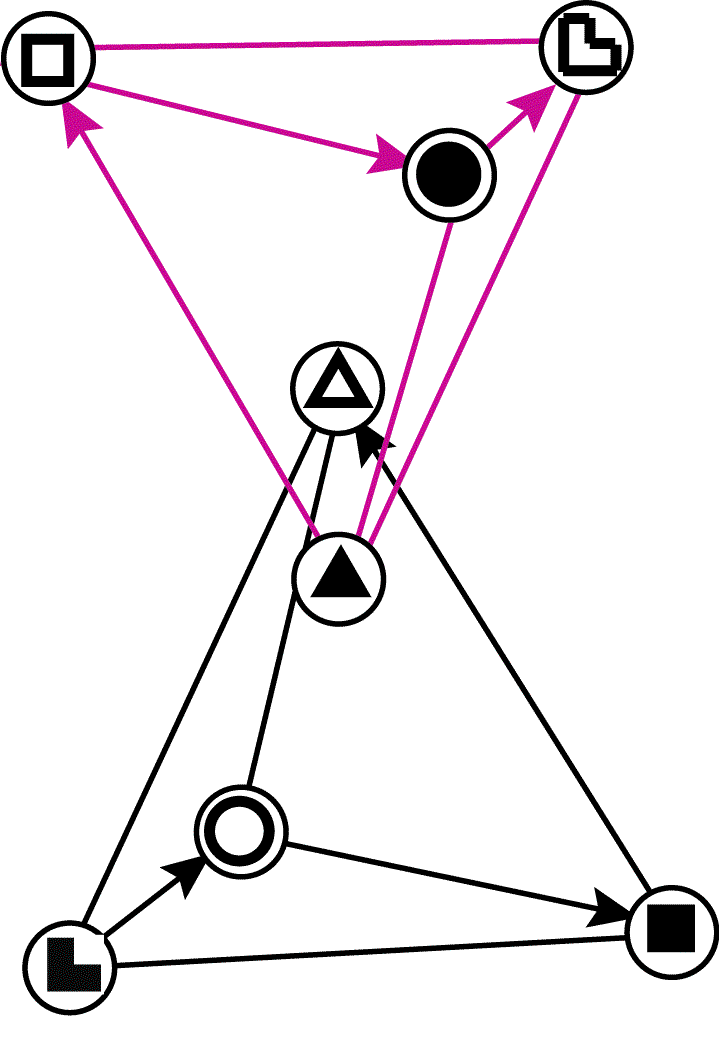
Рис. 7

Каждая из вершин полученного звездного тетраэдра обладает валентностью, т.е. свойством присоединять к себе взаимодополнительную вершину. Это приводит к тому, что возникает пространственная кристаллическая фигура из восьми шести звездных тетраэдров, в центре которых находится еще одна двойственная пара. В нашем случае это пара "-", которая является основателем соответствующего семейства "звездных частиц". Эта пара является осью симметрии для всех других двойственных отношений звездного тетраэдра. Это ось его "вращения", характеризующая его выделенное направление в пространстве. Поэтому можно говорить о том, что исходная двойственная пара представляет собой некоторый специфический вектор, который по аналогии со спином в физике элементарных частиц, можно называть монадным спином.

Нетрудно видеть, что данная пара ничем не отличается от других взаимодополнительных пар, что ее полюса-вершины тоже могут являться смежными вершинами соседних звездных тетраэдров. Особенность этой пары в том, что через нее как бы происходит связь семейства " звездных частиц", порождаемой парой "-" с семействами "звездных частиц", порождаемых другими двойственными парами

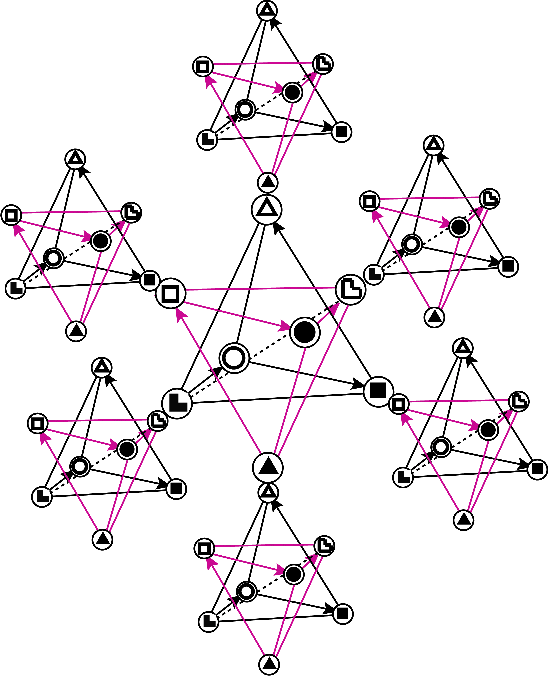Рис. 8

Из рисунка видно, что все звездные тетраэдры, порождаемые исходной монадой, являющейся звездным тетраэдром, имеют свой собственный спин. Может быть в этом причина, что в физике элементарных частиц каждое семейство элементарных частиц имеет свой собственный спин?

Таким образом, свойства "звездных" семейств, порождаемых тем или другим двойственным отношением, полностью определяются "генными" свойствами этого двойственного отношения. Так, если это двойственное отношение порождается двумя взаимодополнительными тетраэдрами, то в вершинах звездного тетраэдра этого семейства могут располагаться тетраэдры (не звездные). Это двойственное отношение составляет ось симметрии всей конструкции, ее осью вращения. Ниже, при анализе свойств двойственных отношений в дуадных и триплетных монадных семействах будут обоснованы правила порождения всех частиц соответствующих монадных семейств. Эти правила оказываются едиными для всех монадных семейств и они определяются правилами "крещения" (подробнее).

2. ЖИВОТВОРЯЩИЙ КРЕСТ И ДРЕВНИЙ ЦВЕТОК ЖИЗНИ

Многоуровневость животворящего креста и его двойственность порождают Единый Универсальный закон эволюции живой и неживой Природы. Свойства этого закона самым подробным образом описаны на страницах данного сайта. Многоуровневость и вездесущность проявления Единого закона порождает Цветок Жизни (рис. 11). Удивительная симметрия и гармония рисунка далеко не случайны. Из древних легенд Востока до нас доходят поистине мистические свойства этого Цветка. Так, эти источники утверждают, что Цветок содержит в себе все известные законы и все известные формулы. И эти утверждения не голословны. Совокупность узлов рисунка характеризуется сотовой структурой, состоящей из шестигранников. Иерархичность и инвариантность построения узора Цветка позволяют сделать вывод о том, что каждый узел в этом Цветке также может быть Цветком Жизни (рис.9).

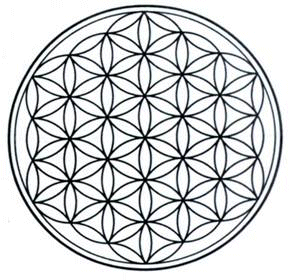
Рис. 9

Эти рисунки дают более полное представление о механизмах формирования и функционирования структуры, изображенной на рис. 8.

Выше было показано, что куб порождается двумя животворящими крестами, и естественно, что узоры Цветка Жизни оказываются как бы вышиты из крестов. На последнем рисунке в центре показана одна секция Цветка Жизни, в которой есть длина и ширина. Из этих сегментов и построен весь Цветок. Каждый кружок в этом Цветке является двойственным отношением, или даже Цветком Жизни. Поэтому даже два внешние два круга в этом Цветке далеко не случайны. Они имеют очень простой смысл: все многообразие Жизни порождается двойственным отношением. Поэтому все свойства в Цветке определяются свойствами двойственных отношений, порождаемых его узлами.

На странице "Геном атомов" приведено обоснование механизмов формирования ГЕНОМА Периодической системы химических элементов и было показано, что вся Периодическая система химических элементов представляет собой целостную "вышивку крестом". Она соткана из крестов и по своей структуре представляет собой самую совершенную форму ГЕНОМА МИРОЗДАНИЯ.

Узоры Цветка жизни также обладают определенными функциональными свойствами. Все узлы Цветка Жизни синхронизированы между собой. В одной гексаде значение узла вычисляется с использованием операции умножения, а в другой, сопряженной в этом узле с первой, значение этого же самого узла должно получаться с использованием операции деления. Таким образом, все "взаимоотношения" между узлами Цветка взаимосвязаны и даже строго синхронизированы. Может быть это чудо Природы? Нет, это чудо носит строго эволюционный преемственный характер. Изначальное двойственное отношение порождает третью, равновесную вершину, которая фиксирует двойственное отношение. Рождается триада, рождается закон сохранения двойственного отношения. При изменении значения любой вершины, закон сохранения приводит к мгновенной коррекции значений двух других вершин, используя операцию умножения, или деления. Напомним, что все известные законы сохранения по своей структуре отражают взаимоотношения в триаде (например, закон Ома и др.). В тетраэдре (кресте) эти законы сохранения отражаются в принципах природного операционализма, а в звездном тетраэдре эти законы сохранения приобретают уже завершенный вид, отражаемый в свойствах Единого Универсального закона.

Поэтому Цветок Жизни является в высшей степени самосогласованным "часовым" механизмом, в котором законы сохранения двойственных отношений интегрированы в Единый закон сохранения Цветка Жизни. При любом изменении любого значения, в любом узле, под влиянием внешних возмущений, все значения остальных узлов Цветка будут немедленно и мгновенно скорректированы. Таким образом, Цветок Жизни отражает Единый закон сохранения всего функционального механизма Цветка. Кроме того, рис. 14 свидетельствует о том, что Цветок Жизни является пространственной фигурой, многослойной фигурой.

Построить Цветок жизни для конкретной пары экономических или социальных отношений -не простое дело. Но этот Цветок будет создан, то мы получим всесторонне гармонизированный единый самосогласованный механизм функционирования этого отношения. Цветок Жизни это та бессмертная матрица, зная которую, по любому узлу может восстановить полностью всю матрицу, т.к. принципы ее построения голографичны.

4. О ЖИВОТВОРЯЩЕМ КРЕСТЕ И МОНАДНЫХ КВАРКАХ

        Из трех последовательно соединяемых вершин тетраэдра они всегда будут лежать в одной плоскости. Две вершины на одной прямой и третья - на прямой, ортогонально первой прямой. При этом будет справедливо утверждение, что обход вершин тетраэдра осуществляется таким образом, что любые три соседних вершины должны лежать в одной плоскости. Именно эти свойства проявляются в плоских гексадах монадной фигуры, которые следует рассматривать как проекцию монадной фигуры (звездного тетраэдра) на выбранную плоскость.

    Но совершенная монадная форма не рождается сама по себе, стихийно. Этот процесс происходит также с использованием животворящего креста (рис. 10).

Рис. 10

   В этом кресте перекладина "" является запретной. Поэтому обход по кресту характеризуется схемами, изображенными на рисунке. И только тогда, когда завершится такой обход по кресту, когда установятся постоянные "дистанционные" связи между вершинами "", только тогда возникает прямая связь между этими вершинами и возникает двойственная пара, рождающая совершенную монадную форму. Таков функциональный механизм, порождающий совершенную монадную форму (звездный тетраэдр).

    Выше мы уже рассмотрели последовательность формирования монадных частиц в пространственной монадной форме. Для дуадных семейств эта последовательность характеризуется следующим рисунком.



Рис. 11

    Для триплетных семейств эта последовательность порождения частиц характеризуется следующей схемой.

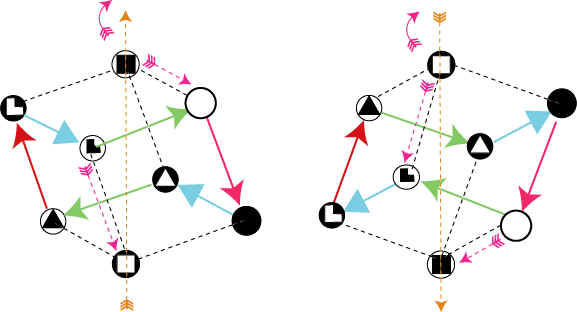Рис. 12

    Эти рисунки наглядно показывают, как в монадной форме рождается правило обхода "по кресту".

        Правило " обхода по кресту" во всех монадных семействах одно и тоже, независимо от типа и свойств монадных частиц, содержашихся в том или ином монадном семействе.

    Все двойственные частицы на одном ребре соединены последовательно (одна перекладина, но со сдвигом по фазе на 90⁰. Поэтому переход к следующей перекладине будет осуществляться уже в ортогональной плоскости.

        В результате такого обхода, каждая вершина фонадной формы оказывается способной порождать собственное трехмерное подпространство, порождать собственный цветной спектр, смесь которых и будет порождать бесцветную вершину (нейтральную монадную частицу). При этом в зависимости от смешиваемой "дозы" спектральных цветов, мы можем для этой частицы получить "белый" или "черный" цвет.

3. О ПРАВИЛАХ ПОРОЖДЕНИЯ СЕМЕЙСТВ ИЗ МОНАДНЫХ КВАРКОВ

В процессе эволюции «от простого - к сложному» будут рождаться новые типы монадных кварков, но по своим свойствам они будут аналогичны своим предшественникам. Во-первых, этому будет способствовать существующий природный механизм перенормировки монадных кварков, рассмотренный выше, в соответствии с которым всегда можно осуществить инвариантные переходы из одного собственного пространства в другое и пересчет соответствующих индивидуадных собственных значений, фиксирующих его эволюционное прошлое (собственный «вес» кварка, его ориентацию в пространстве, заряд, цвет и некоторые другие характеристики). Заряд может характеризовать знак собственного значения недостающей «скрытой массы». В этом случае природа может следить за периодическим изменением знака своего «веса». Так, ниже. при анализе семейств элементарных частиц. будет показано. что в процессе эволюции частиц их масса также периодически изменяется. Вначале она увеличивается, а затем уменьшается практически возвращается в некоторую окрестность первоначального значения. Заряд также последовательно из отрицательного трансформируется в нейтральный, затем в положительный, затем снова «обнуляется» и, наконец, на следующем витке спирали снова меняется на противоположный, но при этом частица переходит уже на следующий уровень эволюции.

Все монадные семейства порождаются с использованием одних и тех же правил.

1. Выбирается двойственная пара (одна "перекладина" креста), например,.

2. Используя полученную перекладину, формируется первая "проявленная" частица второй перекладины креста, формируя тем самым "рычаг креста". Эта же частица будет характеризовать и внутреннюю структуру исходной двойственной пары. свойства этой частицы будут иметь определяющее значение для свойств всего семейства монадных частиц. Так, полагая, что внутренняя структура будет тождественна триаде и формируя для нее зеркальный отпечаток, мы получим, например

Данная двойственная пара характеризует единичную эластичность двойственного отношения. Это первые и последние частицы монадного семейства, имеющие нейтральный заряд, т.к. составляют центральную ось "вращения" монадной формы.

3.Теперь, зная свойства первой и последней "проявленной " частицы второй "перекладины" и зная тип формируемого семейства, нетрудно построить остальные с "рычаги креста" и сформировать соответствующее семейство. Вначале формируется один монадный тетраэдр, а затем строится второй, монадный тетраэдр, который является по отношению к первому зеркальным. При этом все монадные частицы располагаются между полюсами двух зеркальных триад.

Таким образом, рассмотренные выше монадные формы и их свойства, позволяют определить не только типы монадных форм (их многоуровневую структуру), но определить свойства и правила порождения для всех вершин той или иной совершенной монадной формы (звездного тетраэдра).

Выше мы описали функциональную природу животворящего креста. Но животворящий крест является плоскостью. Он представляет собой проекции векторов совершенной монадной формы (звездный тетраэдр, или куб) на "экваториальную плоскость" оси симметрии (вращения) этой монадной формы. Рассмотрим теперь функциональную природу самой монадной формы, используя цвета радуги (рис.12-1).

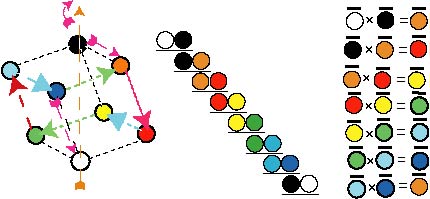Рис. 12-1

На данном рисунке показана последовательность обхода по пространственному кресту и правила векторного умножения соответствующих ортогональных векторов, проходящих через вершины той или иной грани монадной фомы. Может быть и сами правила векторного умножения, повсеместно используемые во всех прикладных науках, были порождены этим пространственным животворящим крестом? Более того, из векторной таблицы умножения видно, что для того, чтобы каждый очередной цвет оказался нормированным, достаточно после операции умножения выполнить операцию деления, например

Из последнего выражения видно, что смысл перехода к следующему измерению заключается в нормировании результата векторного умножения путем деления векторного произведения на себя. В результате мы получаем нормированную монадную форму, характеризующую нормированное собственное пространство трех измерений.

3.1. ДУАДНЫЕ МОНАДНЫЕ СЕМЕЙСТВА

Дуадные семейства порождаются в соответствии с простым правилом: каждая частица порождается двойственным отношением между двумя любыми вершинами звездного тетраэдра, соединенных между собой ребрами монадной формы. Исключением являются двойственное отношение, которое образует ось симметрии вращения монадной формы. Таких осей в звездном тетраэдре всего 4. Эти центральные двойственные отношения и будут составлять собственно монаду, которая является первым и последним элементом эволюции монадной формы. Действительно, это единственное двойственное отношение, составленное из одноименных (но взаимодополняемых) вершин звездного тетраэдра. Тогда, размещая эти центральные двойственные отношения в центре гексады эволюции соответствующей монады, мы получим четыре набора монадных кварков, в каждом из которых имеются монадные кварки и антикварки, образующих соответственно монадные триады и антитриады.

Поскольку каждая монада в своей монадной форме определяет ось вращения формы, то следовательно эта ось является вектором, по которому можно определить направление вращения звездного тетраэдра и его значение (расстояние между полюсами монады). Применительно к монаде будем такой вектор называть монадным спином, соответствующей монадной формы, или просто спином.

О правилах и последовательности порождения дуадных элементырных частиц первое представление дает следующий рисунок.

Из этого рисунка непосредственно видно, что элементарные частицы порождаются слиянием двух соседних частиц, принадлежащих к разным тетраэдрам.

На нижерасположенных рисунках приведены все соответствующие семейства частиц, порожденных тем или иным кварковым набором соответствующей монады.

Рис. 13

Из рисунка видно, как реализуется замкнутый цикл обхода дуадной монадной формы по кресту.

Рис. 14

Рис. 15

Рис. 16

Проанализируем более подробно свойства полученных монадных частиц дуадного семейства (рис.16). В каждом звездном тетраэдре каждая его вершина имеет в своем окружении ("видит") только три противоположные (взаимодополняющие) вершины (рис. 17).

Рис. 17

Группируя вершины по парам, получим следующие парные последовательности

Рис. 18

Таким образом, как только будет создана совершенная монадная форма, то в ней возникают новые двойственные связи, а их общее число не будет превышать 24.

Эта матрица, отражает многие важные свойства монадной формы. Можно предположить, что уже в самом ближайшем будущем эта матрица откроет свои самые сокровенные тайны, о которых сегодня можно только догадываться. Эта матрица, отражая закономерности, присущие животворящему кресту, откроет людям новые тайны, подобно тому, как сегодня Периодическая система химических элементов отдает одну тайну за другой. Отметим пока только некоторые, самые очевидные свойства этой матрицы. Из смысла устанавливаемых такой матрицей связей, нетрудно понять, что звездный тетраэдр трансформируется в куб. При этом все полученные двойственные пары разделяются на две группы, имеющие взаимодополняющую структуру (рис. 16).

Рис. 19

Из смысла полученной монадной формы (куб) следует, что двойственные отношения в такой монадной форме могут быть отображены в форме квадр. Каждая квадра будет соответствовать двойственным парам, формирующим соответствующую грань куба из соответствующих монадных кварков. Число квадр будет соответствовать числу граней куба.

При анализе дуадной монадной формы следует иметь ввиду особенности, отраженные на рисунках ниже, для каждой двойственной пары. На первом рисунке (слева) на каждой грани располагаются три одноцветные вершины и одна вершина другого цвета. На втором рисунке (справа) на каждой грани также находится по два одноцветных монадных кварка.

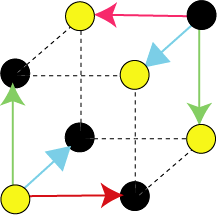Рис. 20

Первый рисунок характеризует самодостаточность тетраэдров в монадной форме. Во втором рисунке имеет место их взаимопроникновение друг в друга.

Эта схема двойственных взаимоотношений между вершинами тетраэдров может рассматриваться как отношения с внутренней двойственностью, т.к. это уже целостная система. В соответствии с этой схемой можно выстроить следующую схему двойственных отношений для пары " ".

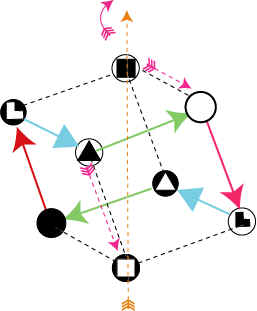Рис. 21

Здесь стрелками показан уже замкнутый цикл обхода этих монадных форм по "кресту".

Основная особенность обхода монадной формы "по кресту" заключается в том, что этот путь обхода является единственным, поскольку кварки двойственной пары не участвуют в обходе. Каждая перекладина формируется только единственным образом, путем сопряжения разноцветных кварков.

Таким образом, в каждом монадном семействе звездного тетраэдра имеется всего восемь двойственных отношений, включая и саму монаду. И это свойство может иметь, например, в физике элементарных частиц, очень существенное значение, так как поможет понять связь кварков, стоящих в центре монады (ось вращения монадного кристалла) с другими монадными кварками. Полученные монадные частицы позволяют сделать некоторые первые выводы об их главных свойствах. Так, каждое двойственное отношение характеризует не только свою структуру, но и несет информацию о направлении своей эволюции (по часовой стрелке или против). Поэтому первый монадный кварк, стоящий в монадной частице следует считать доминирующим. Однако эта информация является еще не полной, т.к. она не содержит в себе информацию о спине монады, породившей то или иное двойственное отношение. С точки зрения математики первый монадный кварк в монадной частице характеризует только направление обхода монадной формы (по часовой или против часовой стрелки), в то время как монадный спин характеризует вектор оси вращения монадной формы. Если учесть, что полюса каждой монады являются взаимодополнительными по своим свойствам, то из рисунков можно непосредственно определить общее число "монадных частиц", которое будет равно 32. Это число будет характеризовать максимальное число измерений звездного тетраэдра. Следовательно, свойства той или иной монадной частицы определяется не только структурными свойствами, не только их различием в порядке следования в частицах с одинаковой структурой, но и их принадлежностью к тому или иному монадному семейству, к той или иной квадре. В каждом монадном семействе, порождаемой той или иной монадой, каждой монадной частице соответствует ее античастица.

3.4. ТРИАДНЫЕ МОНАДНЫЕ СЕМЕЙСТВА

Рассмотренные выше свойства двойственных отношений формировать триады, позволяет сделать вывод о существовании монадных форм, в которых монада, порождающая звездный тетраэдр ее эволюции, представляет собой двойственное отношение, в котором внутренняя структура каждого монадного кварка является триадной. Какова может быть природа такого явления. Кто и как порождает триады в монадном кристалле? Чудес в природе не бывает. Все происходит в соответствии с законами природы и, в первую очередь, с Единым Периодическим законом эволюции живой и неживой природы.

Поэтому уже исходная монада, которая является осью симметрии (вращения) монадного кристалла, уже должна содержать в себе соответствующие "гены", характеризующие свойства их внутренней структуры (кварковый заряд, спин и др.). Внутренняя структура исходной монады должна отражать в явном виде ее дуадность или триадность (триединство). Может быть эти свойства отражаются уже в самой структуре монадного кристалла, которая характеризуется дуадностью, либо триадностью связей между вершинами? Во всяком случае следует еще раз обратить самое пристальное внимание на одно чрезвычайно важное свойство свойство звездного тетраэдра. Он способен к перестройке своей внутренней структуры (звездный тетраэдр, или куб). Каждая из этих структур характеризует иные свойства двойственных отношений, которые могут порождать иные монадные семейства. В монадном кубе каждая "черная" вершина связывается по ребрам с тремя "белыми" вершинами, а каждая "белая" - с тремя "черными", т.е. каждая вершина как бы проявляет триплетность, а вершины исходной монады, являясь вершинами оси вращения монадного кристалла, становятся приобретают триадность. В результате такого соединения в монадном кубе получается 6 квадр, в которых одноцветные (черные либо белые) монадные кварки размещаются на диагоналях куба, образуя "перекладины креста" и определяя функциональные свойства тождественных преобразований между сторонами монадного куба. Следовательно, подобные обходы "по кресту" можно применять и к прямоугольникам. Подобная структура и является причиной порождения монадных триадных семейств.

Теперь, используя полученные выше правила порождения частиц из монадных кварков, построим триадные монадные семейства для соответствующих осей симметрии звездного триплетного тетраэдра.

Рис. 22

Из рисунка видно, как осуществляется обход пространственной монадной формы, как формируются животворящие кресты и как происходит переход с одной его "перекладины" на другую. Поскольку этот звездный тетраэдр триадный, то и центральное двойственное отношение будет состоять из двух взаимодополняющих монадных частиц, которые получаются в соответствии с правилами формирования единой двойной цепочки. Нетрудно понять, что внутренняя структура монадных кварков, формирующих исходную двойственную пару будет по своей внутренней структуре совпадать со структурой соответствующей монадной триады. В нашем случае внутренняя структура монады будет тождественна выражению

Каждая из этих монадных частиц характеризует структуру нейтральной монадной частицы. Если эти частицы объединить в единую двойственную пару, то мы получим единственную истинно нейтральную монадную частицу. Аналогичные структуры нейтральных и истинно нейтральных монадных частиц получаются и для других двойственных пар, являющимися другими осями симметрии монадного кристалла (рис. 7-9).

На следующем рисунке приведены схемы обхода по кресту при вращении монадной формы вокруг ее оси симметрии (двойственной пары "")

Рис. 23

Эта схема отражает обход звездного тетраэдра по кресту как по часовой стрелке, так и против часовой. При этом в случае, когда такие тетраэдры сопрягаются вместе с противоположным монадным спином, то обход "по кресту" оказывается синхронизированным. На этой схеме пунктирными стрелками обозначены связи исходной монады (пары "") с другими двойственными парами (вершинами звездного тетраэдра). Пунктирными стрелками показана связь исходной двойственной пары с самой первой вершиной, порождаемой данной монадой, с данным монадным спином. Эта схема поясняет также принципы порождения всех нейтральных монадных частиц и истинно нейтральных частиц (см. ниже о зарядах монадных частиц). Аналогичные схемы можно построить и для дуадных монадных семейств.

Если в качестве исходного двойственного отношения будет выбрана другая двойственная пара, то в общем случае мы можем получить следующие монадные семейства.

Рис. 24

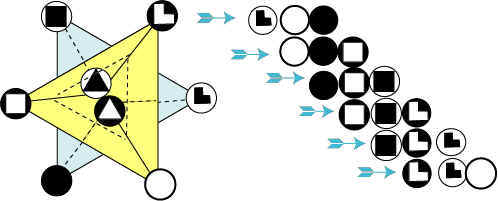Рис. 25

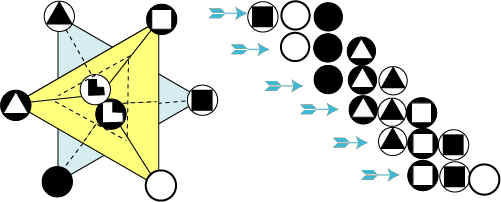Рис. 26

Из рисунков видно, что каждая следующая частица получается также по алгоритму Фибоначчи (каждый третий член ряда равен сумме двух его предыдущих членов), если считать два одноименных монадных кварка за одну частицу.

Из рисунка 26 можно сделать предварительный вывод о том, что в мире монадного царства властвует Порядок. Здесь нет хаоса. Каждая частица монадныхь семейств знает свое место, а их совокупность (восемь частиц), формирует монадное семейство, являющееся основой (ГЕНОТИПОМ) соответствующего МОНАДНОГО ГЕНОМА, из которых ткется узор ГЕНОМА ВСЕЛЕННОЙ(Геном Вселенной).

5. О СВОЙСТВАХ ЧАСТИЦ МОНАДНЫХ СЕМЕЙСТВ

Рассмотрим некоторые важные свойства, которые будут присущи всем частицам, на всех уровнях иерархии материи.

5.1. СВОЙСТВА ЧАСТИЦ ДУАДНОГО СЕМЕЙСТВА

На рисунке, представленном ниже, приведена гексада эволюции дуадного монадного семейства.

Рис. 27

Главная особенность свойств дуадных частиц заключается в том, что здесь частицы "белого" и "черного" цветов расположены строго последовательно относительно друг друга, таким образом, что каким бы путем мы ни обходили вершины куба, мы никогда не встретим две одноцветные частицы, идущие непосредственно друг за другом. На рисунке справа эта же особенность проявляется и в порядке следования разноименных частиц -ни одного рядом стоящего одноименного символа в дуадной гексаде нет. При этом цвет символов также имеет значение. Два символа одного и того же цвета не повторяются.

При этом важно отметить, что цвет частиц и цвет символов могут комбинироваться. ВЫ зависимости от этого могут существовать два подтипа дуадного семейства. В одном - цвет частиц и цвет символов может совпадать, а в другом - они могут быть только противоположны друг другу.

5.2. СВОЙСТВА ЧАСТИЦ ТРИАДНОГО СЕМЕЙСТВА

На рисунке 28 представлено уже триадное монадное семейство.

Рис. 28

Из рисунка видно, что это семейство отличается от дуадного тем, что для цветных частиц, при их последовательном синтезе по три, всегда оказывается справедливым принцип, что из трех частиц две будут одноцветными.

То же самое можно сказать и о символах частиц (рисунок справа). При последовательном обходе всегда выполняется условие компоновки - из трех частиц две будут одноименными, но разноцветными. На рисунке показано, что в данном монадном семействе принято комплексирование частиц, при котором каждая вершина представляет собой комбинацию -цвет частицы и цвет символа являются противоположными друг другу. Если мы примем другую "доктрину", то цвет вершины гексады и цвет ее символа (имя) будут совпадать.

Таким образом, и в случае триадных монадных семейств мы видим, что имеет место двойственность структуры монадных семейств.

Подобная двойственность компоновки дуадных и триадных семейств может иметь на практике далеко идущие последствия-частицы могут иметь прямо противоположные свойства. Так, например, если предположить, что такие частицы могут порождать некое "монадное поле", то в этом поле "разнозарядовые" частицы могут соответственно или притягиваться, или отталкиваться друг от друга, в то время как частиц с одинаковым знаком заряда будут соответственно отталкиваться или притягиваться друг к другу.

Дополнительную информацию о свойствах триадных семейств дает следующий рисунок.

Из этого рисунка видно, что цвета радуги принадлежат триадному семейству. И в этом семействе десять вершин. На рисунке справа показан крест, материализующий и дематериализующий цвета радуги. Из этого рисунка видно, что в центре ТРИАДНОГО КУБА не находится чисто белый и чисто черный цвета. В одном полюсе монады присутствует "фиолетовое смещение", а в другом -"красное смещение" ВЕЛИКОГО ПРЕДЕЛА монады "черное-белое".

6. О ЗАРЯДАХ МОНАДНЫХ ЧАСТИЦ

Выше, описывая свойства монадных кварков, мы пришли к выводу, что они могут иметь дробные заряды. Обозначим монадные кварки символами,

В этом случае, связывая с монадными кварками дробные заряды

s= -1/3, d= -1/3, u =2/3

мы получим

Рис. 29

Придавая монадным кваркам тот или иной физический смысл, мы будем получать ту или иную физическую интерпретацию их свойств. На вышеприведенном рисунке монадные кварки отождествлены с физическими кварками. Если теперь отождествить эти кварки с экспоненциальными, то мы получим, например, следующий набор экспоненциальных кварков

Из этих кварков можно построить все семейства экспоненциальных частиц, учитывая, что обход совершенной монадной формы для, например, двойственной пары , порождающей триплетное семейство будет происходить по схеме, изображенной на рис. 19. Подставляя полученные значения кварков в ту или иную экспоненциальную частицу триплетного семейства, мы получим соответствующую этой частице экспоненциальную функцию (истинно нейтральную, нейтральную, заряженные). Аналогично можно получить математическое описание триплетного семейства экспоненциальных античастиц.

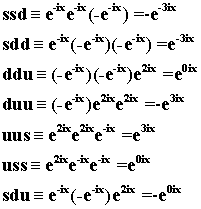Из полученного набора заряженных экспоненциальных частиц видно, что заряженные частицы характеризуются триадой экспоненциальных базисных функций, имеющих противоположную спиральность.

Экспоненциальные частицы непосредственно отражают смысл механизмов перенормировки кварков с базисными экспоненциальными функциями .

Так , мы будем иметь

для триады

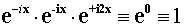для антитриады

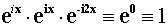Полученные из экспоненциальных кварков частицы также свидетельствуют, что в процессе эволюции экспоненциальной монады, частицы периодически перенормировываются. Более того, на определенном этапе эволюции экспоненциальная функция меняет свою спиральность.

Очевидно, что выбирая в качестве исходного набора другие наборы кварков, мы придем к аналогичному результату. Следовательно, ось вращения монадного кристалла всегда будет обладать нейтральным зарядом, а частицы будут всегда триплетными. Кроме того, они будут всегда разноименными и одноцветными (белыми или черными). Во "вращающемся" монадном кристалле, в соответствии с законами симметрии должна существовать и другая нейтральная "перекладина", которая должна уравновешивать положительные и отрицательные заряды в монадном кристалле.

Из этих выражений видно, что нейтральная монадная частица, интегрируя монадные кварки, осуществляет их перенормировку в новую частицу с целочисленным зарядом. Метод обратного пересчета приводит к виртуальному представлению о дробных зарядах.

Теперь, связывая с каждой экспоненциальной функцией понятие монадный спин, характеризующий ее ориентацию в пространстве (спин), мы получим возможность описать обход по кресту с использованием базисных экспоненциальных функций для монады "".

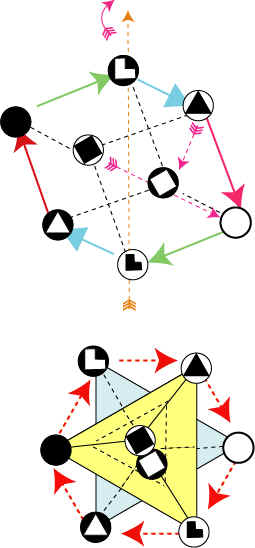Рис. 30

Последний рисунок характеризует очень важное свойство базисных экспоненциальных функций. Этот рисунок иллюстрирует проекции спина базисных функций на плоскость (направление и сдвиг фаз). Такие проекции единичных базисных функций на плоскость гексады получается в результате вращения куб (звездного тетраэдра вокруг оси симметрии, порождаемой двойственной парой "". Так, из рисунка видно, что проекции спина сдвинуты друг относительно друга на угол 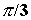. В результате проекция спина при замкнутом цикле эволюции двойственной пары совмещается с исходной через угол . В монадной форме при каждом переходе к новой вершине происходит поворот на угол . Поэтому возврат в исходное состояние происходит только после поворота на угол .

7. О МОНАДНЫХ МИРАХ И АНТИМИРАХ

Рассмотренные выше свойства монадных семейств (дуадных и триадных)

позволяют сделать определенные выводы и о взаимоотношениях частиц ("кварков"), порождающиех те или иные монадные семейства.

Рассмотрим взаимоотношения частиц и античастиц в мире дуадных семейств.

Из рисунков 13-21 видно, что каждая частица в дуадном семействе представляет собой единство "мира" и антимира". В дуадной гексаде частицы формируются за счет взаимодействия между собой кварковой триады и антитриады.

В триадных же семействах все частицы формируются из одноименных триад. Из рисунков 22-28 видно, что триадной гексаде все одноименные вершины триад стоят рядом, характеризуя единство. Поэтому в триадных семействах "мир" и "антимир" характеризуется уже не на триадном уровне (триада-антитриада), а на гексадном уровне (гексада-антигексада).

Другими словами, с повышением уровня иерархии монадных семейств "мир" и "антимир" все более и более отделяются друг от друга.

Однако различие между "мирами" и "антимирами" дуадными и триадными является существенным. Оно проявляется уже в свойствах исходных монад.

В дуадных семействах сама монада является дуадной (антагонистической).

В триадной монаде такого антагонизма нет. Здесь противоположности ("мир" и "антимир") являются уже взаимодополнительными.

РЕЗЮМЕ

1. Рассмотренные выше правила порождения монадных частиц из монадных кварков позволяют сделать вывод о том, что существуют всего только два типа монадных семейств -дуадные и триплетные семейства. Других семейств в природе не существует.

2. Анализ свойств монадных кварков позволил определить свойства некоторых специальных классов монадных семейств (экспоненциальные, семейство цветов радуги, музыкальной гаммы, элементарных частиц), имеющих общие свойства.

3. Рассмотренные правила порождения монадных частиц (и семейств) имеют чрезвычайно важное значение для всех без исключения отраслей наук, т.к. позволят осуществить научные прорывы во многих сферах знания. В природе нет других принципов классификации монадных частиц и их семейств, нет других правил их порождения. Эти свойства и правила будут являться едиными для любой Периодической системы, независимо от ее природы. Поэтому эти принципы и правила могут быть использованы в самых разных научных сферах знаний. Например:

в физике элементарных частиц эти принципы и правила помогут уточнить классификации семейств элементарных частиц,
в соционике - для обоснования единой классификации типов личностей человека, в частности, в настоящее время в соционике рассматриваются только дуадные типы, в то время как рассмотренные выше свойства монадных семейств позволяют применить к типам личностей и триплетный подход.
в генетике эти принципы помогут более глубоко проникнуть в тайны генетического кода, в тайны двойных дуплетных и триплетных цепочек,
в психологии рассмотренные принципы и методы порождения частиц и семейств из монадных кварков позволит понять дискретную природу психических состояний, дискретную природу сознания, эволюционые принципы и правила их порождения,
Не будут исключением из общего правила и другие важнейшие науки, такие, как социология, экономика, экология, духовные науки и др.

4.Рассмотренные принципы и правила порождения монадных семейств и частиц непосредственно характеризуют суть и сущность проявления Единого Универсального Закона эволюции живой и неживой материи применительно к любой системе, независимо от ее природы, включая законы эволюции Сознания, Разума и Высшего разума, демонстрируя единство Материи и Духа.

5. Рассмотренные выше принципы и правила порождения монадных семейств и свойства их частиц, позволили обосновать ряд Периодических законов эволюции систем различной природы с позиций Единого Периодического закона, единого научного подхода к интеграции научных знаний.

e-mail:

С благодарностью приму все ваши замечания, предложения, с признательностью отвечу на ваши вопросы

Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать о всех замеченных ошибках, некорректных формулировках.

Книги "Основы милогии", "Милогия" могут быть высланы в Ваш адрес наложенным платежом,

Карта сайта

rss

Карта