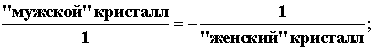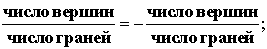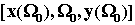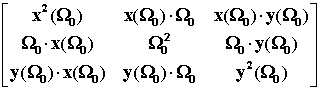О ВЫСШИХ ИЗМЕРЕНИЯХ
ЧАСТЬ
II.
4.
СОБСТВЕННЫЕ ПРОСТРАНСТВА И ТОЧКИ БИФУРКАЦИИ
О точках бифуркации на
страницах сайта упоминается на многих страницах сайта (О
синергетике,
Потоки ЯН-Инь, и др.). Но там мы рассматривали свойства точек
бифуркации применительно к Кубу Закона. Здесь мы попытаемся
дать дополнительную информацию.
Многообразие кристаллов
порождает и многообразие эволюционных потоков, циркулирующих в таких
кристаллах. Но все они рождаются по образу и подобию.
Женские кристаллы
 рис. 12
Нетрудно увидеть, что все эти кристаллы
порождаются в конечном итоге треугольниками
(òðèàäàìè, òðèãðàììàìè). Ïðèâåäåííûå âûøå ôîðìû êðèñòàëëîâ îòðàæàþò
ñâîéñòâà ïðîñòåéøèõ êðèñòàëëîâ ñîáñòâåííûõ ïðîñòðàíñòâ. Íî ñóùåñòâóåò åùå
ìèð çâåçäíûõ êðèñòàëëîâ. È âñå îíè õàðàêòåðèçóþòñÿ òðèåäèíñòâîì.
Мужские кристаллы
рис. 12
Нетрудно увидеть, что все эти кристаллы
порождаются в конечном итоге треугольниками
(òðèàäàìè, òðèãðàììàìè). Ïðèâåäåííûå âûøå ôîðìû êðèñòàëëîâ îòðàæàþò
ñâîéñòâà ïðîñòåéøèõ êðèñòàëëîâ ñîáñòâåííûõ ïðîñòðàíñòâ. Íî ñóùåñòâóåò åùå
ìèð çâåçäíûõ êðèñòàëëîâ. È âñå îíè õàðàêòåðèçóþòñÿ òðèåäèíñòâîì.
Мужские кристаллы
 рис. 13
Из приведенных
рисунков мужских и женских кристаллов видно, что они характеризуются
отношением вида
рис. 13
Из приведенных
рисунков мужских и женских кристаллов видно, что они характеризуются
отношением вида
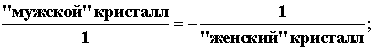 Поскольку каждый
такой кристалл характеризуется отношением числа вершин к числу граней, то мы
можем записать равновесное тожд6ество между "мужскими" и "женскими"
кристаллами"
Поскольку каждый
такой кристалл характеризуется отношением числа вершин к числу граней, то мы
можем записать равновесное тожд6ество между "мужскими" и "женскими"
кристаллами"
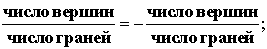 Подобные отношения существуют и между двумя "соседними" Платоновыми
телами. Здесь отношениями "мужское-женское" характеризуются пары
"октаэдр-куб", "икосаэдр-додекаэдр".
А поскольку каждый кристалл из этих пар
может быть женским, или мужским (без "шипов", с "шипами"), т.е.
характеризоваться как "внешнее" (мужское) и "внутреннее" (женское"), то
невольно вспоминаются высказывание Иисуса Христа о Царствии небесном
"Когда вы сделаете внутренне как внешнее,
женское как мужское, мужское как женское, тогда вы войдете в Царствие...".
Таким образом, это высказывание отражает глубинный смысл эволюции не только
рода людского, но и мира кристаллов.
На данных
рисунках приведены далеко не все виды кристаллов. Но все эти кристаллы
свидетельствуют о том, что все измерения в них являются строго
упорядоченными и что все кристаллы формируются по образу и подобию, по Единому
Закону эволюции двойственного отношения. Единый Закон, порождая Пирамиду Силы
и соответствующие хроматические гаммы не может порождать уродливые
аккорды. Все аккорды, порождаемые Единым законом гармоничны. Поэтому в любых
кристаллах существует собственная гармония, порождаемая тем или иным
"Творцом", находящимся на том или ином уровне иерархии Творцов и потому любой
ЗАМЫСЕЛ такого Творца уже изначально несет в себе свойства порождаемых им
измерений кристаллов. И все эти "Творцы" обладают общими свойствами.
5. О ЗАМКНУТОСТИ ИЗМЕРЕНИЙ
Универсальный закон эволюции
материи свидетельствует о замкнутости пространств. Закономерность ограниченности
и замкнутости пространств является следствием этого Универсального закона
эволюции двойственного отношения.
Из рисунков, приводимых выше, видно, что
внешний контур многоугольников, характеризующих двумерную проекцию
пространственных монадных кристаллов оказываются замкнутыми.
На
рис. 14 изображено три проекции на плоскость 2-х мерного, 3-х мерного, 4-х
мерного и 6-ти мерного пространств.
Подобные отношения существуют и между двумя "соседними" Платоновыми
телами. Здесь отношениями "мужское-женское" характеризуются пары
"октаэдр-куб", "икосаэдр-додекаэдр".
А поскольку каждый кристалл из этих пар
может быть женским, или мужским (без "шипов", с "шипами"), т.е.
характеризоваться как "внешнее" (мужское) и "внутреннее" (женское"), то
невольно вспоминаются высказывание Иисуса Христа о Царствии небесном
"Когда вы сделаете внутренне как внешнее,
женское как мужское, мужское как женское, тогда вы войдете в Царствие...".
Таким образом, это высказывание отражает глубинный смысл эволюции не только
рода людского, но и мира кристаллов.
На данных
рисунках приведены далеко не все виды кристаллов. Но все эти кристаллы
свидетельствуют о том, что все измерения в них являются строго
упорядоченными и что все кристаллы формируются по образу и подобию, по Единому
Закону эволюции двойственного отношения. Единый Закон, порождая Пирамиду Силы
и соответствующие хроматические гаммы не может порождать уродливые
аккорды. Все аккорды, порождаемые Единым законом гармоничны. Поэтому в любых
кристаллах существует собственная гармония, порождаемая тем или иным
"Творцом", находящимся на том или ином уровне иерархии Творцов и потому любой
ЗАМЫСЕЛ такого Творца уже изначально несет в себе свойства порождаемых им
измерений кристаллов. И все эти "Творцы" обладают общими свойствами.
5. О ЗАМКНУТОСТИ ИЗМЕРЕНИЙ
Универсальный закон эволюции
материи свидетельствует о замкнутости пространств. Закономерность ограниченности
и замкнутости пространств является следствием этого Универсального закона
эволюции двойственного отношения.
Из рисунков, приводимых выше, видно, что
внешний контур многоугольников, характеризующих двумерную проекцию
пространственных монадных кристаллов оказываются замкнутыми.
На
рис. 14 изображено три проекции на плоскость 2-х мерного, 3-х мерного, 4-х
мерного и 6-ти мерного пространств.

Рис.
14
Вектор устремлений в
многоугольниках, отражающих 2-х мерную проекцию более высших измерений
в данном случае равен нулю, т.е. система уравновешена.
Она свернута в
нуль-мерный вектор -точку (скаляр). Но
этот скаляр будет помнить всю свою историю. Для этого надо запомнить только
его "спин", по которому можно однозначно возродить прошлое. т.е. осуществить
разворачивание нуль-вектора в многомерный вектор (Генная
память).
Если
теперь мы будем увеличивать число измерений до бесконечности, то
проекции базисных векторов многомерного пространства образуют замкнутый
многоугольник,
который трансформируется в окружность. Но эта окружность будет иметь
собственный
вектор устремлений
- характеризующий крутящий момент
сформированной "силовой линии поля".
Возникает как бы естественное
обоснование
"вращающейся Вселенной",
образование системы "силовых линий Вселенных", формирование Единого
Самосогласованного Поля.
Отметим, что среди
всех измерений особое место занимает монада -двойственное отношение,
которое замыкается само на себя "без вращения".
Она нейтральна к вращениям.
Она ось симметрии вращений.
Она не вращается,
но все вращается вокруг нее.
Любое замкнутое пространство является собственным пространством (Теория
иерархии). Поэтому любое собственное пространство, в
соответствии с законом диалектики о переходе количества в качество,
может характеризоваться как процесс нормировки замкнутого пространства в
единичное (Информация).
В
результате свертки замкнутого
m-мерного пространства
мы
получаем собственное пространство, свернутое в (вектор-бит)
со внутренней размерностью собственного (m-1)
пространства, т.е.
внутренняя размерность собственного пространства оказывается на единицу меньше
замкнутого пространства, составленного из собственных векторов устремлений
этого пространства.
Таким образом,
можно сказать, что из вершины
вектора-бита
любого собственного пространства
можно обозревать все собственное
пространство. Этот вектор - бит по своему смыслу определяет единичный
вектор устремления замкнутого пространства.
Если
отождествить этот вектор-бит с монадой собственного пространства, то один
полюс монады будет содержать произведение собственного значения (С)
на единичный вектор-бит (1),
т.е.
С*1, в
то время как другой полюс монады замкнутого
пространства будет содержать величину обратную, т.е. будет характеризоваться
значением
1/С.
При этом перемножение полюсов всегда приводит к результату
(С*1)*(
1/С)
=1, т.е. порождает
бит в "чистом" виде.
Умножая данный бит, или любое число бит на соответствующее значение того
или иного полюса монады собственного пространства, мы тем самым будем
осуществлять инвариантный переход к низшему, или высшему измерению
соответствующего (текущего) собственного пространства. При этом, в случае,
если умножаемое число не будет равно единице, мы получим инвариантные
переходы из одного собственного пространства в другое, с учетом
абсолютных собственных значений для конкретно рассматриваемого собственного
пространства.
Ñëåäóåò îòìåòèòü åùå îäíî âàæíåéøåå ñâîéñòâî âûñøèõ èçìåðåíèé.
Êàæäîå ïðîñòðàíñòâî âûñøèõ èçìåðåíèé ìîæåò íåñòè ÿíñêèé (ìóæñêîé) èëè
èíüñêèé (æåíñêèé) àñïåêòû.
Ïðèâåäåííûå âûøå ðèñóíêè êðèñòàëëîâ (ðèñ. 12 è 13) â ÿâíîì âèäå
îòðàæàþò ýòè àñïåêòû. Êðèñòàëëû, íà ðèñ. 12 îòðàæàþò èíüñêèé àñïåêò,
èáî òî÷êè ñáîðêè-ðàçáîðêè ó íèõ ðàçìåùàþòñÿ â öåíòðå êðèñòàëëà.
Îíè îòðàæàþò â ñåáå ãëîáàëüíóþ òî÷êó ñáîðêè-ðàçáîðêè ñîîòâåòñòâóþùåãî
ïðîñòðàíñòâà.
Êðèñòàëëû ðèñ. 12 îòðàæàþò â ñåáå ÿíñêèé àñïåêò. Çäåñü êàæäàÿ òî÷êà ñáîðêè
-ðàçáîðêè ðàçìåùàåòñÿ âíå ìàòåðèíñêîãî êðèñòàëëà è âñå îíè îòäåëåíû
äðóã îò äðóãà. Îíè íåñóò â ñåáå àñïåêò ÷ëåíåíèÿ öåëîãî íà ÷àñòè,
ïîâûøàÿ "ýíòðîïèþ" ñîáñòâåííîãî ïðîñòðàíñòâà êðèñòàëëà.
Ñâîéñòâà ÿíñêèõ è èíüñêèõ êðèñòàëëîâ ïðîÿâëÿþòñÿ íà âñåõ óðîâíÿõ ìèðîçäàíèÿ.
"×åðíûå äûðû" îòðàæàþò â ñåáå ñâîéñòâà èíüñêèõ ãèïåðïðîñòðàíñòâ, â òî âðåìÿ
êàê "áåëûå äûðû" íåñóò â ñåáå ÿíñêèé àñïåêò ãèïåðïðîñòðàíñòâ, èáî îíè
èçëó÷àþò ýíåðãèþ.
Ýòè ñâîéñòâà êðèñòàëëîâ ìèðîçäàíèÿ îòðàæàòü èëè ÿíñêèé èëè èíüñêèé àñïåêòû
ÿâëÿþòñÿ íàñòîëüêî âñåîáùèìè, ÷òî íå ó÷èòûâàòü èõ ïðîñòî íåâîçìîæíî, õîòÿ
ñåãîäíÿ ñîâðåìåííàÿ íàóêà òîëüêî è çàíèìàåòñÿ òåì, ÷òî îíà íå õî÷åò çàìå÷àòü
î÷åâèäíûå èñòèíû.
È çäåñü èìååò ìåñòî ïîëíàÿ àíàëîãèÿ ñ óðîâíåì ìûøëåíèÿ è ñîçíàíèÿ ëþäåé. Íà
ñòðàíèöå "Íàóêà è Âåðà" áûëè îáîñíîâàíû ôèëüòðû
ñîçíàíèÿ, êîòîðûå ïî îáðàçó è ïîäîáèþ ôîðìèðóþò áåññîçíàòåëüíîå ìûøëåíèå
ëþäåé è êîëëåêòèâíî-áåññîçíàòåëüíîå ìûøëåíèå îáùåñòâà.
Áåññîçíàòåëüíîñòü ïðîÿâëÿåòñÿ âî âñå áîëåå âîçðàñòàþùåé ýíòðîïèè "õîëîäíîãî
óìà" êàæäîãî èíäèâèäóóìà, à ïîñêîëüêó Êîëëåêòèâíûé ðàçóì ôîðìèðóåòñÿ èç
áåñêîíå÷íî îòäàëÿþùèõñÿ äðóã îò äðóãà áåñêîíå÷íî èíòåëëåêòóàëüíûõ ðàçóìîâ,
òî è Êîëëåêòèâíûé ðàçóì âñå áîëåå è áîëåå òðàíñôîðìèðóåòñÿ â
áåñêîíå÷íî "èíòåëëåêòóàëüíî-äåìîêðàòè÷åñêèé", íî áåññîçíàòåëüíûé ðàçóì ñî
âñå âîçðàñòàþùåé ýíòðîïèåé.
Õîòåëîñü áû íàäåÿòüñÿ, ÷òî ëþäè îñîçíàþò ñàìóþ ñîêðîâåííóþ òàéíó
Åäèíîãî Çàêîíà ýâîëþöèè äâîéñòâåííîãî îòíîøåíèÿ, íåçàâèñèìî îò åãî
âåùåñòâåííîé èëè ïîëåâîé ïðèðîäû, îñîçíàþò, ÷òî ïî ýòîìó çàêîíó ôîðìèðóþòñÿ
ñîáñòâåííûå ïðîñòðàíñòâà âñåõ âûñøèõ èçìåðåíèé, ÷òî âñå ýòè ïðîñòðàíñòâà
âçàèìîñâÿçàíû ìåæäó ñîáîé.
6.
ÃÈÏÅÐÌÀÒÐÈÖÀ ÊÓÁÀ
Ñîáñòâåííûå ïðîñòðàíñòâà, ôîðìèðóåìûå èç îäíîãî è òîãî æå Çàìûñëà Òâîðåíèÿ (íóëü-ìåðíîãî
ïðîñòðàíñòâà-×èñëà) ïîðîæäàþò ñîâåðøåííûå ãèïåðêðèñòàëëû ñîáñòâåííûõ
ãèïåðïðîñòðàíñòâ ãèïåð Ïëàòîíîâûõ òåë (ãèïåðòåòðàýäðû, ãèïåðîêòàýäðû,
ãòïåðêóáû, ãèïåðèêîñàýäðû, ãèïåðäîðäåêàýäðû).
 êîíå÷íîì èòîãå âñå ãèïåðïðîñòðàíñòâà îòðàæàþòñÿ â ñâîéñòâàõ
Ïëàòîíîâûõ òåë è ôîðìèðóþòñÿ èç òðåóãîëüíèêîâ (òðèàä, òðèãðàìì). Èåðàðõèÿ
ñîáñòâåííûõ ïðîñòðàíñòâ, Åäèíûé çàêîí ýâîëþöèè ìîíàäû íåèçáåæíî
ïîðîæäàþò çàìêíóòîñòü ñîáñòâåííûõ ïðîñòðàíñòâ, ïðè êîòîðîé íà íîâîé óðîâíå
èåðàðõèè ëþáîå ñîáñòâåííîå ïðîñòðàíñòâî íà÷èíàåò ôîðìèðîâàòüñÿ ïî
îáðàçó è ïîäîáèþ, ïîðîæäàÿ òàêèì îáðàçîì ñïåöèôè÷åñêèå ñîáñòâåííûå
ãèïåðïðîñòðàíñòâà.
Ðàññìîòðèì ñëåäóþùóþ áàçèñíóþ òðèàäó
 ðèñ. 15
Èç
ýòîé òðèàäû, ïî îáðàçó è ïîäîáèþ ñîçäàþòñÿ âñå ñîáñòâåííûå ïðîñòðàíñòâà
Ïëàòîíîâûõ òåë.
Ýòà òðèàäà ÿâëÿåòñÿ ñèñòåìîîáðàçóþùåé âñåõ
ñîáñòâåííûõ ïðîñòðàíñòâ Ìèðîçäàíèÿ.
 ýòîé òðèàäå ñèìâîë
W0
îçíà÷àåò
Çàìûñåë Òâîðåíèÿ.
Ýòà òðèàäà ôîðìèðóåò ñòðîêó ìàòðèöû
ðèñ. 15
Èç
ýòîé òðèàäû, ïî îáðàçó è ïîäîáèþ ñîçäàþòñÿ âñå ñîáñòâåííûå ïðîñòðàíñòâà
Ïëàòîíîâûõ òåë.
Ýòà òðèàäà ÿâëÿåòñÿ ñèñòåìîîáðàçóþùåé âñåõ
ñîáñòâåííûõ ïðîñòðàíñòâ Ìèðîçäàíèÿ.
 ýòîé òðèàäå ñèìâîë
W0
îçíà÷àåò
Çàìûñåë Òâîðåíèÿ.
Ýòà òðèàäà ôîðìèðóåò ñòðîêó ìàòðèöû
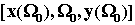 Âåëèêèé ïðåäåë ýòîé ìàòðèöû-ñòðîêè
ðàâåí 3 ([1,3,2]),ò.å.
W0
=3.
Óìíîæàÿ ýòó ñòðîêó íà
ñîîòâåòñòâóþùèé ñòîëáåö, ìû ïîëó÷èì ìàòðèöó ðàçìåðíîñòüþ 3õ3
Âåëèêèé ïðåäåë ýòîé ìàòðèöû-ñòðîêè
ðàâåí 3 ([1,3,2]),ò.å.
W0
=3.
Óìíîæàÿ ýòó ñòðîêó íà
ñîîòâåòñòâóþùèé ñòîëáåö, ìû ïîëó÷èì ìàòðèöó ðàçìåðíîñòüþ 3õ3
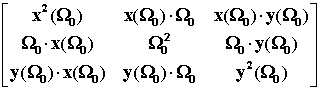 Ýòà
ìàòðèöà ÿâëÿåòñÿ óæå ïðîåêöèåé êóáà íà ïëîñêîñòü. Â ýòîé ìàòðèöå íîâûé
Âåëèêèé Ïðåäåë ðàâåí (W0
)2=3õ3=9. Ýòà ìàòðèöà îáëàäàåò
öåëûì ðÿäîì çàìå÷àòåëüíûõ ñâîéñòâ
Ýòà
ìàòðèöà ÿâëÿåòñÿ óæå ïðîåêöèåé êóáà íà ïëîñêîñòü. Â ýòîé ìàòðèöå íîâûé
Âåëèêèé Ïðåäåë ðàâåí (W0
)2=3õ3=9. Ýòà ìàòðèöà îáëàäàåò
öåëûì ðÿäîì çàìå÷àòåëüíûõ ñâîéñòâ
 Ýòà ñèñòåìà óðàâíåíèé îïðåäåëÿåò
ïîñëåäîâàòåëüíîñòü ôîðìèðîâàíèÿ âåðøèí êóáà. Îäíîâðåìåííî îíà îïðåäåëÿåò
÷åòûðå áàçèñíûõ "ñòèõèè", êîòîðûå èãðàþò ðîëü ÄÍÊ, èç êîòîðûõ ôîðìèðóåòñÿ
ìàòðèöà êóáà, à çàòåì è ìàòðèöû âûñøèõ èçìåðåíèé.
Ïîëó÷åííûå òîæäåñòâà èìåþò ïðîñòîé
ãåîìåòðè÷åñêèé ñìûñë.
Ýòà ñèñòåìà óðàâíåíèé îïðåäåëÿåò
ïîñëåäîâàòåëüíîñòü ôîðìèðîâàíèÿ âåðøèí êóáà. Îäíîâðåìåííî îíà îïðåäåëÿåò
÷åòûðå áàçèñíûõ "ñòèõèè", êîòîðûå èãðàþò ðîëü ÄÍÊ, èç êîòîðûõ ôîðìèðóåòñÿ
ìàòðèöà êóáà, à çàòåì è ìàòðèöû âûñøèõ èçìåðåíèé.
Ïîëó÷åííûå òîæäåñòâà èìåþò ïðîñòîé
ãåîìåòðè÷åñêèé ñìûñë.
 ðèñ. 16
Âèäèòå, âñå ÷åòûðå áàçèñíûõ "ñòèõèè" îêàçûâàþòñÿ âçàèìíî ñáàëàíñèðîâàííûìè è
íîðìèðîâàíû ê åäèíîìó ×èñëó (9)-Âåëèêîìó ïðåäåëó Êóáà. Ýòî òî÷êà ñáîðêè è
ðàçáîðêè ñîîòâåòñòâóþùåãî ñîáñòâåííîãî ïðîñòðàíñòâà. èìåþùåãî ñîáñòâåííûé
Çàìûñåë Òâîðåíèÿ.
Íî íà ñòðàíèöå "Êîíöåïöèè"
ìû óæå ïîêàçûâàëè, ÷òî (W0
)2=W1
è ïîòîìó ìû ìîæåò ñòðîèòü, ïî îáðàçó è ïîäîáèþ íîâîå
ãèïåðïðîñòðàíñòâî.
Ïîëîæèì, ÷òî áàçèñíàÿ ìàòðèöà áóäåò èìåòü
ðàçìåðíîñòü 2õ2
ðèñ. 16
Âèäèòå, âñå ÷åòûðå áàçèñíûõ "ñòèõèè" îêàçûâàþòñÿ âçàèìíî ñáàëàíñèðîâàííûìè è
íîðìèðîâàíû ê åäèíîìó ×èñëó (9)-Âåëèêîìó ïðåäåëó Êóáà. Ýòî òî÷êà ñáîðêè è
ðàçáîðêè ñîîòâåòñòâóþùåãî ñîáñòâåííîãî ïðîñòðàíñòâà. èìåþùåãî ñîáñòâåííûé
Çàìûñåë Òâîðåíèÿ.
Íî íà ñòðàíèöå "Êîíöåïöèè"
ìû óæå ïîêàçûâàëè, ÷òî (W0
)2=W1
è ïîòîìó ìû ìîæåò ñòðîèòü, ïî îáðàçó è ïîäîáèþ íîâîå
ãèïåðïðîñòðàíñòâî.
Ïîëîæèì, ÷òî áàçèñíàÿ ìàòðèöà áóäåò èìåòü
ðàçìåðíîñòü 2õ2
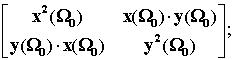 Â ýòîé ìàòðèöå
â ÿâíîì âèäå îòñóòñòâóåò òî÷êà ñáîðêè. Îäíàêî ýòà òî÷êà èìååòñÿ, íî îíà
íàõîäèòñÿ âíå äàííîé ìàòðèöû, îòðàæàÿñü â ñâîéñòâàõ äàííûõ ÷åòûðåõ îñíîâàíèé
("ñòèõèé").
Îíà îòðàæàåòñÿ â âåñàõ
ìîíàäû
 ýòîé ìàòðèöå
â ÿâíîì âèäå îòñóòñòâóåò òî÷êà ñáîðêè. Îäíàêî ýòà òî÷êà èìååòñÿ, íî îíà
íàõîäèòñÿ âíå äàííîé ìàòðèöû, îòðàæàÿñü â ñâîéñòâàõ äàííûõ ÷åòûðåõ îñíîâàíèé
("ñòèõèé").
Îíà îòðàæàåòñÿ â âåñàõ
ìîíàäû
 ðèñ. 17
Èç ýòîãî
ðèñóíêà íåïîñðåäñòâåííî âèäíî, ÷òî ÷åòûðå áàçèñíûõ îñíîâàíèÿ ("ñòèõèè")
äâîéñòâåííîãî îòíîøåíèÿ ôîðìèðóþò ïÿòóþ "ñòèõèþ", îòíîñèòåëüíî êîòîðîé
ïðîèçâîäèòñÿ "áàëàíñèðîâêà" âåñîâ ìîíàäû. Ýòà ïÿòàÿ "ñòèõèÿ"
ðàñïîëàãàåòñÿ íà ïåðåñå÷åíèè äâóõ ïåðåêëàäèí âåñîâ.
Ïîýòîìó ìû ìîæåò çàïèñàòü òåïåðü âçàèìîîòíîøåíèÿ ìåæäó
ýòèìè ïÿòüþ áàçèñíûìè îñíîâàíèÿìè âåñîâ.
ðèñ. 17
Èç ýòîãî
ðèñóíêà íåïîñðåäñòâåííî âèäíî, ÷òî ÷åòûðå áàçèñíûõ îñíîâàíèÿ ("ñòèõèè")
äâîéñòâåííîãî îòíîøåíèÿ ôîðìèðóþò ïÿòóþ "ñòèõèþ", îòíîñèòåëüíî êîòîðîé
ïðîèçâîäèòñÿ "áàëàíñèðîâêà" âåñîâ ìîíàäû. Ýòà ïÿòàÿ "ñòèõèÿ"
ðàñïîëàãàåòñÿ íà ïåðåñå÷åíèè äâóõ ïåðåêëàäèí âåñîâ.
Ïîýòîìó ìû ìîæåò çàïèñàòü òåïåðü âçàèìîîòíîøåíèÿ ìåæäó
ýòèìè ïÿòüþ áàçèñíûìè îñíîâàíèÿìè âåñîâ.
 Ýòè ÷èñëà îòðàæàþò ïîñëåäîâàòåëüíîñòü ôîðìèðîâàíèÿ âåðøèí òåòðàýäðà. Äâà
âçàèìîäîïîëíèòåëüíûõ òåòðàýäðà ôîðìèðóþò çâåçäíûé òåòðàýäð (èëè êóá, èáî ýòè
êðèñòàëëû ÿâëÿþòñÿ âçàèìîäîïîëíèòåëüíûìè).
Íî, ñ äðóãîé ñòîðîíû, êóá ôîðìèðóåòñÿ äâóìÿ 4-õ óãîëüíûìè ïèðàìèäàìè, ñ
îáùèì öåíòðîì. À êàê èçâåñòíî, â ýòîé ïèðàìèäå 5 âåðøèí.
Áàçèñíûå ÷åòûðå "ñòèõèè" (òåòðàýäð) ïîðîæäàþò 3-õ óãîëüíóþ ïèðàìèäó (òåòðàýäð).
Ýòî è åñòü òà ñàìàÿ ýëåìåíòàðíàÿ êëåòî÷íàÿ ìàòðèöà, íåñóùàÿ â ñåáå Çàìûñåë
Òâîðåíèÿ òîãî èëè èíîãî ÃèïåðÌèðîçäàíèÿ.
è ýòîò
òåòðàýäð, ïî îáðàçó è ïîäîáèþ, ìîæåò ïîðîæäàòü ãèïåðòåòðàýäð (ðèñ. 19).
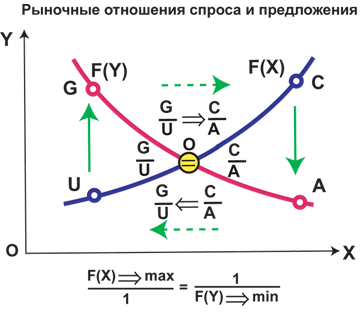
Ýòà áàçèñíàÿ ìàòðèöà óæå èçíà÷àëüíî îòðàæàåò â ñåáå âåñû ðûíî÷íûõ
âçàèìîîòíîøåíèé ìåæäó ÷åòûðüìÿ îñíîâàíèÿìè ("ñòèõèÿìè") äàííîé êëåòî÷íîé
ìàòðèöû, ò.å. äàííàÿ êëåòî÷íàÿ ìàòðèöà ñïîñîáíà òðàíñôîðìèðîâàòüñÿ â êðèñòàëë
âûñøåãî èçìåðåíèÿ - 4-õ óãîëüíîé ìàòðèöå.
Ýòî îçíà÷àåò, ÷òî äàííàÿ ìàòðèöà ìîæåò ñâîðà÷èâàòüñÿ â Çàìûñåë Òâîðåíèÿ è ìîæåò
ðàçâîðà÷èâàòüñÿ èç Çàìûñëà Òâîðåíèÿ â áàçèñíóþ ìàòðèöó ðàçìåðíîñòüþ 2õ2.
Ýòè ÷èñëà îòðàæàþò ïîñëåäîâàòåëüíîñòü ôîðìèðîâàíèÿ âåðøèí òåòðàýäðà. Äâà
âçàèìîäîïîëíèòåëüíûõ òåòðàýäðà ôîðìèðóþò çâåçäíûé òåòðàýäð (èëè êóá, èáî ýòè
êðèñòàëëû ÿâëÿþòñÿ âçàèìîäîïîëíèòåëüíûìè).
Íî, ñ äðóãîé ñòîðîíû, êóá ôîðìèðóåòñÿ äâóìÿ 4-õ óãîëüíûìè ïèðàìèäàìè, ñ
îáùèì öåíòðîì. À êàê èçâåñòíî, â ýòîé ïèðàìèäå 5 âåðøèí.
Áàçèñíûå ÷åòûðå "ñòèõèè" (òåòðàýäð) ïîðîæäàþò 3-õ óãîëüíóþ ïèðàìèäó (òåòðàýäð).
Ýòî è åñòü òà ñàìàÿ ýëåìåíòàðíàÿ êëåòî÷íàÿ ìàòðèöà, íåñóùàÿ â ñåáå Çàìûñåë
Òâîðåíèÿ òîãî èëè èíîãî ÃèïåðÌèðîçäàíèÿ.
è ýòîò
òåòðàýäð, ïî îáðàçó è ïîäîáèþ, ìîæåò ïîðîæäàòü ãèïåðòåòðàýäð (ðèñ. 19).
Ýòà áàçèñíàÿ ìàòðèöà óæå èçíà÷àëüíî îòðàæàåò â ñåáå âåñû ðûíî÷íûõ
âçàèìîîòíîøåíèé ìåæäó ÷åòûðüìÿ îñíîâàíèÿìè ("ñòèõèÿìè") äàííîé êëåòî÷íîé
ìàòðèöû, ò.å. äàííàÿ êëåòî÷íàÿ ìàòðèöà ñïîñîáíà òðàíñôîðìèðîâàòüñÿ â êðèñòàëë
âûñøåãî èçìåðåíèÿ - 4-õ óãîëüíîé ìàòðèöå.
Ýòî îçíà÷àåò, ÷òî äàííàÿ ìàòðèöà ìîæåò ñâîðà÷èâàòüñÿ â Çàìûñåë Òâîðåíèÿ è ìîæåò
ðàçâîðà÷èâàòüñÿ èç Çàìûñëà Òâîðåíèÿ â áàçèñíóþ ìàòðèöó ðàçìåðíîñòüþ 2õ2.
 ðèñ. 19
ðèñ. 19
 ðèñ.
20
Íåòðóäíî óâèäåòü, ÷òî ñôîðìèðîâàëàñü óæå 4-õ óãîëüíàÿ ãèïåðïèðàìèäà. Îíà
ñîäåðæèò 4 ñåêòîðà, â êàæäîì èç êîòîðûõ èìååòñÿ ñâîÿ áàçèñíàÿ ìàòðèöà,
ñîäåðæàùàÿ Çàìûñåë òâîðåíèÿ.
Íó ÷åì íå êëåòêè æèâîãî îðãàíèçìà, êàæäàÿ
èç êîòîðûõ ñîäåðæèò â ñåáå êîä ÄÍÊ?
Ïðè ýòîì âåðøèíû îêàçûâàþòñÿ ñãðóïïèðîâàííûìè â 4 òðèàäû, ñ îáùèì ÷èñëîì âåðøèí,
ðàâíûì 12.
Òåïåðü ïîÿâëÿåòñÿ âîçìîæíîñòü ôîðìèðîâàíèÿ ïðîñòðàíñòâà âûñøåãî èçìåðåíèÿ-êóáà è
ãèïåðêóáà. Ïîñêîëüêó îêòàýäð è êóá ÿâëÿþòñÿ âçàèìíûìè, òî, â ñîîòâåòñòâèè ñ
âåñàìè
ðèñ.
20
Íåòðóäíî óâèäåòü, ÷òî ñôîðìèðîâàëàñü óæå 4-õ óãîëüíàÿ ãèïåðïèðàìèäà. Îíà
ñîäåðæèò 4 ñåêòîðà, â êàæäîì èç êîòîðûõ èìååòñÿ ñâîÿ áàçèñíàÿ ìàòðèöà,
ñîäåðæàùàÿ Çàìûñåë òâîðåíèÿ.
Íó ÷åì íå êëåòêè æèâîãî îðãàíèçìà, êàæäàÿ
èç êîòîðûõ ñîäåðæèò â ñåáå êîä ÄÍÊ?
Ïðè ýòîì âåðøèíû îêàçûâàþòñÿ ñãðóïïèðîâàííûìè â 4 òðèàäû, ñ îáùèì ÷èñëîì âåðøèí,
ðàâíûì 12.
Òåïåðü ïîÿâëÿåòñÿ âîçìîæíîñòü ôîðìèðîâàíèÿ ïðîñòðàíñòâà âûñøåãî èçìåðåíèÿ-êóáà è
ãèïåðêóáà. Ïîñêîëüêó îêòàýäð è êóá ÿâëÿþòñÿ âçàèìíûìè, òî, â ñîîòâåòñòâèè ñ
âåñàìè
 ïðîèñõîäÿò èíâàðèàíòíûå òðàíñôîðìàöèè ìåæäó ýòèìè êðèñòàëëàìè.
Ìîæåò
ëè îêòàýäð ôîðìèðîâàòü ñîáñòâåííîå ãèïåðïðîñòðàíñòâî (ãèïåðîêòàýäð)?
Åñëè ìû íà ìåñòî êàæäîé âåðøèíû îêòàýäðà ïîìåñòèì îêòàýäð,
òî ìû ïîëó÷èì íåéòðàëüíûé ãèïåðîêòàýäð. Åãî íåéòðàëüíîñòü ïðîÿâëÿåòñÿ â òîì, ÷òî
ýòî áóäåò ïîèñòèíå çâåçäíûé êóá, ñîñòîÿùèé èç 6 îêòàýäðîâ, îñíîâàíèÿ
êîòîðûõ
ôîðìèðóþò êóá. Ïðè ýòîì 6 âåðøèí
ðàñïîëàãàþòñÿ â öåíòðå êóáà, à 6 -âíå êóáà.
Òàêèì îáðàçîì, Âåëèêèé ïðåäåë çâåçäíîãî ãèïåðêóáà ñîäåðæèò â ñåáå 6 âåðøèí.
Ñòîëüêî æå âåðøèí ñîäåðæèò è Âåëèêèé ïðåäåë êóáà.
Äàëåå, íåòðóäíî óâèäåòü, ÷òî 4 ñåêòîðà ýòîé ìàòðèöû ñîäåðæàò 64 ýëåìåíòà,
ñãðóïïèðîâàííûõ â ìàòðèöó ðàçìåðíîñòè 8õ8. Ðîâíî ñòîëüêî æå, ñêîëüêî òðèãðàìì
ñîäåðæèòñÿ â ìàòðèöå È-Öçèí. À ýòî óæå ãèïåðêóá.
Ðàññìîòðèì ãåîìåòðè÷åñêèé ñìûñë ïðîñòðàíñòâà ãèïåðêóáà.
Ðàçâåðíåì êóá â ñòðîêó òðèãðàìì è óìíîæèì íà ñîîòâåòñòâóþùèé ñòîëáåö
òðèãðàìì. â ðåçóëüòàòå ìû ìû ïîëó÷èì ìàòðèöó È-Öçèí, ðàçìåðíîñòüþ 8õ8, â êîòîðîé
ñ êàæäîé òðèãðàììîé ñâÿçàíà åå ãåîìåòðè÷åñêàÿ èíòåðïðåòàöèÿ, îòðàæàþùàÿ åå
îðèåíòàöèþ â ïðîñòðàíñòâå êóáà.
ïðîèñõîäÿò èíâàðèàíòíûå òðàíñôîðìàöèè ìåæäó ýòèìè êðèñòàëëàìè.
Ìîæåò
ëè îêòàýäð ôîðìèðîâàòü ñîáñòâåííîå ãèïåðïðîñòðàíñòâî (ãèïåðîêòàýäð)?
Åñëè ìû íà ìåñòî êàæäîé âåðøèíû îêòàýäðà ïîìåñòèì îêòàýäð,
òî ìû ïîëó÷èì íåéòðàëüíûé ãèïåðîêòàýäð. Åãî íåéòðàëüíîñòü ïðîÿâëÿåòñÿ â òîì, ÷òî
ýòî áóäåò ïîèñòèíå çâåçäíûé êóá, ñîñòîÿùèé èç 6 îêòàýäðîâ, îñíîâàíèÿ
êîòîðûõ
ôîðìèðóþò êóá. Ïðè ýòîì 6 âåðøèí
ðàñïîëàãàþòñÿ â öåíòðå êóáà, à 6 -âíå êóáà.
Òàêèì îáðàçîì, Âåëèêèé ïðåäåë çâåçäíîãî ãèïåðêóáà ñîäåðæèò â ñåáå 6 âåðøèí.
Ñòîëüêî æå âåðøèí ñîäåðæèò è Âåëèêèé ïðåäåë êóáà.
Äàëåå, íåòðóäíî óâèäåòü, ÷òî 4 ñåêòîðà ýòîé ìàòðèöû ñîäåðæàò 64 ýëåìåíòà,
ñãðóïïèðîâàííûõ â ìàòðèöó ðàçìåðíîñòè 8õ8. Ðîâíî ñòîëüêî æå, ñêîëüêî òðèãðàìì
ñîäåðæèòñÿ â ìàòðèöå È-Öçèí. À ýòî óæå ãèïåðêóá.
Ðàññìîòðèì ãåîìåòðè÷åñêèé ñìûñë ïðîñòðàíñòâà ãèïåðêóáà.
Ðàçâåðíåì êóá â ñòðîêó òðèãðàìì è óìíîæèì íà ñîîòâåòñòâóþùèé ñòîëáåö
òðèãðàìì. â ðåçóëüòàòå ìû ìû ïîëó÷èì ìàòðèöó È-Öçèí, ðàçìåðíîñòüþ 8õ8, â êîòîðîé
ñ êàæäîé òðèãðàììîé ñâÿçàíà åå ãåîìåòðè÷åñêàÿ èíòåðïðåòàöèÿ, îòðàæàþùàÿ åå
îðèåíòàöèþ â ïðîñòðàíñòâå êóáà.
 ðèñ. 21
Êàæäûé êóáèê â ýòîé ìàòðèöå îòîæäåñòâëÿåòñÿ ñ áàçèñíîé òðèãðàììîé
È-Öçèí, îðèåíòèðîâàííîé ñîîòâåòñòâóþùèì îáðàçîì â "êóáèêå" ñîáñòâåííîãî
ïðîñòðàíñòâà.
Êàæäàÿ
ñòðîêà â ýòîé ìàòðèöå öèêëè÷åñêè ñäâèíóòà îòíîñèòåëüíî ïðåäûäóùåé âïðàâî
("ñäâèã Äîïïëåðà") íà îäèí ïîçèöèîííûé ðàçðÿä. Ïðè ýòîì
ïîñëåäíèé
ïðàâûé ðàçðÿä, âûõîäÿùèé çà ïðåäåëû "ðàçðÿäíîé" ñåòêè ñòàíîâèòñÿ â ñëåäóþùåé
ñòðîêå ïåðâûì, êàê
áû îòðàæàÿ áèáëåéñêóþ èñòèíó "è Ïîñëåäíèé ñòàíîâèòñÿ Ïåðâûì". È ýòà èñòèíà
ïðîÿâëÿåòñÿ íå òîëüêî íà ëîêàëüíûõ óðîâíÿõ. Îíà áóäåò ñïðàâåäëèâà è äëÿ
ìàòðèöû â öåëîì. Âèäèòå, â ïîñëåäíåé ñòðîêå êóáèê ¹ 8 ñòîèò íà ìåñòå
êóáèêà ¹1?
Íà ìíîãèõ ñòðàíèöàõ ñàéòà ïðèâîäèòñÿ
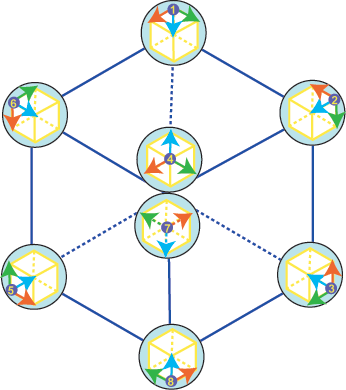
ñëåäóþùèé ðèñóíîê Äðåâíåãî Öâåòêà Æèçíè, íà êîòîðûé íàëîæåí ãèïåðêóá ÄÍÊ,
ñôîðìèðîâàííûé èç ÷åòûðåõ àçîòèñòûõ îñíîâàíèé.
ðèñ. 21
Êàæäûé êóáèê â ýòîé ìàòðèöå îòîæäåñòâëÿåòñÿ ñ áàçèñíîé òðèãðàììîé
È-Öçèí, îðèåíòèðîâàííîé ñîîòâåòñòâóþùèì îáðàçîì â "êóáèêå" ñîáñòâåííîãî
ïðîñòðàíñòâà.
Êàæäàÿ
ñòðîêà â ýòîé ìàòðèöå öèêëè÷åñêè ñäâèíóòà îòíîñèòåëüíî ïðåäûäóùåé âïðàâî
("ñäâèã Äîïïëåðà") íà îäèí ïîçèöèîííûé ðàçðÿä. Ïðè ýòîì
ïîñëåäíèé
ïðàâûé ðàçðÿä, âûõîäÿùèé çà ïðåäåëû "ðàçðÿäíîé" ñåòêè ñòàíîâèòñÿ â ñëåäóþùåé
ñòðîêå ïåðâûì, êàê
áû îòðàæàÿ áèáëåéñêóþ èñòèíó "è Ïîñëåäíèé ñòàíîâèòñÿ Ïåðâûì". È ýòà èñòèíà
ïðîÿâëÿåòñÿ íå òîëüêî íà ëîêàëüíûõ óðîâíÿõ. Îíà áóäåò ñïðàâåäëèâà è äëÿ
ìàòðèöû â öåëîì. Âèäèòå, â ïîñëåäíåé ñòðîêå êóáèê ¹ 8 ñòîèò íà ìåñòå
êóáèêà ¹1?
Íà ìíîãèõ ñòðàíèöàõ ñàéòà ïðèâîäèòñÿ
ñëåäóþùèé ðèñóíîê Äðåâíåãî Öâåòêà Æèçíè, íà êîòîðûé íàëîæåí ãèïåðêóá ÄÍÊ,
ñôîðìèðîâàííûé èç ÷åòûðåõ àçîòèñòûõ îñíîâàíèé.
 ðèñ. 22
Ïîñìîòðèòå è óâèäüòå ñîîòâåòñòâèå ìåæäó
äàííûì ðèñóíêîì è ìàòðèöåé È-Öçèí, ïðèâåäåííîé âûøå.
Êàæäûé
"êóáèê" ÄÍÊ ðàçâîðà÷èâàåòñÿ â ñîîòâåòñòâóþùóþ ñòðîêó ìàòðèöû È-Öçèí, ñ
öèêëè÷åñêèì ïîâîðîòîì â ïðîñòðàíñòâå íà 90 ãðàäóñîâ âñåõ áàçèñíûõ
âåêòîðîâ ñîîòâåòñòâóþùåé òðèãðàììû.
Ýòîò ôåíîìåí ïîëíîñòüþ àíàëîãè÷åí ôåíîìåíó èçìåíåíèÿ íåñóùåé ÷àñòîòû
èñõîäíîãî ãèïåðïðîñòðàíñòâà. Äðóãèìè ñëîâàìè, èçìåíÿåòñÿ âðåìåííîé
ðèòì ñîîòâåòñòâóþùåãî ïðîñòðàíñòâà.
 êîñìîëîãèè ýòî ïðîÿâëÿåòñÿ â ôåíîìåíå ñìåùåíèÿ ñïåêòðàëüíûõ ëèíèé ãàëàêòèê
(êðàñíîå ñìåùåíèå), êîòîðîå ñîâðåìåííîé íàóêîé òðàêòóåòñÿ êàê
"ðàçáåãàíèè ãàëàêòèê".
Íî êàæäûé "êóáèê" è
ãèïåðêóá â öåëîì ìîãóò èìåòü è èìåþò ñîáñòâåííûå òî÷êè ñáîðêè è ðàçáîðêè.
Åñëè òåïåðü ïðèíÿòü, ÷òî
W1=(W0)2=9,
òî ìû ìîæåì ïîñòðîèòü, ïî îáðàçó è ïîäîáèþ íîâîå ãèïåðïðîñòðàíñòâî.
ðèñ. 22
Ïîñìîòðèòå è óâèäüòå ñîîòâåòñòâèå ìåæäó
äàííûì ðèñóíêîì è ìàòðèöåé È-Öçèí, ïðèâåäåííîé âûøå.
Êàæäûé
"êóáèê" ÄÍÊ ðàçâîðà÷èâàåòñÿ â ñîîòâåòñòâóþùóþ ñòðîêó ìàòðèöû È-Öçèí, ñ
öèêëè÷åñêèì ïîâîðîòîì â ïðîñòðàíñòâå íà 90 ãðàäóñîâ âñåõ áàçèñíûõ
âåêòîðîâ ñîîòâåòñòâóþùåé òðèãðàììû.
Ýòîò ôåíîìåí ïîëíîñòüþ àíàëîãè÷åí ôåíîìåíó èçìåíåíèÿ íåñóùåé ÷àñòîòû
èñõîäíîãî ãèïåðïðîñòðàíñòâà. Äðóãèìè ñëîâàìè, èçìåíÿåòñÿ âðåìåííîé
ðèòì ñîîòâåòñòâóþùåãî ïðîñòðàíñòâà.
 êîñìîëîãèè ýòî ïðîÿâëÿåòñÿ â ôåíîìåíå ñìåùåíèÿ ñïåêòðàëüíûõ ëèíèé ãàëàêòèê
(êðàñíîå ñìåùåíèå), êîòîðîå ñîâðåìåííîé íàóêîé òðàêòóåòñÿ êàê
"ðàçáåãàíèè ãàëàêòèê".
Íî êàæäûé "êóáèê" è
ãèïåðêóá â öåëîì ìîãóò èìåòü è èìåþò ñîáñòâåííûå òî÷êè ñáîðêè è ðàçáîðêè.
Åñëè òåïåðü ïðèíÿòü, ÷òî
W1=(W0)2=9,
òî ìû ìîæåì ïîñòðîèòü, ïî îáðàçó è ïîäîáèþ íîâîå ãèïåðïðîñòðàíñòâî.
 Íåòðóäíî óâèäåòü, ÷òî â ýòîé ìàòðèöå (W1
)2=9õ9=81.
Ýòà áóäåò óæå ðàñøèðåííàÿ ìàòðèöà Ò-Öçèí, ðàçìåðíîñòüþ 9õ9, â êîòîðîé
êàæäàÿ òðèãðàììà ôîðìèðóåòñÿ óæå èç òðåõ áàçèñíûõ òðèãðàìì.
Íåòðóäíî óâèäåòü, ÷òî â ýòîé ìàòðèöå (W1
)2=9õ9=81.
Ýòà áóäåò óæå ðàñøèðåííàÿ ìàòðèöà Ò-Öçèí, ðàçìåðíîñòüþ 9õ9, â êîòîðîé
êàæäàÿ òðèãðàììà ôîðìèðóåòñÿ óæå èç òðåõ áàçèñíûõ òðèãðàìì.
 ðèñ. 23
Âèäèòå, ýòà ìàòðèöà â ñîäåðæèò â ñåáå 17 ÿâíûõ òî÷åê ñáîðêè-ðàçáîðêè, à
âîñåìíàäöàòàÿ òî÷êà ÿâëÿåòñÿ íåïðîÿâëåííîé. Îòìåòèì. ÷òî òî÷íî ñòîëüêî æå
âåðøèí ñîäåðæèòñÿ â òðåòüåé îáîëî÷êå Ïåðèîäè÷åñêîé ñèñòåìå õèìè÷åñêèõ
ýëåìåíòîâ
<2,2;8,8,18,18,32,32>
Èç ýòîãî ðèñóíêà ìû ñíîâà âèäèì, ÷òî êàæäàÿ ýíåàãðàììà ñîñòîèò èç òðåõ
òðèãðàìì, ò.å. ÿâëÿåòñÿ òðèãðàììîé âûñøåãî óðîâíÿ èçìåðåíèé è,
ñëåäîâàòåëüíî, ìû ñíîâà ïðèõîäèì ê íà÷àëüíîé òðèãðàììå
ðèñ. 23
Âèäèòå, ýòà ìàòðèöà â ñîäåðæèò â ñåáå 17 ÿâíûõ òî÷åê ñáîðêè-ðàçáîðêè, à
âîñåìíàäöàòàÿ òî÷êà ÿâëÿåòñÿ íåïðîÿâëåííîé. Îòìåòèì. ÷òî òî÷íî ñòîëüêî æå
âåðøèí ñîäåðæèòñÿ â òðåòüåé îáîëî÷êå Ïåðèîäè÷åñêîé ñèñòåìå õèìè÷åñêèõ
ýëåìåíòîâ
<2,2;8,8,18,18,32,32>
Èç ýòîãî ðèñóíêà ìû ñíîâà âèäèì, ÷òî êàæäàÿ ýíåàãðàììà ñîñòîèò èç òðåõ
òðèãðàìì, ò.å. ÿâëÿåòñÿ òðèãðàììîé âûñøåãî óðîâíÿ èçìåðåíèé è,
ñëåäîâàòåëüíî, ìû ñíîâà ïðèõîäèì ê íà÷àëüíîé òðèãðàììå
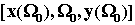 èç êîòîðîé, ïî îáðàçó è
ïîäîáèþ, ìîæíî ôîðìèðîâàòü íîâûå ãèïåðïðîñòðàíñòâà.
Ìîæåò áûòü, íàêîíåö, ê ëþäÿì ïðèäåò îñîçíàíèå òîãî, êàê ïðèðîäà ñòðîèò ñâîè
ãèïåðïðîñòàíñòâà, ÷òî ëþáîå ãèïåðïðîñòàíñòâî, ñòðîèòñÿ ïî îáðàçó è ïîäîáèþ
áàçèñíîãî òðèãðàììíîãî (òðåõìåðíîãî) ïðîñòðàíñòâà?
Èç ýòèõ áàçèñíûõ òðèãðàìì, ðàñïîëîæåííûõ â ñòðîãî îïðåäåëåííîì ïîðÿäêå íà
ïëîñêîñòè ôîðìèðóþòñÿ ãèïåðìàòðèöû, ïî êîòîðûì
ìîæíî
ïîñòðîèòü ãèïåðïðîñòðàíñòâî âûñøåãî èçìåðåíèÿ - êóá, èëè äàæå
ãèïåðêóá. Ýòî òðèâèàëüíàÿ èñòèíà íàïðî÷ü îòìåòàåò ëîæíóþ èäåþ î òîì,
÷òî "ïëîñêàðèêè"(ñóùåñòâà, æèâóùèå íà ïëîñêîñòè ), íå ìîãóò ïîçíàòü
ñâîéñòâ ïðîñòðàíñòâ âûñøèõ èçìåðåíèé.
Âïðî÷åì, ýòà èñòèíà èçâåñòíà ëþáîìó èíæåíåðó, êîòîðûé ìîæåò ïî ÷åðòåæàì
ñòðîèòü òðåõìåðíûå ïðîñòðàíñòâà âûñøèõ èçìåðåíèé. Íî åñëè
÷åëîâåê íå ìîæåò ÷èòàòü ÷åðòåæè, òî îí íèêîãäà íå ñìîæåò ìàòåðèàëèçîâàòü
Îáúåêò ïî åãî ÷åðòåæàì. Äëÿ ýòîãî íóæíû ñîîòâåòñòâóþùèå çíàíèÿ è
îáðàçîâàíèå. È ýòî èçâåñòíî âñåì.
Íî ñòðàííîå äåëî, êîãäà ìû ãîâîðèì î âûñøèõ èçìåðåíèÿõ ñîçíàíèÿ è
ìûøëåíèÿ, òî ìû äàæå íå õîòèì îñîçíàòü, ÷òî íàøè â áîëüøèíñòâå
ñëó÷àåâ ñàìîíàäåÿííûå óìîçàêëþ÷åíèÿ î âûñøèõ èçìåðåíèÿõ ñîçíàíèÿ è
ìûøëåíèÿ ÿâëÿþòñÿ ïðîñòî íåâåæåñòâåííûìè.
Î ëþäÿõ, íå ñïîñîáíûõ âûéòè çà ïðåäåëû ñâîåãî "ïëîñêîñòíîãî" ìûøëåíèÿ, è
ïðèáëèçèòüñÿ ê âûñøåìó Ñîçíàíèþ Òâîðöà, ìîæíî ñêàçàòü, ÷òî "ðîæäåííûå
ïîëçàòü ëåòàòü íå ìîãóò". Îíè áóäóò áåñêîíå÷íî âðàùàòüñÿ ïî êðóãó, èç
êîòîðîãî íåò âûõîäà. Îíè ìîãóò áûòü òàëàíòëèâûìè îðãàíèçàòîðàìè íàóêè, îíè
ìîãóò áûòü òàëàíòëèâûìè àíàëèòèêàìè, ðàñ÷ëåíÿÿ öåëîå íà ÷àñòè, íî îíè
íèêîãäà íå ñòàíóò ñèíòåçàòîðàìè êà÷åñòâåííî íîâûõ çíàíèé, ëåæàùèõ íà
ïðåäåëàìè "ïëîñêîñòè ìûøëåíèÿ".
ß íå
ïðåòåíäóþ íà èñòèíó â ïîñëåäíåé èíñòàíöèè. ß äåëàþ âñåãî ëèøü ïåðâûå øàãè â
íóæíîì íàïðàâëåíèè. Åäèíîå çíàíèå, Åäèíûé çàêîí ýâîëþöèè äâîéñòâåííîãî
îòíîøåíèÿ ïîçâîëÿåò óòâåðæäàòü, ÷òî è ñîçíàíèå è ìûøëåíèå ëþäåé ÿâëÿåòñÿ
ìíîãîóðîâíåâûì è ñòðóêòóðèðóåìûì.
7.
ÃÈÏÅÐÌÀÒÐÈÖÀ
ÈÊÎÑÀÝÄÐÀ
Âûøå ìû ïîäðîáíî
ðàññìîòðåëè ñâîéñòâà êóáè÷åñêîãî ãèïåðïðîñòðàíñòâà.
Îäíàêî
Ïëàòîíîâû òåëà íåñóò
â ñåáå ìàòåðèíñêèé (èíüñêèé àñïåêòû) è ïîòîìó îíè ìîãóò ôîðìèðîâàòü,
ïî îáðàçó è ïîäîáèþ, ñîáñòâåííûå ìíîãîìåðíûå ãèïåðêðèñòàëëû è
ñîîòâåòñòâóþùèå ãèïåðìàòðèöû, â êîòîðûå îíè ìîãóò ñâîðà÷èâàòüñÿ è èç êîòîðûõ
îíè ìîãóò ðàçâîðà÷èâàòüñÿ.
Íà ñòðàíèöå "Ñïèíîðû è òåíçîðû" ìû óæå îïèñûâàëè
ñâîéñòâà ýòîé ãèïåðìàòðèöû
èç êîòîðîé, ïî îáðàçó è
ïîäîáèþ, ìîæíî ôîðìèðîâàòü íîâûå ãèïåðïðîñòðàíñòâà.
Ìîæåò áûòü, íàêîíåö, ê ëþäÿì ïðèäåò îñîçíàíèå òîãî, êàê ïðèðîäà ñòðîèò ñâîè
ãèïåðïðîñòàíñòâà, ÷òî ëþáîå ãèïåðïðîñòàíñòâî, ñòðîèòñÿ ïî îáðàçó è ïîäîáèþ
áàçèñíîãî òðèãðàììíîãî (òðåõìåðíîãî) ïðîñòðàíñòâà?
Èç ýòèõ áàçèñíûõ òðèãðàìì, ðàñïîëîæåííûõ â ñòðîãî îïðåäåëåííîì ïîðÿäêå íà
ïëîñêîñòè ôîðìèðóþòñÿ ãèïåðìàòðèöû, ïî êîòîðûì
ìîæíî
ïîñòðîèòü ãèïåðïðîñòðàíñòâî âûñøåãî èçìåðåíèÿ - êóá, èëè äàæå
ãèïåðêóá. Ýòî òðèâèàëüíàÿ èñòèíà íàïðî÷ü îòìåòàåò ëîæíóþ èäåþ î òîì,
÷òî "ïëîñêàðèêè"(ñóùåñòâà, æèâóùèå íà ïëîñêîñòè ), íå ìîãóò ïîçíàòü
ñâîéñòâ ïðîñòðàíñòâ âûñøèõ èçìåðåíèé.
Âïðî÷åì, ýòà èñòèíà èçâåñòíà ëþáîìó èíæåíåðó, êîòîðûé ìîæåò ïî ÷åðòåæàì
ñòðîèòü òðåõìåðíûå ïðîñòðàíñòâà âûñøèõ èçìåðåíèé. Íî åñëè
÷åëîâåê íå ìîæåò ÷èòàòü ÷åðòåæè, òî îí íèêîãäà íå ñìîæåò ìàòåðèàëèçîâàòü
Îáúåêò ïî åãî ÷åðòåæàì. Äëÿ ýòîãî íóæíû ñîîòâåòñòâóþùèå çíàíèÿ è
îáðàçîâàíèå. È ýòî èçâåñòíî âñåì.
Íî ñòðàííîå äåëî, êîãäà ìû ãîâîðèì î âûñøèõ èçìåðåíèÿõ ñîçíàíèÿ è
ìûøëåíèÿ, òî ìû äàæå íå õîòèì îñîçíàòü, ÷òî íàøè â áîëüøèíñòâå
ñëó÷àåâ ñàìîíàäåÿííûå óìîçàêëþ÷åíèÿ î âûñøèõ èçìåðåíèÿõ ñîçíàíèÿ è
ìûøëåíèÿ ÿâëÿþòñÿ ïðîñòî íåâåæåñòâåííûìè.
Î ëþäÿõ, íå ñïîñîáíûõ âûéòè çà ïðåäåëû ñâîåãî "ïëîñêîñòíîãî" ìûøëåíèÿ, è
ïðèáëèçèòüñÿ ê âûñøåìó Ñîçíàíèþ Òâîðöà, ìîæíî ñêàçàòü, ÷òî "ðîæäåííûå
ïîëçàòü ëåòàòü íå ìîãóò". Îíè áóäóò áåñêîíå÷íî âðàùàòüñÿ ïî êðóãó, èç
êîòîðîãî íåò âûõîäà. Îíè ìîãóò áûòü òàëàíòëèâûìè îðãàíèçàòîðàìè íàóêè, îíè
ìîãóò áûòü òàëàíòëèâûìè àíàëèòèêàìè, ðàñ÷ëåíÿÿ öåëîå íà ÷àñòè, íî îíè
íèêîãäà íå ñòàíóò ñèíòåçàòîðàìè êà÷åñòâåííî íîâûõ çíàíèé, ëåæàùèõ íà
ïðåäåëàìè "ïëîñêîñòè ìûøëåíèÿ".
ß íå
ïðåòåíäóþ íà èñòèíó â ïîñëåäíåé èíñòàíöèè. ß äåëàþ âñåãî ëèøü ïåðâûå øàãè â
íóæíîì íàïðàâëåíèè. Åäèíîå çíàíèå, Åäèíûé çàêîí ýâîëþöèè äâîéñòâåííîãî
îòíîøåíèÿ ïîçâîëÿåò óòâåðæäàòü, ÷òî è ñîçíàíèå è ìûøëåíèå ëþäåé ÿâëÿåòñÿ
ìíîãîóðîâíåâûì è ñòðóêòóðèðóåìûì.
7.
ÃÈÏÅÐÌÀÒÐÈÖÀ
ÈÊÎÑÀÝÄÐÀ
Âûøå ìû ïîäðîáíî
ðàññìîòðåëè ñâîéñòâà êóáè÷åñêîãî ãèïåðïðîñòðàíñòâà.
Îäíàêî
Ïëàòîíîâû òåëà íåñóò
â ñåáå ìàòåðèíñêèé (èíüñêèé àñïåêòû) è ïîòîìó îíè ìîãóò ôîðìèðîâàòü,
ïî îáðàçó è ïîäîáèþ, ñîáñòâåííûå ìíîãîìåðíûå ãèïåðêðèñòàëëû è
ñîîòâåòñòâóþùèå ãèïåðìàòðèöû, â êîòîðûå îíè ìîãóò ñâîðà÷èâàòüñÿ è èç êîòîðûõ
îíè ìîãóò ðàçâîðà÷èâàòüñÿ.
Íà ñòðàíèöå "Ñïèíîðû è òåíçîðû" ìû óæå îïèñûâàëè
ñâîéñòâà ýòîé ãèïåðìàòðèöû
 ðèñ.
24
Â
ýòîé ìàòðèöå ñèìâîëû
G, U,
C, A
èìåþò ñìûñë
àçîòèñòûõ îñíîâàíèé ãåíåòè÷åñêîãî êîäà, ôîðìèðóþùèõ âåñû äâîéñòâåííîãî
îòíîøåíèÿ.
Íåòðóäíî
óâèäåòü, ÷òî ìàòðèöà ãèïåðèêîñàýäðà ÿâëÿåòñÿ ïðååìñòâåííîé ïî îòíîøåíèþ ê êóáó. Îíà ñîñòîèò
èç 9-òè ñåêòîðîâ, ôîðìèðóþùèõ ãèïåðêóá, êàæäàÿ âåðøèíà êîòîðîãî ñîñòîèò èç
4-õ êëåòî÷íûõ ìàòðèö-êðåñòîâ (òåòðàýäðîâ).
Âîò è îòâåò íà âîïðîñ, ïî÷åìó îêòàýäð è êóá, èêîñàýäð è äîäåêàýäð ÿâëÿþòñÿ
âçàèìíûìè, à òåòðàýäð è îêòàýäð, êóá è èêîñàýäð êàê áû ñòîÿò îòäåëüíî.
"Îãíåííàÿ" ìàòðèöà, ÿâëÿþùàÿñÿ Âåëèêèì ïðåäåëîì ãèïåðòåòðàýäðà (ðèñ. 20),
ôîðìèðóåò âçàèìîäîïîëíèòåëüíóþ îãíåííóþ ìàòðèöó, êîòîðàÿ ðàçâîðà÷èâàåòñÿ â
íîâûé ãèïåðòåòðàýäð, âçàèìîäîïîëíèòåëüíûé ïåðâîìó.
Â
ðåçóëüòàòå ìû è ïîëó÷àåì Êóá ãèïåðèêîñàýäðà.
ðèñ.
24
Â
ýòîé ìàòðèöå ñèìâîëû
G, U,
C, A
èìåþò ñìûñë
àçîòèñòûõ îñíîâàíèé ãåíåòè÷åñêîãî êîäà, ôîðìèðóþùèõ âåñû äâîéñòâåííîãî
îòíîøåíèÿ.
Íåòðóäíî
óâèäåòü, ÷òî ìàòðèöà ãèïåðèêîñàýäðà ÿâëÿåòñÿ ïðååìñòâåííîé ïî îòíîøåíèþ ê êóáó. Îíà ñîñòîèò
èç 9-òè ñåêòîðîâ, ôîðìèðóþùèõ ãèïåðêóá, êàæäàÿ âåðøèíà êîòîðîãî ñîñòîèò èç
4-õ êëåòî÷íûõ ìàòðèö-êðåñòîâ (òåòðàýäðîâ).
Âîò è îòâåò íà âîïðîñ, ïî÷åìó îêòàýäð è êóá, èêîñàýäð è äîäåêàýäð ÿâëÿþòñÿ
âçàèìíûìè, à òåòðàýäð è îêòàýäð, êóá è èêîñàýäð êàê áû ñòîÿò îòäåëüíî.
"Îãíåííàÿ" ìàòðèöà, ÿâëÿþùàÿñÿ Âåëèêèì ïðåäåëîì ãèïåðòåòðàýäðà (ðèñ. 20),
ôîðìèðóåò âçàèìîäîïîëíèòåëüíóþ îãíåííóþ ìàòðèöó, êîòîðàÿ ðàçâîðà÷èâàåòñÿ â
íîâûé ãèïåðòåòðàýäð, âçàèìîäîïîëíèòåëüíûé ïåðâîìó.
Â
ðåçóëüòàòå ìû è ïîëó÷àåì Êóá ãèïåðèêîñàýäðà.
 ðèñ. 25
Ìîæíî ñêàçàòü, ÷òî êàæäàÿ
êëåòî÷íàÿ ìàòðèöà (1-9) ÿâëÿåòñÿ ïðîåêöèåé íà
ïëîñêîñòü äâóõ âçàèìîäîïîëíèòåëüíûõ çâåçäíûõ òåòðàýäðîâ
(ðèñ. 19).
Õî÷åòñÿ ïðåäóïðåäèòü ìàòåìàòèêîâ, êîòîðûå ïîïûòàþòñÿ ðåøèòü çàäà÷ó
ñâîðà÷èâàíèÿ ãèïåðèêîñàýäðà ê äâóìåðíîìó âèäó, ÷òî, ïðèðîäà ïðè
ñâîðà÷èâàíèè è ðàçâîðà÷èâàíèè ñîáñòâåííûõ ãèïåðïðîñòðàíñòâ, èñïîëüçóåò,
âèäèìî, òàêèå
èíâàðèàíòíûå ïðåîáðàçîâàíèÿ, ïðè êîòîðûõ ñîõðàíÿþòñÿ ñâîéñòâà
ñèììåòðèè ãèïåðïðîñòðàíñòâà âûñøåãî óðîâíÿ.
Íåòðóäíî îñîçíàòü, ÷òî â öåíòðå òàêîãî ãèïåðêðèñòàëëà òàêæå ñîäåðæèòñÿ
Âåëèêèé ïðåäåë -äåâÿòàÿ âåðøèíà, íî ñîñòîÿùàÿ óæå èç 4-õ êëåòî÷íûõ ìàòðèö,
ôîðìèðóþùèõ åäèíóþ ìàòðèöó ðàçìåðíîñòüþ 4õ4.Îíà è áóäåò ÿâëÿòüñÿ 13-é
âåðøèíîé ãèïåðèêîñàýäðà, íàõîäÿùåéñÿ â öåíòðå ýòîãî ãèïåðêðèñòàëëà.
Îäíàêî ñàìîé ñîâåðøåííîé ìàòðèöåé ÄÍÊ
ãèïåðïðîñòðàíñòâà-ãèïåðâðåìåíè áóäåò ÿâëÿòüñÿ ìàòðèöà
ñàìîãî ñîâåðøåííîãî Ïëàòîíîâîãî ãèïåðêðèñòàëëà-ãèïåðäîäåêàýäðà.Ïîñêîëüêó â
äîäåêàýäðå ñîäåðæèòñÿ 20 âåðøèí è 12 ãðàíåé, è îí ÿâëÿåòñÿ âçàèìîäîïîëíèòåëüíûì
èêîñàýäðó, òî, ïî îáðàçó è ïîäîáèþ, ìàòðèöà ãèïåðäîäåêàýäðà äîëæíà èìåòü
ðàçìåðíîñòü 20õ20.
Íà ñòðàíèöå "Ñïèíîðû è òåíçîðû"
ìû óæå îïèñûâàëè ñâîéñòâà è ýòîé ãèïåðìàòðèöû.
ðèñ. 25
Ìîæíî ñêàçàòü, ÷òî êàæäàÿ
êëåòî÷íàÿ ìàòðèöà (1-9) ÿâëÿåòñÿ ïðîåêöèåé íà
ïëîñêîñòü äâóõ âçàèìîäîïîëíèòåëüíûõ çâåçäíûõ òåòðàýäðîâ
(ðèñ. 19).
Õî÷åòñÿ ïðåäóïðåäèòü ìàòåìàòèêîâ, êîòîðûå ïîïûòàþòñÿ ðåøèòü çàäà÷ó
ñâîðà÷èâàíèÿ ãèïåðèêîñàýäðà ê äâóìåðíîìó âèäó, ÷òî, ïðèðîäà ïðè
ñâîðà÷èâàíèè è ðàçâîðà÷èâàíèè ñîáñòâåííûõ ãèïåðïðîñòðàíñòâ, èñïîëüçóåò,
âèäèìî, òàêèå
èíâàðèàíòíûå ïðåîáðàçîâàíèÿ, ïðè êîòîðûõ ñîõðàíÿþòñÿ ñâîéñòâà
ñèììåòðèè ãèïåðïðîñòðàíñòâà âûñøåãî óðîâíÿ.
Íåòðóäíî îñîçíàòü, ÷òî â öåíòðå òàêîãî ãèïåðêðèñòàëëà òàêæå ñîäåðæèòñÿ
Âåëèêèé ïðåäåë -äåâÿòàÿ âåðøèíà, íî ñîñòîÿùàÿ óæå èç 4-õ êëåòî÷íûõ ìàòðèö,
ôîðìèðóþùèõ åäèíóþ ìàòðèöó ðàçìåðíîñòüþ 4õ4.Îíà è áóäåò ÿâëÿòüñÿ 13-é
âåðøèíîé ãèïåðèêîñàýäðà, íàõîäÿùåéñÿ â öåíòðå ýòîãî ãèïåðêðèñòàëëà.
Îäíàêî ñàìîé ñîâåðøåííîé ìàòðèöåé ÄÍÊ
ãèïåðïðîñòðàíñòâà-ãèïåðâðåìåíè áóäåò ÿâëÿòüñÿ ìàòðèöà
ñàìîãî ñîâåðøåííîãî Ïëàòîíîâîãî ãèïåðêðèñòàëëà-ãèïåðäîäåêàýäðà.Ïîñêîëüêó â
äîäåêàýäðå ñîäåðæèòñÿ 20 âåðøèí è 12 ãðàíåé, è îí ÿâëÿåòñÿ âçàèìîäîïîëíèòåëüíûì
èêîñàýäðó, òî, ïî îáðàçó è ïîäîáèþ, ìàòðèöà ãèïåðäîäåêàýäðà äîëæíà èìåòü
ðàçìåðíîñòü 20õ20.
Íà ñòðàíèöå "Ñïèíîðû è òåíçîðû"
ìû óæå îïèñûâàëè ñâîéñòâà è ýòîé ãèïåðìàòðèöû.
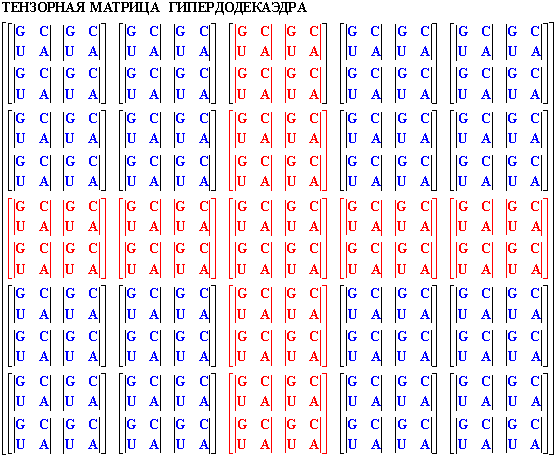 ðèñ.
26
Âåëèêèå ïðåäåëû äàííîé êëåòî÷íîé ãèïåðìàòðèöû ôîðìèðóþò ìàòðèöó
Âåëèêèé ïðåäåëîâ ðàçìåðíîñòüþ 5õ5. Ýòè Âåëèêèå ïðåäåëû ðàçâîðà÷èâàþòñÿ
âíà÷àëå â "îãíåííûé êðåñò", ñîñòîÿùèé èç 9-òè êëåòî÷íûõ ìàòðèö
-ãèïåðòåòðàýäðîâ(ðèñ.19). Îãíåííûé êðåñò
ñíîâà äåëèò âñå ïðîñòðàíñòâî ãèïåðìàòðèöû íà 4 -å âçàìîäîïîëíèòåëüíûõ ñåêòîðà,
êàæäûé èç êîòîðûõ ôîðìèðóåòñÿ èç 4-õ áàçèñíûõ êëåòî÷íûõ ñåêòîðîâ
(ðèñ.19).
Èñïîëüçóÿ ðèñ. 19, òåïåðü íåòðóäíî, ïî îáðàçó è ïîäîáèþ, çàïèñàòü äàííóþ
ãèïåðìàòðèöó â èíîì âèäå
ðèñ.
26
Âåëèêèå ïðåäåëû äàííîé êëåòî÷íîé ãèïåðìàòðèöû ôîðìèðóþò ìàòðèöó
Âåëèêèé ïðåäåëîâ ðàçìåðíîñòüþ 5õ5. Ýòè Âåëèêèå ïðåäåëû ðàçâîðà÷èâàþòñÿ
âíà÷àëå â "îãíåííûé êðåñò", ñîñòîÿùèé èç 9-òè êëåòî÷íûõ ìàòðèö
-ãèïåðòåòðàýäðîâ(ðèñ.19). Îãíåííûé êðåñò
ñíîâà äåëèò âñå ïðîñòðàíñòâî ãèïåðìàòðèöû íà 4 -å âçàìîäîïîëíèòåëüíûõ ñåêòîðà,
êàæäûé èç êîòîðûõ ôîðìèðóåòñÿ èç 4-õ áàçèñíûõ êëåòî÷íûõ ñåêòîðîâ
(ðèñ.19).
Èñïîëüçóÿ ðèñ. 19, òåïåðü íåòðóäíî, ïî îáðàçó è ïîäîáèþ, çàïèñàòü äàííóþ
ãèïåðìàòðèöó â èíîì âèäå
 ðèñ.
27
 ýòîé ìàòðèöå áàçèñíàÿ êëåòî÷íàÿ ìàòðèöà (ðèñ. 19) ôîðìèðóåò ãèïåðìàòðèöó
ðàçìåðíîñòüþ 5õ5.
Íà
ñòðàíèöå "Î ïîäîáèè Âñåëåííûõ"
áûë ïðèâåäåí ñëåäóþùèé ðèñóíîê èç êíèãè Ñóõîíîñà
"Ìàñøòàáíàÿ ãàðìîíèÿ Âñåëåííîé"[64],
èç êîòîðîãî íåïîñðåäñòâåííî ñëåäóåò ÷òî â îñíîâå
ìàñøòàáíîé ãàðìîíèè âñåëåííîé
ëåæèò êîýôôèöèåíò, êðàòíûé 5.
ðèñ.
27
 ýòîé ìàòðèöå áàçèñíàÿ êëåòî÷íàÿ ìàòðèöà (ðèñ. 19) ôîðìèðóåò ãèïåðìàòðèöó
ðàçìåðíîñòüþ 5õ5.
Íà
ñòðàíèöå "Î ïîäîáèè Âñåëåííûõ"
áûë ïðèâåäåí ñëåäóþùèé ðèñóíîê èç êíèãè Ñóõîíîñà
"Ìàñøòàáíàÿ ãàðìîíèÿ Âñåëåííîé"[64],
èç êîòîðîãî íåïîñðåäñòâåííî ñëåäóåò ÷òî â îñíîâå
ìàñøòàáíîé ãàðìîíèè âñåëåííîé
ëåæèò êîýôôèöèåíò, êðàòíûé 5.
 ðèñ.
28
Êîììåíòàðèè, âèäèìî èçëèøíè. Êðóã çàìûêàåòñÿ íà ÷èñëå 5. Ýâîëþöèÿ âñåõ
ñîâåðøåííûõ ãèïåð Ïëàòîíîâûõ òåë îêàçûâàåòñÿ êðàòíîé ÷èñëó 5.
Íî äàæå è ýòà ñàìàÿ ñîâåðøåííàÿ ìàòðèöà ÄÍÊ ìîæåò ñâîðà÷èâàòüñÿ â
×èñëî-íóëüìåðíîå ãèïåðïðîñòðàíñòâî.
Ýòî îçíà÷àò òàêæå, ÷òî äàæå ñàìàÿ ñîâåðøåííàÿ ìàòðèöà ìèðîçäàíèÿ îáëàäàåò
êîðïóñêóëÿðíî-âîëíîâûìè ñâîéñòâàìè, ïðîÿâëÿÿñü â Áûòèå (ìàòåðèàëèçàöèÿ) è
ðàñòâîðÿÿñü â Íåáûòèå (äåìàòåðèàëèçàöèÿ) è ÷òî îíà ìîæåò
îòðàæàòü êàê ÿíñêèé (ìóæñêîé), òàê è èíüñêèé (æåíñêèé) àñïåêòû.
Êàæäàÿ ìàòðèöà ÄÍÊ
èìååò ñîáñòâåííîãî Òâîðöà, êîòîðûé ïðîÿâëÿÿñü ñîâåðøàåò â ñîáñòâåííîé ìàòðèöå
ïîëíûé êðóãîîáîðîò (öèêë). Ïðåáûâàíèå Òâîðöà â îäíîì èç ïðîÿâëåííûõ ñîñòîÿíèé
ñîáñòâåííîé ìàòðèöû Òâîðåíèÿ â ýçîòåðèêå íàçûâàþò Äíÿìè Áðàìû. Ôàçîâûé ïåðåõîä
èç îäíîãî äèñêðåòíîãî (ïðîÿâëåííîãî) ñîñòîÿíèÿ â äðóãîå â ýçîòåðèêå íàçûâàþò
Íî÷àìè Áðàìû.
È òîãäà, êîãäà çàâåðøàåòñÿ ïîëíûé êðóãîîáîðîò ïî ìàòðèöå Òâîðåíèÿ, òî
ïðîèñõîäèò ôàçîâûé ïåðåõîä Òâîðöà ê êà÷åñòâåííî íîâîìó ñîñòîÿíèþ. Îí íà÷èíàåò
ïðîÿâëÿòü ñîáñòâåííóþ ìàòðèöó âûñøåãî èçìåðåíèÿ, îñòàòüñÿ â òîì æå ñîñòîÿíèè,
èëè äàæå ïåðåéòè ê ìàòðèöå íèçøåãî èçìåðåíèÿ.
Äëÿ Òâîðöà ýòî ñîñòîÿíèå ïî åãî ñîáñòâåííîìó êàëåíäàðþ îçíà÷àåò Ãîä Áðàìû.
Íåòðóäíî îñîçíàòü, ÷òî
Äíè è Íî÷è Áðàìû, Ãîäà Áðàìû â êàæäîì ìèðîçäàíèè èìåþò ñîáñòâåííûå áàçèñíîå
âðåìÿ è ðàçìåðíîñòü.
ðèñ.
28
Êîììåíòàðèè, âèäèìî èçëèøíè. Êðóã çàìûêàåòñÿ íà ÷èñëå 5. Ýâîëþöèÿ âñåõ
ñîâåðøåííûõ ãèïåð Ïëàòîíîâûõ òåë îêàçûâàåòñÿ êðàòíîé ÷èñëó 5.
Íî äàæå è ýòà ñàìàÿ ñîâåðøåííàÿ ìàòðèöà ÄÍÊ ìîæåò ñâîðà÷èâàòüñÿ â
×èñëî-íóëüìåðíîå ãèïåðïðîñòðàíñòâî.
Ýòî îçíà÷àò òàêæå, ÷òî äàæå ñàìàÿ ñîâåðøåííàÿ ìàòðèöà ìèðîçäàíèÿ îáëàäàåò
êîðïóñêóëÿðíî-âîëíîâûìè ñâîéñòâàìè, ïðîÿâëÿÿñü â Áûòèå (ìàòåðèàëèçàöèÿ) è
ðàñòâîðÿÿñü â Íåáûòèå (äåìàòåðèàëèçàöèÿ) è ÷òî îíà ìîæåò
îòðàæàòü êàê ÿíñêèé (ìóæñêîé), òàê è èíüñêèé (æåíñêèé) àñïåêòû.
Êàæäàÿ ìàòðèöà ÄÍÊ
èìååò ñîáñòâåííîãî Òâîðöà, êîòîðûé ïðîÿâëÿÿñü ñîâåðøàåò â ñîáñòâåííîé ìàòðèöå
ïîëíûé êðóãîîáîðîò (öèêë). Ïðåáûâàíèå Òâîðöà â îäíîì èç ïðîÿâëåííûõ ñîñòîÿíèé
ñîáñòâåííîé ìàòðèöû Òâîðåíèÿ â ýçîòåðèêå íàçûâàþò Äíÿìè Áðàìû. Ôàçîâûé ïåðåõîä
èç îäíîãî äèñêðåòíîãî (ïðîÿâëåííîãî) ñîñòîÿíèÿ â äðóãîå â ýçîòåðèêå íàçûâàþò
Íî÷àìè Áðàìû.
È òîãäà, êîãäà çàâåðøàåòñÿ ïîëíûé êðóãîîáîðîò ïî ìàòðèöå Òâîðåíèÿ, òî
ïðîèñõîäèò ôàçîâûé ïåðåõîä Òâîðöà ê êà÷åñòâåííî íîâîìó ñîñòîÿíèþ. Îí íà÷èíàåò
ïðîÿâëÿòü ñîáñòâåííóþ ìàòðèöó âûñøåãî èçìåðåíèÿ, îñòàòüñÿ â òîì æå ñîñòîÿíèè,
èëè äàæå ïåðåéòè ê ìàòðèöå íèçøåãî èçìåðåíèÿ.
Äëÿ Òâîðöà ýòî ñîñòîÿíèå ïî åãî ñîáñòâåííîìó êàëåíäàðþ îçíà÷àåò Ãîä Áðàìû.
Íåòðóäíî îñîçíàòü, ÷òî
Äíè è Íî÷è Áðàìû, Ãîäà Áðàìû â êàæäîì ìèðîçäàíèè èìåþò ñîáñòâåííûå áàçèñíîå
âðåìÿ è ðàçìåðíîñòü.
РЕЗЮМЕ
1. Платоновы тела наглядно демонстрируют многомерность нашего мира, а
универсальный закон эволюции двойственного отношения (монады) характеризует
периодичность изменения этой многомерности, ограниченность и замкнутость
собственных пространств.
2. Периодичность изменений свойств собственных пространств позволяет
осуществлять инвариантные преобразования (свертки и развертки этих пространств),
и формировать таким образом все более сложные и сложные пространства.
Эти же свойства позволяют осуществлять свертки собственных пространств высших
измерений к собственным пространствам меньшей мерности, без
искажений синтаксиса и семантики свернутых пространств, т.к. инвариантность
преобразований позволяет проводить развертку свернутых собственных пространств
без искажений.

e-mail:
С
благодарностью приму все ваши замечания, предложения,
с признательностью
отвечу на ваши вопросы
|

 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©