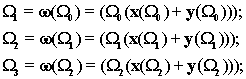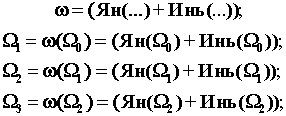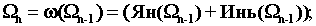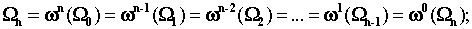СТРУКТУРЫ
1. СТРУКТУРЫ. ОСНОВНЫЕ СПОСОБЫ ПРЕДСТАВЛЕНИЯ
Любые иерархические структуры представляют
собой систему вложенных друг в друга оболочек и подоболочек.
Многие
структуры можно рассматривать и как
алгебраическую формулу, содержащую вложенные скобки
 рис. 1.
Число различных способов представления
иерархических структур само по себе является прекрасным доказательством того,
насколько эти структуры важны в повседневной жизни. Например, оглавления книг
имеют иерархическую структуру. Причём способ, чаще всего используемый для
нумерации их разделов, является ещё одним, древовидным способом представления
иерархических структур. Такой метод часто называют десятичной системой
обозначений, по аналогии с классификационной схемой, применяемой в библиотеках.
Существует тесная связь между десятичной
системой, используемой для изображения иерархических структур и способом
обозначения переменных, снабженных индексами.
Обычно элементы - образующие структуры, могут содержать гораздо больше
структурных связей, чем их можно изобразить. Поэтому в каждом конкретном случае
необходимо решать, насколько подробно мы должны описывать элементы структуры, и
в соответствии с этим выбирать тот или иной уровень формального описания. Чтобы
принять нужное решение, необходимо рассматривать не только структуру, но и класс
операций, которые будут выполняться над элементами структуры. Другими словами,
структурное представление классификации в равной степени определяется требуемыми
от элементов функциями и присущими им свойствами. Такое выделение «функций»
наравне с «формой» в большинстве случаев является основополагающим. Существуют
много других способов представления иерархических структур. Ниже будут
рассмотрены некоторые наиболее важные способы изображения этих структур, которые
используются в самых различных приложениях. Но при любых способах изображения
между любыми соседними элементами, входящими в состав структуры, существуют
изначально двойственные связи. Именно их совокупность и образует
мультидвойственную структуру того или иного класса.
1.1. ЛИНЕЙНЫЕ СТРУКТУРЫ.
Линейные структуры являются самым простым
случаем иерархических структур, когда на каждом уровне иерархии может находиться
только одна структурная единица - элемент структуры. В этом случае мы будем
иметь упорядоченное множество, состоящее из n элементов
x1, x2, x3,…,
xn.
Структурные свойства этого множества по сути
ограничиваются лишь линейным (одномерным) относительным положением элементов, т.
е. теми условиями, что если n > 0, то x1 является первым элементом (корнем
структуры), если 1<k<n, то k-му элементу предшествует xk-1, за ним следует
элемент xk+1, элемент xn-есть последний элемент (лист) структуры. Поскольку в
иерархических структурах упорядочение элементов осуществляется в соответствии с
их структурной «сложностью», отражающей преемственность их строения, то мы будем
иметь линейные структуры вида
x1 É
x2 É
x3 É…
Éxn
Линейные структуры данного
вида будем называть восходящими.
x1 Ì
x2 Ì
x3 Ì…
Éxn.
Линейные структуры
данного вида будем
называть нисходящими линейными структурами.
1.2. ДРЕВОВИДНЫЕ СТРУКТУРЫ.
Древовидные структуры являются, видимо, одними из
самых «древних» структур, которые в течение многих веков постоянно находили и
находят множество применений (особенно генеалогические деревья). Как формально
определённый математический объект дерево впервые появилось, по-видимому, в
работах Г. Кирхгоффа, который, исследуя законы, носящие сейчас его имя,
использовал деревья для нахождения множества фундаментальных циклов в
электрической цепи. Формально можно определить дерево как конечное множество
Т,
состоящее из одного или более узлов, таких, что
- имеется один специально обозначенный узел,
называемый корнем дерева,
- остальные узлы (исключая корень)
содержатся в m і попарно не пересекающихся
множествах Т1, Т2..., Tn, каждое их
которых в свою очередь является деревом.
Деревья Т1, Т2, …, Тm называются поддеревьями данного
корня. Это определение является рекурсивным, т. е. мы определили дерево в
терминах самих же деревьев. Такое определение является более естественной
характеристикой подобных структур.
Действительно, рекурсивный характер деревьев налицо
также и в природе, поскольку почки молодого дерева вырастают в ветви, имеющие
собственные почки, которые дают новые ветви и т. д. Из определения следует, что
каждый узел дерева является корнем некоторого поддерева, которое содержится в
этом дереве. Следует также отметить, что порядок следований поддеревьев
Т1,…,Тm
имеет значение.
1.3. ИЕРАРХИЧЕСКИЕ ДРЕВОВИДНЫЕ СТРУКТУРЫ.
Это деревья, каждый узел которых, исключая корень и
листья, может содержать от одного до m поддеревьев. Будем говорить, что корень
дерева является самым старшим уровнем иерархии (нулевой уровень), совокупность
узлов, входящих в корень, образуют первый уровень иерархии, совокупность узлов,
входящих в узлы первого уровня иерархии, характеризуют её второй уровень и т.д.
Листья образуют последний, самый младший уровень иерархии.
1.3.1. СЕТЕВЫЕ СТРУКТУРЫ
Этот тип структур также имеет самое широкое применение
в различных приложениях. Эти структуры являются иерархическими (многоуровневыми)
интегрированными структурами. Для изображения сетевых структур можно
использовать также самые различные способы. Сетевая структура во многих случаях
является древовидной, но такой, в которой на самом старшем уровне иерархии
находится только один элемент (корень структуры) и на самом младшем уровне
иерархии также находится один элемент (лист структуры). В сетевой структуре
любой элемент может быть связан с любым другим элементом. Сетевые структуры
являются также наиболее важными иерархическими структурами. Так, генеалогические
деревья являются древовидными структурами только потому, что не включают женщин.
Однако если учесть, что каждый человек имеет двух родителей, то вместо
генеалогического дерева мы получили бы более общую иерархическую структуру -
сетевую. Существуют и другие, широко используемые в математике и других
приложениях, способы изображения структур. Но в то же время, исходя из отношений
мультидвойственности между элементами любой системы, всегда существует
возможность осуществить разложение системы на части и изобразить отдельные ее
компоненты, или даже всю систему, в виде двоичных деревьев.
1.3.2. ГРАФЫ
Чем сложнее система, тем выше ее уровень интеграции,
тем более сложной будет ее структура, тем чаще нам придется изображать ее в виде
сети, или графа. Такие структуры присущи в первую очередь сложным
интегрированным системам. Наиболее простым и употребительным способом
представления отношений иерархии n - го порядка является представление отношений
порядка на конечных упорядоченных множествах ориентированными графами. Чаще
всего граф задаётся множеством вершин Х и соответствия Г, показывающего,
как связаны между собой вершины. Соответствие Г называется отображением
множества Х в X, т. е. граф обозначается парой G= (X, Г).
1.4. ИЕРАРХИЧЕСКИЕ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ.
Жизнеспособность позиционных систем
счисления свидетельствует о том, что они отражают самую фундаментальную
закономерность нашего мира – его иерархию и вложенность явлений и объектов друг
в друга. В основу позиционных систем заложены ограниченные наборы символов
(чисел), которые играют роль их базисных элементов. Эти элементы строго
упорядочены. Как только мы выходим за пределы этого набора, происходит
“замыкание” системы, которое сигнализирует о том, что родился еще один новый,
более сложный элемент, с более высоким уровнем иерархии. В зависимости от того,
какое основание системы счисления принято за базисное, будет определяться и
название этой позиционной системы счисления. Если мы при каждом переходе к
новому старшему индексу позиционной системы будем по определенным правилам
менять ее основание, т. е. набор базисных символов (чисел) данного индекса, то
получим иерархическую позиционную систему счисления, частным случаем которой
будет являться любая другая позиционная система счисления. Такие иерархические
системы счисления могут быть использованы во многих разделах естествознания для
описания и классификации явлений и объектов окружающей действительности. В этом
случае число, характеризующее местоположение элемента в древовидной структуре,
будет не только количественно, но качественно оценивать ее уровень сложности.
Любое число в той или иной позиционной системе счисления можно изобразить в виде
некоторой структуры. Широкая распространенность позиционных систем отражает
фундаментальный принцип ограниченности и замкнутости отношений в реальном мире.
Но в реальном мире каждый уровень иерархии системы может иметь свое основание,
поэтому структуру любой иерархической системы можно представить в виде числа в
некоторой иерархической позиционной системе. Из дальнейшего изложения станет,
например, ясно, что Периодическая система химических элементов может быть
описана в терминах иерархической позиционной системы счисления. В терминах
позиционных иерархических систем могут быть описаны и спектры атомов химических
элементов, т.к. они непосредственно отражают структуру этих атомов. Вполне
возможно, что в некоторых разделах математики оперирование с такими числами
окажется намного “естественней”, чем в любой другой позиционной системе. В
частности, исследование подобных систем счисления может вызвать к жизни
разработку специальных вычислительных систем с иерархическим основанием системы
счисления. Например, при анализе различных структур у нас будет естественный
механизм для их идентификации и сравнения друг с другом, механизм, в котором
классификаторы основаны на иерархических позиционных системах счисления. Эти
классификаторы будут самыми естественными. В таких классификаторах с каждым из
его объектов будет связан определенный иерархический спектр “собственных”
значений. Каждый разряд числа, стоящего в определенной позиции, будет
естественным образом характеризовать свойства объекта из какого-либо его
подсемейства, указывать его место, «вес» и «роль» в общей иерархии, определяя
тем самым его семантику. Обозначения для чисел, их смысл и старшинство позиций
ничем не отличаются от обозначений чисел в любой “обычной” позиционной системе
счисления. Каждая такая иерархическая позиционная система имеет свой спектр,
характеризующий ее сложность (количество позиций и “вес” каждой позиции). Пусть,
например, позиционная система будем иметь спектр (1,1,1,1,…,1). Это означает,
что каждая позиция является двоичной. Поэтому любое число в этой системе
счисления является двоичным, а число позиций ограничено количеством знаков в
спектре системы счисления. Такие системы счисления характерны для вычислительных
машин с двоичной системой счисления с ограниченным числом разрядов, отводимым
для значения числа и характеризуют иерархическое пространство 0-го уровня
иерархии.
Пусть следующая, более старшая иерархическая
позиционная система имеет такой спектр (1,2,3,4,5). Это означает, что система
счисления ограничена пятью позициями. Самая младшая позиция имеет основание
системы счисления равной 6 (включая символ 0), следующая позиция – 5, а самая
старшая позиция является двоичной. Исследование подобных иерархических
позиционных систем счисления представляет самостоятельный интерес. Например,
спектр системы счисления по своей сути может служить в такой системе аналогом
натурального ряда чисел. Следующий пример использования – в вычислительных
машинах, в которых дешифровка иерархических чисел и символов в обычные
позиционные системы счисления будет производиться с помощью спектра
иерархической позиционной системы, отражающего структуру и состав позиционной
системы счисления. В иерархических позиционных системах счисления могут
возникать проблемы, связанные с принципом неопределенности, который существует
во многих разделах математики и естественных науках. Например, самый первый
вопрос, который можно задать, попав “внутрь” такой иерархической системы
счисления, это вопрос о том, какое самое большое число можно изобразить в этой
системе. А если нам понадобятся большие числа, то, заменив спектр на новый, мы
получим расширение для изображаемых чисел. Это, в частности, и будет означать
частичное разрешение принципа неопределенности в таких системах счисления.
Частичное потому, что извлечь самое внутреннее число из самой внутренней
оболочки иерархической системы счисления возможно только в том случае, если
известен к нему путь, который определяется спектром позиционной системы
счисления.
Для изображения иерархических чисел могут
использоваться разные способы. Например, мы можем иметь следующую форму записи
чисел
…Ах,
Вy, Cz
где многоточием обозначены старшие позиционные разряды
иерархических чисел
А, В, С…, а
х, у, z – основания систем счисления позиций
иерархического числа.
Иерархическая позиционная система
счисления с основанием
х, у, z может быть записана следующим образом
рис. 1.
Число различных способов представления
иерархических структур само по себе является прекрасным доказательством того,
насколько эти структуры важны в повседневной жизни. Например, оглавления книг
имеют иерархическую структуру. Причём способ, чаще всего используемый для
нумерации их разделов, является ещё одним, древовидным способом представления
иерархических структур. Такой метод часто называют десятичной системой
обозначений, по аналогии с классификационной схемой, применяемой в библиотеках.
Существует тесная связь между десятичной
системой, используемой для изображения иерархических структур и способом
обозначения переменных, снабженных индексами.
Обычно элементы - образующие структуры, могут содержать гораздо больше
структурных связей, чем их можно изобразить. Поэтому в каждом конкретном случае
необходимо решать, насколько подробно мы должны описывать элементы структуры, и
в соответствии с этим выбирать тот или иной уровень формального описания. Чтобы
принять нужное решение, необходимо рассматривать не только структуру, но и класс
операций, которые будут выполняться над элементами структуры. Другими словами,
структурное представление классификации в равной степени определяется требуемыми
от элементов функциями и присущими им свойствами. Такое выделение «функций»
наравне с «формой» в большинстве случаев является основополагающим. Существуют
много других способов представления иерархических структур. Ниже будут
рассмотрены некоторые наиболее важные способы изображения этих структур, которые
используются в самых различных приложениях. Но при любых способах изображения
между любыми соседними элементами, входящими в состав структуры, существуют
изначально двойственные связи. Именно их совокупность и образует
мультидвойственную структуру того или иного класса.
1.1. ЛИНЕЙНЫЕ СТРУКТУРЫ.
Линейные структуры являются самым простым
случаем иерархических структур, когда на каждом уровне иерархии может находиться
только одна структурная единица - элемент структуры. В этом случае мы будем
иметь упорядоченное множество, состоящее из n элементов
x1, x2, x3,…,
xn.
Структурные свойства этого множества по сути
ограничиваются лишь линейным (одномерным) относительным положением элементов, т.
е. теми условиями, что если n > 0, то x1 является первым элементом (корнем
структуры), если 1<k<n, то k-му элементу предшествует xk-1, за ним следует
элемент xk+1, элемент xn-есть последний элемент (лист) структуры. Поскольку в
иерархических структурах упорядочение элементов осуществляется в соответствии с
их структурной «сложностью», отражающей преемственность их строения, то мы будем
иметь линейные структуры вида
x1 É
x2 É
x3 É…
Éxn
Линейные структуры данного
вида будем называть восходящими.
x1 Ì
x2 Ì
x3 Ì…
Éxn.
Линейные структуры
данного вида будем
называть нисходящими линейными структурами.
1.2. ДРЕВОВИДНЫЕ СТРУКТУРЫ.
Древовидные структуры являются, видимо, одними из
самых «древних» структур, которые в течение многих веков постоянно находили и
находят множество применений (особенно генеалогические деревья). Как формально
определённый математический объект дерево впервые появилось, по-видимому, в
работах Г. Кирхгоффа, который, исследуя законы, носящие сейчас его имя,
использовал деревья для нахождения множества фундаментальных циклов в
электрической цепи. Формально можно определить дерево как конечное множество
Т,
состоящее из одного или более узлов, таких, что
- имеется один специально обозначенный узел,
называемый корнем дерева,
- остальные узлы (исключая корень)
содержатся в m і попарно не пересекающихся
множествах Т1, Т2..., Tn, каждое их
которых в свою очередь является деревом.
Деревья Т1, Т2, …, Тm называются поддеревьями данного
корня. Это определение является рекурсивным, т. е. мы определили дерево в
терминах самих же деревьев. Такое определение является более естественной
характеристикой подобных структур.
Действительно, рекурсивный характер деревьев налицо
также и в природе, поскольку почки молодого дерева вырастают в ветви, имеющие
собственные почки, которые дают новые ветви и т. д. Из определения следует, что
каждый узел дерева является корнем некоторого поддерева, которое содержится в
этом дереве. Следует также отметить, что порядок следований поддеревьев
Т1,…,Тm
имеет значение.
1.3. ИЕРАРХИЧЕСКИЕ ДРЕВОВИДНЫЕ СТРУКТУРЫ.
Это деревья, каждый узел которых, исключая корень и
листья, может содержать от одного до m поддеревьев. Будем говорить, что корень
дерева является самым старшим уровнем иерархии (нулевой уровень), совокупность
узлов, входящих в корень, образуют первый уровень иерархии, совокупность узлов,
входящих в узлы первого уровня иерархии, характеризуют её второй уровень и т.д.
Листья образуют последний, самый младший уровень иерархии.
1.3.1. СЕТЕВЫЕ СТРУКТУРЫ
Этот тип структур также имеет самое широкое применение
в различных приложениях. Эти структуры являются иерархическими (многоуровневыми)
интегрированными структурами. Для изображения сетевых структур можно
использовать также самые различные способы. Сетевая структура во многих случаях
является древовидной, но такой, в которой на самом старшем уровне иерархии
находится только один элемент (корень структуры) и на самом младшем уровне
иерархии также находится один элемент (лист структуры). В сетевой структуре
любой элемент может быть связан с любым другим элементом. Сетевые структуры
являются также наиболее важными иерархическими структурами. Так, генеалогические
деревья являются древовидными структурами только потому, что не включают женщин.
Однако если учесть, что каждый человек имеет двух родителей, то вместо
генеалогического дерева мы получили бы более общую иерархическую структуру -
сетевую. Существуют и другие, широко используемые в математике и других
приложениях, способы изображения структур. Но в то же время, исходя из отношений
мультидвойственности между элементами любой системы, всегда существует
возможность осуществить разложение системы на части и изобразить отдельные ее
компоненты, или даже всю систему, в виде двоичных деревьев.
1.3.2. ГРАФЫ
Чем сложнее система, тем выше ее уровень интеграции,
тем более сложной будет ее структура, тем чаще нам придется изображать ее в виде
сети, или графа. Такие структуры присущи в первую очередь сложным
интегрированным системам. Наиболее простым и употребительным способом
представления отношений иерархии n - го порядка является представление отношений
порядка на конечных упорядоченных множествах ориентированными графами. Чаще
всего граф задаётся множеством вершин Х и соответствия Г, показывающего,
как связаны между собой вершины. Соответствие Г называется отображением
множества Х в X, т. е. граф обозначается парой G= (X, Г).
1.4. ИЕРАРХИЧЕСКИЕ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ.
Жизнеспособность позиционных систем
счисления свидетельствует о том, что они отражают самую фундаментальную
закономерность нашего мира – его иерархию и вложенность явлений и объектов друг
в друга. В основу позиционных систем заложены ограниченные наборы символов
(чисел), которые играют роль их базисных элементов. Эти элементы строго
упорядочены. Как только мы выходим за пределы этого набора, происходит
“замыкание” системы, которое сигнализирует о том, что родился еще один новый,
более сложный элемент, с более высоким уровнем иерархии. В зависимости от того,
какое основание системы счисления принято за базисное, будет определяться и
название этой позиционной системы счисления. Если мы при каждом переходе к
новому старшему индексу позиционной системы будем по определенным правилам
менять ее основание, т. е. набор базисных символов (чисел) данного индекса, то
получим иерархическую позиционную систему счисления, частным случаем которой
будет являться любая другая позиционная система счисления. Такие иерархические
системы счисления могут быть использованы во многих разделах естествознания для
описания и классификации явлений и объектов окружающей действительности. В этом
случае число, характеризующее местоположение элемента в древовидной структуре,
будет не только количественно, но качественно оценивать ее уровень сложности.
Любое число в той или иной позиционной системе счисления можно изобразить в виде
некоторой структуры. Широкая распространенность позиционных систем отражает
фундаментальный принцип ограниченности и замкнутости отношений в реальном мире.
Но в реальном мире каждый уровень иерархии системы может иметь свое основание,
поэтому структуру любой иерархической системы можно представить в виде числа в
некоторой иерархической позиционной системе. Из дальнейшего изложения станет,
например, ясно, что Периодическая система химических элементов может быть
описана в терминах иерархической позиционной системы счисления. В терминах
позиционных иерархических систем могут быть описаны и спектры атомов химических
элементов, т.к. они непосредственно отражают структуру этих атомов. Вполне
возможно, что в некоторых разделах математики оперирование с такими числами
окажется намного “естественней”, чем в любой другой позиционной системе. В
частности, исследование подобных систем счисления может вызвать к жизни
разработку специальных вычислительных систем с иерархическим основанием системы
счисления. Например, при анализе различных структур у нас будет естественный
механизм для их идентификации и сравнения друг с другом, механизм, в котором
классификаторы основаны на иерархических позиционных системах счисления. Эти
классификаторы будут самыми естественными. В таких классификаторах с каждым из
его объектов будет связан определенный иерархический спектр “собственных”
значений. Каждый разряд числа, стоящего в определенной позиции, будет
естественным образом характеризовать свойства объекта из какого-либо его
подсемейства, указывать его место, «вес» и «роль» в общей иерархии, определяя
тем самым его семантику. Обозначения для чисел, их смысл и старшинство позиций
ничем не отличаются от обозначений чисел в любой “обычной” позиционной системе
счисления. Каждая такая иерархическая позиционная система имеет свой спектр,
характеризующий ее сложность (количество позиций и “вес” каждой позиции). Пусть,
например, позиционная система будем иметь спектр (1,1,1,1,…,1). Это означает,
что каждая позиция является двоичной. Поэтому любое число в этой системе
счисления является двоичным, а число позиций ограничено количеством знаков в
спектре системы счисления. Такие системы счисления характерны для вычислительных
машин с двоичной системой счисления с ограниченным числом разрядов, отводимым
для значения числа и характеризуют иерархическое пространство 0-го уровня
иерархии.
Пусть следующая, более старшая иерархическая
позиционная система имеет такой спектр (1,2,3,4,5). Это означает, что система
счисления ограничена пятью позициями. Самая младшая позиция имеет основание
системы счисления равной 6 (включая символ 0), следующая позиция – 5, а самая
старшая позиция является двоичной. Исследование подобных иерархических
позиционных систем счисления представляет самостоятельный интерес. Например,
спектр системы счисления по своей сути может служить в такой системе аналогом
натурального ряда чисел. Следующий пример использования – в вычислительных
машинах, в которых дешифровка иерархических чисел и символов в обычные
позиционные системы счисления будет производиться с помощью спектра
иерархической позиционной системы, отражающего структуру и состав позиционной
системы счисления. В иерархических позиционных системах счисления могут
возникать проблемы, связанные с принципом неопределенности, который существует
во многих разделах математики и естественных науках. Например, самый первый
вопрос, который можно задать, попав “внутрь” такой иерархической системы
счисления, это вопрос о том, какое самое большое число можно изобразить в этой
системе. А если нам понадобятся большие числа, то, заменив спектр на новый, мы
получим расширение для изображаемых чисел. Это, в частности, и будет означать
частичное разрешение принципа неопределенности в таких системах счисления.
Частичное потому, что извлечь самое внутреннее число из самой внутренней
оболочки иерархической системы счисления возможно только в том случае, если
известен к нему путь, который определяется спектром позиционной системы
счисления.
Для изображения иерархических чисел могут
использоваться разные способы. Например, мы можем иметь следующую форму записи
чисел
…Ах,
Вy, Cz
где многоточием обозначены старшие позиционные разряды
иерархических чисел
А, В, С…, а
х, у, z – основания систем счисления позиций
иерархического числа.
Иерархическая позиционная система
счисления с основанием
х, у, z может быть записана следующим образом
 где а, в, с - оболочки иерархической
системы счисления с соответствующим основанием x, y,z. Иерархические позиционные
системы могут быть вложенными друг в друга. Например, значение числа
где а, в, с - оболочки иерархической
системы счисления с соответствующим основанием x, y,z. Иерархические позиционные
системы могут быть вложенными друг в друга. Например, значение числа
 соответствует самому
последнему химическому
элементу Периодическрй таблицы Д.И.Менделеева.
Нижние индексы отражают основания системы счисления, а верхние
индексы соответствующие разряды иерархического позиционного числа (порядкового
номера химического элемента), приведенные к единому основанию (десятичной
системе счисления). Сумма разрядов даст нам порядковый номер химического
элемента, приведенного к единому основанию, т. е. равна 118. Если у всех чисел
будет единственный спектр оснований, то основания системы счисления
иерархической позиции можно опускать. Очевидно, что мы будем иметь в этом случае
“элементарную” иерархическую позиционную систему счисления. Наиболее близко к
иерархическим позиционным системам относятся сложные иерархические базы данных,
которые представляют собой многоуровневые деревья. В этих базах данных поиск и
извлечение какого-либо значения х из иерархического дерева базы данных
осуществляется с использованием сложных имен вида а.
в. с. … . х, где
а, в, с, … идентификаторы, используемые для обозначения узлов дерева. Если иерархическое
дерево будет достаточно сложным, то время поиска нужного значения может
оказаться очень большим, поэтому в подобных системах используются различные
оптимизационные методы. Одним из самых распространенных является метод, когда
идентификатор вершины на каждом уровне иерархии заменяется числовым значением,
которое указывает на порядковый номер этой вершины в данном уровне иерархии. Это
означает, что все вершины должны быть соответствующим образом упорядочены, в
результате мы получаем иерархическую позиционную систему счисления. Позиционные
системы счисления могут быть вложенными и развернутыми. Вложенная система
счисления приведена к единому началу координат и все собственные числа в такой
системе могут быть сведены в одно собственное значение. В развернутых системах
счисления каждой ее позиции соответствует собственное число, которое указывает
на “начало координат” следующей развернутой позиции. Используя иерархические
позиционные системы счисления, можно создать шифры, которые вообще нельзя будет
расшифровать, не зная ключа - спектра для каждого позиционного разряда и
основания - спектра всей системы в целом. Если учесть, что внутрь каждого
позиционного разряда могут быть заложены дополнительные помехи, и если
использовать этот шифр в совокупности с уже имеющимися шифрами, то шансы
разгадать такой шифр практически будут равны нулю. Далее, известно, что
существуют люди с феноменальными способностями выполнять сложные вычисления
быстрее компьютера. Но никто не может объяснить природу этого явления. Может
быть они пользуются иерархической системой счисления, даже не подозревая об
этом? А может быть описание голографических образов можно реализовать в терминах
иерархических позиционных систем счисления? Может быть в рамках теории
иерархических позиционных систем можно решить проблему, выдвинутую еще
математиком Гильбертом, о поиска метода, который позволил бы переупорядочить
вещественные числа, чтобы их множество стало вполне упорядоченным, в котором в
любой извлеченной из множества последовательности должен существовать первый
элемент.
2. ОПИСАНИЕ КОНЦЕПТУАЛЬНЫХ СТРУКТУР.
2.1. ОСНОВНЫЕ ПОНЯТИЯ И СВОЙСТВА
Для изображения иерархических структур выше был описан
формализм, который мы будем использовать и здесь. Дадим некоторые дополнительные
определения, необходимые для дальнейшего описания. Две структуры мы будем
считать эквивалентными, если они будут отличаться друг от друга только числом
вхождения символа 1. Например, Х1(У1)=Х(У) Таким образом символ 1 можно
вычеркивать из слов. Точнее, символ 1 замещается элементом, стоящим справа от
него, а самый правый символ 1 вычеркивается.
Две структуры мы будем называть противоположными
относительно друг друга, если они являются эквивалентными по числу входящих
символов и отличаются только тем, что эти символы входят в структуры в
противоположном порядке. Например, для слова
соответствует самому
последнему химическому
элементу Периодическрй таблицы Д.И.Менделеева.
Нижние индексы отражают основания системы счисления, а верхние
индексы соответствующие разряды иерархического позиционного числа (порядкового
номера химического элемента), приведенные к единому основанию (десятичной
системе счисления). Сумма разрядов даст нам порядковый номер химического
элемента, приведенного к единому основанию, т. е. равна 118. Если у всех чисел
будет единственный спектр оснований, то основания системы счисления
иерархической позиции можно опускать. Очевидно, что мы будем иметь в этом случае
“элементарную” иерархическую позиционную систему счисления. Наиболее близко к
иерархическим позиционным системам относятся сложные иерархические базы данных,
которые представляют собой многоуровневые деревья. В этих базах данных поиск и
извлечение какого-либо значения х из иерархического дерева базы данных
осуществляется с использованием сложных имен вида а.
в. с. … . х, где
а, в, с, … идентификаторы, используемые для обозначения узлов дерева. Если иерархическое
дерево будет достаточно сложным, то время поиска нужного значения может
оказаться очень большим, поэтому в подобных системах используются различные
оптимизационные методы. Одним из самых распространенных является метод, когда
идентификатор вершины на каждом уровне иерархии заменяется числовым значением,
которое указывает на порядковый номер этой вершины в данном уровне иерархии. Это
означает, что все вершины должны быть соответствующим образом упорядочены, в
результате мы получаем иерархическую позиционную систему счисления. Позиционные
системы счисления могут быть вложенными и развернутыми. Вложенная система
счисления приведена к единому началу координат и все собственные числа в такой
системе могут быть сведены в одно собственное значение. В развернутых системах
счисления каждой ее позиции соответствует собственное число, которое указывает
на “начало координат” следующей развернутой позиции. Используя иерархические
позиционные системы счисления, можно создать шифры, которые вообще нельзя будет
расшифровать, не зная ключа - спектра для каждого позиционного разряда и
основания - спектра всей системы в целом. Если учесть, что внутрь каждого
позиционного разряда могут быть заложены дополнительные помехи, и если
использовать этот шифр в совокупности с уже имеющимися шифрами, то шансы
разгадать такой шифр практически будут равны нулю. Далее, известно, что
существуют люди с феноменальными способностями выполнять сложные вычисления
быстрее компьютера. Но никто не может объяснить природу этого явления. Может
быть они пользуются иерархической системой счисления, даже не подозревая об
этом? А может быть описание голографических образов можно реализовать в терминах
иерархических позиционных систем счисления? Может быть в рамках теории
иерархических позиционных систем можно решить проблему, выдвинутую еще
математиком Гильбертом, о поиска метода, который позволил бы переупорядочить
вещественные числа, чтобы их множество стало вполне упорядоченным, в котором в
любой извлеченной из множества последовательности должен существовать первый
элемент.
2. ОПИСАНИЕ КОНЦЕПТУАЛЬНЫХ СТРУКТУР.
2.1. ОСНОВНЫЕ ПОНЯТИЯ И СВОЙСТВА
Для изображения иерархических структур выше был описан
формализм, который мы будем использовать и здесь. Дадим некоторые дополнительные
определения, необходимые для дальнейшего описания. Две структуры мы будем
считать эквивалентными, если они будут отличаться друг от друга только числом
вхождения символа 1. Например, Х1(У1)=Х(У) Таким образом символ 1 можно
вычеркивать из слов. Точнее, символ 1 замещается элементом, стоящим справа от
него, а самый правый символ 1 вычеркивается.
Две структуры мы будем называть противоположными
относительно друг друга, если они являются эквивалентными по числу входящих
символов и отличаются только тем, что эти символы входят в структуры в
противоположном порядке. Например, для слова
 противоположным словом будем считать
противоположным словом будем считать
 Стрелки “
Стрелки “ ” и “ ” и “ ” обозначают соответственно отношения
в слове с положительным или отрицательным градиентом сложности структурных
отношений.
Условимся рассматривать пока слова, не
содержащие символа системы S. Тогда множество слов, составленных из исходных
символов одной системы, является счётным. Следовательно, это множество можно
перенумеровать. Перенумеруем эти слова в порядке вхождений в них символов
элементов X, У, ...Теперь можно ввести понятие многочлена. Положим
aк= <0,0,0, ...,1,0,...,0>
где к-й элемент отличен от нуля и определяет
“сложность” отношения субординации для к-го слова (по его местоположению в
последовательности элементов). Тогда можно записать ” обозначают соответственно отношения
в слове с положительным или отрицательным градиентом сложности структурных
отношений.
Условимся рассматривать пока слова, не
содержащие символа системы S. Тогда множество слов, составленных из исходных
символов одной системы, является счётным. Следовательно, это множество можно
перенумеровать. Перенумеруем эти слова в порядке вхождений в них символов
элементов X, У, ...Теперь можно ввести понятие многочлена. Положим
aк= <0,0,0, ...,1,0,...,0>
где к-й элемент отличен от нуля и определяет
“сложность” отношения субординации для к-го слова (по его местоположению в
последовательности элементов). Тогда можно записать
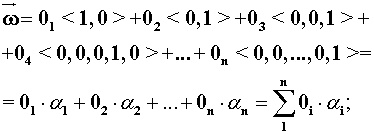 (1)
где слова
аi предполагаются равными
нулю при i>n и, следовательно, значения, принимаемые элементами многочлена,
начиная с некоторого места, равны нулю, т. е. все последующие слова являются
пустыми. Два многочлена считаются равными, если они состоят из одних и тех же
слов, и противоположными, если они записаны в противоположном порядке. Например,
многочлен, противоположный приведенному выше, будем записывать так:
(1)
где слова
аi предполагаются равными
нулю при i>n и, следовательно, значения, принимаемые элементами многочлена,
начиная с некоторого места, равны нулю, т. е. все последующие слова являются
пустыми. Два многочлена считаются равными, если они состоят из одних и тех же
слов, и противоположными, если они записаны в противоположном порядке. Например,
многочлен, противоположный приведенному выше, будем записывать так:
 (2)
Введем в множество многочленов операцию
сложения, определяемую формулами: (2)
Введем в множество многочленов операцию
сложения, определяемую формулами:
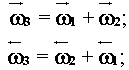 (3)
Эта операция коммутативна, ассоциативна и
обладает нейтральным элементом
(3)
Эта операция коммутативна, ассоциативна и
обладает нейтральным элементом
 ,
таким, что ,
таким, что
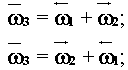 Тогда мы получим
Тогда мы получим
 Откуда непосредственно видно, что
Откуда непосредственно видно, что
 Полагая
x0=<1,0,…>
x1=<0,1,0,…>
x2=<0,0,1,0,…>
(4)
…..
xn=<0,0,....…,1>
можно определить многочлен с одной «переменной»
х
Полагая
x0=<1,0,…>
x1=<0,1,0,…>
x2=<0,0,1,0,…>
(4)
…..
xn=<0,0,....…,1>
можно определить многочлен с одной «переменной»
х
 (5)
И
мы выходим на бинарный ряд, порождающий Русскую матрицу (Русская
матрица).
В общем случае можно определить и произведение
структурных многочленов.
В
[1]
и [2] было
показано, что
произведение структурных многочленов
(5)
И
мы выходим на бинарный ряд, порождающий Русскую матрицу (Русская
матрица).
В общем случае можно определить и произведение
структурных многочленов.
В
[1]
и [2] было
показано, что
произведение структурных многочленов
 порождает новый многочлен, свойства которого можно описать следующей матрицей
размерности
порождает новый многочлен, свойства которого можно описать следующей матрицей
размерности
 . .
| |
a0a0 |
a1a1 |
a2a2 |
a3a3 |
|
a0b0 |
a0(a0b0) |
a0(a1b0) |
a0(a2b0) |
a0(a3b0) |
|
a1b1 |
a1(a0b1) |
a1(a1b1) |
a1(a2b1) |
a1(a3b1) |
|
a2b2 |
a2(a0b2) |
a2(a1b2) |
a2(a2b2) |
a2(a3b2) |
|
a3b3 |
a3(a0b3) |
a3(a1b3) |
a3(a2b3) |
a3(a3b3) |
Из таблицы видно, что для вычисления коэффициентов произведения
достаточно взять сумму соответствующих диагональных элементов
матрицы.
Эта сумма характеризуется одним и
тем же значением коэффициента и отражает отношения координации между элементами
с одним и тем же уровнем иерархии. Подчеркнём, что коэффициент
аi выражает
«сложность» отношений субординации элементов, расположенных на данном уровне. В
явном виде эти отношения субординации между элементами многочленов мы будем
выделять круглыми скобками, опуская при этом символ операции умножения
(рис. 1).
Отметим, что для структурных многочленов важен порядок
сомножителей, т. к. умножение многочленов не ассоциативно, и не коммутативно, т.е. перестановка сомножителей местами порождает
противоположный структурный многочлен. Отметим, что использование круглых скобок
и формальное преобразование структурных многочленов позволяет получать большие
преимущества при исследовании структуры системы, ибо позволяет формально
осуществлять декомпозицию системы.
Особо отметим структурные многочлены вида
 Подобные структуры мы будем называть
замкнутыми. В замкнутых структурах отношения субординации
расщепляется на два потока. Это и есть разновидность своего рода
сингулярная точка бифуркации, которая может раздваиваться на два эволюционных
потока.
Один поток обслуживает связи сверху – вниз
(директивные), другой снизу – вверх (исполнительные). Введённый таким образом
формализм может служить основой для представления иерархических структур во
многих приложениях. Выше мы условились считать, что элементы, расположенные на
разных уровнях иерархии и связанные между собой операцией умножения,
находятся между собой в отношениях субординации, т. е. между такими элементами
существуют отношения подчиненности. Элементы, расположенные на одном и том же
уровне иерархии, и связанные операцией сложения, находятся между собой в
отношениях координации. Заметим, что в сложных многоуровневых системах на одном
и том же уровне иерархии могут находиться и элементы с отношениями субординации.
В этом случае данный уровень иерархии «расщепляется” на подуровни, число которых
равно арности (мах) отношения субординации между элементами этого уровня.
2.2. СТРУКТУРНЫЕ СХЕМЫ КОНЦЕПЦИЙ
Введённый таким образом формализм,
позволяет определять структурные связи системы в виде некоторого символического
многочлена, который можно представить в виде структурной схемы (рис.
1).
Например,
многочлены
Подобные структуры мы будем называть
замкнутыми. В замкнутых структурах отношения субординации
расщепляется на два потока. Это и есть разновидность своего рода
сингулярная точка бифуркации, которая может раздваиваться на два эволюционных
потока.
Один поток обслуживает связи сверху – вниз
(директивные), другой снизу – вверх (исполнительные). Введённый таким образом
формализм может служить основой для представления иерархических структур во
многих приложениях. Выше мы условились считать, что элементы, расположенные на
разных уровнях иерархии и связанные между собой операцией умножения,
находятся между собой в отношениях субординации, т. е. между такими элементами
существуют отношения подчиненности. Элементы, расположенные на одном и том же
уровне иерархии, и связанные операцией сложения, находятся между собой в
отношениях координации. Заметим, что в сложных многоуровневых системах на одном
и том же уровне иерархии могут находиться и элементы с отношениями субординации.
В этом случае данный уровень иерархии «расщепляется” на подуровни, число которых
равно арности (мах) отношения субординации между элементами этого уровня.
2.2. СТРУКТУРНЫЕ СХЕМЫ КОНЦЕПЦИЙ
Введённый таким образом формализм,
позволяет определять структурные связи системы в виде некоторого символического
многочлена, который можно представить в виде структурной схемы (рис.
1).
Например,
многочлены
 можно записать в виде
можно записать в виде
 где стрелки над символом указывают направления
и число ориентированных связей с низлежащими уровнями иерархии.
Подобные многочлены особенно удобны для
представления древовидных структур.
Интересно заметить, что и для этой структуры можно записать структуру ей
противоположную.
Кроме того, в общем случае, за счёт введения
«избыточных» элементов, любую более сложную структуру (например,
любую сетевую структуру) можно представить в виде
некоторой совокупности древовидных структур с отношениями координации.
где стрелки над символом указывают направления
и число ориентированных связей с низлежащими уровнями иерархии.
Подобные многочлены особенно удобны для
представления древовидных структур.
Интересно заметить, что и для этой структуры можно записать структуру ей
противоположную.
Кроме того, в общем случае, за счёт введения
«избыточных» элементов, любую более сложную структуру (например,
любую сетевую структуру) можно представить в виде
некоторой совокупности древовидных структур с отношениями координации.
 рис.2
На рис.
2b показано, как структуру можно представить в виде
эквивалентной древовидной структуры.
При
этом заметьте, что попытка записать структуру
(рис.
2a)
в виде структурного многочлена привела к
порождению избыточной структуры, изображенной на рис 2b.
Свойства избыточности отражают важнейшие фундаментальные свойства
биномиальных производящих функций. Они позволяют структуры вида
1-2-4-8,
преобразовывать в структуры
1-2-3-4. Здесь число
определяет число элементов структуры на каждом уровне иерархии.
Введение избыточных элементов может служить
свидетельством того, что данные избыточные элементы, находящиеся в отношениях
координации, интегрированы между собой, между ними имеется дополнительная связь
и связанная с этой связью дополнительная функция.
Вводя избыточные элементы,
древовидную структуру можно изобразить в виде упорядоченной суммы иерархических
древовидных подструктур. Число различных способов представления древовидных
структур само по себе является доказательством того, насколько эти структуры
важны в повседневной жизни.
Рис. 2 характеризует важнейшие свойства
интегрированных друг с другом структур. Разложение такой интегрированной
структуры в ряд позволяет выделить составляющие ее подструктуры и определить на
каждом уровне иерархии степень полезности для единой структуры каждой ветви.
Абсолютная степень полезности будет определяться,
например, числом вхождений (связей)
в единую структуру одноименных ветвей. Вводя на каждом уровне для каждой ветви
ее относительный вес, мы получим количественное значение полезности этой ветви
на данном уровне иерархии (относительная полезность). Отметим лишь, что всякая
классификационная схема принимает в конце концов вид дерева.
Определим
аддитивную операцию “+” и мультипликативную операцию “*”. Будем считать, что
если два персонажа Х и У не взаимодействуют между собой, то их концепции связаны
между собой аддитивной операцией “+”. В противном случае эти концепции связаны
мультипликативной операцией “*”. В этом случае мы и имеем возможность
непосредственно использовать полученные выше многочлены для изображения
концептуальных структур. Пусть мы имеем следующий оператор
концептуализации
рис.2
На рис.
2b показано, как структуру можно представить в виде
эквивалентной древовидной структуры.
При
этом заметьте, что попытка записать структуру
(рис.
2a)
в виде структурного многочлена привела к
порождению избыточной структуры, изображенной на рис 2b.
Свойства избыточности отражают важнейшие фундаментальные свойства
биномиальных производящих функций. Они позволяют структуры вида
1-2-4-8,
преобразовывать в структуры
1-2-3-4. Здесь число
определяет число элементов структуры на каждом уровне иерархии.
Введение избыточных элементов может служить
свидетельством того, что данные избыточные элементы, находящиеся в отношениях
координации, интегрированы между собой, между ними имеется дополнительная связь
и связанная с этой связью дополнительная функция.
Вводя избыточные элементы,
древовидную структуру можно изобразить в виде упорядоченной суммы иерархических
древовидных подструктур. Число различных способов представления древовидных
структур само по себе является доказательством того, насколько эти структуры
важны в повседневной жизни.
Рис. 2 характеризует важнейшие свойства
интегрированных друг с другом структур. Разложение такой интегрированной
структуры в ряд позволяет выделить составляющие ее подструктуры и определить на
каждом уровне иерархии степень полезности для единой структуры каждой ветви.
Абсолютная степень полезности будет определяться,
например, числом вхождений (связей)
в единую структуру одноименных ветвей. Вводя на каждом уровне для каждой ветви
ее относительный вес, мы получим количественное значение полезности этой ветви
на данном уровне иерархии (относительная полезность). Отметим лишь, что всякая
классификационная схема принимает в конце концов вид дерева.
Определим
аддитивную операцию “+” и мультипликативную операцию “*”. Будем считать, что
если два персонажа Х и У не взаимодействуют между собой, то их концепции связаны
между собой аддитивной операцией “+”. В противном случае эти концепции связаны
мультипликативной операцией “*”. В этом случае мы и имеем возможность
непосредственно использовать полученные выше многочлены для изображения
концептуальных структур. Пусть мы имеем следующий оператор
концептуализации
 Тогда многочлен
Тогда многочлен
 можно изобразить в виде следующей структурной схемы
можно изобразить в виде следующей структурной схемы
 рис.
3
Повторная концептуализация дает многочлен
рис.
3
Повторная концептуализация дает многочлен
 Несмотря на более сложную структуру, схема на всех уровнях иерархии
содержит в себе одну и ту же базовую структуру (рис. 3).
Несмотря на более сложную структуру, схема на всех уровнях иерархии
содержит в себе одну и ту же базовую структуру (рис. 3).
 рис.
4
Особенность этих
структурных схем заключается прежде всего в том, что они отражают важное
свойство операторов концептуализации (Концепции), которое заключается в том, что сколько бы
раз мы ни производили концептуализаций, внутренняя организация концепции
персонажей остается неизменной, инвариантной относительно оператора
w, хотя
сложность каждого элемента структуры возрастает.
Однако возрастание этой
сложности происходит таким образом, что каждый элемент структуры содержит в себе
одну или несколько более элементарных структурных схем.
Происходит расщепление
уровней иерархии на подуровни. Подуровни в свою очередь могут иметь еще более
тонкую структуру расщепления и т. д. В результате мы получаем вложенные друг в
друга упорядоченные совокупности подструктур (оболочек
и подоболочек).
Другими словами, можно сказать,
что все подобные подструктуры будут между собой подобны.
Анализ схем,
приведенных выше, показывает, что в результате концептуализации происходит
перестройка оболочек структурной схемы таким образом, что элементы с одним и тем
же числом вхождений символов персонажей, находятся на одном и том же уровне
иерархии и объединяются в оболочки (и подоболочки).
Так для схемы (рис. 4) мы имеем два уровня
иерархии, соответственно две оболочки
рис.
4
Особенность этих
структурных схем заключается прежде всего в том, что они отражают важное
свойство операторов концептуализации (Концепции), которое заключается в том, что сколько бы
раз мы ни производили концептуализаций, внутренняя организация концепции
персонажей остается неизменной, инвариантной относительно оператора
w, хотя
сложность каждого элемента структуры возрастает.
Однако возрастание этой
сложности происходит таким образом, что каждый элемент структуры содержит в себе
одну или несколько более элементарных структурных схем.
Происходит расщепление
уровней иерархии на подуровни. Подуровни в свою очередь могут иметь еще более
тонкую структуру расщепления и т. д. В результате мы получаем вложенные друг в
друга упорядоченные совокупности подструктур (оболочек
и подоболочек).
Другими словами, можно сказать,
что все подобные подструктуры будут между собой подобны.
Анализ схем,
приведенных выше, показывает, что в результате концептуализации происходит
перестройка оболочек структурной схемы таким образом, что элементы с одним и тем
же числом вхождений символов персонажей, находятся на одном и том же уровне
иерархии и объединяются в оболочки (и подоболочки).
Так для схемы (рис. 4) мы имеем два уровня
иерархии, соответственно две оболочки
 При этом каждая
из этих оболочек состоит в свою
очередь из подоболочек
При этом каждая
из этих оболочек состоит в свою
очередь из подоболочек
 3. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ КОНЦЕПТУАЛЬНЫХ
СТРУКТУР
3.1. РАСКРЫТИЕ СКОБОК.
Пусть мы имеем структурный многочлен
3. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ КОНЦЕПТУАЛЬНЫХ
СТРУКТУР
3.1. РАСКРЫТИЕ СКОБОК.
Пусть мы имеем структурный многочлен
 Тогда, полагая, что для многочлена справедлив закон
дистрибутивности, мы получим
Тогда, полагая, что для многочлена справедлив закон
дистрибутивности, мы получим
 3.2. ВЫНЕСЕНИЕ СИМВОЛА ПЕРСОНАЖА ЗА СКОБКИ
Структурная схема для приведенного выше
многочлена имеет вид, показанный на рис. 5. слева.
3.2. ВЫНЕСЕНИЕ СИМВОЛА ПЕРСОНАЖА ЗА СКОБКИ
Структурная схема для приведенного выше
многочлена имеет вид, показанный на рис. 5. слева.
 рис. 5.
Вынесем за внешние скобки символ персонажа Х. Тогда мы
получим многочлен, структурная схема которого будет иметь вид (рис.
5. справа).
Мы получили для данного структурного многочлена
компактную форму записи. Дальнейшее «сжатие» структуры в рамках данного
представления уже является невозможным.
Отметим, что символ «1» в структурных
многочленах означает объединение частей структуры в целое
и означает, что в
дальнейшем этот символ может замещаться каким-либо символом персонажа системы.
3.3. УМНОЖЕНИЕ СТРУКТУРНЫХ МНОГОЧЛЕНОВ
Если
рис. 5.
Вынесем за внешние скобки символ персонажа Х. Тогда мы
получим многочлен, структурная схема которого будет иметь вид (рис.
5. справа).
Мы получили для данного структурного многочлена
компактную форму записи. Дальнейшее «сжатие» структуры в рамках данного
представления уже является невозможным.
Отметим, что символ «1» в структурных
многочленах означает объединение частей структуры в целое
и означает, что в
дальнейшем этот символ может замещаться каким-либо символом персонажа системы.
3.3. УМНОЖЕНИЕ СТРУКТУРНЫХ МНОГОЧЛЕНОВ
Если
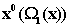 и и
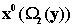 есть
структурные многочлены, то есть
структурные многочлены, то
 есть также структурный многочлен. Здесь символ
х0 =1 означает корень структурного дерева, вместо которого будет в дальнейшем записан
некоторый символ персонажа и, тем самым, будет осуществляться преобразование
дерева в некоторое новое поддерево.
Умножение многочленов даёт
есть также структурный многочлен. Здесь символ
х0 =1 означает корень структурного дерева, вместо которого будет в дальнейшем записан
некоторый символ персонажа и, тем самым, будет осуществляться преобразование
дерева в некоторое новое поддерево.
Умножение многочленов даёт
 Пусть
Пусть
 ,
а ,
а  Тогда
Тогда
 Для данного многочлена будет справедлива
следующая интерпретация. Сомножители, стоящие в левой части отражают «сжатую»
иерархическую структуру многочлена, в которой второй сомножитель является
базисным элементом структуры (листом дерева).
Количество сомножителей
характеризует число уровней иерархии структуры, а структура каждого сомножителя
характеризует структуру соответствующего уровня иерархии. Выражение, стоящее в
правой части, отражает фактическую структурную сложность каждого элемента на
самом элементарном уровне иерархии структуры.
3.4. СЛОЖЕНИЕ СТРУКТУРНЫХ МНОГОЧЛЕНОВ
Если
Для данного многочлена будет справедлива
следующая интерпретация. Сомножители, стоящие в левой части отражают «сжатую»
иерархическую структуру многочлена, в которой второй сомножитель является
базисным элементом структуры (листом дерева).
Количество сомножителей
характеризует число уровней иерархии структуры, а структура каждого сомножителя
характеризует структуру соответствующего уровня иерархии. Выражение, стоящее в
правой части, отражает фактическую структурную сложность каждого элемента на
самом элементарном уровне иерархии структуры.
3.4. СЛОЖЕНИЕ СТРУКТУРНЫХ МНОГОЧЛЕНОВ
Если  и и
 -структурные
многочлены, то -структурные
многочлены, то
 также структурный многочлен, представляющий собой
децентрализованную структуру с максимальной сложностью отношений субординации в
модулях, её составляющих (
также структурный многочлен, представляющий собой
децентрализованную структуру с максимальной сложностью отношений субординации в
модулях, её составляющих ( и и
 ).
3.5. СДВИГ СТРУКТУРНОГО МНОГОЧЛЕНА
Это частный случай умножения структурных многочленов. Если ).
3.5. СДВИГ СТРУКТУРНОГО МНОГОЧЛЕНА
Это частный случай умножения структурных многочленов. Если
 -структурный многочлен, а -структурный многочлен, а
 - также
структурный многочлен, то в результате умножения получим
- также
структурный многочлен, то в результате умножения получим
 структурный многочлен, сдвинутый на n уровней иерархии
вправо (на структурной схеме - вниз), при этом “пустые” уровни иерархии
заполняются символом персонажа Х, т.е. такой многочлен можно
переписать в следующем виде
структурный многочлен, сдвинутый на n уровней иерархии
вправо (на структурной схеме - вниз), при этом “пустые” уровни иерархии
заполняются символом персонажа Х, т.е. такой многочлен можно
переписать в следующем виде
 3.6. РАЗВЁРТКА СТРУКТУРНЫХ МНОГОЧЛЕНОВ
Это
тоже частный случай умножения
структурных многочленов вида
3.6. РАЗВЁРТКА СТРУКТУРНЫХ МНОГОЧЛЕНОВ
Это
тоже частный случай умножения
структурных многочленов вида
 Тогда,
выполняя умножение, получим
Тогда,
выполняя умножение, получим
 Структурные схемы этих многочленов имеют вид .
Структурные схемы этих многочленов имеют вид .
 рис.
6.
Последняя структурная схема может служить хорошей
математической иллюстрацией закономерности преемственности и экспоненциального
роста структуры системы в процессе её эволюции, когда на каждом этапе система
как бы копирует саму себя и потом добавляет новую уникальную оболочку, в
соответствии с рекуррентными правилами формирования того или иного уровня
иерархии. Тот факт, что любую структуру можно представить в виде
совокупности древовидных структур за счет введения избыточных элементов,
означает, что мы имеем дело с многофункциональными элементами, что мы таким
образом имеем возможность выделить эти отдельные функции элемента, обособить их
в рамках отдельной древовидной структуры, которая будет служить для достижения
системой одной из ее функций. Использование структурных многочленов может быть
полезно и для других классов структур, а не только древовидных. Для этого можно
только ввести некоторые дополнительные операции, или модернизируя операции,
введенные выше.
3.7. СВЕРТКА СТРУКТУРНЫХ МНОГОЧЛЕНОВ
В результате свертки структурный многочлен
преобразуется таким образом, что по своей структуре будет тождественен к
исходному концептуальному многочлену. Процесс свертки заключается в том, что
происходит преобразование структуры к более простому виду.
Пусть, например, мы имеем следующие структурные
многочлены
рис.
6.
Последняя структурная схема может служить хорошей
математической иллюстрацией закономерности преемственности и экспоненциального
роста структуры системы в процессе её эволюции, когда на каждом этапе система
как бы копирует саму себя и потом добавляет новую уникальную оболочку, в
соответствии с рекуррентными правилами формирования того или иного уровня
иерархии. Тот факт, что любую структуру можно представить в виде
совокупности древовидных структур за счет введения избыточных элементов,
означает, что мы имеем дело с многофункциональными элементами, что мы таким
образом имеем возможность выделить эти отдельные функции элемента, обособить их
в рамках отдельной древовидной структуры, которая будет служить для достижения
системой одной из ее функций. Использование структурных многочленов может быть
полезно и для других классов структур, а не только древовидных. Для этого можно
только ввести некоторые дополнительные операции, или модернизируя операции,
введенные выше.
3.7. СВЕРТКА СТРУКТУРНЫХ МНОГОЧЛЕНОВ
В результате свертки структурный многочлен
преобразуется таким образом, что по своей структуре будет тождественен к
исходному концептуальному многочлену. Процесс свертки заключается в том, что
происходит преобразование структуры к более простому виду.
Пусть, например, мы имеем следующие структурные
многочлены
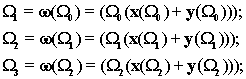 Здесь каждый последующий многочлен
является сверткой предыдущего, т.е. каждый предыдущий многочлен в таких
структурах играет роль элементарного члена структуры (базисный элемент).
Используя метод подстановки, все эти многочлены можно развернуть, выражая многочлен
Wi
через
W1.
4. О СТРУКТУРНОМ ПРОГРАММИРОВАНИИ
4.1.
О СУЩНОСТИ СТРУКТУРНОГО ПРОГРАММИРОВАНИЯ
Одним из ярчайших примеров торжества идей
законов иерархии может служить эволюция вычислительной техники и, в первую
очередь, программного обеспечения компьютеров.
Программное обеспечение компьютеров
появилось позднее аппаратного. По мере увеличения сложности аппаратуры
возрастали и возможности программного обеспечения. Были созданы ассемблеры,
компиляторы, операционные системы и системы управления базами данных.
Хотя в основе ряда дисциплин, смежных с вычислительной техникой, например,
математической логики, лингвистики, теории автоматов и др., лежит математика, у
большинства специалистов до сих пор был и остается подход к разработке
программного обеспечения скорее прагматический, нежели теоретический. А между
тем эволюция программного обеспечения, эволюция компьютеров, со всей
очевидностью свидетельствует о том, что именно в этой сфере наиболее ярко
проявляются законы эволюции, законы иерархии. Предшествующее поколение
программистов обучалось программированию непосредственно программированием.
Программисты мыслили абстрактными категориями (машинными двоичными кодами).
Пользователь получал результат, не зная ход (пути) решения задачи. Выход из
тупика вначале был найден на пути структурного (модульного) программирования,
при котором задача расчленялась на блоки (модули), из которых потом складывалась
та или иная программа. Формировались библиотеки стандартных программ, из
которых, как из кирпичиков, строились другие программы. Здесь уже начал
возникать совершенно новый механизм (в программировании, но не в математике и
др. науках), при котором на некоторый стандартный набор кирпичиков отражалось
бесконечное число пространственных “образов”. Последовательное прохождение
дерева конкретного “образа” программы, с использованием некоторого набора
конкретных базисных элементов, приводило к получению конкретного результата. В
программировании стал развиваться естественный механизм, который по своим
возможностям можно сравнить, пожалуй, только с мозгом человека. Структурное
программирование явилось прообразом “образного мышления” компьютера, которое
постоянно совершенствуется. При этом одни и те же кирпичики могли использоваться
многократно, не только в рамках одного образа, но и при создании других
компьютерных образов. Сами же кирпичики являлись листьями конкретных “образов”.
При этом, чем сложнее сеть деревьев с образами, тем сильнее будут возможности
находить и определять “аналогичные” образы, тем больше у компьютера будет
“интеллектуальных” возможностей. Дальнейшая эволюция подтвердила стратегическую
линию на развитие этих возможностей. В качестве кирпичиков стали использовать
сами данные. При этом чем больше накапливалось данных, тем острее становилась
проблема управления этими данными. Поэтому возникли хранилища данных, с
механизмами их контроля и управления, которые стали называть базами данных.
Программное обеспечение и базы данных все
более и более стали напоминать мозг человека. Действительно, здесь есть полная
аналогия. В одном “полушарии” компьютера хранятся листья образов (программы и
данные), а в другом – сами образы, которые представляют собой многоуровневые
цепочки произвольной длины, имеющие многочисленные зацикливания. При прохождении
дерева образа в строго определенном порядке возникает “пространственный”
объект-оригинал образа. Этот процесс может быть многоуровневым, многослойным.
Составляя цепочки из кирпичиков, каждый из которых будет деревом образов, мы
получим более сложное дерево, получим более сложный образ и т. д. Эта
двойственная совокупность цепочек и кирпичиков будет составлять первый уровень
иерархии системы, первый слой ее оболочек. Если теперь в качестве кирпичиков
использовать образную часть оболочки и начать формировать из этого набора
различные образы, то мы получим следующий двойственный слой системы и т. д. В
принципе, именно по такому образу и подобию функционируют все иерархические
системы. Поэтому можно сказать, что программирование является процессом
спектрального разложения образа объекта на две составляющие, из которых первая
связывает в строго определенном порядке все элементарные кирпичики образа, а
сами кирпичики размещает во втором “полушарии”. Можно сказать, что одно
полушарие компьютера отвечает за образное мышление, другое – за абстрактное, так
как содержит только первичные данные. Это полушарие составляет самый низкий
уровень “интеллекта” компьютера. Полушарие, отвечающее за образное мышление,
естественно, составляет более высокий уровень интеллекта компьютера.
Таким образом, прогресс в вычислительной
технике обязан, прежде всего, тому, что человек, не зная об этом, скопировал у
природы самый оптимальный способ организации иерархических систем.
Во-первых, это увязывание всех элементов в
единую целостную многоуровневую систему.
Во-вторых, это последовательный, строго
эволюционный характер создания все более сложных иерархических систем.
В-третьих, это двойственный характер всех
программных оболочек и подоболочек, их ограниченность и замкнутость, наличие
прямых и обратных связей, и т. д. и т. п.
В-четвертых, интеграционный характер
совершенствования баз данных, в результате которого и формируется искусственный
интеллект компьютера. Процесс создания искусственного интеллекта можно пояснить
следующим образом. В процессе интеграции иерархических структур, характеризующих
конкретное решение какой-либо задачи (создание проекта, поиска информации,
анализ структур и т.д.) эти частные структурные поддеревья накладываются друг на
друга, формируя единую структуру, в которой каждая ветвь на каждом уровне
иерархии единой структуры может иметь разное число вхождений в единую структуру
и тем самым создавая естественный механизм нормирования этих ветвей по степени
их «полезности» в единой структуре. Поэтому у Природы (у компьютера) для каждого
уровня иерархии единой структуры имеется естественный механизм формального
определения полезности (веса) каждой структурной ветви в относительных единицах.
В результате процессов интеграции структурных поддеревьев в единое структурное
дерево, ранжирования ветвей единой структуры по степени их полезности
формируется такое понятие, как интуиция компьютера, интуиция искусственного
Разума. Действительно, в этом случае при решении любой интеллектуальной задачи
достаточно на каждом уровне иерархии выбирать вершину (ветвь), имеющую
максимальный уровень полезности в структуре (задача максимизации полезности при
определенном наборе двойственных ограничений целевой функции - типичная задача
линейного программирования). Дальнейшая эволюция вычислительной техники будет
связана с созданием принципиально нового компьютера, который будет способен
копировать, воспроизводить и “мыслить” пространственными образами, точно так,
как это делает человек. В принципе, эти успехи человека не являются новыми для
программирования. Эти идеи изначально составляют основу лингвистики и служат для
описания синтаксиса и семантики как естественных языков, так и языков, созданных
исключительно для нужд программирования.
4.2.
О РОЛЕВЫХ СТРУКТУРНЫХ МНОГОЧЛЕНАХ
О сущности ролевых структурных многочленов можно получить на странице "Концепции",
на которой даются первые представления о концептуальных многочленах.
Концептуальные многочлены могут нести в себе самые разнообразные смыслы
(замыслы), которые могут отображаться с использованием одной и той же концепции,
формируемой с использованием соответствующего оператора концептуализации,
порождающего для исходного замысла соответствующий класс структурных
многочленов.
Замысел концепции может отражать разные системные грани одной и той же системы.
Он отражает разные условия функционирования системы в зависимости от
изменений внешней среды.
Можно говорить о том, что система, используя определенный набор
"замыслов" функционирования. приобретает возможность адаптации к условиям
жизнедеятельности. Применительно к человеку такие наборы "замыслов" называют
обычно ролями.
Каждый человек может играть множество ролей:
на работе дома,
на отдыхе, и т.д. И человек от этого не становится многоликим Янусом. Он
остается самим собой.
Но вот
когда мы говорим о системах, об их способности к адаптации к внешней среде, мы
забываем об этой элементарной истине. Поэтому использование концептуальных
многочленов может дать важные преимущества в исследовании систем. Ибо определив
исходный оператор концептуализации, мы тем самым можем сформировать
соответствующий класс структурных многочленов, отражающих ту или иную"роль"
системы.
На странице "Ролевая концепция"
было обосновано использование ролевой монады применительно к менеджменту. Эта
концепция самым естественным образом интегрирует все существующие теории
менеджмента в единую стройную теорию
ролевого менеджмента.
Ролевая монада отражает в себе Замысел и Цель
эволюции. Это монада "Ян-Инь", развернутая в Куб закона.
Здесь каждый последующий многочлен
является сверткой предыдущего, т.е. каждый предыдущий многочлен в таких
структурах играет роль элементарного члена структуры (базисный элемент).
Используя метод подстановки, все эти многочлены можно развернуть, выражая многочлен
Wi
через
W1.
4. О СТРУКТУРНОМ ПРОГРАММИРОВАНИИ
4.1.
О СУЩНОСТИ СТРУКТУРНОГО ПРОГРАММИРОВАНИЯ
Одним из ярчайших примеров торжества идей
законов иерархии может служить эволюция вычислительной техники и, в первую
очередь, программного обеспечения компьютеров.
Программное обеспечение компьютеров
появилось позднее аппаратного. По мере увеличения сложности аппаратуры
возрастали и возможности программного обеспечения. Были созданы ассемблеры,
компиляторы, операционные системы и системы управления базами данных.
Хотя в основе ряда дисциплин, смежных с вычислительной техникой, например,
математической логики, лингвистики, теории автоматов и др., лежит математика, у
большинства специалистов до сих пор был и остается подход к разработке
программного обеспечения скорее прагматический, нежели теоретический. А между
тем эволюция программного обеспечения, эволюция компьютеров, со всей
очевидностью свидетельствует о том, что именно в этой сфере наиболее ярко
проявляются законы эволюции, законы иерархии. Предшествующее поколение
программистов обучалось программированию непосредственно программированием.
Программисты мыслили абстрактными категориями (машинными двоичными кодами).
Пользователь получал результат, не зная ход (пути) решения задачи. Выход из
тупика вначале был найден на пути структурного (модульного) программирования,
при котором задача расчленялась на блоки (модули), из которых потом складывалась
та или иная программа. Формировались библиотеки стандартных программ, из
которых, как из кирпичиков, строились другие программы. Здесь уже начал
возникать совершенно новый механизм (в программировании, но не в математике и
др. науках), при котором на некоторый стандартный набор кирпичиков отражалось
бесконечное число пространственных “образов”. Последовательное прохождение
дерева конкретного “образа” программы, с использованием некоторого набора
конкретных базисных элементов, приводило к получению конкретного результата. В
программировании стал развиваться естественный механизм, который по своим
возможностям можно сравнить, пожалуй, только с мозгом человека. Структурное
программирование явилось прообразом “образного мышления” компьютера, которое
постоянно совершенствуется. При этом одни и те же кирпичики могли использоваться
многократно, не только в рамках одного образа, но и при создании других
компьютерных образов. Сами же кирпичики являлись листьями конкретных “образов”.
При этом, чем сложнее сеть деревьев с образами, тем сильнее будут возможности
находить и определять “аналогичные” образы, тем больше у компьютера будет
“интеллектуальных” возможностей. Дальнейшая эволюция подтвердила стратегическую
линию на развитие этих возможностей. В качестве кирпичиков стали использовать
сами данные. При этом чем больше накапливалось данных, тем острее становилась
проблема управления этими данными. Поэтому возникли хранилища данных, с
механизмами их контроля и управления, которые стали называть базами данных.
Программное обеспечение и базы данных все
более и более стали напоминать мозг человека. Действительно, здесь есть полная
аналогия. В одном “полушарии” компьютера хранятся листья образов (программы и
данные), а в другом – сами образы, которые представляют собой многоуровневые
цепочки произвольной длины, имеющие многочисленные зацикливания. При прохождении
дерева образа в строго определенном порядке возникает “пространственный”
объект-оригинал образа. Этот процесс может быть многоуровневым, многослойным.
Составляя цепочки из кирпичиков, каждый из которых будет деревом образов, мы
получим более сложное дерево, получим более сложный образ и т. д. Эта
двойственная совокупность цепочек и кирпичиков будет составлять первый уровень
иерархии системы, первый слой ее оболочек. Если теперь в качестве кирпичиков
использовать образную часть оболочки и начать формировать из этого набора
различные образы, то мы получим следующий двойственный слой системы и т. д. В
принципе, именно по такому образу и подобию функционируют все иерархические
системы. Поэтому можно сказать, что программирование является процессом
спектрального разложения образа объекта на две составляющие, из которых первая
связывает в строго определенном порядке все элементарные кирпичики образа, а
сами кирпичики размещает во втором “полушарии”. Можно сказать, что одно
полушарие компьютера отвечает за образное мышление, другое – за абстрактное, так
как содержит только первичные данные. Это полушарие составляет самый низкий
уровень “интеллекта” компьютера. Полушарие, отвечающее за образное мышление,
естественно, составляет более высокий уровень интеллекта компьютера.
Таким образом, прогресс в вычислительной
технике обязан, прежде всего, тому, что человек, не зная об этом, скопировал у
природы самый оптимальный способ организации иерархических систем.
Во-первых, это увязывание всех элементов в
единую целостную многоуровневую систему.
Во-вторых, это последовательный, строго
эволюционный характер создания все более сложных иерархических систем.
В-третьих, это двойственный характер всех
программных оболочек и подоболочек, их ограниченность и замкнутость, наличие
прямых и обратных связей, и т. д. и т. п.
В-четвертых, интеграционный характер
совершенствования баз данных, в результате которого и формируется искусственный
интеллект компьютера. Процесс создания искусственного интеллекта можно пояснить
следующим образом. В процессе интеграции иерархических структур, характеризующих
конкретное решение какой-либо задачи (создание проекта, поиска информации,
анализ структур и т.д.) эти частные структурные поддеревья накладываются друг на
друга, формируя единую структуру, в которой каждая ветвь на каждом уровне
иерархии единой структуры может иметь разное число вхождений в единую структуру
и тем самым создавая естественный механизм нормирования этих ветвей по степени
их «полезности» в единой структуре. Поэтому у Природы (у компьютера) для каждого
уровня иерархии единой структуры имеется естественный механизм формального
определения полезности (веса) каждой структурной ветви в относительных единицах.
В результате процессов интеграции структурных поддеревьев в единое структурное
дерево, ранжирования ветвей единой структуры по степени их полезности
формируется такое понятие, как интуиция компьютера, интуиция искусственного
Разума. Действительно, в этом случае при решении любой интеллектуальной задачи
достаточно на каждом уровне иерархии выбирать вершину (ветвь), имеющую
максимальный уровень полезности в структуре (задача максимизации полезности при
определенном наборе двойственных ограничений целевой функции - типичная задача
линейного программирования). Дальнейшая эволюция вычислительной техники будет
связана с созданием принципиально нового компьютера, который будет способен
копировать, воспроизводить и “мыслить” пространственными образами, точно так,
как это делает человек. В принципе, эти успехи человека не являются новыми для
программирования. Эти идеи изначально составляют основу лингвистики и служат для
описания синтаксиса и семантики как естественных языков, так и языков, созданных
исключительно для нужд программирования.
4.2.
О РОЛЕВЫХ СТРУКТУРНЫХ МНОГОЧЛЕНАХ
О сущности ролевых структурных многочленов можно получить на странице "Концепции",
на которой даются первые представления о концептуальных многочленах.
Концептуальные многочлены могут нести в себе самые разнообразные смыслы
(замыслы), которые могут отображаться с использованием одной и той же концепции,
формируемой с использованием соответствующего оператора концептуализации,
порождающего для исходного замысла соответствующий класс структурных
многочленов.
Замысел концепции может отражать разные системные грани одной и той же системы.
Он отражает разные условия функционирования системы в зависимости от
изменений внешней среды.
Можно говорить о том, что система, используя определенный набор
"замыслов" функционирования. приобретает возможность адаптации к условиям
жизнедеятельности. Применительно к человеку такие наборы "замыслов" называют
обычно ролями.
Каждый человек может играть множество ролей:
на работе дома,
на отдыхе, и т.д. И человек от этого не становится многоликим Янусом. Он
остается самим собой.
Но вот
когда мы говорим о системах, об их способности к адаптации к внешней среде, мы
забываем об этой элементарной истине. Поэтому использование концептуальных
многочленов может дать важные преимущества в исследовании систем. Ибо определив
исходный оператор концептуализации, мы тем самым можем сформировать
соответствующий класс структурных многочленов, отражающих ту или иную"роль"
системы.
На странице "Ролевая концепция"
было обосновано использование ролевой монады применительно к менеджменту. Эта
концепция самым естественным образом интегрирует все существующие теории
менеджмента в единую стройную теорию
ролевого менеджмента.
Ролевая монада отражает в себе Замысел и Цель
эволюции. Это монада "Ян-Инь", развернутая в Куб закона.

 рис.
7
Из
рисунков видно, что Великий ТАЙ ЦЗИ порождает исходную монаду Ян-Инь,
отражающих Замысел (смысл) и Цель эволюции , т.е.
это монада "Замысел-Цель".
Теперь
эволюцию Великого предела ТАЙ ЦЗИ можно записать в виде структурного многочлена
Обозначая Замысел Великого
Предела через
W0,
а
оператор концептуализации через
w
, мы получим
следующую инвариантную запись эволюции ролевой монады
рис.
7
Из
рисунков видно, что Великий ТАЙ ЦЗИ порождает исходную монаду Ян-Инь,
отражающих Замысел (смысл) и Цель эволюции , т.е.
это монада "Замысел-Цель".
Теперь
эволюцию Великого предела ТАЙ ЦЗИ можно записать в виде структурного многочлена
Обозначая Замысел Великого
Предела через
W0,
а
оператор концептуализации через
w
, мы получим
следующую инвариантную запись эволюции ролевой монады
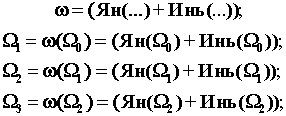 Из этой записи
непосредственно видно, что на каждом уровне иерархии используется один и
тот же оператор концептуализации и что Ян и Инь являются многоуровневыми.
Поскольку здесь отражено три
уровня, то каждая вершина третьего уровня иерархии является триграммой.
Эти
свойства особенно ярко проявляются в схеме эволюции Великого Предела ТАЙ ЦЗЫ.
Из этой записи
непосредственно видно, что на каждом уровне иерархии используется один и
тот же оператор концептуализации и что Ян и Инь являются многоуровневыми.
Поскольку здесь отражено три
уровня, то каждая вершина третьего уровня иерархии является триграммой.
Эти
свойства особенно ярко проявляются в схеме эволюции Великого Предела ТАЙ ЦЗЫ.
 рис.
8
Видите, как все тривиально просто!
Приведенные выше алгебраические формулы и их геометрическая интерпретация отражают Единый закон эволюции
двойственного отношения.
Эти формулы и являются всеобщим инвариантом эволюции
живой и неживой материи.
Рис. 5 несет в себе великий смысл иерархии понятия
"ТРИЕДИНСТВО".
Формула триединства
рис.
8
Видите, как все тривиально просто!
Приведенные выше алгебраические формулы и их геометрическая интерпретация отражают Единый закон эволюции
двойственного отношения.
Эти формулы и являются всеобщим инвариантом эволюции
живой и неживой материи.
Рис. 5 несет в себе великий смысл иерархии понятия
"ТРИЕДИНСТВО".
Формула триединства
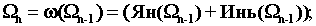 позволяет осознать одну из самых невежественных страниц человеческого мышления,
ибо она позволяет преодолеть дихотомию мышления.
Вспомните хотя бы о проблеме "яйца" и "курицы". Это монада "яйцо-курица" и в
соответствии с формулой триединства, она имеет Великий Предел, в который
может сворачиваться эта монада и из которого она может разворачиваться.
Уровни иерархии ролевой монады порождают бинарный ряд:
(1+2+4+8)=(20+21+22+23).
В общем случае, раскрывая уровни иерархии, мы можем
получать формулы вида
позволяет осознать одну из самых невежественных страниц человеческого мышления,
ибо она позволяет преодолеть дихотомию мышления.
Вспомните хотя бы о проблеме "яйца" и "курицы". Это монада "яйцо-курица" и в
соответствии с формулой триединства, она имеет Великий Предел, в который
может сворачиваться эта монада и из которого она может разворачиваться.
Уровни иерархии ролевой монады порождают бинарный ряд:
(1+2+4+8)=(20+21+22+23).
В общем случае, раскрывая уровни иерархии, мы можем
получать формулы вида
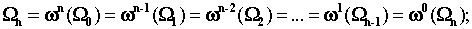 На странице "Русская матрица" мы обосновали, что
в основе Русской матрицы лежит бинарный ряд
....+25+24+23+22+21+20+2-1+2-2+2-3+2-4+2-5+.....
т.е.
горизонтальная и вертикальная ось
симметрии Русской матрицы представляют собой степенной бинарный ряд вида
....+25+24+23+22+21+20+2-1+2-2+2-3+2-4+2-5+.....
умножая которые на на соответствующие члены золотого ряда
На странице "Русская матрица" мы обосновали, что
в основе Русской матрицы лежит бинарный ряд
....+25+24+23+22+21+20+2-1+2-2+2-3+2-4+2-5+.....
т.е.
горизонтальная и вертикальная ось
симметрии Русской матрицы представляют собой степенной бинарный ряд вида
....+25+24+23+22+21+20+2-1+2-2+2-3+2-4+2-5+.....
умножая которые на на соответствующие члены золотого ряда
|
Ф-4 |
Ф-3 |
Ф-2 |
Ф-1 |
Ф0 |
Ф1 |
Ф2 |
Ф3 |
Ф4 |
где Ф1=1,618.
Таким образом, алгебраическая форма записи схемы эволюции Великого Предела
(рис.5) отражает самое фундаментальное свойство Единого закона эволюции монады.
РЕЗЮМЕ
1. Структурные многочлены показывают их
важнейшие свойства - свойства инвариантности, свойства симметрии преобразований,
которые сохраняются даже при многократном применении одних и тех же
преобразований, в результате которых структура многочленов остается неизменной.
В общем случае инвариантность структурных многочленов справедлива
для всех иерархических систем, независимо от их природы и свидетельствует о том,
что концептуальные многочлены с такими свойствами могут играть роль всеобщего
инварианта.
2.
Симметрия инвариантных преобразований свидетельствует о
фундаментальных свойствах иерархических систем любой природы. Операции над структурными многочленами вскрывают их
иерархический смысл. Оказывается, что каждый структурный сомножитель можно
отождествить с определенным уровнем иерархии структуры, в которой структурная
сложность каждого уровня иерархии определяется соответствующим структурным
сомножителем.
3. Вышеизложенные идеи о структурных и
концептуальных многочленах могут иметь самостоятельное прикладное значение и могут быть
применены для структурного описания чрезвычайно сложных интегрированных
иерархических систем с использованием некоторых наиболее известных приемов,
которые широко распространены в математике и могут быть полезны для работы с
концептуальными многочленами.
4. Вводя те или иные операторы
концептуализации, мы можем
получать самые различные классы структурных многочленов для описания
концептуальных структур. Рассмотренные структурные схемы концепций наглядно
показывают сущность последовательного применения операторов концептуализации к
исходному концептуальному многочлену. Структурные схемы раскрывают вложенность
концептуальных оболочек и подоболочек друг в друга, их способность
интегрироваться друг с другом, их способность к формированию двойственных и
мультидвойственных отношений. Свертка и развертка структурных многочленов может
быть с успехом использована при решении задач создания искусственного
интеллекта.
5. Структурные многочлены и схемы могут
быть использованы и при анализе оболочек и подоболочек Периодической системы
химических элементов, ядерных оболочек и подоболочек, при анализе классификаций
элементарных частиц, а также других научных приложениях.
|



 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©





 ” и “
” и “ ” обозначают соответственно отношения
в слове с положительным или отрицательным градиентом сложности структурных
отношений.
” обозначают соответственно отношения
в слове с положительным или отрицательным градиентом сложности структурных
отношений.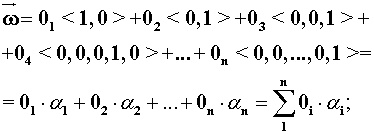

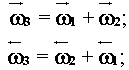
 ,
,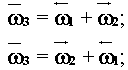



















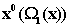 и
и 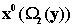


 ,
, 

 и
и
 -структурные
многочлены, то
-структурные
многочлены, то
 и
и
 ).
). -структурный многочлен, а
-структурный многочлен, а