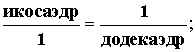О ВЫСШИХ ИЗМЕРЕНИЯХ
ЧАСТЬ
I.
1.
О МНОГОМЕРНОСТИ ПРОСТРАНСТВ
О многомерности пространств написано столько ученых книг, столько математических
теорий, что еще одной новой теорией никого не удивить. Впрочем, этого здесь и не
требуется. Важно понять, что многомерность с числом измерений более трех может
существовать в реальности. При этом не надо искать такие Вселенные где-то за
пределами нашего сознания. Такие Вселенные существуют рядом и вместе с нами.
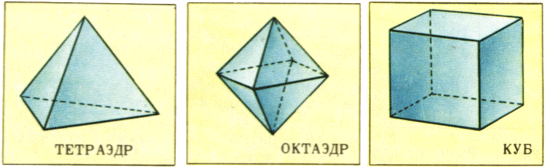
Достаточно вспомнить мир кристаллов, который складывается из Платоновых тел
(рис. 1), а
каждое Платоново тело может быть представлено как совокупность триангуляров и
корпускуляров.
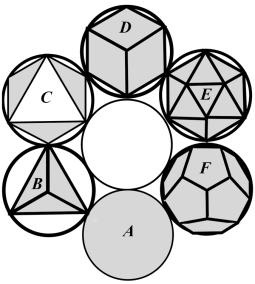 рис. 1
Эти
кристаллы можно назвать совершенными. При рассмотрении свойств монадных кристаллов мы уже рассматривали свойства
кристаллов формировать собственные пространства с числом измерений более трех. В
этих собственных пространствах монадных кристаллов базисные векторы измерений
являются векторами устремлений соответствующих трехмерных пространств. Используя
эти векторы, всегда имеется возможность войти вовнутрь того или иного свернутого
трехмерного собственного пространства.
Рассмотренные выше свойства универсального закона эволюции двойственного
отношения(монады) рассматривалось применительно к трехмерному собственному
пространству, совершенной формой которого являлся куб (звездный тетраэдр).
Теперь, в общем случае, зная, что все монадные кристаллы являются производными
от Платоновых тел, можно понять законы эволюции для высших измерений.
рис. 1
Эти
кристаллы можно назвать совершенными. При рассмотрении свойств монадных кристаллов мы уже рассматривали свойства
кристаллов формировать собственные пространства с числом измерений более трех. В
этих собственных пространствах монадных кристаллов базисные векторы измерений
являются векторами устремлений соответствующих трехмерных пространств. Используя
эти векторы, всегда имеется возможность войти вовнутрь того или иного свернутого
трехмерного собственного пространства.
Рассмотренные выше свойства универсального закона эволюции двойственного
отношения(монады) рассматривалось применительно к трехмерному собственному
пространству, совершенной формой которого являлся куб (звездный тетраэдр).
Теперь, в общем случае, зная, что все монадные кристаллы являются производными
от Платоновых тел, можно понять законы эволюции для высших измерений.
 êóá
èêîñàýäð
äîäåêàýäð
рис. 2
Совокупность вложенных друг в друга собственных пространств высших измерений
можно представить следующим образом (рис. 3).
êóá
èêîñàýäð
äîäåêàýäð
рис. 2
Совокупность вложенных друг в друга собственных пространств высших измерений
можно представить следующим образом (рис. 3).
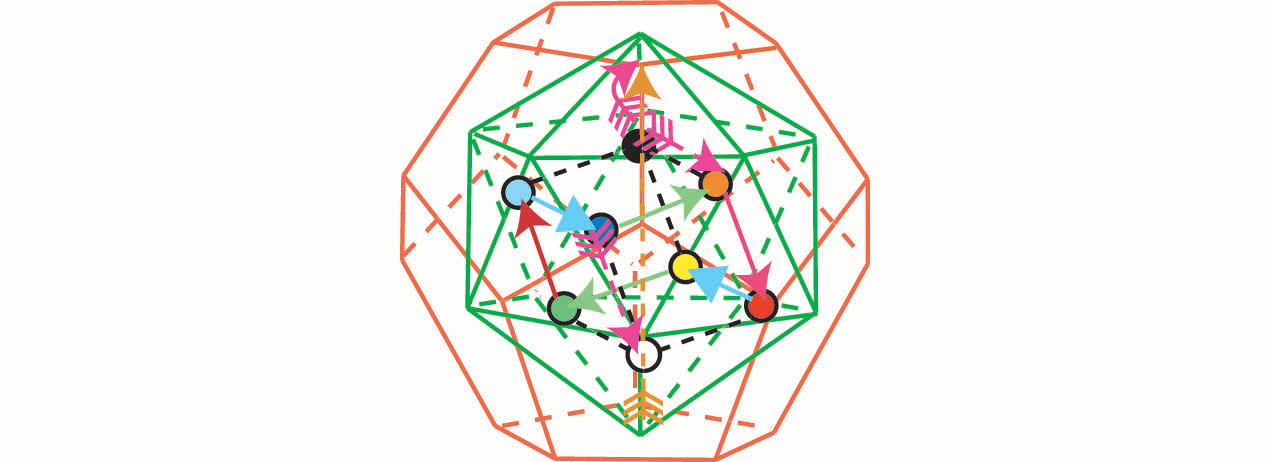 рис. 3-1
Анализ данных кристаллов выявляет некоторые
интересные особенности. Икосаэдр, с учетом ВЕЛИКОГО ПРЕДЕЛА (вершины в центре
кристалла) имеет 13 вершин. Додекаэдр, с учетом ВЕЛИКОГО ПРЕДЕЛА кристалла -21
вершину.
Если вспомним ряд Фибоначчи, то мы будем иметь
<1,1,2,3,5,8,13,21>
Íî îäíà èç ñàìûõ âååëèêèõ òàéí ìèðîçäàíèÿ
çàêëþ÷àåòñÿ â òîì, ÷òî ñâåðòêà âûñøèõ èçìåðåíèé â íèçøèå íåñåò â ñåáå çàêîíû
ñîõðàíåíèÿ ñèììåòðèè âûñøèõ èçìåðåíèé. Ïëàòîíîâû òåëà ìîãóò ïðîåêòèðîâàòüñÿ
íà ïëîñêîñòü, ñîõðàíÿÿ â ìàòðèöàõ íåîáõîäèìóþ èíôîðìàöèþ, ïî êîòîðîé ïëîñêóþ
ìàòðèöó ìîæíî ðàçâåðíóòü â âûñøèå ãèïåðïðîñòðàíñòâà.
рис. 3-1
Анализ данных кристаллов выявляет некоторые
интересные особенности. Икосаэдр, с учетом ВЕЛИКОГО ПРЕДЕЛА (вершины в центре
кристалла) имеет 13 вершин. Додекаэдр, с учетом ВЕЛИКОГО ПРЕДЕЛА кристалла -21
вершину.
Если вспомним ряд Фибоначчи, то мы будем иметь
<1,1,2,3,5,8,13,21>
Íî îäíà èç ñàìûõ âååëèêèõ òàéí ìèðîçäàíèÿ
çàêëþ÷àåòñÿ â òîì, ÷òî ñâåðòêà âûñøèõ èçìåðåíèé â íèçøèå íåñåò â ñåáå çàêîíû
ñîõðàíåíèÿ ñèììåòðèè âûñøèõ èçìåðåíèé. Ïëàòîíîâû òåëà ìîãóò ïðîåêòèðîâàòüñÿ
íà ïëîñêîñòü, ñîõðàíÿÿ â ìàòðèöàõ íåîáõîäèìóþ èíôîðìàöèþ, ïî êîòîðîé ïëîñêóþ
ìàòðèöó ìîæíî ðàçâåðíóòü â âûñøèå ãèïåðïðîñòðàíñòâà.
 êóá
èêîñàýäð
äîäåêàýäð
ðèñ 3-2
Âèäèòå, êàê ïîñëåäîâàòåëüíî, ñòóïåíüêà çà ñòóïåíüêîé. ôîðìèðóþòñÿ âèòêè
ñïèðàëè êðèñòàëëîâ, êàê ÷åòíûå âåðøèíû îòäåëÿþòñÿ îò íå÷åòíûõ, ôîðìèðóÿ
ìóæñêèå è æåíñêèå öåïî÷êè, ñïëåòàþùèåñÿ â åäèíóþ äâîéíóþ ñïèðàëü?
È ó âñåõ êðèñòàëëîâ ñóùåñòâóåò Âåëèêèé
ïðåäåë (òî÷êà ñáîðêè-ðàçáîðêè), â êîòîðóþ ìîæåò ñâîðà÷èâàòüñÿ êðèñòàëë è èç
êîòîðîé îí ìîæåò ðàçâîðà÷èâàòüñÿ.
Ýòà òî÷êà ñáîðêè-ðàçáîðêè ÿâëÿåòñÿ íóëü-ìåðíûì ãèïåðïðîñòðàíñòâîì (×èñëîì),
õðàíÿùèì â ñåáå âñå ñâîéñòâà ñîîòâåòñòâóþùåãî ãèïåðïðîñòðàíñòâà.
Ñ ó÷åòîì Âåëèêîãî ïðåäåëà ó Êóáà òàêèì ÷èñëîì ÿâëÿåòñÿ ÷èñëî 9, ó èêîñàýäðà
òàêèì ÷èñëîì áóäåò ÷èñëî 13, à ó äîäåêàýäðà òàêèì ÷èñëîì ÿâëÿåòñÿ 21. А теперь вспомним календарь древних майя (О
календаре майя).
êóá
èêîñàýäð
äîäåêàýäð
ðèñ 3-2
Âèäèòå, êàê ïîñëåäîâàòåëüíî, ñòóïåíüêà çà ñòóïåíüêîé. ôîðìèðóþòñÿ âèòêè
ñïèðàëè êðèñòàëëîâ, êàê ÷åòíûå âåðøèíû îòäåëÿþòñÿ îò íå÷åòíûõ, ôîðìèðóÿ
ìóæñêèå è æåíñêèå öåïî÷êè, ñïëåòàþùèåñÿ â åäèíóþ äâîéíóþ ñïèðàëü?
È ó âñåõ êðèñòàëëîâ ñóùåñòâóåò Âåëèêèé
ïðåäåë (òî÷êà ñáîðêè-ðàçáîðêè), â êîòîðóþ ìîæåò ñâîðà÷èâàòüñÿ êðèñòàëë è èç
êîòîðîé îí ìîæåò ðàçâîðà÷èâàòüñÿ.
Ýòà òî÷êà ñáîðêè-ðàçáîðêè ÿâëÿåòñÿ íóëü-ìåðíûì ãèïåðïðîñòðàíñòâîì (×èñëîì),
õðàíÿùèì â ñåáå âñå ñâîéñòâà ñîîòâåòñòâóþùåãî ãèïåðïðîñòðàíñòâà.
Ñ ó÷åòîì Âåëèêîãî ïðåäåëà ó Êóáà òàêèì ÷èñëîì ÿâëÿåòñÿ ÷èñëî 9, ó èêîñàýäðà
òàêèì ÷èñëîì áóäåò ÷èñëî 13, à ó äîäåêàýäðà òàêèì ÷èñëîì ÿâëÿåòñÿ 21. А теперь вспомним календарь древних майя (О
календаре майя).
 рис. 4
В этом календаре 3
"шестеренки" с числом зубьев 8, 13, 20.
Этот рисунок несет в себе тайны рождения Пирамиды Силы (Пирамида
Силы) и тайны рождения хроматических гамм собственных пространств (Гаммы
Сил).
Если учесть, что "Последний может
замыкаться на Первый", то мы получим замкнутый мир кристаллов.
Этот мир чрезвычайно богат и многообразен, но он порождается всего ПЯТЬЮ
СИЛАМИ (черные клавиши) хроматической гаммы нашего мироздания.
Посмотрите и увидьте, что эти пять сил присутствуют и в календаре древних
майя. Видите в центре белую и черную двойную спираль?
Видите. что каждая из них сопряжена с собственным крестом?
А теперь вспомните библейское "Да
будет свет!". И белая
пирамида становится ПЯТЬЮ СИЛАМИ, порождающими все многообразие кристаллов
нашего мироздания.
Отметим некоторые важные свойства многомерных собственных
пространств.
1. Все собственные подпространства любого собственного многомерного пространства
содержатся в этом многомерном пространстве.
2.
Собственные пространства (подпространства) высших измерений, в соответствии с
закономерностью о замкнутости, могут формировать замкнутые циклы обхода вершин
соответствующих базисных векторов устремлений этих пространств. При этом
роль подпространств в этих пространствах могут играть трехмерные пространства (триангуляры),
или пространства с большим числом измерений.
3. Собственные пространства, в силу закономерности о преемственности, могут
трансформироваться в собственные пространства других измерений, с меньшим
или большим числом измерений, Свойство преемственности пространств
позволяет осуществлять свертки и развертки пространств.
4. Число измерений
собственных пространств является ограниченным. Каждый раз,
когда число измерений собственного пространства превышает установленный
предел, происходит перенормировка
числа измерений. И Последний становится Первым.
Кристалл перерождается в сферу. Мужское становится
женским и эволюция начинается сначала.
Однако инвариантность
преобразований позволяет, при необходимости, всегда осуществить развертку
соответствующих собственных пространств, как бы сложны они ни были. Это свойство
является одним из самых замечательных свойств, порождаемых Универсальным законом
эволюции. Это свойство периодичности изменения
сложности собственных пространств может лежать в основе памяти
биологических клеток живых организмов (и человека) о всей совокупности
своих прежних "жизней". Эта периодичность может лежать в основе формирования
тонких тел из соответствующей совокупности биоклеток.
При этом может случиться и так, что только сама клетка может "вспомнить" свои
прошлые "жизни", восстановить память веков. Попытка насильно развернуть ее
собственные пространства, не имея соответствующего изначального "ключа", может
классифицироваться как попытка "взлома"и последующим за этим
самоуничтожением, сопровождающимся выделением соответствующих психических
(тонких) энергий.
Каждый уровень
иерархии собственных пространств монадных кристаллов, может характеризоваться
определенными правилами порождения собственных измерений.
2. СВОЙСТВА МНОГОМЕРНЫХ МОНАД
2.1.
Внешняя и внутренняя двойственность.
Монада, с точки
зрения Единого закона, является многоуровневым объектом. Но у любой монады, к
какому бы она уровню иерархии не принадлежала, существует два основных качества.
Любая монада, с точки зрения двойственности е структуры, может рассматриваться
как объект с внешней или внутренней двойственностью. Монаду
можно рассматривать как узловую точку между двумя собственными
пространствами. Поэтому, с точки зрения собственного пространства более низкого
уровня монада может иметь внутреннюю структуру. С позиций собственного
пространства, формируемого данной монадой, она может рассматриваться
как одномерный объект ( с внутренней двойственностью), или как двумерный объект
(с внешней двойственностью).
2.2.
Периодичность свойств
Свойства монады при последовательном обходе по кресту испытывают периодическую
трансформацию.
рис. 4
В этом календаре 3
"шестеренки" с числом зубьев 8, 13, 20.
Этот рисунок несет в себе тайны рождения Пирамиды Силы (Пирамида
Силы) и тайны рождения хроматических гамм собственных пространств (Гаммы
Сил).
Если учесть, что "Последний может
замыкаться на Первый", то мы получим замкнутый мир кристаллов.
Этот мир чрезвычайно богат и многообразен, но он порождается всего ПЯТЬЮ
СИЛАМИ (черные клавиши) хроматической гаммы нашего мироздания.
Посмотрите и увидьте, что эти пять сил присутствуют и в календаре древних
майя. Видите в центре белую и черную двойную спираль?
Видите. что каждая из них сопряжена с собственным крестом?
А теперь вспомните библейское "Да
будет свет!". И белая
пирамида становится ПЯТЬЮ СИЛАМИ, порождающими все многообразие кристаллов
нашего мироздания.
Отметим некоторые важные свойства многомерных собственных
пространств.
1. Все собственные подпространства любого собственного многомерного пространства
содержатся в этом многомерном пространстве.
2.
Собственные пространства (подпространства) высших измерений, в соответствии с
закономерностью о замкнутости, могут формировать замкнутые циклы обхода вершин
соответствующих базисных векторов устремлений этих пространств. При этом
роль подпространств в этих пространствах могут играть трехмерные пространства (триангуляры),
или пространства с большим числом измерений.
3. Собственные пространства, в силу закономерности о преемственности, могут
трансформироваться в собственные пространства других измерений, с меньшим
или большим числом измерений, Свойство преемственности пространств
позволяет осуществлять свертки и развертки пространств.
4. Число измерений
собственных пространств является ограниченным. Каждый раз,
когда число измерений собственного пространства превышает установленный
предел, происходит перенормировка
числа измерений. И Последний становится Первым.
Кристалл перерождается в сферу. Мужское становится
женским и эволюция начинается сначала.
Однако инвариантность
преобразований позволяет, при необходимости, всегда осуществить развертку
соответствующих собственных пространств, как бы сложны они ни были. Это свойство
является одним из самых замечательных свойств, порождаемых Универсальным законом
эволюции. Это свойство периодичности изменения
сложности собственных пространств может лежать в основе памяти
биологических клеток живых организмов (и человека) о всей совокупности
своих прежних "жизней". Эта периодичность может лежать в основе формирования
тонких тел из соответствующей совокупности биоклеток.
При этом может случиться и так, что только сама клетка может "вспомнить" свои
прошлые "жизни", восстановить память веков. Попытка насильно развернуть ее
собственные пространства, не имея соответствующего изначального "ключа", может
классифицироваться как попытка "взлома"и последующим за этим
самоуничтожением, сопровождающимся выделением соответствующих психических
(тонких) энергий.
Каждый уровень
иерархии собственных пространств монадных кристаллов, может характеризоваться
определенными правилами порождения собственных измерений.
2. СВОЙСТВА МНОГОМЕРНЫХ МОНАД
2.1.
Внешняя и внутренняя двойственность.
Монада, с точки
зрения Единого закона, является многоуровневым объектом. Но у любой монады, к
какому бы она уровню иерархии не принадлежала, существует два основных качества.
Любая монада, с точки зрения двойственности е структуры, может рассматриваться
как объект с внешней или внутренней двойственностью. Монаду
можно рассматривать как узловую точку между двумя собственными
пространствами. Поэтому, с точки зрения собственного пространства более низкого
уровня монада может иметь внутреннюю структуру. С позиций собственного
пространства, формируемого данной монадой, она может рассматриваться
как одномерный объект ( с внутренней двойственностью), или как двумерный объект
(с внешней двойственностью).
2.2.
Периодичность свойств
Свойства монады при последовательном обходе по кресту испытывают периодическую
трансформацию.

Данный рисунок показывает, что в результате зеркального самокопирования
монады, послеждняя претерпевает периодические качественные изменения.
Если при самокопировании монады из квадрата
I квадрат II
структура монады не изменяется, то при самокопировании в квадрат III
структура претерпевает качественные измерения. "Внешнее
становится внутренним". Монада
с внешней двойственностью трансформируется в
монаду с внутренней двойственностью. Затем происходит ее самокопирование в
квадрат IV.
А вот процесс самокопирования из квадрата IV в квадрат
I снова приводит к качественным изменениям. "Внутреннее
становится внешним." Монада с внутренней
двойственностью трансформируется в монаду с внешней двойственностью. Она
становится дуадой. Далее процесс повторяется.
Поэтому
периодичность свойств монады не может не отражаться на периодичности изменения
свойств любого материального объекта. Периодичность эволюции любой
иерархической системы обусловлена периодичностью изменения свойств монады.
При этом свойства лепестков
монады
(<+1,-i>,
<-i,+1>)
и
(<+1,-i>,
<-i,+1>)
изменяются
в соответствии со свойствами "Розы Мёбиуса".
Приведенная ниже
таблица 1 отражает многомерные свойства монады.
Таблица 1.
| № п/п |
Состав |
Монада |
Состав |
Монадный
крест |
| 1 |
1,1 |
монада
|
2,2 |
звездная
монада |
| 2 |
2,2 |
монадная
дуада |
4,4 |
звездная
квадра (тетраэдр) |
| 3 |
3,3 |
монадная
триада |
6,6 |
звездная
гексада |
| 4 |
4,4 |
монадная
квадра |
8,8 |
звездная
квадра |
| 5 |
5,5 |
монадная
пентада |
10,10 |
звездная
пентада |
| 6 |
6,6 |
монадная
гексада |
12,12 |
звездная
гексада |
| 7 |
7,7 |
монадная
гептада |
14,14 |
звездная
гептада |
| 8 |
8,8 |
монадная
окдоада |
16,16 |
звездная
огдоада |
| 9 |
9,9 |
монадная
эннеада |
18,18 |
звездная
эннеада |
С каждым из приведенных в таблице монадных объектов связано множество древних
легенд.
Приведем краткую информацию о некоторых из
приведенных в таблице монадных формах.
Монада
(1).
Число с одним параметром
символизирует целостность. Это первоå движение Бездны и возникновение
Универсального ума (или Бога). Это монолит, вмещающий в себя все, кроме начала и
конца. Но монада обладает внутренней двойственностью.
Дуада (2).
Разделение монады на два полярных понятие. Это монада - с внешней
двойственностью.
Триада
(3).
Полное равновесие Дуады и Монады. Это
вторичное образование Целостности в форме триединства.
Тетрада
(4).
Последняя главная образующая величина, непосредственно формирующая видимый мир из
четырех первоэлементов. Это ключ к Земле и Небу, открывающий духовное и
материальное совершенство.
Пентада
(5).
Все характеристики монадных форм, идущих после тетрады, есть зеркальное
отражение монадных форм, стоящих до них. Пентада предстает как
пятиконечная звезда. "Пентаграмма, - пишет Э.Леви в книге "Ритуал трансцеíдентной
магии",- это фигура, изображающая человеческое тело, имеющего четыре члена и
одну точку, представляющую собой голову".
Гексада
(6).
Это единство двух триад, олицетворение гармонии между микро- и макрокосмом,
между мужским и женским началом. Это дуада, каждый полюс которой является
триединым (триадой).
Гептада
(7).
Это зеркальное отражение
äуады. Её можно
представить как бипирамиду с пентадным основанием.
Огдоада
(8). Символическое начертание Огдоада -
это две переплетающиеся змеи на дрåвних символах, олицетворяющих
совершенство и бесконечность. Это "перекладина" креста из звездных тетраэдров.
Эннеада
(9).
Это Великий Предел, Абсолютная
Целостность. Это точка, в которой внешнее становится внутренним, а
внутреннее становится внешним. На входе в эту точку мужское становится
женским. Но на выходе, наоборот, женское становится мужским.
2.3.
Монадное триединство
Монада в таблице может рассматриваться и как объект с внутренней
двойственностью, а крест - как совокупность двух перекладин монадного
креста, одна из которых является монадой с внутренней двойственностью, а другая
- с внешней двойственностью.
В этом случае
такая форма монадного креста будет характеризовать структуру триады -триединство
монад, "кварковый" состав монадного креста, порождающего те или иные
монадные семейства. Из таблицы видно, что такие свойства монады могут иметь
на любом уровне иерархии, т.е. "монадные кварки" также являются
многоуровневыми.
Íà ñòðàíèöå "Î
òðèåäèíñòâå" ìû ïîêàçàëè, ÷òî ýâîëþöèÿ Âåëèêîãî ïðåäåëà ÒÀÉ ÖÇÈ
ïîðîæäàåò, ïî îáðàçó è ïîäîáèþ òðèàäó.
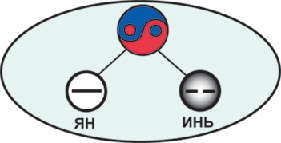 êîòîðàÿ
ïîðîæäàåò 8 òðèãðàìì (òðèàä) È-Öçèí (Êíèãà ïåðåìåí).
êîòîðàÿ
ïîðîæäàåò 8 òðèãðàìì (òðèàä) È-Öçèí (Êíèãà ïåðåìåí).
 ðèñ.
5
Äàííûé ðèñóíîê îòðàæàåò çàìå÷àòåëüíûå ñâîéñòâà ìîíàäû "ÿí-èíü". Îí
ïîêàçûâàåò, êàêèì îáðàçîì, ïî îáðàçó è ïîäîáèþ, èç òðèåäèíîãî Çàìûñëà ìîíàäû
ôîðìèðóåòñÿ Êóá òðèãðàììà È-Öçèí.
3.
СВОЙСТВА ВЫСШИХ ИЗМЕРЕНИЙ
Ãîâîðÿ î âûñøèõ
èçìåðåíèÿõ ñîáñòâåííûõ ïðîñòðàíñòâ, ñëåäóåò ñêàçàòü è î òîì, ÷òî ñîâåðøåííàÿ
ôîðìà êóáà, õàðàêòåðèçóþùàÿ ñâîéñòâà èçìåðåíèé íàøåãî ìèðîçäàíèÿ, íå
ÿâëÿåòñÿ åäèíñòâåííîé, î ÷åì ñâèäåòåëüñòâóþò Ïëàòîíîâû òåëà (ðèñ. 1).
ðèñ.
5
Äàííûé ðèñóíîê îòðàæàåò çàìå÷àòåëüíûå ñâîéñòâà ìîíàäû "ÿí-èíü". Îí
ïîêàçûâàåò, êàêèì îáðàçîì, ïî îáðàçó è ïîäîáèþ, èç òðèåäèíîãî Çàìûñëà ìîíàäû
ôîðìèðóåòñÿ Êóá òðèãðàììà È-Öçèí.
3.
СВОЙСТВА ВЫСШИХ ИЗМЕРЕНИЙ
Ãîâîðÿ î âûñøèõ
èçìåðåíèÿõ ñîáñòâåííûõ ïðîñòðàíñòâ, ñëåäóåò ñêàçàòü è î òîì, ÷òî ñîâåðøåííàÿ
ôîðìà êóáà, õàðàêòåðèçóþùàÿ ñâîéñòâà èçìåðåíèé íàøåãî ìèðîçäàíèÿ, íå
ÿâëÿåòñÿ åäèíñòâåííîé, î ÷åì ñâèäåòåëüñòâóþò Ïëàòîíîâû òåëà (ðèñ. 1).
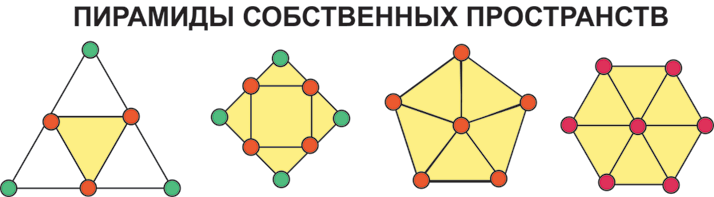 ðèñ. 6-1
ðèñ. 6-2
ðèñ. 6-3
ðèñ. 6-4
Íà äàííîì ðèñóíêå ïðèâåäåíû ïèðàìèäû
èçìåðåíèé äëÿ ñîáñòâåííûõ ïðîñòðàíñòâ Çàìûñåë ýâîëþöèè ìîíàäû êîòîðûõ
ñîäåðæèò ñîîòâåòñòâåííî 3, 4, 5 è 6 èçìåðåíèé.
Ýòè ïðîåêöèè
ìíîãîìåðíûõ ïðîñòðàíñòâ íà ïëîñêîñòè ìîæíî èíòåðïðåòèðîâàòü è êàê ïèðàìèäû ñ
ñîîòâåòñòâóþùèì îñíîâàíèåì. Òîãäà ìû ïîëó÷èì ïî ñóòè ðàçâåðòêè òðåóãîëüíîé
(ðèñ. 6-1) è ÷åòûðåõóãîëüíîé ïèðàìèäû (ðèñ. 6-2), ïÿòèóãîëüíóþ è
øåñòèóãîëüíóþ ïèðàìèäó.
Íà ñòðàíèöàõ "Êîíöåïöèè"
è "Ñòðóêòóðû" áûëè îáîñíîâàíû ñâîéñòâà
êîíöåïòóàëüíûõ è ñòðóêòóðíûõ ìíîãî÷ëåíîâ. Áûëî ïîêàçàíî, êàê èç Çàìûñëà
Òâîðåíèÿ
W0
ôîðìèðóþòñÿ
ñîîòâåòñòâóþùèå ñòðóêòóðíûå èçìåðåíèÿ
ðèñ. 6-1
ðèñ. 6-2
ðèñ. 6-3
ðèñ. 6-4
Íà äàííîì ðèñóíêå ïðèâåäåíû ïèðàìèäû
èçìåðåíèé äëÿ ñîáñòâåííûõ ïðîñòðàíñòâ Çàìûñåë ýâîëþöèè ìîíàäû êîòîðûõ
ñîäåðæèò ñîîòâåòñòâåííî 3, 4, 5 è 6 èçìåðåíèé.
Ýòè ïðîåêöèè
ìíîãîìåðíûõ ïðîñòðàíñòâ íà ïëîñêîñòè ìîæíî èíòåðïðåòèðîâàòü è êàê ïèðàìèäû ñ
ñîîòâåòñòâóþùèì îñíîâàíèåì. Òîãäà ìû ïîëó÷èì ïî ñóòè ðàçâåðòêè òðåóãîëüíîé
(ðèñ. 6-1) è ÷åòûðåõóãîëüíîé ïèðàìèäû (ðèñ. 6-2), ïÿòèóãîëüíóþ è
øåñòèóãîëüíóþ ïèðàìèäó.
Íà ñòðàíèöàõ "Êîíöåïöèè"
è "Ñòðóêòóðû" áûëè îáîñíîâàíû ñâîéñòâà
êîíöåïòóàëüíûõ è ñòðóêòóðíûõ ìíîãî÷ëåíîâ. Áûëî ïîêàçàíî, êàê èç Çàìûñëà
Òâîðåíèÿ
W0
ôîðìèðóþòñÿ
ñîîòâåòñòâóþùèå ñòðóêòóðíûå èçìåðåíèÿ
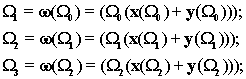 Çäåñü êàæäûé ïîñëåäóþùèé ìíîãî÷ëåí ôîðìèðóåòñÿ, ïî îáðàçó
è ïîäîáèþ èç ïðåäûäóùåãî, èñïîëüçóÿ ðåêóðñèâíûé ìåõàíèçì ïîðîæäåíèÿ äàííîãî
êëàññà ñòðóêòóð. Çäåñü Çàìûñåë èãðàåò ðîëü íåïðèâîäèìîãî áàçèñíîãî ýëåìåíòà
ñòðóêòóðû.
Çäåñü êàæäûé ïîñëåäóþùèé ìíîãî÷ëåí ôîðìèðóåòñÿ, ïî îáðàçó
è ïîäîáèþ èç ïðåäûäóùåãî, èñïîëüçóÿ ðåêóðñèâíûé ìåõàíèçì ïîðîæäåíèÿ äàííîãî
êëàññà ñòðóêòóð. Çäåñü Çàìûñåë èãðàåò ðîëü íåïðèâîäèìîãî áàçèñíîãî ýëåìåíòà
ñòðóêòóðû.
 ðèñ.6-5
ðèñ.6-5
 ðèñ
6-6
Íà äàííûõ
ðèñóíêàõ ïîêàçàíî, êàê ïî îáðàçó è ïîäîáèþ Çàìûñëà Òâîðåíèÿ (â öåíòðå
ñîîòâåòñòâóþùèõ ðèñóíêîâ) ñîîòâåòñòâóþùèõ ñîáñòâåííûõ ïðîñòðàíñòâ
ôîðìèðóþòñÿ âñå åãî îáîëî÷êè è ïîäîáîëî÷êè.
 âåðõíåé ÷àñòè ðèñóíêà 6-6 ñëåâà ïîêàçàíà ïîëîâèííàÿ
ðàçâåðòêà äîäåêàýäðà.  âåðõíåé ÷àñòè ðèñóíêà ñïðàâà ïîêàçàíà ÷àñòü
ðàçâåðòêè èêîñàýäðà. Èç ýòèõ ðàçâåðòîê âèäíî, êàê ïî îáðàçó è ïîäîáèþ
Çàìûñëà ñîîòâåòñòâóþùèõ ïðîñòðàíñòâ ïðîèñõîäèò èõ ìàòåðèàëèçàöèÿ, ò.å. íà
êàæäîì ýòàïå ôîðìèðóåòñÿ ñòðóêòóðà, èíâàðèàíòíàÿ Çàìûñëó Òâîðåíèÿ
ñîáñòâåííîãî ïðîñòðàíñòâà.
Èç
ïðèâåäåííûõ âûøå ðèñóíêîâ íåïîñðåäñòâåííî âèäíî, ÷òî
òðèàäà ïîèñòèíå ÿâëÿåòñÿ
ñèñòåìîîáðàçóþùåé òðèàäîé Ìèðîçäàíèÿ ëþáîãî óðîâíÿ èåðàðõèè. Ýòîò ðèñóíîê ïîëíîñòüþ àíàëîãè÷åí ðèñóíêó èç Êíèãè
Ïåðåìåí
ðèñ
6-6
Íà äàííûõ
ðèñóíêàõ ïîêàçàíî, êàê ïî îáðàçó è ïîäîáèþ Çàìûñëà Òâîðåíèÿ (â öåíòðå
ñîîòâåòñòâóþùèõ ðèñóíêîâ) ñîîòâåòñòâóþùèõ ñîáñòâåííûõ ïðîñòðàíñòâ
ôîðìèðóþòñÿ âñå åãî îáîëî÷êè è ïîäîáîëî÷êè.
 âåðõíåé ÷àñòè ðèñóíêà 6-6 ñëåâà ïîêàçàíà ïîëîâèííàÿ
ðàçâåðòêà äîäåêàýäðà.  âåðõíåé ÷àñòè ðèñóíêà ñïðàâà ïîêàçàíà ÷àñòü
ðàçâåðòêè èêîñàýäðà. Èç ýòèõ ðàçâåðòîê âèäíî, êàê ïî îáðàçó è ïîäîáèþ
Çàìûñëà ñîîòâåòñòâóþùèõ ïðîñòðàíñòâ ïðîèñõîäèò èõ ìàòåðèàëèçàöèÿ, ò.å. íà
êàæäîì ýòàïå ôîðìèðóåòñÿ ñòðóêòóðà, èíâàðèàíòíàÿ Çàìûñëó Òâîðåíèÿ
ñîáñòâåííîãî ïðîñòðàíñòâà.
Èç
ïðèâåäåííûõ âûøå ðèñóíêîâ íåïîñðåäñòâåííî âèäíî, ÷òî
òðèàäà ïîèñòèíå ÿâëÿåòñÿ
ñèñòåìîîáðàçóþùåé òðèàäîé Ìèðîçäàíèÿ ëþáîãî óðîâíÿ èåðàðõèè. Ýòîò ðèñóíîê ïîëíîñòüþ àíàëîãè÷åí ðèñóíêó èç Êíèãè
Ïåðåìåí
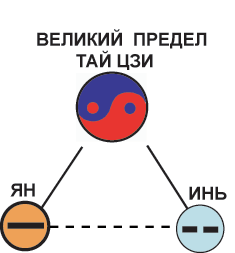 ðèñ. 7-1
Ýòà òðèàäà ñïîñîáíà ôîðìèðîâàòü ñîáñòâåííîå
òðèàäíîå ãèïåðïðîñòðàíñòâî. Ýòî "ïëîñêîå" ãèïåðïðîñòðàíñòâî. Îíî
ïðåäñòàâëÿåò ñîáîé ñèñòåìó âëîæåííûõ äðóã â äðóãà òðåóãîëüíèêîâ (òðèàä,
òðèãðàìì). Ïðèìåðîì òàêîãî ãèïåðïðîñòðàíñòâà, ìîæåò ñëóæèòü ôèãóðà,
ñîñòàâëåííàÿ èç äåñÿòè òî÷åê -óçëîâ, èçâåñòíàÿ åùå ïèôàãîðåéöàì, ñ êîòîðîé
îíè
îëèöåòâîðÿëè ïîëíîòó âñåìèðíîé ïóñòîòû è
Æèâîòâîðÿùèé êðåñò.
ðèñ. 7-1
Ýòà òðèàäà ñïîñîáíà ôîðìèðîâàòü ñîáñòâåííîå
òðèàäíîå ãèïåðïðîñòðàíñòâî. Ýòî "ïëîñêîå" ãèïåðïðîñòðàíñòâî. Îíî
ïðåäñòàâëÿåò ñîáîé ñèñòåìó âëîæåííûõ äðóã â äðóãà òðåóãîëüíèêîâ (òðèàä,
òðèãðàìì). Ïðèìåðîì òàêîãî ãèïåðïðîñòðàíñòâà, ìîæåò ñëóæèòü ôèãóðà,
ñîñòàâëåííàÿ èç äåñÿòè òî÷åê -óçëîâ, èçâåñòíàÿ åùå ïèôàãîðåéöàì, ñ êîòîðîé
îíè
îëèöåòâîðÿëè ïîëíîòó âñåìèðíîé ïóñòîòû è
Æèâîòâîðÿùèé êðåñò.
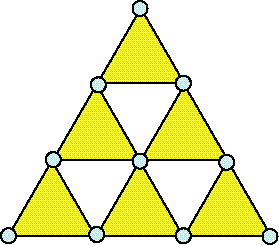 ðèñ. 7-2
Èç ýòèõ 9 òðèãðàìì ñòðîÿòñÿ óæå ïðîñòðàíñòâåííûå Ïëàòîíîâû òåëà.
Ìíîãèå ó÷åíûå óæå ïîçíàëè çàêîíû ñèììåòðèè
è âçàèìíîñòè âçàèìîñâÿçè Ïëàòîíîâûõ òåë äðóã ñ äðóãîì.
Ïîçíàëè è... ïîòåðÿëè âñÿêèé èíòåðåñ ê
äàëüíåéøåìó èçó÷åíèþ ñâîéñòâ Ïëàòîíîâûõ òåë. È íàïðàñíî.
Ýòè òåëà åùå íå ðàñêðûëè ëþäÿì ñâîè ñàìûå
ñîêðîâåííûå òàéíû.
Ðàññìîòðèì âíà÷àëå ïðååìñòâåííîñòü ôîðìèðîâàíèÿ òåòðàýäðîâ, îêòàýäðîâ è
êóáà.
ðèñ. 7-2
Èç ýòèõ 9 òðèãðàìì ñòðîÿòñÿ óæå ïðîñòðàíñòâåííûå Ïëàòîíîâû òåëà.
Ìíîãèå ó÷åíûå óæå ïîçíàëè çàêîíû ñèììåòðèè
è âçàèìíîñòè âçàèìîñâÿçè Ïëàòîíîâûõ òåë äðóã ñ äðóãîì.
Ïîçíàëè è... ïîòåðÿëè âñÿêèé èíòåðåñ ê
äàëüíåéøåìó èçó÷åíèþ ñâîéñòâ Ïëàòîíîâûõ òåë. È íàïðàñíî.
Ýòè òåëà åùå íå ðàñêðûëè ëþäÿì ñâîè ñàìûå
ñîêðîâåííûå òàéíû.
Ðàññìîòðèì âíà÷àëå ïðååìñòâåííîñòü ôîðìèðîâàíèÿ òåòðàýäðîâ, îêòàýäðîâ è
êóáà.
 ðèñ. 7-3
Èçâåñòíî, ÷òî êóá è îêòàýäð ÿâëÿþòñÿ âçàèìíûìè. Åñëè ó îäíîãî èç ýòèõ
ìíîãîãðàííèêîâ ñîåäèíèòü îòðåçêàìè ïðÿìûõ öåíòðû ãðàíåé, èìåþùèõ îáùåå
ðåáðî, òî ïîëó÷èòñÿ äðóãîé ìíîãîãðàííèê.
Ýòó âçàèìíîñòü ìîæíî îòðàçèòü â âèäå ìîíàäíûõ âåñîâ
ðèñ. 7-3
Èçâåñòíî, ÷òî êóá è îêòàýäð ÿâëÿþòñÿ âçàèìíûìè. Åñëè ó îäíîãî èç ýòèõ
ìíîãîãðàííèêîâ ñîåäèíèòü îòðåçêàìè ïðÿìûõ öåíòðû ãðàíåé, èìåþùèõ îáùåå
ðåáðî, òî ïîëó÷èòñÿ äðóãîé ìíîãîãðàííèê.
Ýòó âçàèìíîñòü ìîæíî îòðàçèòü â âèäå ìîíàäíûõ âåñîâ
 ò.å. ýòè êðèñòàëëû ÿâëÿþòñÿ êàê áû
âûâåðíóòûìè äðóã îòíîñèòåëüíî äðóãà íàèçíàíêó. Åñëè îêòàýäð áóäåò îòðàæàòü
ÿíñêèé àñïåêò, òî êóá áóäåò îòðàæàòü óæå èíüñêèé àñïåêò. Êðîìå òîãî, ó ýòèõ
ìíîãîãðàííèêîâ ÷èñëî âåðøèí è ÷èñëî ãðàíåé îêàçûâàþòñÿ òàêæå âçàèìíû. Â
îêòàýäðå ÷èñëî âåðøèí ðàâíî 6, à ÷èñëî ãðàíåé ðàâíî 8.  êóáå íàîáîðîò,
÷èñëî âåðøèí ðàâíî 8, à ÷èñëî ãðàíåé ðàâíî 6.
ò.å. ýòè êðèñòàëëû ÿâëÿþòñÿ êàê áû
âûâåðíóòûìè äðóã îòíîñèòåëüíî äðóãà íàèçíàíêó. Åñëè îêòàýäð áóäåò îòðàæàòü
ÿíñêèé àñïåêò, òî êóá áóäåò îòðàæàòü óæå èíüñêèé àñïåêò. Êðîìå òîãî, ó ýòèõ
ìíîãîãðàííèêîâ ÷èñëî âåðøèí è ÷èñëî ãðàíåé îêàçûâàþòñÿ òàêæå âçàèìíû. Â
îêòàýäðå ÷èñëî âåðøèí ðàâíî 6, à ÷èñëî ãðàíåé ðàâíî 8.  êóáå íàîáîðîò,
÷èñëî âåðøèí ðàâíî 8, à ÷èñëî ãðàíåé ðàâíî 6.
 ðèñ. 7-4
Àíàëîãè÷íûìè ñâîéñòâàìè îáëàäàþò èêîñàýäð è
äîäåêàýäð. Îíè òîæå ïî îòíîøåíèþ äðóã ê äðóãó ÿâëÿþòñÿ êàê áû âûâåðíóòûìè
íàèçíàíêó, íåñÿ â ñåáå ÿíñêèé è èíüñêèé àñïåêòû.
ðèñ. 7-4
Àíàëîãè÷íûìè ñâîéñòâàìè îáëàäàþò èêîñàýäð è
äîäåêàýäð. Îíè òîæå ïî îòíîøåíèþ äðóã ê äðóãó ÿâëÿþòñÿ êàê áû âûâåðíóòûìè
íàèçíàíêó, íåñÿ â ñåáå ÿíñêèé è èíüñêèé àñïåêòû.
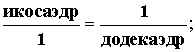 Ó èêîñàýäðà 12 âåðøèí è 20 ãðàíåé, ó
äîäåêàýäðà íàîáîðîò, 20 âåðøèí è 12 ãðàíåé.
Íî êàêèì îáðàçîì èç êóáà
ôîðìèðóåòñÿ èêîñàýäð, à èç òåòðàýäðà ôîðìèðóåòñÿ îêòàýäð?
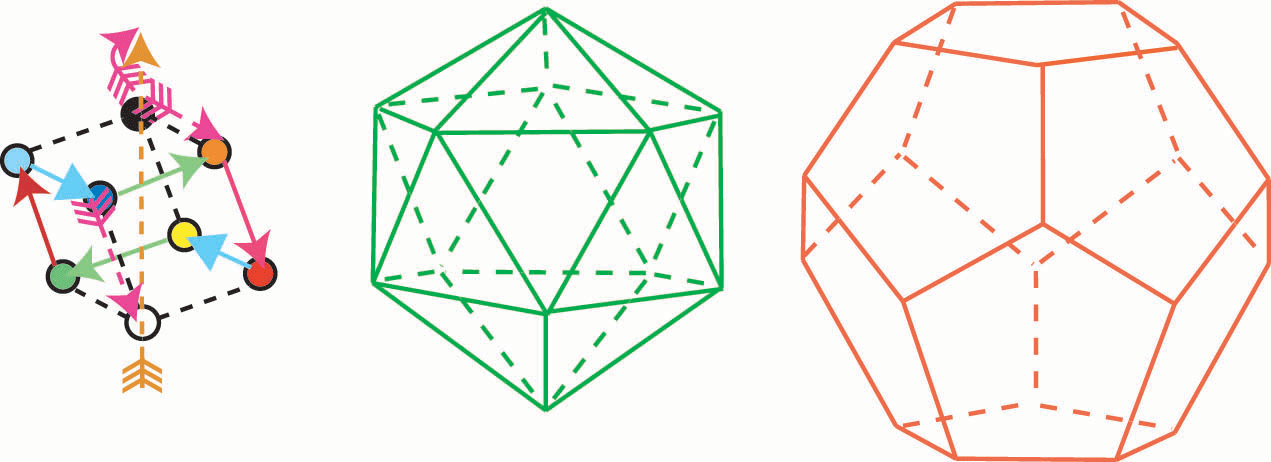
Íà ýòîò âîïðîñ îòâåò áóäåò äàí íèæå, ïðè àíàëèçå ñâîéñòâ
ìàòðèöû ãèïåðèêîñàýäðà è ãèïåðäîäåêàýäðà.
3.1.
ПЯТИМЕРНОЕ ПРОСТРАНСТВО
Рассмотрим
â êà÷åñòâå ïðèìåðà íåêîòîðûå
свойства пятимерного собственного пространства. Так,
из рисунков 2 и 3
видно, что в собственных пространствах высших измерений (более трех) в качестве
"ячеек" монадной оболочки используются уже пятиугольники, в то время как в
трехмерном кристалле (кубе) проекция на некоторую плоскость является
шестиугольником. Следовательно и правила обхода вершин, являющихся концами
векторов устремлений соответствующих собственных подпространств, должны
отличаться от правил обхода вершин в трехмерных собственных пространствах
(кубе). Возможно, что в пятиугольнике, как проекции соответствующего монадного
кристалла на плоскость, эти правила могут определяться лучами пятиугольной
звезды (рис. 7-1).
Ó èêîñàýäðà 12 âåðøèí è 20 ãðàíåé, ó
äîäåêàýäðà íàîáîðîò, 20 âåðøèí è 12 ãðàíåé.
Íî êàêèì îáðàçîì èç êóáà
ôîðìèðóåòñÿ èêîñàýäð, à èç òåòðàýäðà ôîðìèðóåòñÿ îêòàýäð?
Íà ýòîò âîïðîñ îòâåò áóäåò äàí íèæå, ïðè àíàëèçå ñâîéñòâ
ìàòðèöû ãèïåðèêîñàýäðà è ãèïåðäîäåêàýäðà.
3.1.
ПЯТИМЕРНОЕ ПРОСТРАНСТВО
Рассмотрим
â êà÷åñòâå ïðèìåðà íåêîòîðûå
свойства пятимерного собственного пространства. Так,
из рисунков 2 и 3
видно, что в собственных пространствах высших измерений (более трех) в качестве
"ячеек" монадной оболочки используются уже пятиугольники, в то время как в
трехмерном кристалле (кубе) проекция на некоторую плоскость является
шестиугольником. Следовательно и правила обхода вершин, являющихся концами
векторов устремлений соответствующих собственных подпространств, должны
отличаться от правил обхода вершин в трехмерных собственных пространствах
(кубе). Возможно, что в пятиугольнике, как проекции соответствующего монадного
кристалла на плоскость, эти правила могут определяться лучами пятиугольной
звезды (рис. 7-1).

ðèñ. 7-5
Из рисунка видно, что последовательность порождения вершин этого монадного
кристалла также не является случайной, как и в случае трехмерных монадных
êðèñòàëëîâ. Ýòîìó ïëîñêîìó ðèñóíêó ìîæåò ñîîòâåòñòâîâàòü óæå ÷åòûðåõãðàííàÿ
ïèðàìèäà (ðèñ. 7-6).
 ðèñ.
7-6
На данном рисунке
приведена последовательность обхода кристалла в процессе его формирования. Из
рисунка видно, что начав обход из вершины пирамиды, мы далее совершаем прежний
"обход по кресту". Но как только обход по кресту оказывается завершенным, и
возникает замкнутая "силовая линия", структура кристалла подвергается
"перестройке" (рис.
8).
ðèñ.
7-6
На данном рисунке
приведена последовательность обхода кристалла в процессе его формирования. Из
рисунка видно, что начав обход из вершины пирамиды, мы далее совершаем прежний
"обход по кресту". Но как только обход по кресту оказывается завершенным, и
возникает замкнутая "силовая линия", структура кристалла подвергается
"перестройке" (рис.
8).
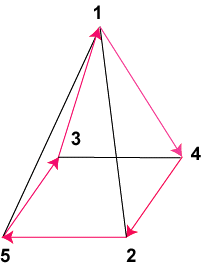
рис. 8
Но такой кристалл может образовать и
трехгранная бипирамида.
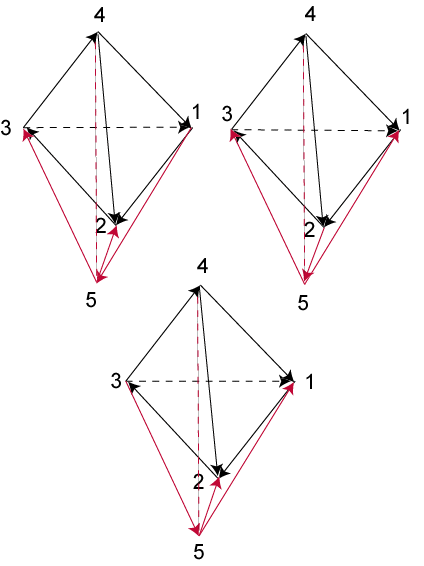 рис. 9
рис. 9
На этом
рисунке вершины 1-4 соответствуют правилу обхода по кресту
(крещение), а соединения в вершине 5 приведено 3 варианта. Во всех вариантах
векторы устремлений соответствуют правилам образования дополнительных
крестов. Например, в верхнем левом рисунке такие кресты образуются взаимодополнительными парами (4,1)-(5,3), (3,4)-(1,5), (3,1)-(5,2).
В этом рисунке векторы
устремлений в вершинах 4 и 5 характеризуются тем, что два вектора в них входит
и один выходит. В разных рисунках они только сдвинуты друг относительно друга
по "фазе". Но замкнутый рисунок
силовых линий образует только нижний рисунок, в котором результирующий
вектор входит в вершину 1.
Еще одна особенность этих
кристаллов заключается в том, что каждый тетраэдр содержит в себе два ребра,
не задействованных в обходе по кресту. Они как бы составляют дополнительный
крест, который формирует "валентные" свойства тетраэдра. Возможно,
что эти вакантные ребра могут участвовать в формировании "силовых уровней" на
более высоких уровнях иерархии. Таких дополнительных взаимосвязей может быть
только три. В этом случае, на первом уровне будут стоять тетраэдры, на
втором - звездные тетраэдры, а третий уровень может стягивать в "тяж" уже сами
звездные тетраэдры.
3.2.
ШЕСТИМЕРНОЕ ПРОСТРАНСТВО
Ïðèâåäåì íåêîòîðûå ñâîéñòâà åùå îäíîãî ïространствà измерений более высокого уровня (6 вершин) образуют 4-х гранную
бипирамиду.
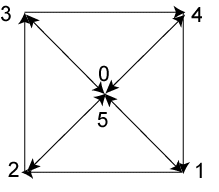 рис.
10
В этой пирамиде обход начинается с
вершины 0, затем по вершинам основания бипирамиды и выходит в вершину 5,
замыкая шестигранник. т.е. такая бипирамида на плоскости образует замкнутый
шестигранник.
Но такая пирамида может иметь и "плоскостное решение". Это пространство может
быт свернуто в Дуаду, состоящую из двух триад, т.е. каждый полюс этой Дуады
будет характеризоваться триединством.
3.3. СЕМИМЕРНОЕ ПРОСТРАНСТВО
Замкнутый
многогранник (пятиугольная бипирамида) может образовывать на плоскости
замкнутую силовую линию -семиконечную звезду (рис.
11).
рис.
10
В этой пирамиде обход начинается с
вершины 0, затем по вершинам основания бипирамиды и выходит в вершину 5,
замыкая шестигранник. т.е. такая бипирамида на плоскости образует замкнутый
шестигранник.
Но такая пирамида может иметь и "плоскостное решение". Это пространство может
быт свернуто в Дуаду, состоящую из двух триад, т.е. каждый полюс этой Дуады
будет характеризоваться триединством.
3.3. СЕМИМЕРНОЕ ПРОСТРАНСТВО
Замкнутый
многогранник (пятиугольная бипирамида) может образовывать на плоскости
замкнутую силовую линию -семиконечную звезду (рис.
11).

ðис.
11
На данном
рисунке приведена двумерная проекция монадного пространства с большей
размерностью, чем предыдущее. В этой двумерной свертке также должен
существовать единственный путь из начальной к конечной вершине. И вполне
возможно, что этот путь указывают стрелки рисунка
(замкнутая "силовая линия", возникшая в момент завершения формирования
монадного семимерного кристалла). Понятно, что такой монадный кристалл будет иметь собственный порядок обхода
вершин, но такой, что свертка этого кристалла в двухмерной плоскости,
возможно, будет совпасть с соответствующими вершинами, обход которых будет
происходить последовательно, по часовой. или против часовой стрелки.
Понятно также и то, что порядок обхода вершин в процессе формирования
монадного кристалла и после завершения такого процесса может быть
разным.
Процесс формирования
монадного кристалла любой мерности будет осущåствляться путем последовательных
обходов по кресту.
Каждый монадный
кристалл имеет собственный порядок порождения вершин (измерений), свой
собственный набор "обходов по кресту".
Главный
вопрос, который возникает при классификации вершин таких кристаллов,
заключается именно в том, чтобы определить местоположение каждого
измерения в общем семействе измерений этого кристалла. При этом в каждом
монадном кристалле высших измерений существуют центрированные двойственные
пары (монады), определяющие соответствующие оси симметрии монадного
кристалла. В икосаэдре таких двойственных пар будет 6 (12 вершин образуют 6
двойственных пар), в додекаэдре 20 вершин образуют 10 двойственных пар.
Преемственность порождения Платоновых тел позволяет говорить о преемственности
собственных пространств, порождаемых Платоновыми телами, что позволяет
производить инвариантные преобразования собственных пространств, осуществляя
соответствующие свертки. или развертки этих пространств. Для
исследователей эти свойства собственных пространств монадных
кристаллов предоставляют возможность трансформировать условия решения той или
иной задачи в более простой вид, осуществляя, например, свертки сложных
собственных пространств, с последующей разверткой после получения решения
задачи.
(Продолжение
следует)
|

 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©