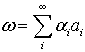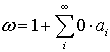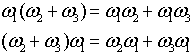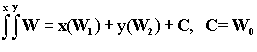2.Концепции

"Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг).

М.И. Беляев, 2015г,©

КОНЦЕПТУАЛЬНЫЕ СИСТЕМЫ

В основу данной страницы положены замечательные идеи В.А. Лефевра ("Конфликтующие структуры", М., "Советское радио, 1973г), которые были использованы для анализа рефлексивных процессов, возникающих в отношениях объект-исследователь. В данной главе делается попытка применить эти идеи для анализа процессов эволюции сложных иерархических систем самой различной природы и, в первую очередь, для анализа сложных интегрированных систем любой природы (технические, социальные, экономические, психические и т.д.).

На странице "О категориях науки" уже упоминалось о том, что символьные формы записи обладают многими замечательными свойствами, которых нет у традиционных форм записи уравнений, ибо символьное мышление отражает в себе Образ объекта и потому уже изначально является более целостным, чем его "знаковые проекции".

Далее, следует обратить внимание, что используемая ниже символьная математика основывается на математике взаимодействия двух тел, ибо в случае взаимодействия трех и более тел они сводятся к двум путем перенормировки и использования символьных операторов.

1. ПЕРСОНАЖИ. КОНЦЕПЦИИ. ПОЗИЦИИ. РОЛИ

Под персонажем системы в самом общем случае будем понимать внешнего или внутреннего оператора (исследователя) системы. Персонаж - это абстракция, так или иначе происходящая из понятия внутреннего исследователя системы, как пространственно локализованного явления, в качестве исходных единиц которого могут рассматриваться отдельные элементы (или подсистемы). Каждый внутренний персонаж имеет свое уникальное имя, свой “внутренний мир”, который для внешнего исследователя можно вначале отождествить с черным ящиком. Под влиянием внешних воздействий черный ящик дает ответную реакцию, которая является индивидуальной для данного черного ящика. Этот ответ на внешнее воздействие с “позиции” черного ящика - персонажа системы фиксируется внешним исследователем, который проводит акт концептуализации и в результате получает некоторую целостную, с его “точки зрения”, с его «позиции», представление о внутреннем персонаже.

Один и тот же персонаж по отношению к вышестоящим уровням иерархии может выступать в роли внутреннего исследователя, а по отношению к нижестоящим уровням – в роли внешнего исследователя. Персонажи в процессе своего функционирования являются источниками и потребителями информации. Рассмотрим некоторую сложную иерархическую систему, в которой в качестве одного из составных элементов – персонажей выступает человек. Очевидно, что такой элемент системы наряду со свойствами, общими для всех элементов данного типа, имеет еще свои специфические свойства, свою индивидуальную смысловую окраску. Именно такое единство общего и специфического даёт исчерпывающее представление о свойствах подобных элементов системы. Действительно, человек наряду со свойствами, необходимыми всем персонажам данной системы для обеспечения ее нормального функционирования, кроме характеристик уровня теоретический и практический подготовки на данном рабочем месте, имеет ещё свои собственные особенности, свою точку зрения (позицию) на задачи и цели функционирования системы, на свою роль и место в системе и т. д.

Совокупность общих и специфических свойств персонажа характеризует его «внутренний мир», его поведение, намерения, взгляды на мир, умозаключения, физические и нравственные ощущения и т. д. Естественно, что совокупность этих общих и специфических свойств влияет на качество функционирования персонажа. Если в системе произойдет отказ одного из элементов типа персонажа, то замена этого персонажа другим может существенно сказаться на качестве функционирования всей системы в целом, т. к. представления персонажей о системе и её состоянии существенно зависит не только от уровня их теоретической и практической подготовки, но и от их личной точки зрения на систему, на выполняемые ею функции, цели и задачи.

Другая особенность персонажей заключается в том, что они в определенные моменты времени, определяемые особенностями функционирования системы, производят “осознание” текущего состояния системы (самостоятельно или под влиянием управляющих воздействий) и в зависимости от этого вырабатывают свои исполнительные действия. Естественно, что подобные «осознания» системы персонажами осуществляется в соответствии со свойствами, которыми данный персонаж обладает и которые проявляются в процессе его функционирования в виде некоторого набора элементарных “актов”, к которым можно свести все действия персонажей в процессе “осознания” ими своего места и роли в системе.

Будем говорить, что набор «актов осознания», с помощью которых данный персонаж «строит» свои отношения с окружающим его миром, составляет концепцию персонажа.

Таким образом, концепция персонажа - это совокупность общих и специфических свойств, которые концептуализируются (отражаются, осознаются) в наборе некоторых правил идентификации и “актов”, которыми в ходе функционирования пользуется тот или иной персонаж.

Формально концепция персонажа не содержит базового множества элементов (объектов), а содержит лишь набор некоторых имен отношений {Rx} и свойств {Ax} персонажа, отражающих его «внутренний мир». Эта концепция материализуется лишь тогда, когда появляется базовое множество элементов, между которыми существуют реальные отношения. В тот момент, когда появляется некоторое базовое множество и концепция проявляется как некоторая реальность, мы будем иметь уже не концепцию, а модель персонажа, действующего на некотором плацдарме, задаваемом базовым множеством. Поэтому можно сказать, что концепция персонажа отражает структуру его модели, что каждая конкретная модель персонажа есть одна из возможных реализаций его концепции. Если модель персонажа реализуется на множестве элементов определённой природы, то концепция персонажа представляет собой некоторую абстрактную категорию, с точки зрения которой неважно, из чего состоит несущее множество модели и какова реальная природа этих отношений на этой модели.

Концепция персонажа несёт в себе важную информацию о самой модели персонажа. Во-первых, по ней легко установить, сколько отношений в данной модели. Во-вторых, узнать арность этих отношений, т.е. имена отношений характеризуют «валентность” реальных отношений.

Наличие концепций у персонажей позволяет говорить об одноименных отношениях в разных моделях персонажей. Выше уже отмечалось, что главная особенность концепции состоит в том, что здесь нет никакого базового множества.

Что же такое реализация концепции? Очевидно, что это уже модель персонажа, в которой есть всё, что и в концепции и, кроме того, появляется базовое множество. Поскольку каждый символ отношения в концепции приобретает реальное содержание, т. е. превращается в отношение на заданном базовом множестве, то при подстановке реальных отношений в ту или иную аксиому концепции она становится либо истинной, либо ложной для этой модели персонажа. Концепция - это в сущности идея, воплощаемая в своих моделях, даже если модель персонажа есть математическая абстракция, всё равно она более «материальный» объект, чем содержащаяся в ней концепция. В модели персонажа есть реальное множество, на котором заданы соответствующие отношения и выполнены требуемые свойства.

Концепция персонажа, как правило, не является неизменной с течением времени. В результате «общения» с другими персонажами она эволюцирует. Этот процесс взаимодействия в общем виде можно описать следующим образом. Предположим, что каждый действующий персонаж системы способен в некоторые определённые моменты времени производить акты «осознания» состояния системы со своей точки зрения (с точки зрения своей концепции).

Тогда в процессе реализации этих актов происходит:

1. Оценка обстановки (состояния системы) и уяснение цели осознания, в результате подобной оценки появляется некоторое базовое множество элементов и действующих персонажей системы. В результате уяснения цели осознания из концепции персонажа выбирается некоторая совокупность имен отношений, аксиом и теорем, которые ставятся в соответствии (связываются) с реальными элементами системы.

2. Оценка замысла (цели функционирования). Используя аксиомы и теоремы, персонаж осуществляет оценку цели своего функционирования. Эта оценка зеркально отражает его позицию, роль и место в системе.

З. Принятие решения. Здесь имена отношений связываются с аксиоматикой и реальными отношениями на реальном базовом множестве в соответствии с целью своего функционирования. Это означает, что используемые при этом имена отношений, теорем наполняются реальным смыслом и персонаж готов действовать, т. е. получена некоторая частная модель персонажа. Таким образом можно сказать, что решение является реализацией некоторой частной концепции персонажа.

4. Реализация решения. Принятое персонажем решение передаётся затем другому персонажу или элементу системы в форме директивы на управление или в форме доклада об исполнении директивы (решения).

Следует заметить, что во многих случаях принятое решение (директива) доводится до персонажа, для которого оно предназначена не полностью, т. е. доводится только в «части, касающейся» данного персонажа, что в директиве на управление персонаж получает не всю необходимую ему информацию. Поэтому сама директива является некоторой частной концепцией, навязанной персонажу для реализации. И персонаж отражает в ней свою позицию и роль.

Из определения частной концепции следует, что передачу своих «взглядов» персонажи могут осуществлять и на уровне имён отношений. Семантика переданных отношений каждым персонажем может определяться в таких случаях индивидуально. Поэтому вполне естественно, что nepcoнаж, «впитавший» в себя некоторую частную концепцию, может вложить в неё собственный смысл, связав её с некоторым базовым подмножеством, отличающимся от базового подмножества, имеющегося у персонажа, принявшего решение и передавшего его для исполнения.

Естественно, что и модель персонажа, принявшего решение для реализации, будет отличаться от модели, имеющейся у персонажа, принявшего такое решение. В результате такого взаимодействия могут получаться частные модели, искажающие процессы функционирования. Такая ситуация чаще всего появляется там, где недостаточно отработано взаимодействие между персонажами, или в результате недостаточной квалификации того или иного персонажа. В результате проб и ошибок, по мере накопления знаний и опыта, персонажи приобретают общие отношения, эти отношения приобретают сходный смысл, определяются целями функционирования персонажей и всей системы в целом. Это значит, что вначале все подобные системы должны иметь определенную информационную избыточность, такую, которая позволила бы из “шумов” извлекать требуемую информацию, имеющую определенный системный смысл. По мере совершенствования функций персонажей требования к избыточности уменьшаются. В процессе взаимодействия, совершенствования этого взаимодействия, директивы будут содержать всё меньше информации, точнее только самую существенную информацию, т. к. вся другая информация будет избыточной, она имеется уже у персонажей. Поэтому концепции будут уже сходными в качественном и количественном отношениях. В зависимости от того, какова природа базового множества, каковы свойства базовых элементов, какой семантический смысл они несут, модель персонажа в зависимости от этого будет иметь и соответствующую семантику. Так, если базовые элементы будут функциональными, то и модель персонажа также будет иметь, прежде всего, функциональный аспект. Если же базовые элементы - суть информационные объекты, то мы будем иметь чисто информационную модель персонажа. Если же базовые элементы несут в себе только структурную нагрузку, то соответствующий аспект будет содержать и модель персонажа. Однако в любом случае в модели будут существовать отношения субординации и координации, а это значит, что любая модель персонажа всегда будет содержать в себе структурный, иерархический аспект.

2. КОНФЛИКТУЮЩИЕ ПЕРСОНАЖИ.

Особый и самостоятельный интерес представляет исследование взаимодействия персонажей в условиях конфликта, который всегда имеет двойственный, а часто и антагонистический характер [В.А. Лефевр]. Он пишет, что проникновение в замысел партнера, т. е. анализ его состояния с его позиций, представляет значительный интерес. При этом особый интерес представляет случай взаимодействия двух объектов, характер взаимоотношений которых является конфликтным, в силу их двойственных свойств. В этом случае само объективное положение дел вынуждает действующие персонажи стать исследователями внутреннего мира своих противников, проводить анализ их “мыслей” и строить свою теорию поведения. Такие поступки дуальных персонажей представляют собой обычные случаи, при попытках достичь в конфликтах взаимопонимания, когда каждая из конфликтующих сторон пытается свои поступки дополнительно проанализировать с позиции противоположной стороны.

Подобное взаимодействие можно характеризовать как использование противоположными сторонами принципа минимакса, который, как это будет показано в дальнейшем, играет исключительно важную роль в двойственных и мультидвойственных отношениях. Если взаимодействие этих персонажей носит устойчивый характер, то это значит, что персонажам известен внутренний мир друг друга, что имеет место зарождение новой интегрированной системы с внутренней двойственностью, характеризующейся отношениями сотрудничества. Конфликты же всегда разрушают такое сотрудничество, и отношения сотрудничества вырождаются в отношения соперничества (антагонизм).

3. КОНЦЕПТУАЛЬНЫЕ СТРУКТУРЫ

Концептуальные структуры - это система вложенных друг в друга (частично или полностью) подструктур. Каждая последующая подструктура (надструктура) порождается от предшествующей с помощью некоторого набора правил идентификации. Совместно с набором правил идентификации, на основе которых могут строиться новые концептуальные структуры - “концепты” произвольной сложности, они образуют формальную теорию концептуальной зависимости.

Концептуальная структура - понятие более абстрактное, чем семантическая структура. Концептуальная структура приобретает четкий прагматический смысл только после определения ее синтаксиса и семантики, когда будет определено базовое множество элементов. Именно совокупность семантических и синтаксических правил идентификации образует некоторую новую, целостную, обладающую качественно новыми свойствами смысловую структурную единицу.

Концептуальная структура фиксирует только последовательность и структуру процессов и подпроцессов, которые произошли в процессе взаимодействия персонажей.

Вот, собственно, первоначальная идея построения концептуальных структур и концептуальных отношений.

4. ИЗОБРАЖЕНИЕ КОНЦЕПТУАЛЬНЫХ СИСТЕМ

Рассмотрим некоторые наборы “примитивных” (элементарных) действий, или актов, к которым в ходе анализа или синтеза концептуальной структуры можно свести все действия, описывающие свойства отдельных ее элементов и подструктур.

Обозначим взаимодействующих персонажей символами Х, У, Z. Чтобы принять решение, X должен построить модель ситуации (например, особым образом схематизировать систему W - плацдарм, на котором происходит взаимодействие персонажей). В свою очередь, У также строит некоторую модель ситуации, но, кроме того, он может осознать, что у его персонажа Х есть некоторая модель ситуации. В свою очередь, Z может осознать, что внутренний мир X и У устроен именно таким образом. Успех в достижении конечной цели функционирования во многом предопределен тем, как персонажи имитируют внутренний мир друг друга, насколько они доверяют друг другу. Не имея детализированной картины, в которой учитываются особенности концептуального строения внутреннего мира взаимодействующего персонажа, невозможно правильно толковать его действия. Например, некоторое изменение состояния системы в условиях помех может быть принято как помеха и не принято к исполнению, в то время как это было действительное изменение состояние системы, которое персонаж должен был принять к сведению и исполнению.

Однако даже при небольшом числе участников концептуальные процессы имеют сложное строение, и необходим специальный аппарат, позволяющий сделать их предметом анализа. Поэтому целесообразно ввести специальный “алгебраический язык”, который позволяет изображать подобные процессы любой сложности. Будем изображать символом W “плацдарм”, на котором действуют персонажи. Картины этого плацдарма, которые могут лежать перед персонажами X, Y и Z, обозначим соответственно

Wх= х (W), Wу = у(W),Wz = z (W)

(читается: “W с позиции Х”, “W с позиции У”, “W с позиции z”). Элементы х (W), у (W), z (W) возникают как результат осознания соответствующим персонажем своего места и роли на плацдарме W. Картины, которые есть у одних персонажей, могут отражаться другими персонажами. В результате возникают элементы Wху, Wхz, Wуz и т. д. (читается: “Wх с позиции У”, “Wх с позиции Z, Wу с позиции Z и т. д.”).

Дадим этим элементам комплексную интерпретацию.

рис. 1

Данный рисунок уже отражает правила трансформации исходного плацдарма системы в результирующий, который формируется после реализации концепции, в результате "зеркального сложения" реализованного решения и исходного плацдарма. В результате такого обхода по "кресту" возникает уже не линейная, а пространственная форма эволюции концепции персонажа.

Теперь можно представить и более сложные схемы концепций, концепции персонажей. Так, элементы с двумя индексами также могут отражаться, в результате чего возникают Wхуz, Wхzу, Wzху и т. д. Они читаются соответственно- “Wху с позиции z” и т. д, и отражаться уже в многомерном собственном пространстве, формируя собственный "кристалл" концепции.

Кристалл потому, что эволюция концепции будет происходить строго последовательно, от одной вершины такого кристалла к другому, ступеньками, как и в естественных кристаллах.

Картина, которую некоторый персонаж имел в момент t₁, может быть также осознана им, уже в момент t₂, причем осознана именно как картина, а не как некоторая “физическая реальность”. Вследствие этого возникают элементы типа Wхх, Wуу, Wххх и т.д. Таким образом, возникает "замкнутый круг" эволюции концепции персонажа, который отражается на рис. 1.

Теперь изобразим процесс взаимоотношения трех персонажей на плацдарме. В момент t₀ в нашей модели никаких внутренних картин у персонажей нет (рис.1). Системе в этом случае соответствует символ W.

Концептуальную систему в момент t₁ можно представить в виде суммы

W1=(W+ х (W))

На рисунке 1 эта ситуация отражается в первом и втором квадрате. Правая часть отражает слагаемые, из которых складывается концептуальная система. Она содержит две компоненты: плацдарм и карту плацдарма, лежащую перед Х. Левая часть W1 представляет уже собой целостную концепцию персонажа .

Если в момент В момент t ₂ осознание этой системы произведет персонаж У, то мы получим следующую картину, которой соответствует следующий многочлен:

W2== W1+ у (W1) =W + х (W)+ у (W+х (W)).

Сумма, находящаяся в круглых скобках, это “W+х (W) с позиции У”. Здесь концепция W1 является уже "единичной", не структурируемой, с позиции У.

Аналогично, концептуальную систему после того, как очередное осознание произвел персонаж Z, мы теперь легко можем изобразить так:

W3= W+ х (W) + у(W+ х (W))+z(W+ х (W) + у(W+ (W)))

Представляется естественным ввести относительно правого индекса закон дистрибутивности, который позволит раскрыть скобки. Например, следующие выражения будут эквивалентными:

W+ х(W) + у(W+х(W))=W+ х (W) + у (W) + у(х (W))

Этот закон может быть интерпретирован двумя способами. Вынесение индекса за скобку можно рассматривать с позиции “внешнего исследователя”. В этом случае внешний исследователь “выделяет” с помощью этой операции “внутренние миры” отдельных персонажей; тем самым получает возможность рассматривать внутренние миры в их целостности. Но из этого не следует, что у самих персонажей есть целостная картина. И эта двойственность хорошо иллюстрируется структурой концепции, ее левой и правой частью. Левая часть является сверткой правой части и характеризует целостность концепции.

С другой стороны, вынесение индекса можно рассматривать именно как возникновение у персонажа картины, т. е. это некоторая операция, происходящая “внутри” персонажа. Обратим внимание на то, что это изображение не позволяет получать информацию об адекватности отражения персонажами картин, лежащих перед другими персонажами. Например, пусть мы имеем два члена Wх и Wху. Персонаж У может иметь как адекватное отражение Wх, так и принципиально не адекватное. Символика регистрирует лишь факт “существования” такого члена во внутреннем мире персонажа У. Поэтому при употреблении символики необходим специальный комментарий, характеризующий степень неадекватности с позиции внешнего исследователя. Введенный таким образом формализм позволяет подходить к анализу персонажей (объектов, событий, явлений, процессов и т. д.) с иерархической точки зрения, например, к анализу “духовной” оболочки живых организмов и т.д.

5. ОПЕРАТОРЫ КОНЦЕПТУАЛИЗАЦИИ

Теперь мы введем специальный формализм для фиксации процесса концептуализации. Для этого мы должны найти формальный способ изображения перехода от выражения W1 к выражению W2, от выражения W2 к выражению W3, и т. д. Многочлены, которые были введены, существенно отличаются от “обычных” многочленов с вещественными коэффициентами. Поэтому необходимо строго ввести тот алгебраический объект, с которым мы будем иметь дело в дальнейшем. Исходными для построения формализма (для трех персонажей) являются символы х, у, z, W и 1, а также круглые скобки “(” и “)”. Из этих символов составляются “слова” — конечные последовательности символов, например, х, х(у(W)), х (W), x(y(z(W))) и т. д. Два слова считаются эквивалентными, если они отличаются только числом вхождения в них символа 1 (например, 1x(1y(1z(1W))) = x(y(z(W))) . Таким образом, символ 1 можно вычеркивать из слов. При этом будем считать, что символы группируются в слова с помощью аддитивной операции сложения, выражающей отношения координации между символами, и мультипликативной операции умножения, символизирующей отношения субординации между символами. С помощью этих же операций слова могут группироваться в высказывания, высказывания в предложения и т. д., образуя сложную иерархическую структуру отношений.

Условимся пока рассматривать слова, не содержащие символа W. Множество всех таких слов счетно. Перенумеруем их некоторым произвольным образом. Получим последовательность а_i. Теперь мы можем ввести понятие концептуального многочлена. Концептуальным многочленом мы будем называть символическую сумму

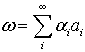где а_i- элемент булевой алгебры, состоящей из двух элементов 0 и 1.

При заданной нумерации а_i многочлен однозначно задается набором коэффициентов а_i. Условимся в дальнейшем выписывать лишь те члены, коэффициенты перед которыми равны 1. Необходимо обратить внимание на отличие многочлена от отдельного слова. Если мы пишем, например, w =1, то это значит, что рассматривается многочлен

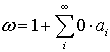В котором только перед а_i=1 коэффициент отличен от нуля. Теперь можно ввести операции сложения и умножения многочленов. Они вводятся так же, как и операции над “обычными” многочленами, с той лишь существенной разницей, что умножение оказывается не коммутативным. Нетрудно видеть, что умножение ассоциативно и выполняются правый и левый законы дистрибутивности:

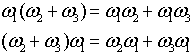Каждому многочлену W поставим в соответствие специфический многочлен W=w (W). Многочлены W, как мы показали раньше, позволяют изображать состояния концептуальных систем, а многочлены w будут интерпретированы как операторы концептуализации.

Теперь мы можем выразить на алгебраическом языке процедуры трансформацию концепций персонажа Х. Для этого необходимо многочлен W, выражающий исходный плацдарм системы умножить справа на многочлен 1+х. Результатом такого умножения будет многочлен W₁= (1+x) (W)=W+x(W) , ..., Wn= (1+x) (W_n-1)

Если же теперь умножим многочлен W₁ справа на многочлен 1+у получим состояние W₂.

W₂=(1+х)(1+у) (W)=W+х (W)+у(W+х (W))

Состояние W_зпорождается умножением W₂ справа на 1+у

Wз = (1+x)(1+y)(l+z) (W)=W+x(W)+(W+x(W))y+ z (W+x(W)+y (W+x(W)))

Таким образом, той процедуре осознания, которую мы изобразили графически (она представляет собой схематизацию естественно – интуитивного понимания рефлексии), соответствует теперь алгебраическая операция умножения многочлена на многочлены 1+х, 1+у, 1+z. Мы только что описали случай, когда персонажи производят осознание последовательно. Но легко изобразить и случай, когда осознание производят все три персонажа одновременно.

Оператор концептуализации будет таким:

ω = 1 + х + у + z,

а эволюция многочлена, характеризующего состояния концептуальных систем, выразится соотношением

Wn= (1+x+y+z)(W)=ωW,

где п - число концептуализаций.

Подобное изображение процессов осознания значительно расширяет возможности исследования более сложных типов концептуализации. Нетрудно видеть, что простейшему оператору концептуализации w= 1 +х будет соответствовать случай, когда процесс концептуализации производит один и тот же персонаж через определенные промежутки времени. Этот процесс можно представить следующими многочленами.

W_n = Wω_n=W (1+x)ⁿ,

где п - число концептуализаций.

Особый интерес для нас будет представлять оператор концептуализации вида ω =y= 1 - х;

Перепишем его в виде 1=х+у.

6. КОНЦЕПТУАЛЬНЫЕ ОБОЛОЧКИ

Инвариантность типа многочлена по отношению к оператору концептуализации может быть выражена следующим очевидным тождеством:

(1+ω) (W+ ω(W)) =W+ ω(W),

где W= W + ω(W) - многочлен, характеризующий концептуальную оболочку оператора концептуализации. Каждая концептуализация системы с помощью инвариантного оператора приводит к увеличению уровня иерархии системы, в которой иерархическая система предыдущего уровня иерархии может рассматриваться как подоболочка W= W + ω(W), а член w(W) будет характеризовать появление новой уникальной подоболочки.

Такая подоболочка является нормированной (единичной), а далее процесс повторяется, по образу и подобию, т.е. всякий раз, когда производится осознание состояния системы, осуществляется процесс ее самонормировки и приведение системы к единичной подоболочке, которая затем может использоваться для строительства более сложной оболочки. Процессы самонормирования подоболочек порождают свойства инвариантности операторов концептуалтизации.

Инвариантность оператора концептуализации проявляется в том, что даже при многократном применении он оставляет структуру многочлена неизменной: каждый последующий член ряда является суммой двух его последних членов. Таким образом, инвариантные операторы порождают класс инвариантных концептуальных оболочек и подоболочек.

Рассмотрим несколько примеров операторов концептуализаций.

1. Оператор ω = 1+x². При однократном применении он порождает многочлен

W₁=W+ xx (W)=W+ x(x (W))

Перед персонажем Х лежит не плацдарм W, а картина этого плацдарма, отраженная им самим (зеркальное отражение). Реальность W с позиции персонажа Х всегда выступает лишь как элемент его внутреннего мира. Осознание своего подлинного состояния W₁посредством оператора ω = 1+х вновь приводит к такому же типу внутреннего мира, т.е. тип этого внутреннего мира замкнут относительно данного оператора. Действительно,

(1+x²) (W+x(x (W))) = W + x(x(W))

Оператор осознания 1+x² обрекает персонажа вступать в отношение с реальностью лишь как с элементом своего внутреннего мира.

2. Оператор ω=1+x+x². Персонаж, “вооруженный” таким оператором, производит двойную концептуализацию.

Выбирая тот или иной оператор концептуализации, мы имеем возможность получать различные отражения внутренних миров персонажей, различные иерархические структуры, различные концептуальные оболочки и подоболочки. Из определения концептуальных оболочек, которые формируются с использованием инвариантных операторов концептуализации, следует, что такие оболочки и подоболочки являются замкнутыми и структурно ограниченными.

Более подробное изложение, связанное со взаимодействием персонажей, "исповедующих" тот или иной оператор концептуализации, приведен в монографии "Милогия".

Данные примеры показывают, что символьная математика, использующая биномиальные многочлены более глубоко отражает смыслы отражаемых этими тождествами процессов. Так, последовательность процессов концептуализации характеризуется цикличностью, эти процессы носят рекуррентный характер. Так, вынося символ за скобки, мы получим

W₁= W₀ (1+ x )

т. е. процедуре осознания системы персонажем Х соответствует алгебраическая операция умножения структурного многочлена на многочлен 1+х. Проводя формальные преобразования полученных таким образом структурных многочленов, мы будем получать концептуальные структуры разной степени сложности. В случае взаимодействия двух и более персонажей мы будем иметь дело со структурными многочленами с двумя и более «переменными». В этом случае мы будем говорить о позиции того или иного персонажа с точки зрения другого и получать концептуальные структуры, отражающие процессы взаимодействия этих персонажей.

Произвольный структурный многочлен, фиксирующий взаимоотношения, например, двух персонажей, в моменты времени t₁ и t₂ можно свести к виду:

W=W₀+х(W₁)+ у(W₂)

а осознание понимать как отражение всей ситуация одним внешним персонажем. Пусть, например, акт осознания произвёл Х. Вся система изменилась: «внутри» персонажа Х оказался многочлен W, а персонаж У и W₀остались неизменными. Таким образом, система перешла в состояние

x (W) =(W₀+(W₁)x + W₂)у)x +(W₂)у+W₀

Эта процедура напоминает нахождение формальной первообразной и её можно обозначить соответствующим образом:

Аналогично

В качестве константы С выступают члены, не имеющие крайним правым индексом имени персонажа, который производит осознание. В случае, когда осознание производят оба персонажа одновременно

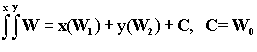Можно ввести и операцию, обратную интегрированию, - нахождение частной производной. Её можно истолковать двояко. С одной стороны, ее можно понимать как выделение внутреннего мира персонажа, с другой стороны, - как нахождение состояния системы, предшествующего акту осознания, конечно, при условии, что данное состояние системы было порождено актом осознания персонажа в указанном выше смысле.

Формально операцию дифференцирования можно определить так

Если многочлен W₁ представим в виде

W₁=W₂+х(W₃)+у(W₄)

то можно найти вторую производную, т. е. извлечь внутренний мир соответствующего персонажа, лежащий внутри уже извлеченного внутреннего мира:

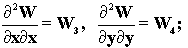Процедуру дифференцирования можно проводить до тех пор, пока очередная производная не примет значения 0. Рассмотрим ещё один пример. Рассмотрим процессы взаимодействия персонажа Х с персонажем У. Пусть в момент t0 персонаж Х никаких отображений о состояния персонажа У не имеет. Тогда о персонаже У него будет только первоначальное, статическое представление, определяемое рамками функциональных отношений. Изобразим это состояние символом у(W₀). Представим теперь, что в момент времени t1 персонаж Х произвёл осознание персонажа У. Тогда можно записать

W₁=(1+х) у(W₀)=1(у(W₀)+х(у(W₀)))

Данная символическая сумма содержит две компоненты: статическое представление персонажа - у(W₀) и его образ, отображённый персонажем Х в момент t₁ . Тогда в момент t₂ получим следующий многочлен:

W₂=(1+х) W₁=(W₁+х(W₁))=1(у(W₀)+х(у(W₀))+х(у(W₀)+х(у(W₀)))

Или, используя инвариантные преобразования, рассмотренные выше, мы получим следующие структурные цепочки

W₂=ωW₁₌ω(W₀+х(W₀))

Проводя подобные сворачивания, мы получим цепочку

W₃=W₂=ωW₂=ω(W₁+х(W₁))=ωW₁

Далее аналогично

W₃=ωW₂;

W₄=ωW₃

W₅=ωW₄;

Из вышеизложенного видно, что сложность структурных многочленов характеризуется строгой преемственностью вида

Поясним теперь возможный смысл операции вынесения символа персонажа за скобки. Это может означать процесс формирования цельной структуры некоторого образа системы. Отметим, что вынесение символа за скобки можно рассматривать и с позиции «внешнего» исследователя, который с помощью этой операции выделяет внутренние образы персонажа, имеющиеся у него в тот или другой момент времени и, тем самым, получает возможность рассматривать эти внутренние образы во всей их целостности. Следует сказать, что и у персонажа системы могут возникать целостные картины о состоянии системы, но только с его «точки зрения». Именно поэтому внешний исследователь и персонаж могут иметь различные представления о системе, даже в том случае, если их внутренние образы будут описываться одними и теми же концептуальными структурами. Символика лишь регистрирует факт существования подобных отображений у внешнего исследователя и персонажа, но не отражают внутренней сущности их системных представлений. Из этого факта (и повседневный опыт подтверждает это) следует, что для полного представления о системе недостаточно только одного представления об объекте исследования. Задачу возможно решить только при использовании разных системных представлений, связанных друг с другом. Причём элементы, на которые расчленяется система, могут быть различными в разных системных представлениях, т. е. иметь различный семантический смысл, иметь разное синтаксическое и семантическое описание.

Объект как бы проектируется на разные оси координат п-мерного пространства, порождая тем самым определённые упорядоченные структуры относительно выбранных «осей координат». Ясно, что в этом случае, даже если эти структуры будут иметь разный семантический смысл, проекции объекта будут связаны между собой, поэтому исследователь имеет возможность анализировать различные представления образа объекта, минуя сам объект. Например, в вычислительной технике используется определённый набор системных представлений объекта: блок-схема, принципиальная схема, монтажная схема и т. д. Такое членение на части в совокупности и даёт исчерпывающее представление об объекте, хотя при этом оказывается невозможным ответить на самый простой вопрос о том, из каких элементов состоит объект, если не указать, каким системным представлением следует пользоваться.

Таким образом, можно сказать, что концептуальные структуры, возникающие у того или иного персонажа в процессе функционирования, есть некоторое системное представление об объекте и его состоянии. Естественно, что эти системные представления могут быть различными у каждого персонажа. Эти системные представления могут пересекаться, а могут и не пересекаться друг с другом. Даже в том случае, когда персонажи будут иметь одну и ту же структуру образов, эти системные представления у них могут быть различными вследствие различных описаний семантики этих образов.

8. ЗАДАЧА ВОССТАНОВЛЕНИЯ ИСТОРИИ ФОРМИРОВАНИЯ МНОГОЧЛЕНА

Алгебраический подход к концептуальным структурам порождает некоторые специфические задачи. Например, возникает вопрос: может ли система, находящаяся в состоянии W1 посредством “срабатывания” некоторого оператора концептуализации перейти в состояние W2. Ответ на вопрос сводится к решению задачи о существовании решения уравнения ω(W₁)=W₂.

Это линейное относительно ω уравнение может иметь не единственное решение, а может не иметь решения вообще. Например, уравнение

(1+х) ω = 1 + х + х² + х³

имеет два решения ω₁=1+x+х² ω₂=1+х² , а уравнение (1+х)ω=1+х³не имеет решений.

До сих пор мы предполагали, что персонаж наделен лишь одним оператором концептуализации. Теперь мы откажемся от этого предположения и позволим персонажу иметь набор операторов. В рамках нашего специального построения можно поставить вопрос о восстановлении “истории” формирования определенного состояния W. Для этого необходимо представить W в виде произведения сомножителей

Wn=ω_n... ω₃ ω₂ ω₁ (W)

Естественно, что в силу неоднозначности разложения мы можем получить не одну, а некоторое множество траектории, т. е. последовательностей, в которых “срабатывали” операторы, порождая это состояние. Особый интерес представляет вопрос о разложении многочленов на неприводимые множители - многочлены. Неприводимыми мы называем многочлены, которые нельзя представить как произведение двух многочленов, каждый из которых отличен от 1.

Неприводимыe сомножители можно интерпретировать как “элементарные” акты концептуализации. Заметим, что в построенном исчислении не будет справедлива теорема о единственности разложения на неприводимые множители. Например, многочлен ω=1+х+х²+х³ представим двумя следующими способами:

ω=(1+х)³ = (1+х)(1+х²).

Конечно, подобное “восстановление истории” имеет смысл лишь - в рамках данной модели со всеми принятыми ограничениями, самым существенным из которых является то, что аналогом акта концептуализации выступает некоторый множитель. Изложенный здесь способ “восстановления истории” представляет собой частный и простейший случай, однако он иллюстрирует сущность проблемы. Задача восстановления “истории эволюции” структурных многочленов в определенной мере может быть и упрощена, если учитывать свойства сенсорных оболочек в замкнутых структурах, т. е. в таких структурах вход в систему и выход из нее осуществляется через ее сенсорные подоболочки.

РЕЗЮМЕ

Содержание страницы имеет важное значение для единой теории эволюции иерархических систем.

1. Введение понятия персонажа системы, его концепции и операторов концептуализации дают простой и наглядный метод для формального описания процессов эволюции иерархических систем самой различной природы в виде многочленов, которые автор называет концептуальными. Операторы концептуализации, отражающие “внутренний мир” того или иного персонажа, позволяют формализовать процессы последовательного изменения внутренней сущности этих персонажей.

2. Типы многочленов, порождаемые подобными операторами, могут быть различными. Оператор концептуализации, применяемый последовательно к концептуальному многочлену, является инвариантным по отношению к этому многочлену и порождает специальный класс инвариантных концептуальных оболочек и подоболочек, которые, как это будет показано в дальнейшем, имеют важное значение при многоуровневом описании процессов эволюции персонажей иерархических систем.

3. Концептуальные многочлены имеют исключительно важное значение для понимания основ теории инвариантных преобразований собственных иерархических пространств. Так, например, принимая в качестве базисного персонажа системы атом водорода, мы получаем возможность, используя базисные «аксиомы и теоремы», получить концептуального описания подоболочек и оболочек Периодической системы химических элементов.

4. Концептуальные структурные многочлены позволяют понять принципы формирования фракталов, изучению которых в современной науке уделяется самое пристальное внимание.

e-mail:

С благодарностью приму все ваши замечания, предложения,

с признательностью отвечу на ваши вопросы

Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать о всех замеченных ошибках, некорректных формулировках.

Книги "Основы милогии", "Милогия" могут быть высланы в Ваш адрес наложенным платежом,

URL1: milogy.net

e-mail: [email protected]

Карта сайта

rss

Карта