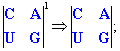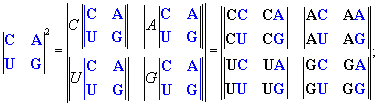|
СПИНОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
1.
СПИНОРНОЕ ИСЧИСЛЕНИЕ
1.1. ОСНОВЫ
ТЕОРИИ
Спинорное исчисление [БСЭ:
Румер Ю. Б., Спинорный анализ, М. - Л., 1936; Картан
Э., Теория спиноров, пер. с франц., М., 1947; Ландау Л., Лифшиц Е.,
Квантовая механика, ч.1, М. — Л., 1948 (Теоретическая физика, т. 5, ч. 1 );
Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967;
его же, Теория спиноров, «Успехи математических наук»,
1955, т. 10, в. 2(64)].
Это математическая теория,
изучающая величины особого рода -
спиноры. При изучении физических величин их относят обычно к той или иной
системе координат. В зависимости от закона
преобразования этих величин при переходе от
одной системы координат к другой различают величины различных
типов (тензоры, псевдотензоры). При изучении явления спина электрона
было обнаружено, что существуют физические
величины, не принадлежащие к ранее известным типам (например, эти величины
могут быть определены лишь с точностью до знака, т. к. при повороте системы
координат на 2 вокруг некоторой оси все компоненты этих величин
меняют знак). Такие величины были рассмотрены ещё в 1913
Э.
Картаном в его исследованиях по теории представлений групп и вновь открыты в
1929 Б. Л. Варденом в связи с исследованиями по квантовой механике. Он
назвал эти величины спинорами.
Спиноры первой валентности задаются двумя комплексными числами
вокруг некоторой оси все компоненты этих величин
меняют знак). Такие величины были рассмотрены ещё в 1913
Э.
Картаном в его исследованиях по теории представлений групп и вновь открыты в
1929 Б. Л. Варденом в связи с исследованиями по квантовой механике. Он
назвал эти величины спинорами.
Спиноры первой валентности задаются двумя комплексными числами
 ,
причём в отличие, например, от тензоров, для которых различные совокупности
чисел задают различные тензоры, для спиноров считают, что совокупности ,
причём в отличие, например, от тензоров, для которых различные совокупности
чисел задают различные тензоры, для спиноров считают, что совокупности
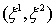 и и
 определяют
один и тот же спинор. Это объясняется законом преобразования спиноров при
переходе от одной системы координат к другой. При повороте системы координат
на угол определяют
один и тот же спинор. Это объясняется законом преобразования спиноров при
переходе от одной системы координат к другой. При повороте системы координат
на угол 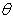 вокруг
оси с направляющими косинусами вокруг
оси с направляющими косинусами
 компоненты
спинора преобразуются по формулам компоненты
спинора преобразуются по формулам
 где
где

 В
частности, при повороте системы координат на угол 2
В
частности, при повороте системы координат на угол 2 ,
возвращающем её в исходное положение, компоненты спинора меняют знак, что
объясняет тождественность спиноров ,
возвращающем её в исходное положение, компоненты спинора меняют знак, что
объясняет тождественность спиноров
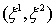 и и
 .
Примером спинорной величины может служить волновая функция частицы со
спином 1/2 (например, электрона).
Матрица .
Примером спинорной величины может служить волновая функция частицы со
спином 1/2 (например, электрона).
Матрица
 является в этом случае унитарной матрицей.
К
спинорам относят и величины
является в этом случае унитарной матрицей.
К
спинорам относят и величины
 ,
компоненты которых комплексно сопряжены с компонентами спинора ,
компоненты которых комплексно сопряжены с компонентами спинора
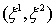 .
Матрица преобразования этих величин имеет вид .
Матрица преобразования этих величин имеет вид
 .
Наряду с
введёнными выше контравариантными компонентами .
Наряду с
введёнными выше контравариантными компонентами
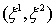 спинора, можно
ввести ковариантные компоненты
спинора, можно
ввести ковариантные компоненты  положив
положив 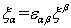 , где , где  (как всегда, по повторяющимся индексам производится суммирование). Иными
словами,
(как всегда, по повторяющимся индексам производится суммирование). Иными
словами,  .
Ковариантные
компоненты преобразуются матрицей .
Ковариантные
компоненты преобразуются матрицей
 .
При вращениях эта матрица совпадает с матрицей .
При вращениях эта матрица совпадает с матрицей
 ,
т. е. при вращениях ковариантные компоненты спинора преобразуются как
компоненты комплексно сопряжённого спинора.
Посмотрите на эту
трогательную симметрию спинорных преобразований и сравните их с симметрией
законов сохранения во вращающемся кресте (Законы
сохранения).
Спинорная алгебра строится
аналогично обычной тензорной алгебре (см. ниже).
Спинором
валентности r (или спинтензором) называется совокупность
2r комплексных
чисел ,
т. е. при вращениях ковариантные компоненты спинора преобразуются как
компоненты комплексно сопряжённого спинора.
Посмотрите на эту
трогательную симметрию спинорных преобразований и сравните их с симметрией
законов сохранения во вращающемся кресте (Законы
сохранения).
Спинорная алгебра строится
аналогично обычной тензорной алгебре (см. ниже).
Спинором
валентности r (или спинтензором) называется совокупность
2r комплексных
чисел 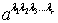 ,
определённых с точностью до знака, которая при переходе
от одной системы
координат к другой преобразуется как произведение r компонент спиноров
первой валентности, т. е. как ,
определённых с точностью до знака, которая при переходе
от одной системы
координат к другой преобразуется как произведение r компонент спиноров
первой валентности, т. е. как
 Аналогично определяются комплексно-сопряжённый
спинор валентности r, смешанный спинор, спинор с ковариантными компонентами
и т. д. Сложение спиноров и умножение спинора на скаляр определяются
покоординатно. Произведением двух спиноров называется спинор,
компонентами которого являются попарные произведения компонент
сомножителей.
Например, из спиноров второй
Аналогично определяются комплексно-сопряжённый
спинор валентности r, смешанный спинор, спинор с ковариантными компонентами
и т. д. Сложение спиноров и умножение спинора на скаляр определяются
покоординатно. Произведением двух спиноров называется спинор,
компонентами которого являются попарные произведения компонент
сомножителей.
Например, из спиноров второй  и третьей
и третьей  валентности можно образовать спинор пятой валентности
валентности можно образовать спинор пятой валентности 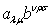 .
Свёрткой спинора
.
Свёрткой спинора
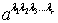 по индексам
по индексам
 и и
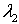 называется спинор называется спинор
 В
спинорной алгебре часто используются тождества
В
спинорной алгебре часто используются тождества

 В
квантовой механике важную роль играет исследование систем линейных
дифференциальных уравнений, связывающих величины спинорного типа, которые
остаются инвариантными при унимодулярных преобразованиях, т. к.
только такие системы уравнений релятивистски инвариантны. Наиболее важны
приложения спинорного анализа к теории уравнений Максвелла и Дирака. Запись
этих уравнений в спинорной форме позволяет сразу установить их
релятивистскую инвариантность, установить характер преобразования входящих в
них величин. Спинорная алгебра находит также приложения к квантовой теории
химической валентности. Теория спиноров в пространствах высшего числа
измерений связана с представлениями групп
вращений многомерных пространств. Спинорное исчисление
связано также с некоторыми вопросами
неевклидовой геометрии.
1.2.
СПИНОРНЫЕ МАТРИЦЫ
Рассмотреннные выше основы спинорного исчисления могут свидетельствовать о
том, что математика далеко продвинулась за "горизонт осознанного мира".
Замечательная симметрия спиноров у физиков не вызывает ни малейшего
удивления. Для них этот феномен -самое обыденное понятие. И тем не менее за
этим феноменом скрывается чудо Единого закона эволюции двойственного
отношения.
Свойства
спиноров раскрывают самые сокровенные тайны Бытия. Они отражают в себе
свойства 4-х вращающихся
"спинорных стихий":
В
квантовой механике важную роль играет исследование систем линейных
дифференциальных уравнений, связывающих величины спинорного типа, которые
остаются инвариантными при унимодулярных преобразованиях, т. к.
только такие системы уравнений релятивистски инвариантны. Наиболее важны
приложения спинорного анализа к теории уравнений Максвелла и Дирака. Запись
этих уравнений в спинорной форме позволяет сразу установить их
релятивистскую инвариантность, установить характер преобразования входящих в
них величин. Спинорная алгебра находит также приложения к квантовой теории
химической валентности. Теория спиноров в пространствах высшего числа
измерений связана с представлениями групп
вращений многомерных пространств. Спинорное исчисление
связано также с некоторыми вопросами
неевклидовой геометрии.
1.2.
СПИНОРНЫЕ МАТРИЦЫ
Рассмотреннные выше основы спинорного исчисления могут свидетельствовать о
том, что математика далеко продвинулась за "горизонт осознанного мира".
Замечательная симметрия спиноров у физиков не вызывает ни малейшего
удивления. Для них этот феномен -самое обыденное понятие. И тем не менее за
этим феноменом скрывается чудо Единого закона эволюции двойственного
отношения.
Свойства
спиноров раскрывают самые сокровенные тайны Бытия. Они отражают в себе
свойства 4-х вращающихся
"спинорных стихий":
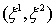 и
и  .
которые могут взамопревращаться друг в друга, формируя рыночное тождество,
отражающего баланс взамиотношений .
которые могут взамопревращаться друг в друга, формируя рыночное тождество,
отражающего баланс взамиотношений
 Это тождество несет в себе природную гармонию отношений
симметрии двойственного отношения (Весы
монады).
Это тождество несет в себе природную гармонию отношений
симметрии двойственного отношения (Весы
монады).
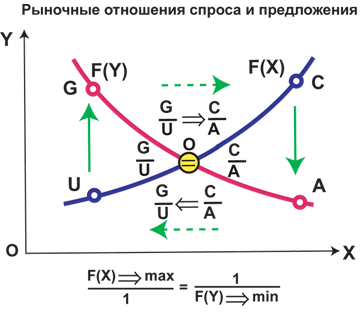 рис. 1
Изображенные на рисунке графики в экономике отражают закон спроса и
предложения на рынке товаров и услуг. Единый закон эволюции двоцссвтеного
отношения позволяет переносить закон спроса и предложения на системы самой
разной природы, включая и физические системы. Поэтому спинорное исчисление
просто обязано отражать в себе равновесность преобразований двойственного
отношения
рис. 1
Изображенные на рисунке графики в экономике отражают закон спроса и
предложения на рынке товаров и услуг. Единый закон эволюции двоцссвтеного
отношения позволяет переносить закон спроса и предложения на системы самой
разной природы, включая и физические системы. Поэтому спинорное исчисление
просто обязано отражать в себе равновесность преобразований двойственного
отношения 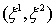 .
Тогда
взаимодополнительные матрицы-спиноры в совокупности
сформируют Единый куб эволюции двойственного отношения .
Тогда
взаимодополнительные матрицы-спиноры в совокупности
сформируют Единый куб эволюции двойственного отношения
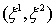 .
Это отношение является спинорной монадой.
Это скорее
метафизическое понятие, чем физическое.
Нетрудно осознать, что тождество на плоскости отображается как крест. В
пространстве трех измерений это будет уже треугольная пирамида. Тогда два
спинорных тетраэдра сформируют звездный спинорный тетраэдр. .
Это отношение является спинорной монадой.
Это скорее
метафизическое понятие, чем физическое.
Нетрудно осознать, что тождество на плоскости отображается как крест. В
пространстве трех измерений это будет уже треугольная пирамида. Тогда два
спинорных тетраэдра сформируют звездный спинорный тетраэдр.
 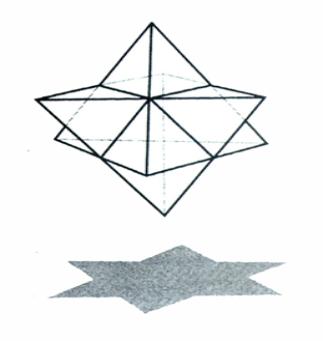
рис.2
Видите, рисунок справа отражает одну из самых сокровенных тайн мироздания:
cимметрия высших измерений сохраняется в их
проекциях на низшие измерения. И эти свойства не могут не отражаться в спинорных
матрицах высших измерений, которые могут свертываться в спинорные матрицы низших
измерений.
В самом общем случае все спинорные матрицы, отражающие эволюцию двойственного
отношения  (S
и S
-
взаимодополнительные "спины"),
можно записать по
образу и подобию Русской матрицы (Русская
матрица).
(S
и S
-
взаимодополнительные "спины"),
можно записать по
образу и подобию Русской матрицы (Русская
матрица).
|
В |
S-4 |
S-3 |
S-2 |
S-1 |
S0 |
S1 |
S2 |
S3 |
S4 |
A* |
|
S8 |
S-4S8 |
S-3S7 |
S-2S6 |
S-1S5 |
S0S4 |
S1S3 |
S2S2 |
S3S1 |
S4S0 |
S0 |
|
L7 |
S-4S7 |
S-3S6 |
S-2S5 |
S-1S4 |
S0S3 |
S1S2 |
S2S1 |
S3S0 |
S4S-1 |
S-1 |
| L6 |
S-4S6 |
S-3S5 |
S-2S4 |
S-1S3 |
S0S2 |
S1S1 |
S2S0 |
S3S-1 |
S4S-2 |
S-2 |
| L5 |
S-4S5 |
S-3S4 |
S-2S3 |
S-1S2 |
S0S1 |
S1S0 |
S2S-1 |
S3S-2 |
S4S-3 |
S-3 |
| L4 |
S-4S4 |
S-3S3 |
S-2S2 |
S-1S1 |
S0S0 |
S1S-1 |
S2S-2 |
S3S-3 |
S4S-4 |
S-4 |
| L3 |
S-4S3 |
S-3S2 |
S-2S1 |
S-1S0 |
S0S-1 |
S1S-2 |
S2S-3 |
S3S-4 |
S4S-5 |
S-5 |
| L2 |
S-4S2 |
S-3S1 |
S-2S0 |
S-1S-1 |
S0S-2 |
S1S-3 |
S2S-4 |
S3S-5 |
S4S-6 |
S-6 |
| L1 |
S-4S1 |
S-3S0 |
S-2S-1 |
S-1S-2 |
S0S-3 |
S1S-4 |
S2S-5 |
S3S-6 |
S4S-7 |
S-7 |
| L0 |
S-4S0 |
S-3S-1 |
S-2S-2 |
S-1S-3 |
S0S-4 |
S1S-5 |
S2S-6 |
S3S-7 |
S4S-8 |
S-8 |
|
A |
S-4 |
S-3 |
S-2 |
S-1 |
S0 |
S1 |
S2 |
S3 |
S4 |
В* |
рис.
3
Эта спинорная матрица
несет в себе многомерные смыслы и отражает проекцию на плоскость ГиперКуба.
Эта матрица обладает магическими свойствами (Магия
чисел).
В
центре матрицы находится магическая энеаграмма, представляющая собой проекцию
трехмерного спинорного пространства (куб) на плоскость
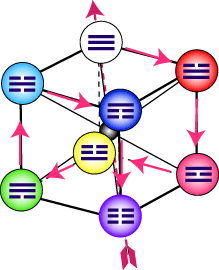 рис.
4
Этот "базисный кубик" вращается в пространств
гиперкуба, формируя спинорный Цветок Жизни ДНК (Цветок
Жизни ДНК).
рис.
4
Этот "базисный кубик" вращается в пространств
гиперкуба, формируя спинорный Цветок Жизни ДНК (Цветок
Жизни ДНК).
 рис.
5
Попытайтесь осознать, как по образу и подобию вращение базисного спинорного
кубика трансформируется в иные "кубики", каждый из которых обладает собственным
"очарованием","красотой" и другими мистическими свойствами, которыми физики
щедро награждают, например, свойства кварков.
Даннаяя спинорная матрица является
матрицей, размерностью 9х9, т.е. она имеет в своем составе 9х9=81 спинорных
чисел.
Если из этой матрицы вычленить 17
чисел, стоящих на главных диагоналях и представляющих собой "нормированные
спиноры", то мы получим 81-17=64 спинорных числа.
В матрице, размерностью 7х7 таких
перенормировочных спиноров будет
13. В матрице 5х5 таких
перенормированных спиноров будет 9,
а матрица размерностью 3х3 является уже базисной спинорной матрицей, формирующей
все собственное пространство спинорной матрицы.
Из анализа свойств
чисел спинорной матрицы следует, что числа, стоящи на главных диагоналях
спинорной матрицы, определяют число ее взаимодополнительных Великих
Пределов.
Важнейшее
свойство спинорной матрицы (рис. 3) заключается в том, что любое спинорное число
этой матрицы может порождать, по образу и подобию, собственную спинорную
матрицу.
Перенормировка спиноров приводит к тому, что они периодически становятся
инвариантными сами себе и начинают отличаться друг от друга только "цветом",
несущим в себе "допплеровское смещение" базисной ориентации спинора. Полагаю,
что уникальные свойства чисел этой матрицы привлекут к себе внимание
ученых многих направлений.
2.
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
2.1.
ОСНОВЫ ТЕОРИИ
[БСЭ:
Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9
изд., М., 1965;
Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд.,
М., 1967; Схоутен Я. А.,
Тензорный анализ для физиков, пер. с англ., М., 1965;
Мак-Коннел А.-Д.,
Введение в тензорный анализ, пер. с англ., М., 1963;
Сокольников И. О.,
Тензорный анализ, пер. с англ., М., 1971.]
Историческая справка.
Возникновение тензорного исчисления было подготовлено
в 19 веке развитием теории алгебраических форм, с
одной стороны, и теории квадратичных дифференциальных форм -
с другой. Исследования в области теории дифференциальных квадратичных форм
были непосредственно связаны с дифференциальной геометрией: с геометрией
поверхностей (К. Гаусс) и с геометрией многомерного
метрического пространства (Б. Риман). Современную форму
тензорному исчислению придал итальянский математик Г. Риччи-Курбастро,
поэтому тензорнон исчисление иногда называется
исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого
распространения. Внимание к ним возросло после появления (1915-16)
общей теории относительности А. Эйнштейна, математическая часть которой
целиком основана на тензорном исчислении.
Тензор
(от лат. tensus -
напряжённый, натянутый), математический термин, появившийся в середине 19 века
и с тех пор применяющийся в двух различных смыслах. Наибольшее
распространение термин «тензор» получил в современном
тензорном исчислении,
где это название присваивается особого рода величинам, преобразующимся по
особому закону. В механике, особенно в теории упругости, термин «тензор»
широко применяется как синоним симметрического аффинора, то есть линейного
оператора Ф, преобразующего вектор х в вектор
Фх, и симметрического в том смысле, что
скалярное произведение уФх
не меняется при перестановке векторов х и у. Здесь термин был первоначально
связан с малыми растяжениями (и сжатиями), возникающими при упругой
деформации (откуда и название «тензор»),
а затем перенесён в другие области механики. Так появились
тензор
деформации,
тензор
напряжения,
тензор
инерции и др.
Тензорное
исчисление,
математическая теория, изучающая величины особого рода - тензоры, их
свойства и правила действий над ними.
Тензорное исчисление
является развитием и обобщением векторного исчисления и теории матриц.
Тензорное
исчисление
широко применяется в дифференциальной геометрии, теории римановых
пространств, теории относительности, механике, электродинамике и других
областях науки. Для описания многих физических и геометрических фактов
обычно вводится та или иная система координат, что позволяет описывать
различные объекты при помощи одного или нескольких чисел, а соотношения
между объектами - равенствами, связывающими эти числа или системы
чисел. Некоторые из величин, называемые скалярными (масса, температура и т.
д.), описываются одним числом, причём значение этих величин не изменяется
при переходе от одной системы координат к другой (мы рассматриваем здесь
физические явления с точки зрения классической физики). Другие величины -
векторные (сила, скорость и т. д.), описываются тремя числами (компонентами
вектора), причём при переходе от одной системы координат к другой компоненты
вектора преобразуются по определённому закону. Наряду со скалярными и
векторными величинами встречаются во многих вопросах физики и геометрии
величины более сложного строения. Эти величины, называемые тензорными,
описываются в каждой системе координат несколькими числами (компонентами
тензора), причём закон преобразования этих чисел при переходе от одной
системы
координат к другой более
сложен, чем для векторов (точные определения будут даны ниже). При введении
координатной системы, помимо чисел, описывающих сам объект или физическое
явление, появляются числа, описывающие его связь с выбранной системой
координат. Рассмотрим, например, совокупность чисел
Jij (i,
j = 1, 2, 3),
где
Jij-
осевой момент инерции твёрдого тела относительно оси Xi, a
Jij,
(при i ¹j) - центробежные
моменты инерции, взятые с обратным знаком.
При переходе от одной
системы координат к другой осевой момент инерции Jii меняется (так
как меняется положение оси xi относительно тела), а потому Jii
не может рассматриваться как физическая величина, имеющая независимый
от выбора системы координат смысл. Это находит своё выражение, например, в
том, что знание Jii в одной системе координат не позволяет найти
Jii в другой системе координат. В то же время совокупность всех
чисел Jij имеет смысл, независимый от
выбора координатной системы. Знание всех чисел Jij в одной
системе прямоугольных координат позволяет найти
их в любой другой системе прямоугольных координат по формуле
рис.
5
Попытайтесь осознать, как по образу и подобию вращение базисного спинорного
кубика трансформируется в иные "кубики", каждый из которых обладает собственным
"очарованием","красотой" и другими мистическими свойствами, которыми физики
щедро награждают, например, свойства кварков.
Даннаяя спинорная матрица является
матрицей, размерностью 9х9, т.е. она имеет в своем составе 9х9=81 спинорных
чисел.
Если из этой матрицы вычленить 17
чисел, стоящих на главных диагоналях и представляющих собой "нормированные
спиноры", то мы получим 81-17=64 спинорных числа.
В матрице, размерностью 7х7 таких
перенормировочных спиноров будет
13. В матрице 5х5 таких
перенормированных спиноров будет 9,
а матрица размерностью 3х3 является уже базисной спинорной матрицей, формирующей
все собственное пространство спинорной матрицы.
Из анализа свойств
чисел спинорной матрицы следует, что числа, стоящи на главных диагоналях
спинорной матрицы, определяют число ее взаимодополнительных Великих
Пределов.
Важнейшее
свойство спинорной матрицы (рис. 3) заключается в том, что любое спинорное число
этой матрицы может порождать, по образу и подобию, собственную спинорную
матрицу.
Перенормировка спиноров приводит к тому, что они периодически становятся
инвариантными сами себе и начинают отличаться друг от друга только "цветом",
несущим в себе "допплеровское смещение" базисной ориентации спинора. Полагаю,
что уникальные свойства чисел этой матрицы привлекут к себе внимание
ученых многих направлений.
2.
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
2.1.
ОСНОВЫ ТЕОРИИ
[БСЭ:
Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9
изд., М., 1965;
Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд.,
М., 1967; Схоутен Я. А.,
Тензорный анализ для физиков, пер. с англ., М., 1965;
Мак-Коннел А.-Д.,
Введение в тензорный анализ, пер. с англ., М., 1963;
Сокольников И. О.,
Тензорный анализ, пер. с англ., М., 1971.]
Историческая справка.
Возникновение тензорного исчисления было подготовлено
в 19 веке развитием теории алгебраических форм, с
одной стороны, и теории квадратичных дифференциальных форм -
с другой. Исследования в области теории дифференциальных квадратичных форм
были непосредственно связаны с дифференциальной геометрией: с геометрией
поверхностей (К. Гаусс) и с геометрией многомерного
метрического пространства (Б. Риман). Современную форму
тензорному исчислению придал итальянский математик Г. Риччи-Курбастро,
поэтому тензорнон исчисление иногда называется
исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого
распространения. Внимание к ним возросло после появления (1915-16)
общей теории относительности А. Эйнштейна, математическая часть которой
целиком основана на тензорном исчислении.
Тензор
(от лат. tensus -
напряжённый, натянутый), математический термин, появившийся в середине 19 века
и с тех пор применяющийся в двух различных смыслах. Наибольшее
распространение термин «тензор» получил в современном
тензорном исчислении,
где это название присваивается особого рода величинам, преобразующимся по
особому закону. В механике, особенно в теории упругости, термин «тензор»
широко применяется как синоним симметрического аффинора, то есть линейного
оператора Ф, преобразующего вектор х в вектор
Фх, и симметрического в том смысле, что
скалярное произведение уФх
не меняется при перестановке векторов х и у. Здесь термин был первоначально
связан с малыми растяжениями (и сжатиями), возникающими при упругой
деформации (откуда и название «тензор»),
а затем перенесён в другие области механики. Так появились
тензор
деформации,
тензор
напряжения,
тензор
инерции и др.
Тензорное
исчисление,
математическая теория, изучающая величины особого рода - тензоры, их
свойства и правила действий над ними.
Тензорное исчисление
является развитием и обобщением векторного исчисления и теории матриц.
Тензорное
исчисление
широко применяется в дифференциальной геометрии, теории римановых
пространств, теории относительности, механике, электродинамике и других
областях науки. Для описания многих физических и геометрических фактов
обычно вводится та или иная система координат, что позволяет описывать
различные объекты при помощи одного или нескольких чисел, а соотношения
между объектами - равенствами, связывающими эти числа или системы
чисел. Некоторые из величин, называемые скалярными (масса, температура и т.
д.), описываются одним числом, причём значение этих величин не изменяется
при переходе от одной системы координат к другой (мы рассматриваем здесь
физические явления с точки зрения классической физики). Другие величины -
векторные (сила, скорость и т. д.), описываются тремя числами (компонентами
вектора), причём при переходе от одной системы координат к другой компоненты
вектора преобразуются по определённому закону. Наряду со скалярными и
векторными величинами встречаются во многих вопросах физики и геометрии
величины более сложного строения. Эти величины, называемые тензорными,
описываются в каждой системе координат несколькими числами (компонентами
тензора), причём закон преобразования этих чисел при переходе от одной
системы
координат к другой более
сложен, чем для векторов (точные определения будут даны ниже). При введении
координатной системы, помимо чисел, описывающих сам объект или физическое
явление, появляются числа, описывающие его связь с выбранной системой
координат. Рассмотрим, например, совокупность чисел
Jij (i,
j = 1, 2, 3),
где
Jij-
осевой момент инерции твёрдого тела относительно оси Xi, a
Jij,
(при i ¹j) - центробежные
моменты инерции, взятые с обратным знаком.
При переходе от одной
системы координат к другой осевой момент инерции Jii меняется (так
как меняется положение оси xi относительно тела), а потому Jii
не может рассматриваться как физическая величина, имеющая независимый
от выбора системы координат смысл. Это находит своё выражение, например, в
том, что знание Jii в одной системе координат не позволяет найти
Jii в другой системе координат. В то же время совокупность всех
чисел Jij имеет смысл, независимый от
выбора координатной системы. Знание всех чисел Jij в одной
системе прямоугольных координат позволяет найти
их в любой другой системе прямоугольных координат по формуле
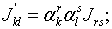 (
(
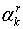 и и  - некоторые числа): здесь, как принято в
тензорном
исчислении
, опущен знак суммы и считается, что если один и тот же
индекс встречается дважды (один раз наверху, а другой раз внизу), то
по нему производится суммирование,
причём этот индекс принимает все возможные для него значения (в
приведённом примере - значения 1, 2, 3).
Тензорное
исчисление , как
и векторное исчисление, является математическим аппаратом, при котором
исключается влияние выбора координатной системы. Это достигается тем,
что задание компонент тензора в какой-либо системе координат определяет их
во всех других системах координат. В тензорном исчислении
указываются методы получения соотношений между тензорами и функций от
компонент тензоров, не меняющихся при переходе от одной системы координат к
другой (инвариантных соотношений и инвариантов). Таким
образом, одной из основных задач
тензорного
исчисления
является нахождение аналитических формулировок законов механики, геометрии,
физики, не
зависящих от выбора координатной системы.
Тензоры в
прямоугольных координатах.
Величины, которые в каждой системе прямоугольных координат задаются в
3-мерном пространстве 3k числами
- некоторые числа): здесь, как принято в
тензорном
исчислении
, опущен знак суммы и считается, что если один и тот же
индекс встречается дважды (один раз наверху, а другой раз внизу), то
по нему производится суммирование,
причём этот индекс принимает все возможные для него значения (в
приведённом примере - значения 1, 2, 3).
Тензорное
исчисление , как
и векторное исчисление, является математическим аппаратом, при котором
исключается влияние выбора координатной системы. Это достигается тем,
что задание компонент тензора в какой-либо системе координат определяет их
во всех других системах координат. В тензорном исчислении
указываются методы получения соотношений между тензорами и функций от
компонент тензоров, не меняющихся при переходе от одной системы координат к
другой (инвариантных соотношений и инвариантов). Таким
образом, одной из основных задач
тензорного
исчисления
является нахождение аналитических формулировок законов механики, геометрии,
физики, не
зависящих от выбора координатной системы.
Тензоры в
прямоугольных координатах.
Величины, которые в каждой системе прямоугольных координат задаются в
3-мерном пространстве 3k числами  (ir = 1, 2, 3) и при замене системы координат
(ir = 1, 2, 3) и при замене системы координат
 системой системой
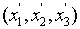 заменяются числами заменяются числами
 по формулам: по формулам:
 (*)
где
(*)
где
 , называются тензорными величинами, а
определяющие их системы чисел - тензорами в
прямоугольных координатах (иногда тензорами называют также и сами тензорные
величины). Число k называется валентностью (рангом)
тензора, числа — его компонентам и (координатами). Аналогичным образом
определяются тензоры в пространстве любого числа измерений.
Примеры тензоров: если координаты вектора а обозначить ai
(i = 1, 2, 3), то числа а, образуют тензор первой валентности.
Любым
двум векторам а = {ai} и b ={bi} соответствует тензор
с компонентами pij = ai* bj.
Этот тензор называется диадой.
Если a (x1,
x2, x3) - некоторое векторное
поле, то каждой точке этого поля соответствует тензор с компонентами , называются тензорными величинами, а
определяющие их системы чисел - тензорами в
прямоугольных координатах (иногда тензорами называют также и сами тензорные
величины). Число k называется валентностью (рангом)
тензора, числа — его компонентам и (координатами). Аналогичным образом
определяются тензоры в пространстве любого числа измерений.
Примеры тензоров: если координаты вектора а обозначить ai
(i = 1, 2, 3), то числа а, образуют тензор первой валентности.
Любым
двум векторам а = {ai} и b ={bi} соответствует тензор
с компонентами pij = ai* bj.
Этот тензор называется диадой.
Если a (x1,
x2, x3) - некоторое векторное
поле, то каждой точке этого поля соответствует тензор с компонентами
 .
Он называется производной
вектора а = {ai} по вектору r {x1, x2, x3}
(обозначается также через .
Он называется производной
вектора а = {ai} по вектору r {x1, x2, x3}
(обозначается также через ). Упомянутая выше совокупность чисел Jij образует тензор второй
валентности (тензор инерции).
2.
Тензоры второй
валентности. В
приложениях Т. и. к механике, кроме тензоров первой валентности
векторов), чаще всего встречаются тензоры второй валентности.
Если pij = pji,
то тензор называется симметрическим, а если pij = –pji,
то - кососимметрическим (антисимметрическим).
Симметрический тензор имеет шесть существенных компонент, а
кососимметрический - три:
). Упомянутая выше совокупность чисел Jij образует тензор второй
валентности (тензор инерции).
2.
Тензоры второй
валентности. В
приложениях Т. и. к механике, кроме тензоров первой валентности
векторов), чаще всего встречаются тензоры второй валентности.
Если pij = pji,
то тензор называется симметрическим, а если pij = –pji,
то - кососимметрическим (антисимметрическим).
Симметрический тензор имеет шесть существенных компонент, а
кососимметрический - три:
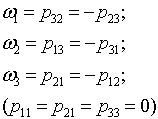 При этом компоненты
При этом компоненты
 преобразуются
как компоненты псевдовектора. Вообще псевдовекторы (угловую скорость,
векторное произведение двух векторов и др.) можно рассматривать как
кососимметрические тензоры второй валентности.
Русская матрица (Русская
матрица) представляет собой кососимметрическую
матрицу в которой три оси симметрии связаны соотношениями преобразуются
как компоненты псевдовектора. Вообще псевдовекторы (угловую скорость,
векторное произведение двух векторов и др.) можно рассматривать как
кососимметрические тензоры второй валентности.
Русская матрица (Русская
матрица) представляет собой кососимметрическую
матрицу в которой три оси симметрии связаны соотношениями

|
В
|
Ф-4
|
Ф-3
|
Ф-2
|
Ф-1
|
Ф0
|
Ф1
|
Ф2
|
Ф3
|
Ф4
|
A*
|
| |
256
|
128
|
64
|
32
|
16
|
8
|
4
|
2
|
1
|
|
| |
128
|
64
|
32
|
16
|
8
|
4
|
2
|
1
|
1/2
|
|
| |
64
|
32
|
16
|
8
|
4
|
2
|
1
|
1/2
|
1/4
|
|
| |
32
|
16
|
8
|
4
|
2
|
1
|
1/2
|
1/4
|
1/8
|
|
|
С
|
16
|
8
|
4
|
2
|
1
|
1/2
|
1/4
|
1/8
|
1/16
|
С*
|
| |
8
|
4
|
2
|
1
|
1/2
|
1/4
|
1/8
|
1/16
|
1/32
|
|
| |
4
|
2
|
1
|
1/2
|
1/4
|
1/8
|
1/16
|
1/32
|
1/64
|
|
| |
2
|
1
|
1/2
|
1/4
|
1/8
|
1/16
|
1/32
|
1/64
|
1/128
|
|
| |
1
|
1/2
|
1/4
|
1/8
|
1/16
|
1/32
|
1/64
|
1/128
|
1/256
|
|
|
A
|
Ф-4
|
Ф-3
|
Ф-2
|
Ф-1
|
Ф0
|
Ф1
|
Ф2
|
Ф3
|
Ф4
|
В*
|
рис.
6
Такие матрицы будем называют бисимметрическими.
Основу Русской матрицы составляет бинарный степенной ряд
.... +25+24+23+22+21+20+2-1+2-2+2-3+2-4+2-5+.....
Из
этого ряда сплетены строки и столбцы Русской матрицы, которые затем
умножаются на золотой ряд
... ,Ф-4,Ф-3,Ф-2,Ф-1,Ф0,Ф1,Ф2,Ф3,Ф4,...
где
Ф1=1, 618....
Если теперь вместо чисел в бисимметрическую матрицу подставить значения показателей степеней
бинарного ряда, что равносильно операции логарифмирования, то мы получим кососимметрическую матрицу, в которой
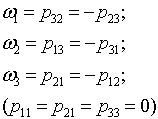 Далее, если в любой системе координат принять
Далее, если в любой системе координат принять
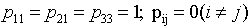 ,
то получится тензор, называемый единичным тензором. Компоненты этого тензора
обозначаются при помощи Кронекера символа ,
то получится тензор, называемый единичным тензором. Компоненты этого тензора
обозначаются при помощи Кронекера символа
 .
Тензоры
инерции, напряжения, единичный тензор -
симметрические. Всякий тензор единственным образом разлагается на сумму
симметрических и кососимметрических тензоров. Если а (r) -
вектор смещения частиц упругого тела при малой деформации, то симметрическая
часть .
Тензоры
инерции, напряжения, единичный тензор -
симметрические. Всякий тензор единственным образом разлагается на сумму
симметрических и кососимметрических тензоров. Если а (r) -
вектор смещения частиц упругого тела при малой деформации, то симметрическая
часть  называется тензором
деформации; кососимметрическая часть
называется тензором
деформации; кососимметрическая часть  соответствует
псевдовектору соответствует
псевдовектору  .
Тензор является симметрическим только в том случае, когда поле а (r)
потенциально. Разложение тензора .
Тензор является симметрическим только в том случае, когда поле а (r)
потенциально. Разложение тензора
 на
симметрические и кососимметрические части соответствует разложению
относительного смещения
da
на чистую деформацию и на поворот тела как целого.
Инвариантами тензора называются функции от его компонент, не
зависящие от выбора координатной системы. Примером инварианта является след
тензора p11 + p22 + p33. Так, для тензора
инерции он равен
удвоенному
полярному моменту инерции относительно начала координат, для тензора на
симметрические и кососимметрические части соответствует разложению
относительного смещения
da
на чистую деформацию и на поворот тела как целого.
Инвариантами тензора называются функции от его компонент, не
зависящие от выбора координатной системы. Примером инварианта является след
тензора p11 + p22 + p33. Так, для тензора
инерции он равен
удвоенному
полярному моменту инерции относительно начала координат, для тензора  - дивергенции векторного поля a (r) и т. д.
Возвращаясь к анализу свойств кососиметрических тензоров и
их разновидности -бисимметрических тензоров, нетрудно увидеть, что их
существенные компоненты
- дивергенции векторного поля a (r) и т. д.
Возвращаясь к анализу свойств кососиметрических тензоров и
их разновидности -бисимметрических тензоров, нетрудно увидеть, что их
существенные компоненты
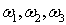 являются
взаимодополнительными и отражают янский или иньский аспекты целостной
монады, т.е. их взаимоотношения определяются рыночными отношениями монады
(рис. 1).
Существенные компоненты кососимметрических и бисимметрических тензоров тесно
взаимоувязаны между собой во вращающемся кресте законов сохранения (Законы
сохранения). являются
взаимодополнительными и отражают янский или иньский аспекты целостной
монады, т.е. их взаимоотношения определяются рыночными отношениями монады
(рис. 1).
Существенные компоненты кососимметрических и бисимметрических тензоров тесно
взаимоувязаны между собой во вращающемся кресте законов сохранения (Законы
сохранения).
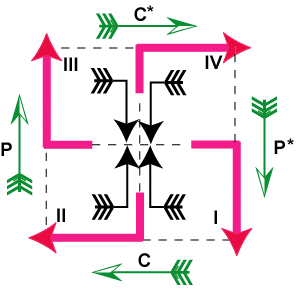 рис.
7
Закон сохранения зеркальной симметрии (С-инвариантность) отражает
инвариантные преобразования кососиммерических тензоров, когда "правое"
заменяется на "левое", а "левое" становится "правым". Закон зарядовой
симметрии (Р-инвариантность) отражает инвариантные преобразования, когда
"внешнее" становится "внутренним", в "внутреннее" становится "внешним".
Нетрудно осознать, что эти законы сохранения проявляются и в свойствах
тензоров. Кососимметрические тензоры характеризуют зеркальные инвариантные
преобразования. Бисимметрические тензоры - отражают свойства симметрии
зарядовых преобразований.
Действия над
тензорами.
Существуют четыре основные операции над тензорами:
сложение тензоров,
умножение тензоров, свёртывание тензоров по двум или более индексам и
перестановка индексов тензора. Так как тензор задаётся своими компонентами в
различных системах координат, то действия над тензорами задаются формулами,
выражающими в каждой системе координат компоненты результата действия через
компоненты тензоров, над которыми производятся действия. При этом формулы
должны быть такими, чтобы в
результате выполнения действия получился тензор.
а)
Сложение тензоров.
Суммой двух тензоров
рис.
7
Закон сохранения зеркальной симметрии (С-инвариантность) отражает
инвариантные преобразования кососиммерических тензоров, когда "правое"
заменяется на "левое", а "левое" становится "правым". Закон зарядовой
симметрии (Р-инвариантность) отражает инвариантные преобразования, когда
"внешнее" становится "внутренним", в "внутреннее" становится "внешним".
Нетрудно осознать, что эти законы сохранения проявляются и в свойствах
тензоров. Кососимметрические тензоры характеризуют зеркальные инвариантные
преобразования. Бисимметрические тензоры - отражают свойства симметрии
зарядовых преобразований.
Действия над
тензорами.
Существуют четыре основные операции над тензорами:
сложение тензоров,
умножение тензоров, свёртывание тензоров по двум или более индексам и
перестановка индексов тензора. Так как тензор задаётся своими компонентами в
различных системах координат, то действия над тензорами задаются формулами,
выражающими в каждой системе координат компоненты результата действия через
компоненты тензоров, над которыми производятся действия. При этом формулы
должны быть такими, чтобы в
результате выполнения действия получился тензор.
а)
Сложение тензоров.
Суммой двух тензоров  и
и 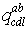 одинакового строения (то
есть имеющих одинаковое число верхних и нижних индексов) называется тензор с
компонентами одинакового строения (то
есть имеющих одинаковое число верхних и нижних индексов) называется тензор с
компонентами
 б)
Умножение тензоров.
Произведением двух тензоров
б)
Умножение тензоров.
Произведением двух тензоров  и
и 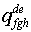 (быть может различного
строения) называется тензор с компонентами (быть может различного
строения) называется тензор с компонентами
 Произведение тензоров,
вообще говоря, зависит от порядка сомножителей. Если один из тензоров имеет
нулевую валентность (то есть является скалярной величиной
Произведение тензоров,
вообще говоря, зависит от порядка сомножителей. Если один из тензоров имеет
нулевую валентность (то есть является скалярной величиной
 ), то умножение его на другой тензор
сводится к умножению всех компонент тензора на число ), то умножение его на другой тензор
сводится к умножению всех компонент тензора на число
 .
в)
Свёртывание тензора.
Результатом свёртывания тензора .
в)
Свёртывание тензора.
Результатом свёртывания тензора  по
индексам а и d (верхнему и нижнему) называется тензор по
индексам а и d (верхнему и нижнему) называется тензор
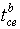 , компоненты которого равны , компоненты которого равны
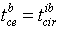 . (здесь производится суммирование по
индексу i). Например, след матрицы . (здесь производится суммирование по
индексу i). Например, след матрицы  является результатом свёртывания её по индексам i и j, бискалярное
произведение
является результатом свёртывания её по индексам i и j, бискалярное
произведение 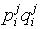 тензоров
тензоров
 и и
 равно результату
свёртывания их произведения по всем индексам. При полном свёртывании тензора
(по всем индексам) получается инвариант.
г)
Перестановка индексов.
Пусть компоненты тензора равно результату
свёртывания их произведения по всем индексам. При полном свёртывании тензора
(по всем индексам) получается инвариант.
г)
Перестановка индексов.
Пусть компоненты тензора  выражаются
через компоненты тензора выражаются
через компоненты тензора  формулой
формулой 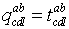 . Тогда говорят, что . Тогда говорят, что  получился из
получился из  перестановкой индексов с
и е. При этом переставляться могут только индексы одного и того же уровня.
Тензорный анализ.
В приложениях приходится обычно рассматривать не отдельные тензоры, а
тензорные поля. Например, при изучении упругой деформации рассматривают
тензоры деформации и напряжений во всех точках тела. Если в пространстве
задана прямоугольная система координат, то тензорное поле перестановкой индексов с
и е. При этом переставляться могут только индексы одного и того же уровня.
Тензорный анализ.
В приложениях приходится обычно рассматривать не отдельные тензоры, а
тензорные поля. Например, при изучении упругой деформации рассматривают
тензоры деформации и напряжений во всех точках тела. Если в пространстве
задана прямоугольная система координат, то тензорное поле
 можно рассматривать как совокупность
функций можно рассматривать как совокупность
функций  ,
заданных в каждой точке ,
заданных в каждой точке  области и
преобразующихся при переходе от одной системы прямоугольных координат к
другой по формулам области и
преобразующихся при переходе от одной системы прямоугольных координат к
другой по формулам
 .
В этом случае частные
производные компонент тензора по координатам .
В этом случае частные
производные компонент тензора по координатам
 образуют
также тензор, валентность которого на единицу выше валентности исходного
тензора. Например, при дифференцировании скалярного поля получается поле
градиента, при дифференцировании поля градиента -
поле симметрического тензора второй валентности:
образуют
также тензор, валентность которого на единицу выше валентности исходного
тензора. Например, при дифференцировании скалярного поля получается поле
градиента, при дифференцировании поля градиента -
поле симметрического тензора второй валентности:
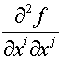 и т. д.
3. ТЕНЗОРНЫЕ
МАТРИЦЫ
Математический аппарат тензорного анализа отражает не только симметрические, но
и асимметрические (кососимметрические и т.п.) взаимоотношения тензоров.
Поэтому мир
тензорных матриц отражает несет в себе и гармонию и дисгармонию мироздания.
Тензоры описывают и равновесность (устойчивость) и неравновесность
взаимоотношений двойственного отношения, порождающего ту, или иную тензорную
матрицу.
На страницах сайта
многие "картинки" несут в себе гармонию симметрии тензорных матриц.
Особенно ярко
гармония взаимоотношений тензоров проявляется в Русской матрице (Русская
матрица), в матрице ДНК (Матрицы ДНК), матрице
пространства-времени (Матрица "
L-T"), матрице Миров и Антимиров (Мир и
Антимир), несущей в себе "разметку" Мироздания, в котором каждому Миру и
Антимиру уже заранее приготовлена соответствующая ниша. И если в результате
возмущения какой-либо мир (антимир) "выпадет" из собственной ниши, то он будет
транспортирован в новую нишу возникающими при этом силами гравитации и
антигравитации.
Выбирая в качестве базисной матрицы двумерную матрицу и применяя к ней
операцию возведения в степень, мы получим следующие матрицы
и т. д.
3. ТЕНЗОРНЫЕ
МАТРИЦЫ
Математический аппарат тензорного анализа отражает не только симметрические, но
и асимметрические (кососимметрические и т.п.) взаимоотношения тензоров.
Поэтому мир
тензорных матриц отражает несет в себе и гармонию и дисгармонию мироздания.
Тензоры описывают и равновесность (устойчивость) и неравновесность
взаимоотношений двойственного отношения, порождающего ту, или иную тензорную
матрицу.
На страницах сайта
многие "картинки" несут в себе гармонию симметрии тензорных матриц.
Особенно ярко
гармония взаимоотношений тензоров проявляется в Русской матрице (Русская
матрица), в матрице ДНК (Матрицы ДНК), матрице
пространства-времени (Матрица "
L-T"), матрице Миров и Антимиров (Мир и
Антимир), несущей в себе "разметку" Мироздания, в котором каждому Миру и
Антимиру уже заранее приготовлена соответствующая ниша. И если в результате
возмущения какой-либо мир (антимир) "выпадет" из собственной ниши, то он будет
транспортирован в новую нишу возникающими при этом силами гравитации и
антигравитации.
Выбирая в качестве базисной матрицы двумерную матрицу и применяя к ней
операцию возведения в степень, мы получим следующие матрицы
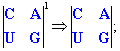
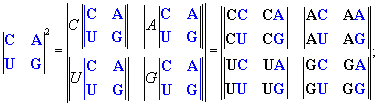
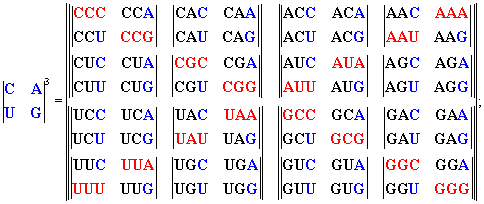 рис.
8
На многих страницах сайта приводились
свойства Русской матрицы. Эта матрица обладает двойственной симметрией (бисимметрическая
матрица).
Рассмотрим возведение в степень
базисной матрицы бинарного степенного ряда
рис.
8
На многих страницах сайта приводились
свойства Русской матрицы. Эта матрица обладает двойственной симметрией (бисимметрическая
матрица).
Рассмотрим возведение в степень
базисной матрицы бинарного степенного ряда
Выполняя возведение в степень, получим
 рис.
9
Результирующая
матрица размерностью 9х9=81 число, обладает уникальными свойствами
симметрии.
Все главные диагонали клеточных
матриц, идущие слева-вверх имеют одно и то же значение, выписывая
которые, мы получим исходную базисную матрицу, т.е. этот феномен
отражает свойства симметрии тензоров высших измерений в проекциях на
тензорные матрицы низших измерений.
А всему виной -единицы, стоящие на главной диагонали базисной матрицы.
Осуществляя из матрицы высшей
симметрии клеточные матрицы, вырезки клеточных матриц размерностью 6х6,
мы можем получить соответствующие проекции тензора высших измерений на
двумерную плоскость-матрицу размерности 2х2.
4. ТЕНЗОРНЫЕ
МАТРИЦЫ ВЫСШИХ ИЗМЕРЕНИЙ
Возведение базисной матрицы в степень, в соответствии с Единым законом
эволюции двойственного отношения, периодически приводит к
перенормировке чисел тензорных матриц.
Для понимания сущности подобных
перенормировок рассмотрим свойства следующей бисимметрической матрицы (Матрицы
ДНК).
рис.
9
Результирующая
матрица размерностью 9х9=81 число, обладает уникальными свойствами
симметрии.
Все главные диагонали клеточных
матриц, идущие слева-вверх имеют одно и то же значение, выписывая
которые, мы получим исходную базисную матрицу, т.е. этот феномен
отражает свойства симметрии тензоров высших измерений в проекциях на
тензорные матрицы низших измерений.
А всему виной -единицы, стоящие на главной диагонали базисной матрицы.
Осуществляя из матрицы высшей
симметрии клеточные матрицы, вырезки клеточных матриц размерностью 6х6,
мы можем получить соответствующие проекции тензора высших измерений на
двумерную плоскость-матрицу размерности 2х2.
4. ТЕНЗОРНЫЕ
МАТРИЦЫ ВЫСШИХ ИЗМЕРЕНИЙ
Возведение базисной матрицы в степень, в соответствии с Единым законом
эволюции двойственного отношения, периодически приводит к
перенормировке чисел тензорных матриц.
Для понимания сущности подобных
перенормировок рассмотрим свойства следующей бисимметрической матрицы (Матрицы
ДНК).
 рис.
10
Эта матрица получена умножением 1-й строки матрицы И-Цзин на
триграммный столбец. В результате умножения мы получаем триграммную
матрицу И-Цзин, каждый триплет которой
состоит из трех триграмм.
А поскольку в 1-й строке матрицы И-Цзин стоит "белая" триграмма,
то она "окрашивает" своим цветом все другие триплеты. При этом три белые
триграммы образуют Великий Предел всей этой матрицы. Это "перенормировочный
триплет". И это свойство проявляется на всех уровнях мироздания. В
частности, при рассмотрении свойств матрицы ДНК, отмечалось, что
начиная
с уровня соответствия множества 64 триплетов
множеству 20 аминокислот
начинает наблюдаться
значительное эволюционное разнообразие кодов,
и в каждом генетическом коде
любая из 20 аминокислот кодируется
определенным числом триплетов. Это число кодирующих триплетов называют числом вырожденности аминокислоты
в данном коде (С.В.Петухов). Разные генетические
коды имеют несколько разные совокупности своих чисел вырожденности для
унифицированного набора из 20 аминокислот.
Множество вариантов
генетических кодов, отличающихся по своей вырожденности, отражает
особенности биологической эволюции на самых базовых уровнях.
Заменяя строку Замысла творения на удвоенные
триграммы, получим следующую матрицу.
рис.
10
Эта матрица получена умножением 1-й строки матрицы И-Цзин на
триграммный столбец. В результате умножения мы получаем триграммную
матрицу И-Цзин, каждый триплет которой
состоит из трех триграмм.
А поскольку в 1-й строке матрицы И-Цзин стоит "белая" триграмма,
то она "окрашивает" своим цветом все другие триплеты. При этом три белые
триграммы образуют Великий Предел всей этой матрицы. Это "перенормировочный
триплет". И это свойство проявляется на всех уровнях мироздания. В
частности, при рассмотрении свойств матрицы ДНК, отмечалось, что
начиная
с уровня соответствия множества 64 триплетов
множеству 20 аминокислот
начинает наблюдаться
значительное эволюционное разнообразие кодов,
и в каждом генетическом коде
любая из 20 аминокислот кодируется
определенным числом триплетов. Это число кодирующих триплетов называют числом вырожденности аминокислоты
в данном коде (С.В.Петухов). Разные генетические
коды имеют несколько разные совокупности своих чисел вырожденности для
унифицированного набора из 20 аминокислот.
Множество вариантов
генетических кодов, отличающихся по своей вырожденности, отражает
особенности биологической эволюции на самых базовых уровнях.
Заменяя строку Замысла творения на удвоенные
триграммы, получим следующую матрицу.
 рис.
11
рис.
11
В этой матрице все триграммы высшего уровня оказываются самодостаточными, а
триграммы, стоящие на главной диагонали - оказываются перенормировочными
триплетами (цветными Великими Пределами).
Более того, поскольку
строка является упорядоченной в соответствии с цветами радуги, то и цветные
Великие пределы также оказываются упорядоченными и формируют триплетную
радугу высшего измерения.
Теперь снова вернемся к спинорному и тензорному
исчислению.
Обозначая условно янский аспект через "+",
а иньский =через "-", умножим базисную матрицу 2х2 саму на себя.
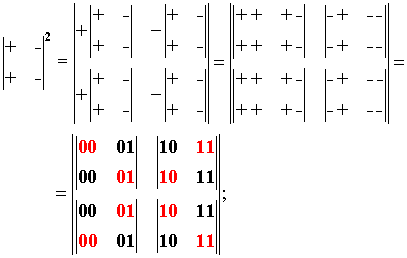 рис. 12
Из рисунка
видно, что на главных диагоналях начинается формироваться натуральный ряд
чисел 0,1,2,3.
если же базисную матрицу
"ян-инь" возвести в третью степень, то мы получим следующую матрицу
рис. 12
Из рисунка
видно, что на главных диагоналях начинается формироваться натуральный ряд
чисел 0,1,2,3.
если же базисную матрицу
"ян-инь" возвести в третью степень, то мы получим следующую матрицу
 рис. 13
Видите, на главной диагонали этой матрицы
сформировались триграммы И-Цзин с двоичным кодом 0,1,2,3,4,5,6,7.
рис. 13
Видите, на главной диагонали этой матрицы
сформировались триграммы И-Цзин с двоичным кодом 0,1,2,3,4,5,6,7.
 рис. 14
Если теперь главную
диагональ умножить саму на себя, то мы получим классическую матрицу И-Цзин
рис. 14
Если теперь главную
диагональ умножить саму на себя, то мы получим классическую матрицу И-Цзин
 рис. 15
Видите, на главной диагонали матрицы стоят
квадраты триграмм.
12:22:32:42:52:...
Мы получили уникальный
результат.
Во-первых, из рис. 10 мы видим, что такой ряд порождает себе подобный ряд
высшего измерения, и приводит к периодическим перенормировкам
триплетов. Самое важное заключается в том, что мы не делаем нигде акцент на
природу этого ряда. Этот означает, что данный механизм
перенормировок работает на всех уровнях иерархии и не зависит от природы
двойственного отношения. Это относится к эволюции любого двойственного
отношения
(пространство-время,
человек-общество, сознание-подсознание, объект-субъект, и т.д.).
Наиболее ярко эта
закономерность проявляется в свойствах Периодической системы химических
элементов (О химических элементах).
Может быть, настала пора ввести в тензорное и спинорное исчисления
соответствующие
операции
(и операторы) перенормировки? Сегодня они
присутствуют там как инструмент математического искусства, которым
можно пользоваться, или не пользоваться.
5.
ЭНЕРГЕТИЧЕСКО-ИНФОРМАЦИОННАЯ РЕЗОНАНСНАЯ МАТРИЦА
На странице
"Творце", "О химических
элементах" и других были рассмотрены свойства следующих клеточных
матриц, отражающих структуру Периодической системы химических элементов
рис. 15
Видите, на главной диагонали матрицы стоят
квадраты триграмм.
12:22:32:42:52:...
Мы получили уникальный
результат.
Во-первых, из рис. 10 мы видим, что такой ряд порождает себе подобный ряд
высшего измерения, и приводит к периодическим перенормировкам
триплетов. Самое важное заключается в том, что мы не делаем нигде акцент на
природу этого ряда. Этот означает, что данный механизм
перенормировок работает на всех уровнях иерархии и не зависит от природы
двойственного отношения. Это относится к эволюции любого двойственного
отношения
(пространство-время,
человек-общество, сознание-подсознание, объект-субъект, и т.д.).
Наиболее ярко эта
закономерность проявляется в свойствах Периодической системы химических
элементов (О химических элементах).
Может быть, настала пора ввести в тензорное и спинорное исчисления
соответствующие
операции
(и операторы) перенормировки? Сегодня они
присутствуют там как инструмент математического искусства, которым
можно пользоваться, или не пользоваться.
5.
ЭНЕРГЕТИЧЕСКО-ИНФОРМАЦИОННАЯ РЕЗОНАНСНАЯ МАТРИЦА
На странице
"Творце", "О химических
элементах" и других были рассмотрены свойства следующих клеточных
матриц, отражающих структуру Периодической системы химических элементов

 рис. 16
Эти клеточные матрицы
были получены в полном соответствии с приведенными выше операциями и
тензорного и спинорного умножения. При этом в каждой клеточной матрице
взаимоотношения между четырьмя компонентами строятся в соответствии с
принципами максимина и минимакса.
рис. 16
Эти клеточные матрицы
были получены в полном соответствии с приведенными выше операциями и
тензорного и спинорного умножения. При этом в каждой клеточной матрице
взаимоотношения между четырьмя компонентами строятся в соответствии с
принципами максимина и минимакса.
 Выполняя формальные
операции тензорного умножения этой матрицы саму на себя, получим
Выполняя формальные
операции тензорного умножения этой матрицы саму на себя, получим
 Это тождество отражает
закон "спроса" и "предложения" атомной оболочки, состоящей
уже из 8 протонов и
восьми электронов.Видите. как последовательно увеличивается
сложность и потенциал электронных и протонных оболочек, включая и потенциалы
отдельных протонов и электронов.
Следовательно,
Периодическая система химических элементов формируется в полном соответствии
с правилами тензорного и спинорного умножения исходной матрицы на саму себя.
6.
ТЕНЗОРНЫЕ МАТРИЦЫ ДНК МИРОЗДАНИЙ
Вот мы и
подходим к финалу, определяя спинорные матрицы ДНК мирозданий.
рассматриваемые выше
тензорные и спинорные матрицы отражают свойства свернутого на
плоскость гиперкуба.
Эти свойства проявляются
в свойствах матрицы И-Цзин, размерностью 8х8.
Это тождество отражает
закон "спроса" и "предложения" атомной оболочки, состоящей
уже из 8 протонов и
восьми электронов.Видите. как последовательно увеличивается
сложность и потенциал электронных и протонных оболочек, включая и потенциалы
отдельных протонов и электронов.
Следовательно,
Периодическая система химических элементов формируется в полном соответствии
с правилами тензорного и спинорного умножения исходной матрицы на саму себя.
6.
ТЕНЗОРНЫЕ МАТРИЦЫ ДНК МИРОЗДАНИЙ
Вот мы и
подходим к финалу, определяя спинорные матрицы ДНК мирозданий.
рассматриваемые выше
тензорные и спинорные матрицы отражают свойства свернутого на
плоскость гиперкуба.
Эти свойства проявляются
в свойствах матрицы И-Цзин, размерностью 8х8.
 Эти свойства
проявляются и в расширенной матрице И-Цзин, размерностью 9х9 (рис. 11).
Но еще древние греки
установили, что все известные людям кристаллы в конечном итоге отражают в
себе свойства Платоновых тел.
Эти свойства
проявляются и в расширенной матрице И-Цзин, размерностью 9х9 (рис. 11).
Но еще древние греки
установили, что все известные людям кристаллы в конечном итоге отражают в
себе свойства Платоновых тел.
 рис. 17
так, из рисунка 17 следует, что свойства
следующих более совершенных мирозданий должны по образу и подобию
проявляться в свойствах гиперикосаэдра и гипердодекаэдра.
рис. 17
так, из рисунка 17 следует, что свойства
следующих более совершенных мирозданий должны по образу и подобию
проявляться в свойствах гиперикосаэдра и гипердодекаэдра.
 рис. 18
Даная матрица имеет размерность уже 12х12 и
содержит в себе 144 вершины, а также Великий предел всего гиперкристалла.
Данную матрицу, отражающую в себе законы симметрии свернутого гиперкристалла
(гиперикосаэдра), по праву следует считать
Зодиакальной.
Эта матрица в свернутом виде отражается в
свойствах матрицы размерности 3х3, т.е. она непосредственно получается из
матрицы куба. в котором каждая вершина состоит из четырех
взаимодополнительных тетраэдров.
Но самой совершенной
матрицей, отражающей в себе свойства гипердодекаэдра следует считать матрицу
ДНК, имеющую размерность 20х20 и содержащую 400 вершин и конечно Великий
предел гипердодекаэдра (Число).
Как здесь не вспомнить концепцию Пифагора
"ВСЕ ЕСТЬ ЧИСЛО".
рис. 18
Даная матрица имеет размерность уже 12х12 и
содержит в себе 144 вершины, а также Великий предел всего гиперкристалла.
Данную матрицу, отражающую в себе законы симметрии свернутого гиперкристалла
(гиперикосаэдра), по праву следует считать
Зодиакальной.
Эта матрица в свернутом виде отражается в
свойствах матрицы размерности 3х3, т.е. она непосредственно получается из
матрицы куба. в котором каждая вершина состоит из четырех
взаимодополнительных тетраэдров.
Но самой совершенной
матрицей, отражающей в себе свойства гипердодекаэдра следует считать матрицу
ДНК, имеющую размерность 20х20 и содержащую 400 вершин и конечно Великий
предел гипердодекаэдра (Число).
Как здесь не вспомнить концепцию Пифагора
"ВСЕ ЕСТЬ ЧИСЛО".
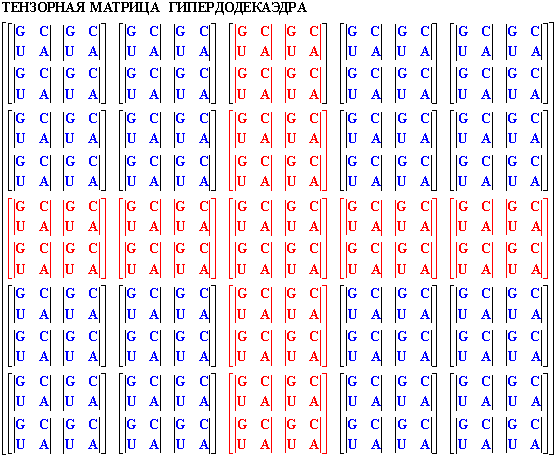 рис. 19
Нетрудно видеть, что данная матрица в свернутом виде является матрицей
размерностью 5х5, но если убрать из нее крест Великих пределов, то мы
получим четыре матрицы И-Цзин.
Огненный крест матрицы
гипердодекаэдра состоит из 9 клеточных матриц, т.е. мы получили
Огненный Куб, каждая вершина которого состоит из
двух звездных тетраэдров.
рис. 19
Нетрудно видеть, что данная матрица в свернутом виде является матрицей
размерностью 5х5, но если убрать из нее крест Великих пределов, то мы
получим четыре матрицы И-Цзин.
Огненный крест матрицы
гипердодекаэдра состоит из 9 клеточных матриц, т.е. мы получили
Огненный Куб, каждая вершина которого состоит из
двух звездных тетраэдров.
 Вот мы и пришли снова к началу мироздания,
но это начало поистине является уже Огненным миром, о свойствах
которого написано множество эзотерической литературы.
Вот мы и пришли снова к началу мироздания,
но это начало поистине является уже Огненным миром, о свойствах
которого написано множество эзотерической литературы.
|

 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©


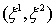

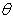







 положив
положив 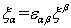 , где
, где  (как всегда, по повторяющимся индексам производится суммирование). Иными
словами,
(как всегда, по повторяющимся индексам производится суммирование). Иными
словами,  .
. .
. 
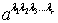



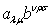 .
.  и
и
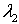 называется спинор
называется спинор









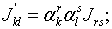
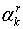

 (ir = 1, 2, 3) и при замене системы координат
(ir = 1, 2, 3) и при замене системы координат
 системой
системой
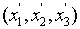 заменяются числами
заменяются числами


 , называются тензорными величинами, а
определяющие их системы чисел
, называются тензорными величинами, а
определяющие их системы чисел  .
.

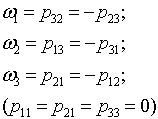


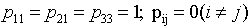

 соответствует
псевдовектору
соответствует
псевдовектору .
.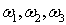 являются
взаимодополнительными и отражают янский или иньский аспекты целостной
монады, т.е. их взаимоотношения определяются рыночными отношениями монады
(рис. 1).
являются
взаимодополнительными и отражают янский или иньский аспекты целостной
монады, т.е. их взаимоотношения определяются рыночными отношениями монады
(рис. 1). 

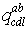 одинакового строения (то
есть имеющих одинаковое число верхних и нижних индексов) называется тензор с
компонентами
одинакового строения (то
есть имеющих одинаковое число верхних и нижних индексов) называется тензор с
компонентами

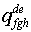 (быть может различного
строения) называется тензор с компонентами
(быть может различного
строения) называется тензор с компонентами 
 ), то умножение его на другой тензор
сводится к умножению всех компонент тензора на число
), то умножение его на другой тензор
сводится к умножению всех компонент тензора на число
 по
индексам а и d (верхнему и нижнему) называется тензор
по
индексам а и d (верхнему и нижнему) называется тензор
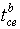 , компоненты которого равны
, компоненты которого равны
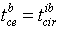 . (здесь производится суммирование по
индексу i). Например, след матрицы
. (здесь производится суммирование по
индексу i). Например, след матрицы  является результатом свёртывания её по индексам i и j, бискалярное
произведение
является результатом свёртывания её по индексам i и j, бискалярное
произведение 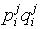


 выражаются
через компоненты тензора
выражаются
через компоненты тензора 
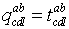 . Тогда говорят, что
. Тогда говорят, что  можно рассматривать как совокупность
функций
можно рассматривать как совокупность
функций
 области и
преобразующихся при переходе от одной системы прямоугольных координат к
другой по формулам
области и
преобразующихся при переходе от одной системы прямоугольных координат к
другой по формулам 
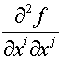 и т. д.
и т. д.