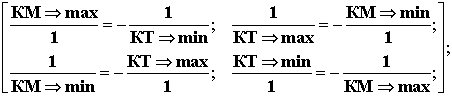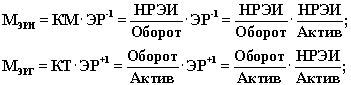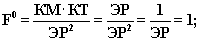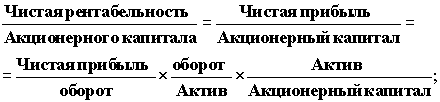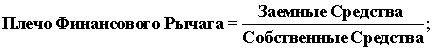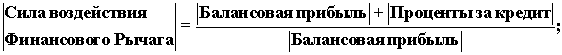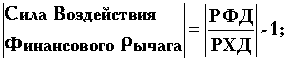ФИНАНСОВЫЙ МЕНЕДЖМЕНТ
ИЛИ
ФИНАНСОВАЯ
МЕХАНИКА
1.
ЭКОНОМИЧЕСКАЯ МЕХАНИКА ИЛИ
ЛОГИКА ФИНАНСОВОГО
МЕХАНИЗМА ПРЕДПРИЯТИЯ
Данная страница не является пособием по финансовому менеджменту, но
публикуемая здесь информация может оказаться полезной и для специалистов в
сфере финансового менеджмента, ибо здесь делается попытка отразить логику
финансового механизма предприятия с позиций Единого Закона.
Используемая терминология и основные положения методики, отражающей логику
финансового механизма предприятий изложены в книге Е.Стояновой
"Финансовый менеджмент", М. Перспектива, 1994 г. Эта книга представляет
самостоятельный интерес для тех, кто хочет более глубоко изучить методику
финансового анализа финансово-хозяйственной деятельности предприятий.
Наша цель лежит в несколько иной плоскости- обосновать всеобщий характер
проявления свойств Единого закона в финансовом менеджменте. Поэтому данная
статья может представить интерес, в первую очередь, для специалистов в
сфере финансово-хозяйственной деятельности, к которым и следует перенаправить
вопрос о том, а можно ли ЭТО использовать на практике.
1.1.
ЭКОНОМИЧЕСКАЯ
РЕНТАБЕЛЬНОСТЬ
Актив-это
затраты и вложения, отражаемые в активе баланса предприятия.
НРЭИ
(Нетто-Результат Эксплуатации Инвестиций)-
отражает прибыль предприятия до уплаты процентов за кредит и уплаты налогов,
т.е. это балансовая прибыль +проценты за кредит.
Теперь можно дать
определить экономическую рентабельность (ЭР)
активов
 В экономической литературе это отношение обычно выражается в процентах. Однако
мы будем использовать относительные единицы. Здесь и ниже под экономической
рентабельностью мы будем понимать экономическая рентабельность активов.
Следовательно относительная экономическая рентабельность активов отражает
долю НРЭИ от Активов. Это дает нам в руки общий инструмент, позволяющий
выражать экономическую рентабельность и относительно других экономических
монад (двойственных отношений).
Развернем
теперь полученное отношение
В экономической литературе это отношение обычно выражается в процентах. Однако
мы будем использовать относительные единицы. Здесь и ниже под экономической
рентабельностью мы будем понимать экономическая рентабельность активов.
Следовательно относительная экономическая рентабельность активов отражает
долю НРЭИ от Активов. Это дает нам в руки общий инструмент, позволяющий
выражать экономическую рентабельность и относительно других экономических
монад (двойственных отношений).
Развернем
теперь полученное отношение
 Здесь
КМ- Коммерческая Маржа,
отражающая результат эксплуатации инвестиций.
По существу это рентабельность
оборота или рентабельность продаж.
КТ-
коэффициент трансформации, показывает, сколько рублей с оборота
снимается с
каждого рубля актива,
т.е. в какой оборот трансформируется
каждый рубль актива. КТ также можно
воспринимать
как оборачиваемость активов. В такой трактовке КТ показывает,
сколько раз
за данный период
оборачивается каждый рубль актива.
Хочу
обратить внимание читателей на мистику развертывания монады ЭР.
Здесь
КМ- Коммерческая Маржа,
отражающая результат эксплуатации инвестиций.
По существу это рентабельность
оборота или рентабельность продаж.
КТ-
коэффициент трансформации, показывает, сколько рублей с оборота
снимается с
каждого рубля актива,
т.е. в какой оборот трансформируется
каждый рубль актива. КТ также можно
воспринимать
как оборачиваемость активов. В такой трактовке КТ показывает,
сколько раз
за данный период
оборачивается каждый рубль актива.
Хочу
обратить внимание читателей на мистику развертывания монады ЭР.
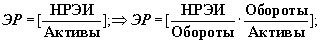 Если положить ЭР=1, то мы получим следующие тождества
Если положить ЭР=1, то мы получим следующие тождества
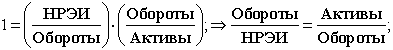 ,
из которых видно, что при неизменных ЭР, и единичных Оборотах, между НРЭИ
и Активами существует обратная зависимость.
Из полученного тождества можно осознать, что неизменная, единичная экономическая
рентабельность несет смысл закона экономического тяготения, порождая
единичную Силу рентабельности активов ,
из которых видно, что при неизменных ЭР, и единичных Оборотах, между НРЭИ
и Активами существует обратная зависимость.
Из полученного тождества можно осознать, что неизменная, единичная экономическая
рентабельность несет смысл закона экономического тяготения, порождая
единичную Силу рентабельности активов
 Здесь
V-скорость
одного оборота, n-число оборотов за один цикл, Mk-масса
капитала (капитал-собственность+ капитал-функция).
Ниже эта Единичная сила рентабельности активов будет определена через
монаду "КМ-КТ".
1.2. ВЕСЫ ЭКОНОМИЧЕСКОЙ
РЕНТАБЕЛЬНОСТИ
В книге Е.Стояновой "Финансовый менеджмент" [],
приводится следующий рисунок
Здесь
V-скорость
одного оборота, n-число оборотов за один цикл, Mk-масса
капитала (капитал-собственность+ капитал-функция).
Ниже эта Единичная сила рентабельности активов будет определена через
монаду "КМ-КТ".
1.2. ВЕСЫ ЭКОНОМИЧЕСКОЙ
РЕНТАБЕЛЬНОСТИ
В книге Е.Стояновой "Финансовый менеджмент" [],
приводится следующий рисунок
 рис. 1
Из этого рисунка
видно, что при фиксированной ЭР с увеличением КТ
происходит уменьшение КМ , т.е имеет место тождество, которое
справедливо только в одном единственном случае, когда между КМ и КТ существует
баланс. Этот баланс, в соответствии с принципом
саморегулирования, можно отразить в форме следующих тождеств
рис. 1
Из этого рисунка
видно, что при фиксированной ЭР с увеличением КТ
происходит уменьшение КМ , т.е имеет место тождество, которое
справедливо только в одном единственном случае, когда между КМ и КТ существует
баланс. Этот баланс, в соответствии с принципом
саморегулирования, можно отразить в форме следующих тождеств
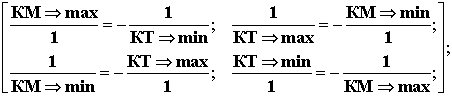 В этих отношениях ЭР
присутствует в неявном виде, ибо она нормирована (приведена к Единице).
Это
матричное тождество отражает все возможные формы взаимоотношений между КМ и КТ
при неизменной экономической рентабельности.
При этом взаимоотношения между членами данной матрицы, стоящих в одной и той же
строке соответствует закону сохранения зеркальной симметрии (а=
- в), а отношения в столбцах матрицы - закону
сохранения зарядовой симметрии (а=1/в).
Соответственно, взаимоотношения между членами матрицы по диагоналям
соответствуют комбинированному закону сохранения симметрии (а=-1/в).
Следовательно, каждый член данной матрицы является одной из алгебраических
форм записи кривой, изображенной на рис. 1.
Матрица уже изначально несет в себе гораздо
большую информацию об экономической рентабельности, чем рис. 1. При этом,
поскольку каждый член матрицы является тождеством, то в итоге мы непосредственно
получаем Куб закона взаимоотношений КМ и КТ, при которых экономическая
рентабельность будет оставаться неизменной.
Это чрезвычайно важный вывод, который
экономистам еще предстоит осмыслить.
Здесь экономическая рентабельность приведена к
Единице,
которая порождает единичное плечо рычага двойственного отношения (рычажных весов
"КМ-КТ").
Действительно, из выражения
для ЭР, приведенных выше следует
В этих отношениях ЭР
присутствует в неявном виде, ибо она нормирована (приведена к Единице).
Это
матричное тождество отражает все возможные формы взаимоотношений между КМ и КТ
при неизменной экономической рентабельности.
При этом взаимоотношения между членами данной матрицы, стоящих в одной и той же
строке соответствует закону сохранения зеркальной симметрии (а=
- в), а отношения в столбцах матрицы - закону
сохранения зарядовой симметрии (а=1/в).
Соответственно, взаимоотношения между членами матрицы по диагоналям
соответствуют комбинированному закону сохранения симметрии (а=-1/в).
Следовательно, каждый член данной матрицы является одной из алгебраических
форм записи кривой, изображенной на рис. 1.
Матрица уже изначально несет в себе гораздо
большую информацию об экономической рентабельности, чем рис. 1. При этом,
поскольку каждый член матрицы является тождеством, то в итоге мы непосредственно
получаем Куб закона взаимоотношений КМ и КТ, при которых экономическая
рентабельность будет оставаться неизменной.
Это чрезвычайно важный вывод, который
экономистам еще предстоит осмыслить.
Здесь экономическая рентабельность приведена к
Единице,
которая порождает единичное плечо рычага двойственного отношения (рычажных весов
"КМ-КТ").
Действительно, из выражения
для ЭР, приведенных выше следует
 Откуда, используя
предыдущие тождества, непосредственно получаем
Откуда, используя
предыдущие тождества, непосредственно получаем
 Вот мы и получили весы, отражающие рыночные отношения между ЭР, КМ и КТ.
Обратите внимание:
в экономической литературе значение ЭР обычно
выражается в процентах. Поэтому единичная диагональ фактически отражает эволюцию
монады "КМ-КТ". Проценты несут информацию об изменении плеча рычагов весов.
Естественно, что каждый процент ЭР переводит монаду "КМКТ" в новое состояние.
Экономическая рентабельност активов (ЭР) здесь служит Великим пределом монады КМ-КТ.
Обратите внимание -левая и правая часть весов отражают комбинированный закон
сохранения симметрии (зеркальная +зарядовая).
Вот мы и получили весы, отражающие рыночные отношения между ЭР, КМ и КТ.
Обратите внимание:
в экономической литературе значение ЭР обычно
выражается в процентах. Поэтому единичная диагональ фактически отражает эволюцию
монады "КМ-КТ". Проценты несут информацию об изменении плеча рычагов весов.
Естественно, что каждый процент ЭР переводит монаду "КМКТ" в новое состояние.
Экономическая рентабельност активов (ЭР) здесь служит Великим пределом монады КМ-КТ.
Обратите внимание -левая и правая часть весов отражают комбинированный закон
сохранения симметрии (зеркальная +зарядовая).
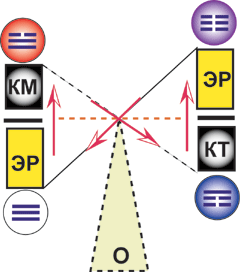 рис. 2
ЭР является истоком и
стоком КМ и КТ. Это точка бифуркации рентабельности. И
она же является точкой синтеза рентабельности.
1.3. МЕХАНИКА РЕНТАБЕЛЬНОСТИ
АКТИВОВ
1.3.1. МАССА РЕНТАБЕЛЬНОСТИ
Перепишем тождество в следующем виде
рис. 2
ЭР является истоком и
стоком КМ и КТ. Это точка бифуркации рентабельности. И
она же является точкой синтеза рентабельности.
1.3. МЕХАНИКА РЕНТАБЕЛЬНОСТИ
АКТИВОВ
1.3.1. МАССА РЕНТАБЕЛЬНОСТИ
Перепишем тождество в следующем виде
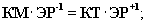 Связывая КМ
с инерционной массой рентабельности активов,
а с КТ - с гравитационной массой, мы получим
Связывая КМ
с инерционной массой рентабельности активов,
а с КТ - с гравитационной массой, мы получим
 или, расписывая, окончательно получим
или, расписывая, окончательно получим
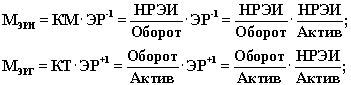 Такая
интерпретация полученных выражений принята потому, что по форме они
напоминают известные из механики Ньютона категории - массы и веса:
m=P/g;
P=mg;
Эти отношения напоминают известную из электротехники формулу закона Ома
U=I*R.
Изобразим полученные соотношения в виде следующих триад.
Такая
интерпретация полученных выражений принята потому, что по форме они
напоминают известные из механики Ньютона категории - массы и веса:
m=P/g;
P=mg;
Эти отношения напоминают известную из электротехники формулу закона Ома
U=I*R.
Изобразим полученные соотношения в виде следующих триад.
 рис. 3
На данном рисунке Символ Великого предела символизирует в системах разной
природы принцип самонормировки (приведением к Единице). Великий предел,
разворачивается в триаду, а уже триада порождает "собственное мироздание".
Кому-то из читателей это нагромождение вроде бы совершенно не связанных
физическими смыслами триад, покажется чушью. Однако эта чушь обладает
какой-то необъяснимой, с точки зрения "обыденного" здравого смысла"
мистикой. Но эта мистика, с точки зрения природных операционных механизмов
Единого закона эволюции двойственного отношения имеет совершенно очевидные
причины и порождает еще более совершенно очевидные следствия.
И эта "чушь" порождается триадой "Единица-ЯН-ИНЬ". В ней
нет физических смыслов, и потому эта идеальная триада отражает смыслы
всех физических триад (кварки-антикварки). Эти триады проявляются в
электромагнитных полях, в электрических сетях, и т.д.
И потому свойства этой триады, по образу и
подобию, может быть перенесено и на триаду экономической рентабельности.
Полагаю, что
данные аналогии могут оказаться полезной и для
профессиональных физиков, ибо она может дать ключ к более глубокому
пониманию инерционной и гравитационных масс, как в механике Ньютона, так и в
механике микромира, а также везде, где есть двойственное отношение (монада).
Ибо подобное триединство является всеобщим для "мирозданий" любой
природы.
1.3.2.
СИЛА
РЕНТАБЕЛЬНОСТИ
Перепишем теперь приведенное выше тождество в следующем виде
рис. 3
На данном рисунке Символ Великого предела символизирует в системах разной
природы принцип самонормировки (приведением к Единице). Великий предел,
разворачивается в триаду, а уже триада порождает "собственное мироздание".
Кому-то из читателей это нагромождение вроде бы совершенно не связанных
физическими смыслами триад, покажется чушью. Однако эта чушь обладает
какой-то необъяснимой, с точки зрения "обыденного" здравого смысла"
мистикой. Но эта мистика, с точки зрения природных операционных механизмов
Единого закона эволюции двойственного отношения имеет совершенно очевидные
причины и порождает еще более совершенно очевидные следствия.
И эта "чушь" порождается триадой "Единица-ЯН-ИНЬ". В ней
нет физических смыслов, и потому эта идеальная триада отражает смыслы
всех физических триад (кварки-антикварки). Эти триады проявляются в
электромагнитных полях, в электрических сетях, и т.д.
И потому свойства этой триады, по образу и
подобию, может быть перенесено и на триаду экономической рентабельности.
Полагаю, что
данные аналогии могут оказаться полезной и для
профессиональных физиков, ибо она может дать ключ к более глубокому
пониманию инерционной и гравитационных масс, как в механике Ньютона, так и в
механике микромира, а также везде, где есть двойственное отношение (монада).
Ибо подобное триединство является всеобщим для "мирозданий" любой
природы.
1.3.2.
СИЛА
РЕНТАБЕЛЬНОСТИ
Перепишем теперь приведенное выше тождество в следующем виде
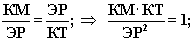 Это
выражение отражает
единичную силу рентабельности
(нормированная сила
рентабельности). Эта сила фиксирует достигнутое
состояние ЭР, т.е.
Это
выражение отражает
единичную силу рентабельности
(нормированная сила
рентабельности). Эта сила фиксирует достигнутое
состояние ЭР, т.е.
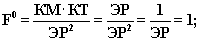 Это выражение означает, что всякий раз,
когда возникает рассогласование баланса между КМ и КТ, то проявляется Сила,
пропорциональная произведению КМ и КТ и обратно пропорциональной квадрату
ЭР. Однако,
следует помнить, что в данных тождествах операция умножения являются не
скалярной.
В самом общем
случае используется операция умножения ортогональных векторов.
Видите, по форме это выражение совпадает с известным из
механики Ньютона законом всемирного тяготения
Это выражение означает, что всякий раз,
когда возникает рассогласование баланса между КМ и КТ, то проявляется Сила,
пропорциональная произведению КМ и КТ и обратно пропорциональной квадрату
ЭР. Однако,
следует помнить, что в данных тождествах операция умножения являются не
скалярной.
В самом общем
случае используется операция умножения ортогональных векторов.
Видите, по форме это выражение совпадает с известным из
механики Ньютона законом всемирного тяготения
 .
1.3.3.
ЗАКОН ИНЕРЦИИ РЕНТАБЕЛЬНОСТИ АКТИВОВ
Из выражения для F0 следует ЭР=
F0. Это есть единичное плечо рычага
монады "КМ-КТ" (рис. 2). Таким образом, если плечо рычага
рентабельности не изменяется (ЭР=const), и
произведение КМ* КМ =сonst, то мы можем говорить об
единичной силе F0=1,
и, следовательно, в этом случае ЭР будет служить мерой силы инерции
экономической рентабельности, а
F0 будет отражать закон
инерции экономической рентабельности активов:
"Если на тело
(предприятие) не действуют внешние силы, приводящие к изменению КМ и КТ, то
тело (предприятие) движется под действием силы инерции (F0=const)".
И снова мы получаем аналогию с законом инерции механики Ньютона. Снова
забавное совпадение? А, может быть, это плоды
моего искаженного мышления?
Во всяком случае, из такого определения экономической рентабельности (ЭР0=
const)
следует, что
траектория
эволюции двойственного отношения, при постоянной ЭР определяется кривой,
показанной на рис. 1.
Очевидно, что при различных ЭР=const,
мы будем получать новые кривые, отражающие равновесное состояние между КМ и
КТ.
Выразим теперь жая теперь экономическую рентабельность через
инерционную и гравитационную массы рентабельности, мы получим .
1.3.3.
ЗАКОН ИНЕРЦИИ РЕНТАБЕЛЬНОСТИ АКТИВОВ
Из выражения для F0 следует ЭР=
F0. Это есть единичное плечо рычага
монады "КМ-КТ" (рис. 2). Таким образом, если плечо рычага
рентабельности не изменяется (ЭР=const), и
произведение КМ* КМ =сonst, то мы можем говорить об
единичной силе F0=1,
и, следовательно, в этом случае ЭР будет служить мерой силы инерции
экономической рентабельности, а
F0 будет отражать закон
инерции экономической рентабельности активов:
"Если на тело
(предприятие) не действуют внешние силы, приводящие к изменению КМ и КТ, то
тело (предприятие) движется под действием силы инерции (F0=const)".
И снова мы получаем аналогию с законом инерции механики Ньютона. Снова
забавное совпадение? А, может быть, это плоды
моего искаженного мышления?
Во всяком случае, из такого определения экономической рентабельности (ЭР0=
const)
следует, что
траектория
эволюции двойственного отношения, при постоянной ЭР определяется кривой,
показанной на рис. 1.
Очевидно, что при различных ЭР=const,
мы будем получать новые кривые, отражающие равновесное состояние между КМ и
КТ.
Выразим теперь жая теперь экономическую рентабельность через
инерционную и гравитационную массы рентабельности, мы получим
 Видите, отношение инерционной массы рентабельности к гравитационной массе по
форме снова совпадает с известным из механики Ньютона законом
всемирного тяготения
Таким образом, по аналогии с механикой Ньютона,
мы получили движущую силу экономической
рентабельности активов предприятия:
"Сила
рентабельности активов предприятия пропорциональна
произведению результата эксплуатации инвестиций (НРЭИ) и
Активов и обратно пропорционально квадрату Оборотов".
2.ЛОГИКА ФИНАНСОВОГО
МЕХАНИЗМА ПРЕДПРИЯТИЯ
2.1. ПРОИЗВОДЯЩИЕ
ФУНКЦИИ КАПИТАЛА ПРЕДПРИЯТИЯ
Из
приведенных выше тождеств можно сделать вывод о том, что рыночные отношения
спроса и предложения отражаются в экономике не только во взаимоотношениях
между товаром и деньгами (между капиталом-собственностью и
капиталом-функцией).
Далее, из
математики известно, что нелинейные зависимости могут быть
представлены в форме производящих функций. Представленные выше тождества,
видимо, в самом общем случае, также можно будет отразить в форме
производящих функций.
На странице "Преемственность",
рассматривая свойства производящих функций вида
Видите, отношение инерционной массы рентабельности к гравитационной массе по
форме снова совпадает с известным из механики Ньютона законом
всемирного тяготения
Таким образом, по аналогии с механикой Ньютона,
мы получили движущую силу экономической
рентабельности активов предприятия:
"Сила
рентабельности активов предприятия пропорциональна
произведению результата эксплуатации инвестиций (НРЭИ) и
Активов и обратно пропорционально квадрату Оборотов".
2.ЛОГИКА ФИНАНСОВОГО
МЕХАНИЗМА ПРЕДПРИЯТИЯ
2.1. ПРОИЗВОДЯЩИЕ
ФУНКЦИИ КАПИТАЛА ПРЕДПРИЯТИЯ
Из
приведенных выше тождеств можно сделать вывод о том, что рыночные отношения
спроса и предложения отражаются в экономике не только во взаимоотношениях
между товаром и деньгами (между капиталом-собственностью и
капиталом-функцией).
Далее, из
математики известно, что нелинейные зависимости могут быть
представлены в форме производящих функций. Представленные выше тождества,
видимо, в самом общем случае, также можно будет отразить в форме
производящих функций.
На странице "Преемственность",
рассматривая свойства производящих функций вида
P0(x)=1;
P1(x)=(1-x)-1=1-x+x2-x3+
...
P2(x)=(1-x)-2=1-2x+3x2-4x3+...
P3(x)=(1-x)-3=1-3x+6x2-10x3+...
P4(x)=(1-x)-4=1-5x+14x2-30x3+...
Применяя к
n-мерной производящей функции
Pi(x),
i=1,2,3,...оператор удвоенияG0(x),
мы получим следующие производящие функции
G0(x)=(1+х)1P0(x);
G1(x)=G0(x)P1(x)=G0(x)(1-x)-1
=1-2x+2x2-2x3+
...
G2(x)=G0(x)P2(x)=G0(x)(1-x)-2=1-3x+5x2-7x3+
...
G3(x)=G0(x)P3(x)=G0(x)(1-x)-3=1-4x+
9x2-16x3+
...
G4(х)=G0(x)P4(x)=G0(x)=(1-x)-4=1-5х+14х2-30х3+...
Отождествляя, например,
производящие функции
Pi(x),
i=1,2,3, с капиталом-функцией, а
производящие функции
Gi(x),
i=1,2,3,-c капиталом-функцией, мы
получим самое первое представление о двойной спирали эволюции капитала
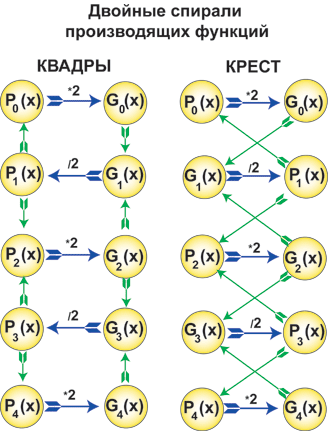 рис.
4
На странице "Русская матрица" мы показали,
что золотосеченные числа образуют "весы"
рис.
4
На странице "Русская матрица" мы показали,
что золотосеченные числа образуют "весы"
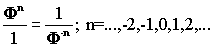 Такие "весы" имеются и
в приведенных на рис. 6 схемах. Так для
двойной спирали "крест" имеют место следующие пропорции
Такие "весы" имеются и
в приведенных на рис. 6 схемах. Так для
двойной спирали "крест" имеют место следующие пропорции
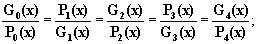 (*)
Из этих пропорций непосредственно можно получить все формулы для определения
любого члена двойной цепочки, например,
(*)
Из этих пропорций непосредственно можно получить все формулы для определения
любого члена двойной цепочки, например,
 В этих
двойных спиралях каждая из функций (Pn(x)
и Gn(х)) играет роль точки
бифуркации, в которой происходит раздвоение, или точкой синтеза (удвоение).
Каждая производящая функция является либо точкой синтеза (удвоение), либо точкой
бифуркации (раздвоение).
Из
рис. 6 видно, что правый столбец с спирали "крест" сформирован из иньской
цепочки. Здесь каждая производящая функция является точкой синтеза
(умножить-умножить-разделить)
В этих
двойных спиралях каждая из функций (Pn(x)
и Gn(х)) играет роль точки
бифуркации, в которой происходит раздвоение, или точкой синтеза (удвоение).
Каждая производящая функция является либо точкой синтеза (удвоение), либо точкой
бифуркации (раздвоение).
Из
рис. 6 видно, что правый столбец с спирали "крест" сформирован из иньской
цепочки. Здесь каждая производящая функция является точкой синтеза
(умножить-умножить-разделить)
 Вторая
спираль обладает уже янскими свойствами (умножить- разделить-разделить)
Вторая
спираль обладает уже янскими свойствами (умножить- разделить-разделить)
 Взаимоотношения между капиталом-собственностью (товар) и
капиталом-функцией (деньги) можно отразить теперь на следующих схемах.
Взаимоотношения между капиталом-собственностью (товар) и
капиталом-функцией (деньги) можно отразить теперь на следующих схемах.
 рис.
5
Данный рисунок отражает взаимоотношения между
финансовой деятельностью (деньги) деньгами и хозяйственной деятельностью
(товарами). Здесь товар (капитал-собственность) находится в иньской цепочке, а
деньги (капитал-функция) - в янской. Данные схемы отражают двойственную схему
формирования двойной экономической спирали, в соответствии с законами
сохранения зеркальной и зарядовой симметрии.
Двойная
цепочка "товар-деньги-товар-..."
на каждом этапе расширенного воспроизводства капитала
воспроизводит саму
себя, по образу и подобию", в соответствии с весами (*),
т.е. каждая пропорция отражает в себе финансово-хозяйственый рычаг расширенного
воспроизводства капитала.
Рассмотрим теперь
проявление этих рычагов в классическом финансовом менеджменте.
2.2. ЭФФЕКТ ФИНАНСОВОГО
РЫЧАГА
Эффект финансового рычага
(ЭФР) -это
приращение к рентабельности собственных средств. получаемое благодаря
использованию кредита, несмотря на платность последнего.
рис.
5
Данный рисунок отражает взаимоотношения между
финансовой деятельностью (деньги) деньгами и хозяйственной деятельностью
(товарами). Здесь товар (капитал-собственность) находится в иньской цепочке, а
деньги (капитал-функция) - в янской. Данные схемы отражают двойственную схему
формирования двойной экономической спирали, в соответствии с законами
сохранения зеркальной и зарядовой симметрии.
Двойная
цепочка "товар-деньги-товар-..."
на каждом этапе расширенного воспроизводства капитала
воспроизводит саму
себя, по образу и подобию", в соответствии с весами (*),
т.е. каждая пропорция отражает в себе финансово-хозяйственый рычаг расширенного
воспроизводства капитала.
Рассмотрим теперь
проявление этих рычагов в классическом финансовом менеджменте.
2.2. ЭФФЕКТ ФИНАНСОВОГО
РЫЧАГА
Эффект финансового рычага
(ЭФР) -это
приращение к рентабельности собственных средств. получаемое благодаря
использованию кредита, несмотря на платность последнего.
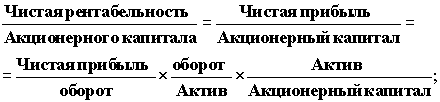 Заметьте, эта цепочка представляет собой ян-иньскую последовательность
пропорций, характеризующих обратную зависимость.
2.2.1. ПЕРВЫЙ СПОСОБ РАСЧЕТА
Эффект финансового рычага (ЭФР)
характеризуется двумя составляющими
Дифференциал=(2/3)(ЭР-СРСП)
Дифференциал не должен
быть отрицательным!
Это
разница между Экономической
Рентабельностью активов и
Средней
Расчетной
Ставкой
Процента по заемным
средствам. Коэффициент 2/3 учитывает отражает ставку налогообложения
(примерно 1/3) от диференциала.
Плечо Финансового Рычага (ПФР)-характеризует силу
воздействия финансового рычага
Заметьте, эта цепочка представляет собой ян-иньскую последовательность
пропорций, характеризующих обратную зависимость.
2.2.1. ПЕРВЫЙ СПОСОБ РАСЧЕТА
Эффект финансового рычага (ЭФР)
характеризуется двумя составляющими
Дифференциал=(2/3)(ЭР-СРСП)
Дифференциал не должен
быть отрицательным!
Это
разница между Экономической
Рентабельностью активов и
Средней
Расчетной
Ставкой
Процента по заемным
средствам. Коэффициент 2/3 учитывает отражает ставку налогообложения
(примерно 1/3) от диференциала.
Плечо Финансового Рычага (ПФР)-характеризует силу
воздействия финансового рычага
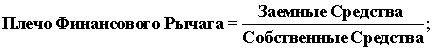 Теперь мы модем определить Уровень
ЭФР:
Теперь мы модем определить Уровень
ЭФР:
 Видите, мы здесь
непосредственно получили формулу "умножить-умножить-разделить", отражающую
иньскую (точка синтеза капитала) сущность ЭФР.
Э то
Первый способ расчета уровня ЭФР, который открывает широкие возможности
по определению безопасного объема заемных средств, расчету допустимых условий
кредитования, а в сочетании с формулой
РСС=2/3
ЭР +ЭФР
-и
по облегчению налогового бремени для предприятия.
Этот способ определяет условия обеспечения экономической безопасности не
только экономики предприятия, но эта формула годится и для того, чтобы ее
учитывали и при разработке концепции экономической безопасности России.
Разумный руководитель нее станет увеличивать любой ценой Плечо
Финансового Рычага, а будет регулировать Плечо рычага в зависимости от
Дифференциала.
Ну
как ту снова не вспомнить о принципах самоорганизации -целостность
(Единица), самодостаточность (2/3), саморегуляция, самовоспроизведение,
саморазвитие и самонормировка.
2.2.2. ВТОРОЙ СПОСОБ РАСЧЕТА
Приведем сначала некоторые основные определения.
Добавленная
Стоимость (ДС).
Если
из Стоимости Продукции (СП)
, произведенной предприятием ( а не только реализованной!) за тот или иной
период, вычесть Стоимость Потребленных
Материальных Средств Производства
(СПМС) (сырья, энергии и
пр.)ь и услуг других организаций, то получится Стоимость, которую
действительно добавили к стоимости сырья, энергии, услуг. Динамика ДС
свидетельствует о масштабах деятельности предприятия и его вкладе в создание
национального богатства. Особенно наглядно эта динамика будет проявляться,
если использовать относительные единицы (СПМС/СП).
Брутто-Результат-Эксплуатации Инвестиций (БРЭИ).
Вычитая из ДС Расходы по Оплате Труда (РОТ)
и все связанные с ней обязательные платежи
предприятия (по социальному страхованию, пенсионному обеспечению и проч.), а
также "налоговую накрутку", связанную с перерасходом норматива заработной
платы, т.е.
БРЭИ=ДС-РОТ.
БРЭИ
используется как один из основных промежуточных
результатов
финансово-хозяйственной деятельности. Представляя собой прибыль до вычета
амортизации, финансовых издержек по заемным средствам и налога на прибыль,
величина БРЭИ является первейшим показателем достаточности средств на покрытие
всех этих расходов (налоги-те же расходы). По удельному весу БРЭИ в
Добавленной Стоимости (ДС) . можноь судить об эффективности управления
предприятием и составить общее представление о потенциальной рентабельности и
гибкости предприятия.
Нетто-Результат-Эксплуатации Инвестиций (НРЭИ).
Это
прибыль до уплаты процентов за кредит и налога на прибыль.
Эффект
Финансового Рычага-
можно
трактовать и как процентное изменение чистой прибыли на каждую обыкновенную
акцию, порождаемое данным процентным изменением нетто-результата эксплуатации
инвестиций .
Такое восприятие ЭФР характерно в основном для американской школы финансового
менеджмента.
Видите, мы здесь
непосредственно получили формулу "умножить-умножить-разделить", отражающую
иньскую (точка синтеза капитала) сущность ЭФР.
Э то
Первый способ расчета уровня ЭФР, который открывает широкие возможности
по определению безопасного объема заемных средств, расчету допустимых условий
кредитования, а в сочетании с формулой
РСС=2/3
ЭР +ЭФР
-и
по облегчению налогового бремени для предприятия.
Этот способ определяет условия обеспечения экономической безопасности не
только экономики предприятия, но эта формула годится и для того, чтобы ее
учитывали и при разработке концепции экономической безопасности России.
Разумный руководитель нее станет увеличивать любой ценой Плечо
Финансового Рычага, а будет регулировать Плечо рычага в зависимости от
Дифференциала.
Ну
как ту снова не вспомнить о принципах самоорганизации -целостность
(Единица), самодостаточность (2/3), саморегуляция, самовоспроизведение,
саморазвитие и самонормировка.
2.2.2. ВТОРОЙ СПОСОБ РАСЧЕТА
Приведем сначала некоторые основные определения.
Добавленная
Стоимость (ДС).
Если
из Стоимости Продукции (СП)
, произведенной предприятием ( а не только реализованной!) за тот или иной
период, вычесть Стоимость Потребленных
Материальных Средств Производства
(СПМС) (сырья, энергии и
пр.)ь и услуг других организаций, то получится Стоимость, которую
действительно добавили к стоимости сырья, энергии, услуг. Динамика ДС
свидетельствует о масштабах деятельности предприятия и его вкладе в создание
национального богатства. Особенно наглядно эта динамика будет проявляться,
если использовать относительные единицы (СПМС/СП).
Брутто-Результат-Эксплуатации Инвестиций (БРЭИ).
Вычитая из ДС Расходы по Оплате Труда (РОТ)
и все связанные с ней обязательные платежи
предприятия (по социальному страхованию, пенсионному обеспечению и проч.), а
также "налоговую накрутку", связанную с перерасходом норматива заработной
платы, т.е.
БРЭИ=ДС-РОТ.
БРЭИ
используется как один из основных промежуточных
результатов
финансово-хозяйственной деятельности. Представляя собой прибыль до вычета
амортизации, финансовых издержек по заемным средствам и налога на прибыль,
величина БРЭИ является первейшим показателем достаточности средств на покрытие
всех этих расходов (налоги-те же расходы). По удельному весу БРЭИ в
Добавленной Стоимости (ДС) . можноь судить об эффективности управления
предприятием и составить общее представление о потенциальной рентабельности и
гибкости предприятия.
Нетто-Результат-Эксплуатации Инвестиций (НРЭИ).
Это
прибыль до уплаты процентов за кредит и налога на прибыль.
Эффект
Финансового Рычага-
можно
трактовать и как процентное изменение чистой прибыли на каждую обыкновенную
акцию, порождаемое данным процентным изменением нетто-результата эксплуатации
инвестиций .
Такое восприятие ЭФР характерно в основном для американской школы финансового
менеджмента.
 или, после преобразований, получаем
или, после преобразований, получаем
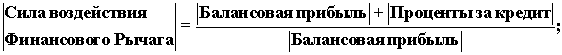
Если балансовую прибыль связать с
Результатом
Хозяйственной
Деятельности
предприятия (РХД), а проценты за кредит связать с
Результатами
Финансовой
Деятельности предприятия (РФД), связанной с обслуживанием заемных средств, то
числитель будет отражать результат финансово-хозяйственной деятельности
предприятия. Заменяя аддитивную операцию на мультипликативную, мы получим
показатель финансово-хозяйственной деятельности в относительных единицах (РФД/РХД).
Подставляя это значение в последнее выражение, мы получим "обратную" формулу
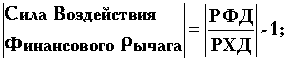 Руководители
предприятия должны помнить, что
ЧЕМ
БОЛЬШЕ СИЛА ВОЗДЕЙСТВИЯ ФИНАНСОВОГО РЫЧАГА, ТЕМ БОЛЬШИЙ РИСК, СВЯЗАННЫЙ С
ПРЕДПРИЯТИЕМ:
1.
Возрастает риск невозмещенного кредита с процентами для банкира;
2.Ворастает риск падения дивиденда и курса акций для инвестора.
Из краткого
рассмотрения логики механизмов финансового менеджмента видно, что эта логика
лежит в русле логики Единого закона эволюции двойственного
отношения. В финансовом менеджменте таким двойственным отношением является
монада "РФД-РХД", а Великий Предел этой монады отражает
Результаты
Финансово-Хозяйственной
Деятельности предприятия
(РФХД)
РФХД=РФД*РХД.
2.3. ЭФФЕКТ ОПЕРАЦИОННОГО
РЫЧАГА
Если ЭФР отражает в себе риски,
связанные с заимствованию финансовых средств, то эффект операционного рычага
отражает предпринимательские риски.
Данный эффект используется
в интересах регулирования массы и
динамики прибыли и определения "финансовой прочности" предприятия.
Рассматривая зависимости, связанные с затратами и их влиянием на прибыль,
специалисты пришли к выводу о том, что смешанные затраты (постоянные +
переменные) порождают феномен, который и называют собственно эффектом
производственного (операционного) рычага (ЭОР):
"Любое изменение выручки от реализации порождает
еще
более сильное изменение прибыли".
Смысл
ЭОР можно пояснить на следующем примере из книги Е.Стояновой.
Руководители
предприятия должны помнить, что
ЧЕМ
БОЛЬШЕ СИЛА ВОЗДЕЙСТВИЯ ФИНАНСОВОГО РЫЧАГА, ТЕМ БОЛЬШИЙ РИСК, СВЯЗАННЫЙ С
ПРЕДПРИЯТИЕМ:
1.
Возрастает риск невозмещенного кредита с процентами для банкира;
2.Ворастает риск падения дивиденда и курса акций для инвестора.
Из краткого
рассмотрения логики механизмов финансового менеджмента видно, что эта логика
лежит в русле логики Единого закона эволюции двойственного
отношения. В финансовом менеджменте таким двойственным отношением является
монада "РФД-РХД", а Великий Предел этой монады отражает
Результаты
Финансово-Хозяйственной
Деятельности предприятия
(РФХД)
РФХД=РФД*РХД.
2.3. ЭФФЕКТ ОПЕРАЦИОННОГО
РЫЧАГА
Если ЭФР отражает в себе риски,
связанные с заимствованию финансовых средств, то эффект операционного рычага
отражает предпринимательские риски.
Данный эффект используется
в интересах регулирования массы и
динамики прибыли и определения "финансовой прочности" предприятия.
Рассматривая зависимости, связанные с затратами и их влиянием на прибыль,
специалисты пришли к выводу о том, что смешанные затраты (постоянные +
переменные) порождают феномен, который и называют собственно эффектом
производственного (операционного) рычага (ЭОР):
"Любое изменение выручки от реализации порождает
еще
более сильное изменение прибыли".
Смысл
ЭОР можно пояснить на следующем примере из книги Е.Стояновой.
 рис.
6
Из этого графического способа определения порога рентабельности видно, что
каждая единица товара, начиная с 3822, будет приносить прибыль.
Из
рисунка непосредственно видно, что убытки и прибыль являются плечами
соответствующих производственных рычагов. И в относительных единицах они будут
выражаться пропорцией
рис.
6
Из этого графического способа определения порога рентабельности видно, что
каждая единица товара, начиная с 3822, будет приносить прибыль.
Из
рисунка непосредственно видно, что убытки и прибыль являются плечами
соответствующих производственных рычагов. И в относительных единицах они будут
выражаться пропорцией
 В левой части отношение будет отражать долю прибыли
от результатов финансово-хозяйственной деятельности, принятых за Единицу. Правая
часть отражает обратную пропорцию для убытков (антиприбыль).
Это
равенство будет иметь место в единственной точке -точке безубыточности.
И мы снова выходим на "затратные" и
"доходные" производящие функции ресурсов (O финансах),
отражающие процессы саморазвития предприятия.
В левой части отношение будет отражать долю прибыли
от результатов финансово-хозяйственной деятельности, принятых за Единицу. Правая
часть отражает обратную пропорцию для убытков (антиприбыль).
Это
равенство будет иметь место в единственной точке -точке безубыточности.
И мы снова выходим на "затратные" и
"доходные" производящие функции ресурсов (O финансах),
отражающие процессы саморазвития предприятия.
 рис.
7
Данная схема отражает
тривиальную, с точки зрения Единого закона, истину о двойственности
финансового и операционного рычагов и отражает качественно-количественную
оценку их воздействия на каждом финансово-хозяйственном обороте.
Не приводя расчетные формулы, отметим, что
Сила Воздействия Операционного Рычага указывает на
степень предпринимательского риска, связанного с данной фирмой:
чем больше Сила Воздействия Операционного Рычага, тем больше
предпринимательский риск.
Запас финансовой прочности
предприятия определяется разностью между выручкой от реализации и порогом
рентабельности (точкой безубыточности).
РЕЗЮМЕ
1. На многих страницах
сайта постоянно напоминается, что предметом исследования милогии являются не
Объекты и Субъекты определенной природы, рассматриваемый в рамках
существующих научных дисциплин и на основе изучения свойств и
взаимоотношений между Объектами и Субъектами выводятся законы и
закономерности той или иной прикладной науки. В милогии отсутствуют
собственные Объекты и Субъекты исследования. В основе милогии лежат
отношения между Объектами и Субъектами любой природы. Эти отношения
порождаются природными операционными механизмами Единого закона эволюции
двойственного отношения и являются всеобщими.
2. Поэтому из
краткого анализа логики механизмов финансового менеджмента следует осознать,
что здесь речь идет, прежде всего, не о финансовом менеджменте, как
научной дисциплине, а о том, что природные операционные механизмы
Единого закона проявляют себя и в финансовом менеджменте.
Именно с этих позиций
следует рассматривать содержание этой, а также многих других страниц.
3. Сегодня многие ученые осознают объективность Единого Знания.
Физики усиленно создают теорию Единого поля, у химиков уже есть почти
законченная Единая теория химических элементов, которая находит свое
отражение в Периодической системе химических элементов. В мире элементарных
частиц тоже начинают просматриваться контуры Единого знания. И экономическая
наука не является исключением из общего правила. Единый закон не знает
исключений. Для него нет исключений. И если специалисты в сфере финансового
менеджмента осознают это, то финансовый менеджмент выйдет на качественно
новый уровень развития.
рис.
7
Данная схема отражает
тривиальную, с точки зрения Единого закона, истину о двойственности
финансового и операционного рычагов и отражает качественно-количественную
оценку их воздействия на каждом финансово-хозяйственном обороте.
Не приводя расчетные формулы, отметим, что
Сила Воздействия Операционного Рычага указывает на
степень предпринимательского риска, связанного с данной фирмой:
чем больше Сила Воздействия Операционного Рычага, тем больше
предпринимательский риск.
Запас финансовой прочности
предприятия определяется разностью между выручкой от реализации и порогом
рентабельности (точкой безубыточности).
РЕЗЮМЕ
1. На многих страницах
сайта постоянно напоминается, что предметом исследования милогии являются не
Объекты и Субъекты определенной природы, рассматриваемый в рамках
существующих научных дисциплин и на основе изучения свойств и
взаимоотношений между Объектами и Субъектами выводятся законы и
закономерности той или иной прикладной науки. В милогии отсутствуют
собственные Объекты и Субъекты исследования. В основе милогии лежат
отношения между Объектами и Субъектами любой природы. Эти отношения
порождаются природными операционными механизмами Единого закона эволюции
двойственного отношения и являются всеобщими.
2. Поэтому из
краткого анализа логики механизмов финансового менеджмента следует осознать,
что здесь речь идет, прежде всего, не о финансовом менеджменте, как
научной дисциплине, а о том, что природные операционные механизмы
Единого закона проявляют себя и в финансовом менеджменте.
Именно с этих позиций
следует рассматривать содержание этой, а также многих других страниц.
3. Сегодня многие ученые осознают объективность Единого Знания.
Физики усиленно создают теорию Единого поля, у химиков уже есть почти
законченная Единая теория химических элементов, которая находит свое
отражение в Периодической системе химических элементов. В мире элементарных
частиц тоже начинают просматриваться контуры Единого знания. И экономическая
наука не является исключением из общего правила. Единый закон не знает
исключений. Для него нет исключений. И если специалисты в сфере финансового
менеджмента осознают это, то финансовый менеджмент выйдет на качественно
новый уровень развития.
|


 "Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг). М.И. Беляев, 2015г,©
"Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг). М.И. Беляев, 2015г,©


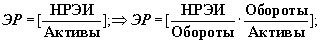
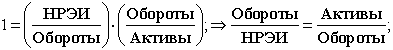 ,
,