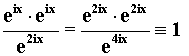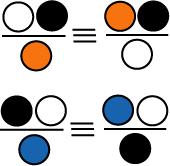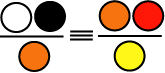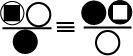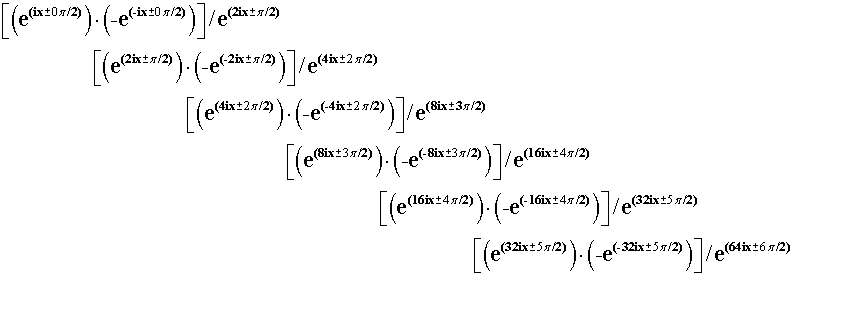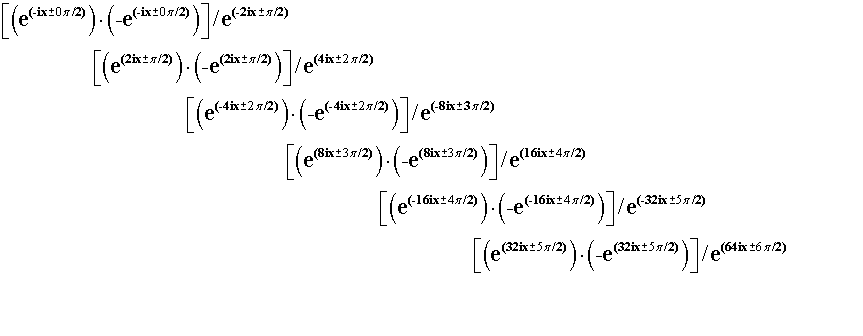ЗАКОНЫ ЭВОЛЮЦИИ
МАТЕРИИ И ДУХА
1. МОНАДНАЯ МЕХАНИКА
Поскольку
монада и монадные семейства отражают свойства Единого закона, то и
монадные законы должны отражать законы сохранения физики материи, в том
числе и законы механики.
Так,
из механики Ньютона известны три самых фундаментальных закона
Первый закон Ньютона:
Материальная точка в отсутствие действия на нее сил или при взаимном
уравновешивании последних находится в состоянии покоя или равномерного
прямолинейного движения. В монадной механике этот закон отражает
закон сохранения
монады, ее стабильное состояние в той или иной фазе
эволюции монады. Содержание этого закона аналогично содержанию закону Ньютона,
которым определяются инерциальные системы отсчета. Для монады такой
инерциальной системой отсчета являются собственные пространства. Напомним, что в
отличие от инерциальных систем собственное пространство содержит дискретных
набор собственных значений (локальных констант), определяющий
соответствующие свойства объекта, связанного с инерциальной системой отсчета.
Особо следует отметить, что
все монадные законы будут справедливы только для собственных монадных
пространств. Поскольку каждое собственное пространство характеризуется и
собственным временем, которое входит в состав набора собственных значений
этого пространства, то. следовательно, в рамках монадологии и пространство и
время являются относительными и квантованными (дискретными).
Второй закон Ньютона:
Скорость изменения импульса
p
материальной точки равна действующей на нее силе, т.е.

где
m,t,
v,a, обозначают
соответственно массу, время и вектора скорости и ускорения.
В монадной
механике этот закон отражает процесс фазового перехода монады из
одного состояния в другое.
Третий закон Ньютона:
Две материальные точки действуют друг на друга с силами
F1
и
F2, которые
числено равны и направлены в противоположные стороны вдоль прямой,
соединяющей эти точки:
F1=
- F2
Нетрудно понять, что этот закон определяет закон сохранения монады:
силы Ян и Инь
равны по величине, но противоположны по направлению.
2.
О МОНАДНОМ УРАВНЕНИИ УНИВЕРСАЛЬНОГО
ЗАКОНА
Многие
читатели, видимо, могут подумать, что сейчас они, наконец, увидят ту самую
заветную формулу, которая включает в себя все формулы и все уравнения, во всех
мирах и вселенных.
Что поделаешь, сила инерции мышления столь велика, что все мы привыкли думать,
что наша математика способна на любой "подвиг". Но. к сожалению, существующие
математические методы, несмотря на их чрезвычайную развитость, неспособны пока
выразить Единый закон эволюции двойственного отношения (монады), порождающего
янские и иньские эволюционные потоки, пока не способны к такому подвигу.
Поэтому основное внимание будет уделяться принципаам, в соответствии с которыми
будут формироваться те или иные эволюционные потоки.
Определим монадные кварки как следующие базисные функции.
 ,
где
к характеризует
номер монадной вершины.
Учитывая перенормировочные свойства креста,
означающие, что при переходе на другую
перекладину креста необходимо переходить с
операции умножения на операцию деления,
которая осуществляет нормирование
полученной триады и равносильна смене знака показателя
экспоненциальной функции, задача
нахождения универсального
уравнение эволюции двойственной пары, как
для пространственной, так и в проекциях модели этого уравнения на плоскость
гексады существенно упрощается.
Это замкнутая цепочка умножения друг на
друга, с последующим делением отражает
единичную элатичность экспоненциальных базисных
функций. При этом для пространственной
модели каждое последующее умножение
приводит к сдвигу фазы результирующей экспоненциальной функции на угол ,
где
к характеризует
номер монадной вершины.
Учитывая перенормировочные свойства креста,
означающие, что при переходе на другую
перекладину креста необходимо переходить с
операции умножения на операцию деления,
которая осуществляет нормирование
полученной триады и равносильна смене знака показателя
экспоненциальной функции, задача
нахождения универсального
уравнение эволюции двойственной пары, как
для пространственной, так и в проекциях модели этого уравнения на плоскость
гексады существенно упрощается.
Это замкнутая цепочка умножения друг на
друга, с последующим делением отражает
единичную элатичность экспоненциальных базисных
функций. При этом для пространственной
модели каждое последующее умножение
приводит к сдвигу фазы результирующей экспоненциальной функции на угол
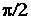 .
Для
уравнения в проекциях на плоскость гексады
сдвиг фазы результирующей
экспоненциальной функции будет равен .
Для
уравнения в проекциях на плоскость гексады
сдвиг фазы результирующей
экспоненциальной функции будет равен  .
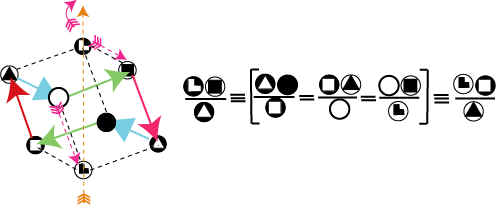
Экспоненциальные монадные семейства
занимают особую роль и значение в
формировании Мироздания. Применительно к проекции экспоненциальных
базисных функций на плоскость гексады (эта
плоскость ортогональна оси вращения
монадной формы, рис. 27), мы получим
следующие правила обхода монадной
формы по кресту, без учета сдвигов по
фазе и отождествляя исходную и конечную
экспоненциальные триады с цветами радуги,
мы получим весь спектр частиц,
характеризующих свойства монадных
частиц как экспоненциального семейства,
так и цветов радуги. .
Экспоненциальные монадные семейства
занимают особую роль и значение в
формировании Мироздания. Применительно к проекции экспоненциальных
базисных функций на плоскость гексады (эта
плоскость ортогональна оси вращения
монадной формы, рис. 27), мы получим
следующие правила обхода монадной
формы по кресту, без учета сдвигов по
фазе и отождествляя исходную и конечную
экспоненциальные триады с цветами радуги,
мы получим весь спектр частиц,
характеризующих свойства монадных
частиц как экспоненциального семейства,
так и цветов радуги.
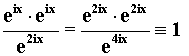
 Это и есть монадное уравнение
ЕДИНОГО УНИВЕРСАЛЬНОГО
ПЕРИОДИЧЕСКОГО ЗАКОНА ЭВОЛЮЦИИ ЖИВОЙ И
НЕЖИВОЙ МАТЕРИИ, отражающего функциональные
аспекты эволюции монады.
Посмотрите, триадные частицы
самонормируются!!!.
Они молча кричат о том, что в мироздании нет числа больше Единицы.
Это и есть монадное уравнение
ЕДИНОГО УНИВЕРСАЛЬНОГО
ПЕРИОДИЧЕСКОГО ЗАКОНА ЭВОЛЮЦИИ ЖИВОЙ И
НЕЖИВОЙ МАТЕРИИ, отражающего функциональные
аспекты эволюции монады.
Посмотрите, триадные частицы
самонормируются!!!.
Они молча кричат о том, что в мироздании нет числа больше Единицы.
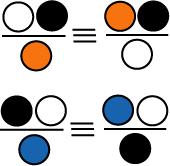 Последние монадные тождества показывают
сущность процессов, происходящих при
вращении монады по часовой и против часовой
стрелке. Эти тождества показывают, как
изначально двойственное отношение рождает
первую монадную триаду, свой первый закон
сохранения, свой первый "проявленный мир",
в котором изначальные черный и белый цвета
уже отсутствуют. Нетрудно видеть, что
исходная и конечная триады являются
зеркальными отпечатками друг друга, но
сдвинутыми друг относительно друга на одну
позицию.
Эти триады характеризуют замкнутый цикл
эволюции двойственного отношения в рамках
своего собственного семейства. Начальная и
конечная триады двойственного отношения
сдвинуты друг относительно друга на одну
позицию и являются зеркальным отпечатком
друг друга. Однако, возможен и другой
вариант эволюции двойственного отношения.
В этом случае происходит фазовый переход в
другое собственное пространство.
Последние монадные тождества показывают
сущность процессов, происходящих при
вращении монады по часовой и против часовой
стрелке. Эти тождества показывают, как
изначально двойственное отношение рождает
первую монадную триаду, свой первый закон
сохранения, свой первый "проявленный мир",
в котором изначальные черный и белый цвета
уже отсутствуют. Нетрудно видеть, что
исходная и конечная триады являются
зеркальными отпечатками друг друга, но
сдвинутыми друг относительно друга на одну
позицию.
Эти триады характеризуют замкнутый цикл
эволюции двойственного отношения в рамках
своего собственного семейства. Начальная и
конечная триады двойственного отношения
сдвинуты друг относительно друга на одну
позицию и являются зеркальным отпечатком
друг друга. Однако, возможен и другой
вариант эволюции двойственного отношения.
В этом случае происходит фазовый переход в
другое собственное пространство.

 Рис.1
Нетрудно видеть, что начальный и конечный
"отпечатки" двойственной пары
являются зеркальным отражением друг друга,
уже без сдвига по фазе. Рисунок 1 обладает еще одним важным свойством. Любые две
соседних триады с способны порождать собственные гексады эволюции,
собственный спектр цветов радуги.
Рис.1
Нетрудно видеть, что начальный и конечный
"отпечатки" двойственной пары
являются зеркальным отражением друг друга,
уже без сдвига по фазе. Рисунок 1 обладает еще одним важным свойством. Любые две
соседних триады с способны порождать собственные гексады эволюции,
собственный спектр цветов радуги.
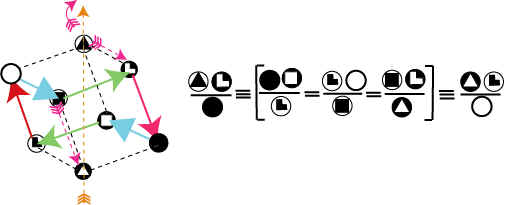
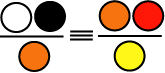 Поскольку
любые две соседние триады в этих тождественных
пропорциях зеркально симметричны, то
одноименные монадные кварки будут иметь разный
цвет и тем самым создают основу для формирования
новой совершенной формы.
Монадное уравнение характеризует очень
важные свойства монады.
Заменяя, например, в каждой монадной триаде
монадные кварки на экспоненцильные, мы будем
получать нормированные монадные частицы
вида
Поскольку
любые две соседние триады в этих тождественных
пропорциях зеркально симметричны, то
одноименные монадные кварки будут иметь разный
цвет и тем самым создают основу для формирования
новой совершенной формы.
Монадное уравнение характеризует очень
важные свойства монады.
Заменяя, например, в каждой монадной триаде
монадные кварки на экспоненцильные, мы будем
получать нормированные монадные частицы
вида
 Из этого монадного уравнения видно, что
при использовании экспоненциальных
кварков тождественность обхода по кресту
предполагает увеличение
экспоненциальных "вибраций" , т.е.
будут справедливы преобразования
Из этого монадного уравнения видно, что
при использовании экспоненциальных
кварков тождественность обхода по кресту
предполагает увеличение
экспоненциальных "вибраций" , т.е.
будут справедливы преобразования
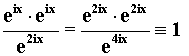 При
достижении высших для данной монадной
формы вибраций рожденная в результате
последнего "акта крещения" монадная
частица оказывается способной
преодолеть "вакуумный барьер",
разделяющего ее от семейства с более
высокими "вибрациями".
Из
монадного уравнения непосредственно видна
взаимосвязь белого и черного цветов и в
какой последовательности рождаются
цвета радуги. Очевидно, что полученное
уравнение допускает тождественные
преобразования.
Монадное
уравнение позволяет в самой общей форме
сформулировать самый сокровенный закон
Вселенной -
Единый Периодический закон эволюции живой
и неживой материи:
"Свойства
любого материального или духовного объекта
(процесса, явления, и т.д.), находятся в
периодической зависимости от свойств
самодостаточного двойственного отношения (монады),
эволюционные потоки которого (которой) порождают События и Перемены, в соответствии с алгоритмами
порождения триграмм и гексаграмм Книги Перемен".
Это определение является не полным. Это всего лишь самое первое представление.
3. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭВОЛЮЦИИ МОНАДНЫХ СЕМЕЙСТВ
Приведенные выше свойства монадных
семейств характеризуют двойственный
исход эволюции монадных частиц. Или в следующее
семейство с более высоким уровнем иерархии,
или назад, реализуя замкнутый цикл
эволюции. В любом случае эволюция
происходит путем последовательных обходов "по
кресту", выполняя последовательные операции умножения и
деления, начальная триада трансформируется
в своего зеркального двойника, но уже
принадлежащего другому семейству.
Рассмотрим вначале периодические
законы эволюции монадных семейств.
3.1.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ ДУАДНЫХ СЕМЕЙСТВ
Выбирая
из наборов монадных частиц, рассмотренных
выше, то или иное двойственное отношение, мы
получим дуальные семейства,
характеризуемые следующими свойствами
1.
Для двойственной пары
При
достижении высших для данной монадной
формы вибраций рожденная в результате
последнего "акта крещения" монадная
частица оказывается способной
преодолеть "вакуумный барьер",
разделяющего ее от семейства с более
высокими "вибрациями".
Из
монадного уравнения непосредственно видна
взаимосвязь белого и черного цветов и в
какой последовательности рождаются
цвета радуги. Очевидно, что полученное
уравнение допускает тождественные
преобразования.
Монадное
уравнение позволяет в самой общей форме
сформулировать самый сокровенный закон
Вселенной -
Единый Периодический закон эволюции живой
и неживой материи:
"Свойства
любого материального или духовного объекта
(процесса, явления, и т.д.), находятся в
периодической зависимости от свойств
самодостаточного двойственного отношения (монады),
эволюционные потоки которого (которой) порождают События и Перемены, в соответствии с алгоритмами
порождения триграмм и гексаграмм Книги Перемен".
Это определение является не полным. Это всего лишь самое первое представление.
3. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭВОЛЮЦИИ МОНАДНЫХ СЕМЕЙСТВ
Приведенные выше свойства монадных
семейств характеризуют двойственный
исход эволюции монадных частиц. Или в следующее
семейство с более высоким уровнем иерархии,
или назад, реализуя замкнутый цикл
эволюции. В любом случае эволюция
происходит путем последовательных обходов "по
кресту", выполняя последовательные операции умножения и
деления, начальная триада трансформируется
в своего зеркального двойника, но уже
принадлежащего другому семейству.
Рассмотрим вначале периодические
законы эволюции монадных семейств.
3.1.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ ДУАДНЫХ СЕМЕЙСТВ
Выбирая
из наборов монадных частиц, рассмотренных
выше, то или иное двойственное отношение, мы
получим дуальные семейства,
характеризуемые следующими свойствами
1.
Для двойственной пары 

2.
Для двойственной пары 
3.
Для двойственной пары 
4.
Для двойственной пары 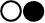

3.2. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ТРИПЛЕТНЫХ СЕМЕЙСТВ
Триплетные
монадные семейства частиц будут
характеризоваться другой структурой
двойственных отношений. Здесь
разноцветные одноименные кварки будут
являться уже не антикварками, а
взаимодополнительными одноименными
кварками. Для двойственной пары  триплетное семейство будет иметь вид
триплетное семейство будет иметь вид

Особенность данного семейства монадных
частиц заключается в том, что здесь имеется
единственная двойственная пара (монада),
кварки которой размещаются на диагонали
монадной формы. Поэтому внутренняя
структура этой монады будет изначально
тройственной, т.е. состав исходной триады
будет обязательно входить два одноименных,
но разноцветных монадных кварка.
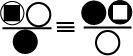 Из смысла
этого тождества, характеризующего
свойства триплетной монады, видно, что это
двойственное отношение в совокупности
образует крест - основу генетического
монадного кода.
4. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭКСПОНЕНЦИАЛЬНЫХ СЕМЕЙСТВ
4.1. ЭКСПОНЕНЦИАЛЬНЫЕ СЕМЕЙСТВА
Выбирая в качестве базисных функций
двойственную пару
Из смысла
этого тождества, характеризующего
свойства триплетной монады, видно, что это
двойственное отношение в совокупности
образует крест - основу генетического
монадного кода.
4. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭКСПОНЕНЦИАЛЬНЫХ СЕМЕЙСТВ
4.1. ЭКСПОНЕНЦИАЛЬНЫЕ СЕМЕЙСТВА
Выбирая в качестве базисных функций
двойственную пару 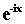 и и
 , мы получим
следующее семейство экспоненциальных
частиц , мы получим
следующее семейство экспоненциальных
частиц

Каждое триадное выражение в этом
семействе отражает эластичность соответствующей экспоненциальной двойственной
пары.
Выбирая
другие двойственные пары, мы получим другие
экспоненциальные семейства частиц. Если
данную двойственную пару
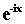 и
и  отождествить с физическими кварками s
и d, то
станет ясной причина физической странности кварка
s. Эти
кварки являются двойственными и
взаимодополняющими полюсами единого
двойственного отношения, порождающего
соответствующее семейство монадных частиц.
Данное экспоненциальное семейство не
претендует на истину в последней инстанции.
Оно описывает только принципы сопряжения.
Во-первых, при формировании очередного "рычага"
креста каждый экспоненциальный
кварк сдвигается по фазе на угол
отождествить с физическими кварками s
и d, то
станет ясной причина физической странности кварка
s. Эти
кварки являются двойственными и
взаимодополняющими полюсами единого
двойственного отношения, порождающего
соответствующее семейство монадных частиц.
Данное экспоненциальное семейство не
претендует на истину в последней инстанции.
Оно описывает только принципы сопряжения.
Во-первых, при формировании очередного "рычага"
креста каждый экспоненциальный
кварк сдвигается по фазе на угол
 .
В результате вектор экспоненциальной
частицы после обхода монадной формы
совпадает с первоначальным только после
фазового сдвига на угол .
В результате вектор экспоненциальной
частицы после обхода монадной формы
совпадает с первоначальным только после
фазового сдвига на угол  .
Правила порождения экспоненциальных
двойственных отношений, свойства каждой
экспоненциального кварка и частицы,
являются самыми фундаментальными
аспектами проявления Единого
Универсального закона эволюции живой и
неживой материи.
4.2. ДУАДНЫЕ
СЕМЕЙСТВА
Цепочку частиц, из
которых формируются дуальные пары монадного семейства можно записать в виде
следующей цепной дроби .
Правила порождения экспоненциальных
двойственных отношений, свойства каждой
экспоненциального кварка и частицы,
являются самыми фундаментальными
аспектами проявления Единого
Универсального закона эволюции живой и
неживой материи.
4.2. ДУАДНЫЕ
СЕМЕЙСТВА
Цепочку частиц, из
которых формируются дуальные пары монадного семейства можно записать в виде
следующей цепной дроби

Рис.2
Выбирая в качестве базисных монадные
экспоненциальные функции

можно построить, например, из них
следующее дуальное семейство, полагая, что экспоненциальные кварки и антикварки
характеризуются разной спиральностью, а кварки с разыми знаками характеризуют
их цвет. Тогда. из смысла рисунка 2.
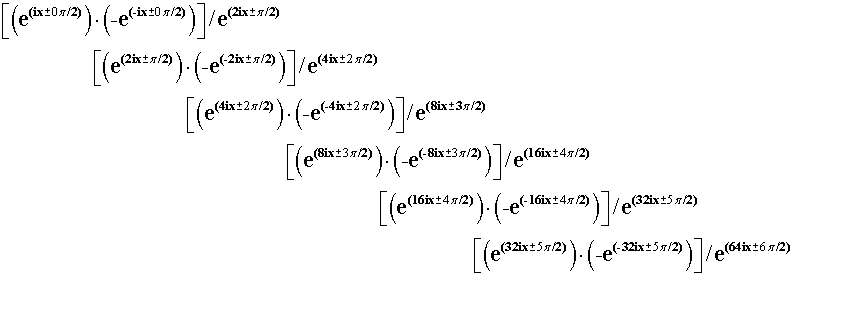
Рис. 3
Особенность формирования дуальных
частиц, приведенной на схеме, заключается в том, что операция деления
осуществляется на ту же самую частицу, но имеющую удвоенный аргумент, как бы
переводя экспоненциальный кварк в новое измерение. Анализ рисунков 1-3 позволяет понять,
как осуществляется нормирование экспоненциальных монадных частиц:
1.
Вначале формируется числитель цепной дроби путем сопряжения двух монадных частиц
с одним и тем же спином (операция умножения). Эта операция производит
перенормировку числителя в 1.
2. Затем
осуществляется переход ко второй перекладине креста - числитель делится на
монадную частицу, сдвинутую по фазе но вторая частица сдвинута по фазе
относительно числителя на  , как бы
иллюстрируя переход в другое измерение, в другую квадру (операция деления).
3. Далее происходит
нормировка знаменателя (операция умножения), и т.д.
4.3. ТРИПЛЕТНЫЕ
СЕМЕЙСТВА
Цепочку монадных частиц этого семейства
можно записать в следующем виде , как бы
иллюстрируя переход в другое измерение, в другую квадру (операция деления).
3. Далее происходит
нормировка знаменателя (операция умножения), и т.д.
4.3. ТРИПЛЕТНЫЕ
СЕМЕЙСТВА
Цепочку монадных частиц этого семейства
можно записать в следующем виде
 Особенность этого
семейства заключается в том, что здесь числитель также нормируется, но для этого
используются уже три экспоненциальных кварка. На приведенной ниже показана схеме
нормировка в единичную частицу происходит при операции деления ( при
переходе к следующей "перекладине" креста).
Особенность этого
семейства заключается в том, что здесь числитель также нормируется, но для этого
используются уже три экспоненциальных кварка. На приведенной ниже показана схеме
нормировка в единичную частицу происходит при операции деления ( при
переходе к следующей "перекладине" креста).
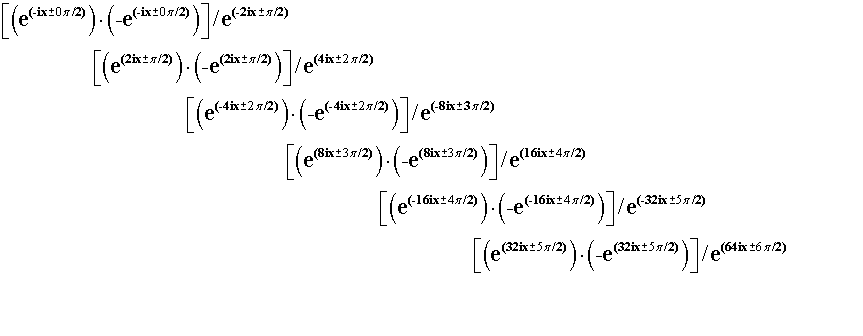 Особенность формирования триплетного
экспоненциального семейства заключается в том, что одноименные кварки
умножаются с противоположным спином, т.е. эти кварки одноименные, но
разноцветные.
Насколько эти схемы соответствуют
действительным триплетным группировкам?
5.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ МИКРОМИРА
5.1.
ДУАДНЫЕ СЕМЕЙСТВА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Особенность формирования триплетного
экспоненциального семейства заключается в том, что одноименные кварки
умножаются с противоположным спином, т.е. эти кварки одноименные, но
разноцветные.
Насколько эти схемы соответствуют
действительным триплетным группировкам?
5.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ МИКРОМИРА
5.1.
ДУАДНЫЕ СЕМЕЙСТВА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Для
дуадного семейства элементарных частиц,
порожденных триадой <s,d,u> мы получим
следующее семейство

Это
семейство характеризует Периодический
закон эволюции семейства, известного в
физике как мезонное. Заменяя
в этом семействе кварки на их антиподы,
мы получим дуальное семейство мезонных античастиц.
5.2. ТРИПЛЕТНЫЕ СЕМЕЙСТВА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ

Для
получения триплетного семейства
античастиц достаточно в данном семействе
заменить кварки на антикварки. В физике
элементарных частиц этому семейству
соответствуют барионы.
Ниже, на страницах сайта будет показано, что
Периодический закон эволюции химических
элементов является частью Единой
Периодической системы эволюции неживой и
живой материи.
5.3. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ МАТЕРИИ
Периодические законы микромира: "Масса
и другие свойства элементарных частиц
находятся в периодической зависимости от
свойств двойственного отношения (монады),
характеризующего сущность того или иного
семейства элементарных частиц".
Периодический закон химических элементов. Открыт
Д.И. Менделеевым.
Периодические законы макромира: «Свойства
звездных элементов находятся в
периодической зависимости от свойств
самодостаточного двойственного отношения,
характеризующего их сущность (энергетическая
оболочка- масса)».
6. ПЕРИОДИЧЕСКИЙ ЗАКОНЫ
ЭВОЛЮЦИИ ЦВЕТОВ РАДУГИ
Периодический
закон эволюции цветов радуги может быть
записан в виде следующего монадного
уравнения
 В
данном семействе начальная и конечная
триады являются зеркальными отпечатками
друг друга (подробнее).
Это уравнение свидетельствует о том, что
конечная триада может
служить основой для порождения новой гаммы
цветов радуги, но уже в другом "измерении".
Какими свойствами будет обладать это
измерение?
В
данном семействе начальная и конечная
триады являются зеркальными отпечатками
друг друга (подробнее).
Это уравнение свидетельствует о том, что
конечная триада может
служить основой для порождения новой гаммы
цветов радуги, но уже в другом "измерении".
Какими свойствами будет обладать это
измерение?
7. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭВОЛЮЦИИ МУЗЫКАЛЬНОЙ ГАММЫ

Ниже
(подробнее)
при анализе свойств частиц музыкальной
гаммы рассмотрены правила порождения
других нот хроматической гаммы.
8. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭВОЛЮЦИИ ТИПОВ ЛИЧНОСТИ
В соционике для типов личности
приняты обозначения, которые полностью
совпадают с обозначениями, принятых для
монадных кварков. Поэтому, не углубляясь в
физических смысл символов, можно сразу
сазать, что описанные в п. 2 настоящей
страницы класификация монадных частиц
полностью применима к анализу
существующих в соционике классификаций
типов личности. Более того, Периодические
законы эволюции монадных семейств
характеризуют еще один класс типов
личностей, который в соционике в явном виде
пока не рассматривается, хотя он имеет
чрезвычайно важное и самостоятельное
значение. Это класс триплетных семейств
типов личностей.
9.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ ЭВОЛЮЦИИ СОЦИАЛЬНЫХ СИСТЕМ
В общественных системах каждое устойчивое
двойственное отношение, трансформируемое в
монаде, может породить соответствующее монадное семейство. Однако любое из них
вписывается в рамки Единого Универсального
закона, в рамки эволюции монадных семейств,
рассмотренных выше.
На страницах данного сайта читатель может
найти много примеров Периодических
законов эволюции тех или иных
двойственных социальных отношений. В
частности, на сайте подробно обоснованы следующий
Периодический закон социальных систем: "Свойства
любой социальной системы находится в
периодической зависимости от свойств
самодостаточного двойственного отношения (монады),
определяющего сущность данной социальной
системы».
В
рамках этого закона обоснованы
Периодические законы и принципы:
-
Принципы
нового социального мышления, (принципы
высшей демократии),
-
Периодический
закон эволюции социальных систем,
-
Периодический
закон Всеобщего Управления и Контроля
Качеством социальных отношений,…
-
Периодический закон
удовлетворения социальных нужд,
-
…
-
10.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ ЭВОЛЮЦИИ СОЗНАНИЯ
Периодические законы сознания:
"Свойства
любого духовного объекта находятся в
периодической зависимости от свойств
самодостаточного двойственного отношения (монады),
характеризующего сущность этого объекта (подсознание
и сознание)».
Обоснованы
следующие Периодические законы:
-
Периодический
закон эволюции сознания человека,
-
Периодический
закон эволюции сознания общества,
-
Периодический
закон эволюции Высшего разума,
….
В
основе этих законов также лежат
Периодические законы эволюции монадных
семейств, рассмотренных выше, и порожденных
Единым Универсальным Законом эволюции
живой и неживой материи. Эти законы имеют
особо актуальное значение. Они показывают
путь выхода человечества из клоаки "бессознательного",
открытую З.Фрейдом и К.Юнгом и освященную
темными силами, стремящимися не допустить
эволюцию Сознания к его совершенным формам,
в соответствии с Универсальным законом.
11. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ
ЭВОЛЮЦИИ ЭКОНОМИЧЕСКИХ СИСТЕМ
На страницах сайта обосновано достаточно
много новых, неизвестных ранее,
Периодических законов эволюции
двойственных экономических отношений.
Знание этих законов будет полезно не
только экономистам, но и олигархам всех
мастей, т.к. позволит предоставить им выбор.
Или они, проявляя разум, будут
руководствоваться закономерностями
Единого закона, либо Единый закон, создав
соответстующую "негативную" спираль,
погубит человечество, а вместе с ним и
олигархов. Все возрастающая конкуренция, в
соответствии с Единым законом, приводит
ко все большей интеграции
потребителя и производителя. Попытка
решить эту проблему за счет
монополистической интеграции капитала и
производства в обозримом будущем не будет
иметь успеха.
На
страницах сайта обоснован следующий Периодический
закон экономических систем:
"Свойства любой
экономической системы находятся в
периодической зависимости от свойств
самодостаточного двойственного отношения (монады),
определяющего сущность данной
экономической системы".
В рамках этого закона рассмотрены
следующие законы и принципы:
-
Принципы
нового экономического мышления,
-
Периодический
закон эволюции финансово-хозяйственной
деятельности предприятий,
-
Периодический
закон Всеобщего Управления и Контроля
Качества,
-
Периодические
законы маркетинга,
-
...
12. ПЕРИОДИЧЕСКИЕ ЗАКОНЫ ЭВОЛЮЦИИ ГЕНЕТИЧЕСКОГО
КОДА
Описанные выше свойства монадных семейств
и частиц отражают фундаментальные подходы к познанию
реальности и многоуровневость вселенского
генетического кода. На страницах
сайта достаточно подробно рассмотрены
основные свойства дуплетных и
триплетных генетических кодов, анализ
свойств которых приводит к единственно
верному выводу о том, что принципы и
правила порождения генетических частиц
совпадают с принципами и правилами
порождения монадных частиц.
13.
ПЕРИОДИЧЕСКИЕ ЗАКОНЫ ЭВОЛЮЦИИ ЕДИНОГО
ПОЛЯ
На
страницах сайта довольно подробно
рассматривается проблема Единого поля.
Периодичность
свойств монадных частиц, правил их
порождения позволяют сделать вывод, что
свойства Единого Поля, о котором вот уже
много десятилетий дискуссируют физики всех
мастей, являются общими со свойствами
соответствующих монадных частиц. В
соответствии с гипотезой, изложенной на
сайте свойства квантованных частиц Единого
поля совпадает со свойствами
элементарных частиц, для которых то или
иное поле является внешней средой, которое
их, видимо. и порождает. Ограниченность
типов семейств элементарных частиц, в том
числе и их семейств, позволяет говорить об
эволюционных и многоуровневых принципов
порождения "частиц" Единого поля.
РЕЗЮМЕ
1. Рассмотренные выше правила порождения
монадных частиц из монадных кварков
позволяют сделать вывод о том, что
существуют всего только два типа монадных
семейств -дуальные и триплетные
семейства. Других семейств в природе не
существует. Поэтому свойства этих монадных
семейств и их частиц лежат в основе всех
Периодических законов в Природе, в основе
Единого Универсального закона Вселенной.
2.
Единые правила порождения монадных
частиц (и семейств) имеют чрезвычайно
важное значение для всех без исключения
отраслей наук, т.к. позволят осуществить научные прорывы во
многих сферах знания. В природе нет
других принципов классификации монадных
частиц и их семейств, нет других правил их
порождения. Эти свойства, правила и
принципы будут
являться едиными для любой Периодической
системы, независимо от ее природы.
4.
Принципы и правила порождения монадных
семейств и частиц непосредственно
характеризуют суть и сущность проявления
Единого Универсального Закона применительно к
любой системе, независимо от ее природы,
включая законы эволюции Сознания, Разума и
Высшего разума, демонстрируя единство
Материи и Духа.
Дискретность (квантованность) монадных частиц неизбежно приводит к
выводу, что Единый Универсальный закон
порождает Единую квантовую физику
Материи и физику Духа (сознания).
e-mail:
С
благодарностью приму все ваши замечания, предложения,
с признательностью
отвечу на ваши вопросы
|




 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©

 ,
,