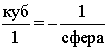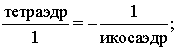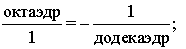5.4.2.1.1.Монадные формы

 

Главная Вверх 
          "Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего".   (Высший разум, ченнелинг).   
                                                                            М.И. Беляев, 2015г,?
 
 МОНАДНЫЕ ФОРМЫ
 
   1. ОБ ЭВОЛЮЦИИ МОНАДНЫХ ФОРМ
         Принципы эволюции двойственных отношений и правила обхода монадных форм "по кресту", порождающих новую совершенную монадную  форму, новый, боле сложный функциональный крест, позволяют говорить и о подобии монадных форм. Уникальность креста освящена всеми мировыми религиями и древними учениями. 
         Любой  "крест" символизирует два принципиально разных типа   эволюции монады. Он характеризует главное свойство эволюции монады. При переходе к формированию двойственной "перекладины" креста, каждая из которых характеризует новое "измерение" эволюции монады, направление обхода креста изменяется на 900. Единый принцип "обхода по кресту" позволяет  по индукции строить более сложные тетраэдры и звездные тетраэдры, например, на ее основе построить новый  "крест", составленный из двух пар  тетраэдров <L1,D1> и <L2,D2>. 
Рис. 1            
Так, например, сопоставляя, например, эволюцию по "перекладинам креста" (<L1,D1>  и <L2,D2>) с эволюцией соответствующих пар "материя-материя" и "дух-дух", мы придем к выводу, что эволюция  пар (звездные тетраэдры <D2,L1> и <D1,L2>) будет характеризовать процессы трансформации пар типа "материя-дух" и "дух-материя". В самом общем случае эволюцию монады можно представить в виде следующей схемы (рис.2-4).
                   Рис.2                                                   Рис.3                                              Рис.4
        Рис. 2 отражает формирование L-тетраэдра из "первичной" монады. Данную структуру  будем далее называть монадным тетраэдром (или L-монадой). На рис. 3  L-тетраэдр формируется уже из монады (L+D-монады). Каждая "перекладина креста"  представляет собой  уже  звездный  U-тетраэдр, каждая вершина которого является L-монадой. Такую фигуру будем назвать монадным крестом.    Рис. 4 характеризует процесс формирования  звездной L-  монады, которую  будем называть звездным крестом. Итак, мы имеем всего 4 базисных фигуры:
  • 1. исходная монада (L-монада) ,
  • 2. Монадный тетраэдр (L-тетраэдр),
  • 3.  Монадный крест (L+D-монада),
  • 4.Звездный крест (L+D-тетраэдр).
            Таким образом, эти 4 фигуры характеризуют  структуру оболочек Единого Периодического закона, его многоуровневость, а  звездный крест отражает самую сложную совершенную форму эволюции монады.  
             Данный    "крест", составленный из звездных тетраэдров,  является не просто символом религий. Он характеризует основные свойства Периодического закона, природу периодичности его свойств и  лежит в основе информационно-генетического кода Вселенной. В процессе первого "крещения" 4 тетраэдра порождают 4 звездных тетраэдра
<D1,L1>,<L1,D2>,<D2,L2>,<,L2,D2>
          Будем считать, что данные звездные тетраэдры характеризуют первые четыре периода эволюции Единого закона (первые 4 оболочки Единой Периодической таблицы).  При этом после завершения круга эволюции мы снова окажемся  в начальной точке, но сдвинутой  по фазе на 180 градусов, т.е.  движение по "перекладинам креста" является полным аналогом ленты Мёбиуса. Необходимо сделать еще один дополнительный оборот, чтобы вернуться в исходное положение. 
<D*1,L*1>,<L*1,D*2>,<D*2,L*2>,<,L*2,D*2>
        Эти оболочки характеризуют последующие четыре периода эволюции Единого закона. Будем их назвать гипероболочками 5-8 Единого закона. Они сдвинуты от соответствующих им оболочек  на 1800. Таким образом, полный цикл эволюции звездной монады формированием 4-х звездных семейств и четырех звездных гиперсемейств (рис. 5). 
Рис. 5
        Отметим, что гипероболочки сдвинуты по фазе относительно оболочек на 1800. Поэтому, по аналогии с оболочками, с учетом фазового сдвига, мы будем иметь следующие гипероболочки:
  • 2. Гипермонадный тетраэдр (D-тетраэдр),
  • 3.  Гипермонадный крест (D+L-монада),
  • 4. Гиперзвездный крест (D+L-тетраэдр).
  • 8. Совершенная  монада (D-монада) ,
        На данном рисунке видно, что в центре гексады находится единственный элемент -двойственная монада (D+Lмонада), интегрированная в звездный тетраэдр (?Я есмь альфа и омега. Начало и Конец. Первый и Последний?) и что в процессе эволюции  исходной монады, во всех  ее вершинах происходит формирование "креста" (тетраэдра). Родственные  дуальные "семейства"   тетраэдров  располагаются в противолежащих вершинах (<1,8>,<2,5>,<3,6>,<4,7>).  При этом в центре гексады будет находиться  монада (две исходные "частицы"), в вершине 2 будет находиться 4 исходных "частицы", составленные из двух исходных, т.е. 8 исходных "частиц", в вершине 3 этих частиц будет уже  16, а вершина 4 будет содержать уже 32  исходных "частицы". Нетрудно понять, что соответствующие гипероболочки будут содержать  такое же число исходных "частиц".  Однако, кроме дуальных семейств, порождаемых той или иной монадой, могут существвовать и триплетные монадные семейства. Свойства монадных семейств и сойства их частиц будут подробно описаны ниже.
        Таким образом, анализ эволюции звездных показывает, что оболочки и гипероболочки Единого Периодического закона напоминает  структуру  Периодической  таблицы химических элементов, т.е.
<вершины<1,8>,<2,5>,<3,6>,<4,7>>=<<2, 2>,<8, 8>,<16, 16>,<32, 32>>
       Отличие заключается в  третьем члене - вместо <16,16> в Периодической таблице используется соотношение <18,18>.  Анализ вышеприведенной структуры оболочек Единого закона позволяет сделать предварительный вывод о том, что данная структура характеризует закон эволюции совершенных монадных форм. Нетрудно заметить, что подобная  последовательность характеризует бинарный ряд. Такая бинарная последовательность может характеризовать  структуру оболочек монадной формы. Наличие внутри "креста" двух противоположных  (ортогональтных) измерений, позваляет предполагать о  существовании еще одного закона - закона эволюции подоболочек. Ниже будет показано,  что любая монада в процессе своей эволюции по той или иной "перекладине"  креста строит свои отношения с соседними вершинами в соответствии с алгоритмом ряда Фибоначчи
<1:1:2:3:5:8>, 
порождающего золотую пропорцию, т.е. подоболочки монадной формы имеют следующую структуру:
<1:3:5:...>. 
        И снова мы замечаем сходство со структурой подоболочек химических элементов, но с разницей уже в четвертом члене. В Периодической таблице самая сложная подоболочка характеризуется числом 7, а в ряде  Фибоначчи он равен 8.  Таким образом, оболочки и подоболочки монадных форм  формируются по разным законам.  Эти законы как бы характеризуют функциональные свойства целостного креста и его перекладин.  Поэтому  "крест" символизирует  также и процессы взаимопревращения монадных  форм  друг в друга (например, монада  "материя-дух). 
               Если теперь учесть, что число 32 в восьмеричной системе счисления равно 40, то уместно вспомнить следующую храмовую исповедь, которая произносилась в Комнате Маата в Египетском  Храме Инициаций (Маат - это "Истина") и в которой имеется вначале упоминание о двух  и сорока законах: "Почтение Тебе,...,Властелин Истины, ... и я пришел сюда, чтобы осознать Твои Законы. ...и Твои два  и еще сорок законов существуют с Тобой..".   Этот фрагмент исповеди может свидетельствовать о том, что древним была извстна восьмеричная система счисления. Сорок - это максимальное число измерений собственного пространства монады (ее самой большой подоболочки), а число два  характеризуют два главных монадных семейства, отражающих специфику эволюции монадных  отношений. Следовательно,   это позволяет сделать удивительно простой и естественный вывод о том, что Единый Универсальный закон Вселенной открыт заново, а восьмеричная система счисления также была известна древним. Он был просто утерян  в седой древности, а его проявления доводились но нашей цивилизации не только фрагментарно, но, нередко, и с искажениями.  Видимо, для  этого наступила пора:  
        "Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего".   
                                                     (Высший разум, ченнелинг).   
 
        2. ОСНОВНЫЕ МОНАДНЫЕ ФОРМЫ И ИХ СВОЙСТВА 
         Рассмотрнные выше принципы эволюции двойственных отношений и их основные свойства, позволяют говорить о  некотором иерархическом пространстве монадных форм, каждая из которых характеризуется  индивидуальными свойствами и индивидуальными наборами собственных значений ([1],[2]), порождающих соответствующую группу симметрии форм этого пространства. 
     Какую монадную форму имеют   эти иерархические пространства? Как происходит эволюция этих монадных форм? Если крест порождает закон эволюции совершенных монадных форм, из которых происходит   формирование монадных оболочек. При этом о эволюция любой  монадной формы,  от одной ее совершнной формы  до другой, осуществляется по Единому  закону. 
         Поэтому  число возможных монадных форм будет  ограниченным и замкнутым, обеспечивая тем самым возможность инвариантных переходов из одного собственного пространства (монадной оболочки, формы) в другое. Каждый раз, когда в монаде  меняется какое-либо собственное значение, то двойственное отношение трансформируется в новое устойчивое состояние и, соответственно, приобретает новую монадную форму.  Периодическое изменение монадных форм в процессе их эволюции сопровождается и периодичностью повторения этих  форм.  В плоских монадных формах  схема эволюции   будет проявляться в переходе к следующей вершине гексады ( по часовой стрелке, или против). В монадных кристалах  такие переходы будут осуществляться по ребрам  соответствующих пространственных монадных форм, в строго упорядоченной последовательности.
        Рассмотрим вначале некоторые основные свойства монадных форм, существующих в природе.   Существует всего пять уникальных форм, имеющих первостепенное значение. Они называются Платановыми телами. Любое Платоново тело имеет некоторые особые характеристики. Во-первых, все грани такого тела равны по размеру. Во-вторых, ребра Платонова тела ? одной длины. В-третьих, внутренние углы между его смежными гранями равны. И в-четвертых, будучи вписанным в сферу, Платоново тело каждой своей вершиной касается поверхности этой сферы.
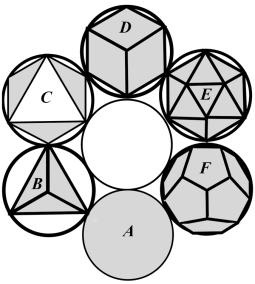        Рис. 6
             Есть только четыре формы помимо куба (D), имеющие все эти характеристики. Второе тело (В) ? это тетраэдр (тетра означает ?четыре?), имеющий четыре грани в виде равносторонних треугольников и четыре вершины. Еще одно тело (C) ? это октаэдр (окта означает ?восемь?), восемь граней которого ? это равносторонние треугольники одинакового размера. Октаэдр содержит 6 вершин. Куб имеет 6 граней и восемь вершин.   Два других Платоновых тела несколько сложнее. Одно (E) называется икосаэдр, что означает ?имеющий 20 граней?, представленных равносторонними треугольниками.  Икосаэдр имеет 12 вершин. Другое (F) называется додекаэдр (додека ? это ?двенадцать?). Его гранями являются 12 правильных пятиугольников. Додекаэдр имеет двадцать вершин. Эти тела обладают замечательными свойствами быть вписанными все всего в две фигуры - сферу и куб. Подобная взаимосвязь с Платоновыми телами прослеживается во всех сферах. Так, например, системe орбит планет солнечной системы можно представить в виде вложенных друг в друга Платоновых тел, вписанных в соответствующие сферы, которые и определяют радиусы орбит соответствующих  планет солнечной системы.        
        Фаза А (рис. 6) характеризует начало эволюции монадной формы.  А потому эта форма является как бы самой простой (сферой). Затем рождается тетраэдр, и т.д.
   Куб,  расположен в этой гексаде напротив сферы и потому он  обладает сходными свойствами.
                                                                         
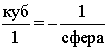          Тогда  свойствами,  сходными с тетраэдром должны обладать монадная форма, расположенная в гексаде напротив тетраэдра. Это  икосаэдр.
                                                                 
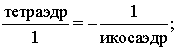Формы додекаэдра должны быть ?родственны? октаэдру.
                                                                
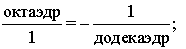         И, наконец, последняя форма снова становится сферой. Последняя становится  первой!
    Кроме того, в гексаде должна наблюдаться  преемственность эволюции  двух соседних Платоновых тел. И, действительно, октаэдр и куб, икосаэдр и додекаэдр взаимны. Если у одного из этих многогранников соединить отрезками прямых  центры граней, имеющих общее ребро, то получится другой многогранник. 
Но наиболее ярко эта взаимность проявляться в случае, когда отношения между соседними кристаллами мы выразим через отношение "число вершин/число граней".
                                                      
           Видите, эти взаимоотношения формируются весами монады (Весы монады).
 В этих свойствах кроется их эволюционное происхождение друг от друга. В  Платоновой  гексаде  можно выделить две триады: ?сфера-октаэдр-икосаэдр? и ?тетраэдр-куб-додекаэдр?, наделяющие соседние вершины собственных  триад свойствами взаимности.               
    Эти фигуры обладают еще одним замечательным качеством. Они связаны крепкими узами с рядом Фибоначчи -<1:1:2:3:5:8:13:21:...>, в котором каждый последующий член равен сумме двух предыдущих.
     Вычислим  разности между членами ряда Фиббоначи и числом вершин в Платоновых телах :
 
 
 
 
 
 
 
 
 
 
 
 
 
 
                                                            2=2-А=2-2=0 (нулевой "заряд"),
                                                            3=3-В=3-4=-1 (отрицательный "заряд"),
                                                           4=5-С=5-6=-1 (отрицательный "заряд"),
                                                           5=8-D=8-8=0 (нулевой "заряд"),
                                                           6=13-Е=13-12=1 (положительный "заряд"),
                                                           7=21-F=21-20=1 (положительный "заряд"),
                                                                                      Рис. 7
     т.е. "монадные заряды" Платоновых тел отражают несоответствие идеальных форм от ряда Фибоначи. 
    Ниже, при обосновании Единого Периодического закона элементарных частиц, мы непосредственно увидим, что элементарные частицы, свойства которой определяются соответствующими вершинами монадной формы, имеют заряды, соответствующие  монадным. Но, поскольку ряд Фибоначи порождает "золотую пропорцию", ответственную за рождение гармонии всего сущего, то и Платоновы тела также будут характеризовать свойства всех материальных структур. Так,  атомы всегда соотносятся с пятью Платоновыми телами. Даже если  разбирать  на части очень сложную молекулу, в ней можно найти  более простые формы, и они всегда могут быть прослежены до одного из пяти Платоновых тел ? независимо от того, какова ее структура. Не имеет значения, что это ? металл, кристалл или что-то еще, ? структура всегда восходит к одной из пяти первоначальных форм.
         Однако, полагая, что начиная с  куба, Платоновы тела могут формировать ВЕЛИКИЕ ПРЕДЕЛЫ (Великий Предел), то становится ясным, что додекаэдр и икосаэдр, отражая взаимодополнительное соответствие между число граней и числом вершин, характеризуемых числами 12 и 20, фактически выражают собой соотношения 13 и 21 ряда Фибоначчи.
     Посмотрите, как происходит нормирование ряда Фибоначчи.
                                                       1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...
                                                                               12, 20, .....
                                                                                 1,   1,   2,   3,   5,   8,   13, ...
    Первая строка отражает "нормальный"  алгоритм формирования ряда Фибоначчи.
   Вторая строка начинается с икосаэдра, в котором 13 вершина оказалась центром структуры, отражая свойства ВЕЛИКОГО ПРЕДЕЛА. Аналогичный ВЕЛИКИЙ ПРЕДЕЛ имеется и у додекаэдра.
    Эти два кристалла порождают новое измерение - нормированную монаду "икосаэдр-додекаэдр", которая и начинает формировать новый виток ряда Фибоначчи (третья строка).
         Следовательно, мы приходим к выводу, что число используемых природой первозданных монадных форм является ограниченным и замкнутым.  К такому же выводу пришел еще много веков назад Платон, который считал, что сложные частицы элементов имеют форму многогранников, при дроблении эти многогранники дают треугольники, которые и являются  истинными  элементами мира.  Достигнув самой совершенной формы, природа берет эту форму в качестве элементарной и начинает строить следующие формы, используя последние в качестве ?единичных? элементов. Поэтому все высшие формы неорганических, органических, биологических и полевых форм материи обязательно должны будут связаны с более простыми монадными кристаллами. Из этих форм должны строиться и самые сложные - высшие формы Высшего разума. И эти свойства монадных кристаллов должны проявляться на всех уровнях иерархии: в структуре элементарных частиц, в структуре Периодической системы элементарных частиц, в структуре атомов, в структуре Периодической системы химических элементов, и т.д. Так, в химических элементах, все подоболочки и оболочки могут быть представлены в форме монадных кристаллов. Естественно, что внутренняя структура атомов химических элементов должна отражаться в структуре кристаллов и  клетках живых организмов.
         ?Любая форма есть производное  одного из пяти Платоновых тел. Без исключений. И не имеет значения, какова структура кристалла, она всегда основана на одном из Платоновых тел...? [3].
        Важное место среди всех этих структур занимает куб. Оказывается, что различные кристаллические структуры, состоящие из атомов, могут быть приведены к структуре куба. Может быть, поэтому куб является даже  более важным, чем другие многогранники.   Действительно, куб отличается от других Платоновых тел одной особенностью, которой нет у других, кроме сферы. Как куб, так и сфера могут  вмещать в себя четыре других Платоновых тела и друг друга симметричным образом, охватывая их своей поверхностью, если тела имеют подходящие размеры.
     Куб ? это единственное Платоново тело с этой характерной особенностью: вы можете взять сферу, поместить ее внутрь куба и она будет касаться его шести граней точно и симметрично. Такая взаимосвязь  материальных тел с Платоновыми телами позволяет высказать гипотезу о непосредственной связи этих многогранников с монадной гексадой. Кроме того, куб может рассматриваться как другая фигура-звездный тетраэдр, с которым далее мы встетимся неоднократно и которому, собственно материя обязана рождением двойной спирали ДНК.
                          
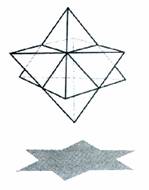
                                                                             Рис. 8
   Два взаимодополнительных тетраэдра, как будет показано ниже, составляют основу кода ДНК (подробнее). Когда в одном тетраэдре возникает восходящая спираль ("вихрь"), то в другом -нисходящая ("воронка"). Фигуры, изображенные на рис. 3,  будут далее  встречаться  практически везде, в той или иной форме.  Это самые  фундаментальные монадные формы. Симметрия этих форм и их проекции на плоскоть хорошо иллюстрирует рис.9. 
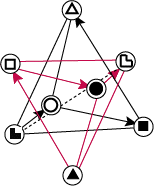рис. 9
Все фигуры, изображенные на рис. 8 и 9, отображают разные грани (проекции) одной и той же монадной формы. На рис. 10 приведена еще одна форма, показывающая взаимосвязь между тетраэдрами и кубом
рис. 10
     Рассмотрим, как и в какой последовательности происходит заполнение монадной формы. Это, как мы убедимся впоследствии, действительно, типовая форма-бланк, графы которой заполняются в строго определенной последовательности.  Вначале, по ребрам куба,  заполняются первые 3 "графы", лежащие на одной плоскости. Затем происходит переход к другому измерению (вершина 4). От вершины 4 происходит переход через "пустоту" к вершине 5. Далее в этой плоскости к вершине 5 пристраиваются  вершины 6 и 7, после чего происходит переход в новое измерение (вершина 8). В результате такого заполнения, формируются 4 оси симметрии, образованными парами вершин 
<1-8; 2-5; 3-6; 4-7>.  
     Такая последовательность заполнения типового монадного бланка является не случайным совпадением с последовательность образования Платоновых тел.
  Развитие форм жизни также происходит через Платоновы тела. На первом этапе зарождения жизни из одной клетки, путем ее деления пополам, получается  две клетки.  На следующем этане клетки вновь делятся, образуя из двух четыре, как в бинарной последовательности ? 1, 2, 4, 8, 16 и т. д. Первые четыре клетки  образуют тетраэдр ? одно из Платоновых тел. Далее клетки делятся до восьми, образуя один тетраэдр, направленный кверху, и один тетраэдр, направленный книзу, и мы получаем звездный тетраэдр.  Все до единой формы жизни  должны пройти эту стадию.  Первые восемь клеток образуют звездный тетраэдр, или куб, в зависимости от того, как  на него смотреть.
        После разделения на восемь клеток происходит деление на 16 клеток, в результате чего образуется другой куб, или звездный тетраэдр. Это последний раз, когда все симметрично.... Это тоже одна  высших монадных форм. Оказывается, что  далее необходимо 18 клеток для того, чтобы была симметрия... Это одна из самых сложных симметричных монадных форм.
         ?При следующем делении получается на 32 клетки больше, но становится еще хуже.... Начинается превращение в комковое образование. Мы превращаемся в сферу, начиная с 32 клетки. Но... далее комок растягивается и его нутро начинает выворачиваться наружу, становясь пустотелым шаром. Дойдя до этой стадии, он становится идеальной пустотелой сферой. Затем северный полюс начинает опускаться через все пространство вовнутрь, двигаясь вниз к южному полюсу, а южный полюс поднимается через это пространство, встречаясь с северным полюсом.... Потом пустотелая сфера, на стадии 512 клеток,  становится тором -сферическим тором,... Каждая известная форма жизни проходит через стадию тора?.  Так пишет об эволюции живых клеток Друнвало Мелхиседек [3].
        Таким образом,  при переходе в новое состояние структура и  симметрия монады  изменяется. Но изменяется не произвольно, а в соответствии с уже рассмотренными выше формами. Как бы ни был сложен  мир ?кварковых? кристаллов, он складывается и эволюцирует по вполне определенным правилам, периодически повторяясь,  видоизменяясь  и преобразовываясь друг  в друга на всех уровнях иерархии,  руководствуясь Единым Периодическим Законом, отражаемым соответствующими  монадными формами.  При этом на разных уровнях иерархии   кварковые свойства триад и гексад вырождаются в  ?многолепестковую? систему вложенных друг в друга  и  сдвинутых друг относительно друга на определенный угол триад и гексад.  Например, именно такую структуру имеет минерал берилла.
                                                                                                      Рис. 11
            Она состоит из 4-х больших   фрагмента, каждый из которых составлен из 4-х триад (или из двух противоположных гексад). В центре кристалла видны еще два  кристалла (икосаэдра). Эти икосаэдры соединяют между собой большие  фрагменты таким образом, что они оказываются  закручены друг относительно друга в спираль. Каждый  большой фрагмент сдвинут относительно друг друга на угол . В результате 1-й и 4-й фрагмент оказываются в ?противофазе?, т.е. зеркально противоположны  друг другу.
           Таким образом, эволюция монадных форм происходит не случайным образом и к этой  эволюции причастен самым тесным образом алгоритм Фибоначчи.
   
     
e-mail:
    С благодарностью приму все ваши замечания, предложения,
с признательностью отвечу на ваши вопросы
    ? Беляев М.И., "МИЛОГИЯ", 2015г.
 Опубликован: 26/10/2013г., обновлен: 02 октября 2014.
           Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать  о всех замеченных ошибках, некорректных формулировках.
         Книги "Основы милогии", "Милогия" могут  быть высланы в Ваш адрес наложенным платежом,
  

????? ?????

rss
Карта