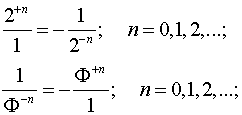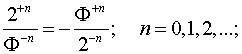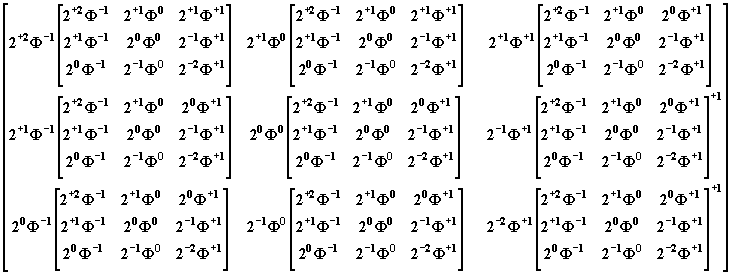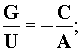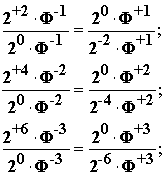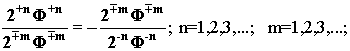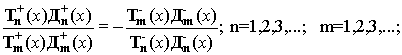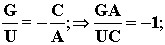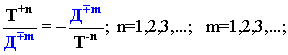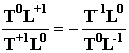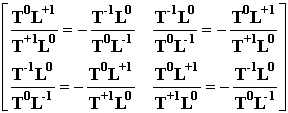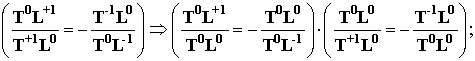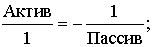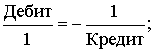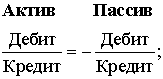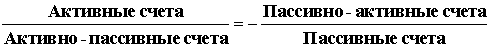Русская матрица-2

Русская матрица-2

"Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг).

М.И. Беляев, 2015г,©

Часть 2. ЗОЛОТОЙ ГИПЕРКУБ РУССКОЙ МАТРИЦЫ

1. ЗОЛОТОЙ ГИПЕРКУБ РУССКОЙ МАТРИЦЫ

1.1. ПРОИЗВОДЯЩИЕ ФУНКЦИИ РУССКОЙ МАТРИЦЫ

На странице "Преемственность" были обоснованы свойства производящих функций, отражающих правила инвариантной преемственности.

Из математики известно, что всякий раз, когда нам нужно получить информацию о последовательности чисел

<a_n> = < a₀, a₁, a₂, a₃, ...>

мы можем образовать бесконечную сумму по степеням параметра “х”

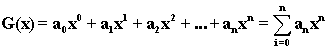
т. е. производящую функцию для числовой последовательности (1). Если эта последовательность определена интуитивно, т. е. если аn определяется по а₁, а₂, а₃,..., то это дает важные преимущества при исследовании.

Многие поколения математиков в своих исследованиях использовали производящие функции. Важное значение при использовании производящих функций имеет вопрос о сходимости бесконечной суммы. Однако, с другой стороны, работая с производящими функциями, часто можно не беспокоиться о сходимости ряда, поскольку мы лишь исследуем возможные подходы к решению некоторой задачи. Когда мы найдем решение каким-либо способом, как бы не строг он ни был, можно всегда независимым способом убедиться в верности этого решения. Производящие функции очень широко используются в математике, т. к. являются мощным оружием при решении практических задач, связанных, например, с перечислением, распределением и разбиением множеств объектов различной природы.

Отметим, что в некоторых разделах математики, например, в комбинаторике, переменная х никак не определена и считается просто абстрактным символом, роль которого сводится к тому, чтобы различать элементы числовых последовательностей. При этом различные преобразования таких последовательностей заменяются соответствующими операциями над производящими функциями.

Используя производящие функции

....+2⁵+2⁴+2³+2²+2¹+2⁰+2^-1+2^-2+2^-3+2^-4+2^-5+.....

....+Ф⁵+Ф⁴+Ф³+Ф^Ф+Ф¹+Ф⁰+Ф^-1+Ф^-2+Ф^-3+Ф^-4+Ф^-5+.....

мы имеем возможность записать в общем виде Русскую матрицу в виде произведений 2^±n Ф^±^m.

В	2⁸	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰	A^*
2⁸	2⁺⁸Ф^-4	2⁺⁷Ф^-3	2⁺⁶Ф^-2	2⁺⁵Ф^-1	2⁺⁴Ф⁰	2⁺³Ф⁺¹	2⁺²Ф⁺²	2⁺¹Ф⁺³	2⁰Ф⁺⁴	2⁰
2⁷	2⁺⁷Ф^-4	2⁺⁶Ф^-³	2⁺⁵Ф^-2	2⁺⁴Ф^-1	2⁺³Ф⁰	2⁺²Ф⁺¹	2^±nФ⁺²	2⁰Ф⁺³	2^-1Ф⁺⁴	2^-1
2⁶	2⁺⁶Ф^-4	2⁺⁵Ф^-3	2⁴Ф^-2	2⁺³Ф^-1	2⁺²Ф⁰	2⁺¹Ф⁺¹	2⁰Ф⁺²	2^-1Ф⁺³	2^-2Ф⁺⁴	2^-2
2⁵	2⁺⁵Ф^-4	2⁺⁴Ф^-3	2⁺³Ф^-2	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2^-1Ф⁺²	2^-2Ф⁺³	2^-3Ф⁺⁴	2^-3
2⁴	2⁺⁴Ф^-4	2⁺³Ф^-3	2⁺²Ф^-2	2⁺¹Ф^-1	2⁰Ф⁰	2^-1Ф⁺¹	2^-2Ф⁺²	2^-3Ф⁺³	2^-4Ф⁺⁴	2^-4
2³	2⁺³Ф^-4	2⁺²Ф^-3	2⁺¹Ф^-2	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2^-3Ф⁺²	2^-4Ф⁺³	2^-5Ф⁺⁴	2^-5
2²	2⁺²Ф^-4	2⁺¹Ф^-3	2⁰Ф^-2	2^-1Ф^-1	2^-2Ф⁰	2^-3Ф⁺¹	2^-⁴Ф⁺²	2^-5Ф⁺³	2^-6Ф⁺⁴	2^-6
2¹	2⁺¹Ф^-4	2⁰Ф^-3	2^-1Ф^-2	2^-2Ф^-1	2^-3Ф⁰	2^-4Ф⁺¹	2^-5Ф⁺²	2^-6Ф⁺³	2^-7Ф⁺⁴	2^-7
2⁰	2⁰Ф^-4	2^-1Ф^-3	2^-2Ф^-2	2^-3Ф^-1	2^-4Ф⁰	2^-5Ф⁺¹	2^-6Ф⁺²	2^-7Ф⁺³	2^-8Ф⁺⁴	2^-8
A	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	В^*

рис.1

Отметим, что каждый производящий ряд состоит из левой и правой части, которые мы можем записать в форме двумерных взаимодополнительных весов

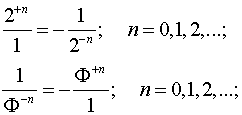из которых можно сформировать 4-х мерные весы

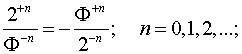Это тождество является базисным, из которого строятся, по образу и подобию, на всех уровнях иерархии многомерные весы Русской матрицы.

В центре Русской матрицы располагается системообразующая матрица-энеаграмма.

Это проекция на плоскость "базисного кубика", в центре которого размещается девятая вершина -Великий Предел этого "кубика" (Единица).

Свойства Русской матрицы дают самое первое представление о том, что в каждой частице Вселенной содержится информация о всей Вселенной. Каждое число Русской матрицы является мировой константой, порождающей, по образу и подобию собственную Русскую матрицу.

Если центр базисной матрицы совместить с любым числом Русской матрицы, то умножив все члены этой матрицы на данное золотое число, то мы получим соответствующий фрагмент Русской матрицы. Продолжая эту матрицу, мы придем к выводу, что каждое число Русской матрицы может порождать, по образу и подобию, всю Русскую матрицу, в явном виде отражая свойства фрактальности.

Рассмотрим базисную матрицу -"кубик", с Великим пределом- девятой вершиной (Единицей-2⁰Ф⁰)

2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹
2⁺¹Ф^-1	2⁰Ф⁰	2^-1Ф⁺¹
2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹

В гиперматрице, приведенной ниже и состоящей из 9 базисных кубиков, каждое золотое число, стоящее в девятой вершине базисного "кубика" является "мировой константой"- творцом собственной Русской матрицы, которая порождается путем умножения собственного золотого числа на каждое число собственной базисной матрицы.

2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹
2⁺¹Ф^-1	2²Ф^-1	2^-1Ф⁺¹	2⁺¹Ф^-1	2⁺¹Ф⁰	2^-1Ф⁺¹	2⁺¹Ф^-1	2⁰Ф⁺¹	2^-1Ф⁺¹
2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹
2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹
2⁺¹Ф^-1	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁺¹Ф^-1	2⁰Ф⁰	2^-1Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2^-1Ф⁺¹
2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹
2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹
2⁺¹Ф^-1	2⁰Ф^-1	2^-1Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁰	2^-1Ф⁺¹	2⁺¹Ф^-1	2^-2Ф⁺¹	2^-1Ф⁺¹
2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹

рис. 2

Процесс получения гиперматрицы можно формально отобразить в следующем виде.

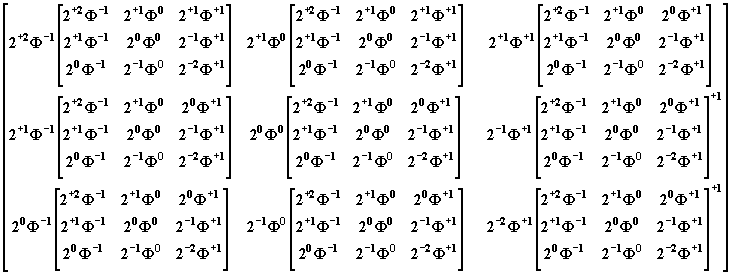рис.3

Видите, в этой матрице каждое число базисной матрицы скалярно умножается на базисную матрицу-"кубик". В результате мы получаем гиперкуб. Если мы выполним умножение и наложим равные золотые числа друг на друга (без суммирования, то мы получим фрагмент Русской матрицы, но уже большей размерности.

2⁴Ф^-2	2⁺³Ф^-1	2⁺²Ф⁰	2⁺¹Ф⁺¹	2⁰Ф⁺²
2⁺³Ф^-2	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2^-1Ф⁺²
2⁺²Ф^-2	2⁺¹Ф^-1	2⁰Ф⁰	2^-1Ф⁺¹	2^-2Ф⁺²
2⁺¹Ф^-2	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2^-3Ф⁺²
2⁰Ф^-2	2^-1Ф^-1	2^-2Ф⁰	2^-3Ф⁺¹	2^-⁴Ф⁺²

В результате мы получили новые мировые константы, которые разворачиваясь по образу и подобию и формируя бесконечномерную собственную Русскую матрицу, тем не менее приформируют к Русской матрице, которая их породила, новые золотые "мировые константы", т.е. процесс формирования Русской матрице происходит как вовнутрь, так и вовне.

На предыдущей странице мы приводили следующую схему эволюции триграмм (Книга перемен), совмещенную с нотами музыкальной гаммы и цветами радуги. На этой схеме эволюции базисного "кубика" отображен также и бинарный ряд, и золотой.

рис.4

Теперь, учитывая, что каждая вершина может порождать, про образу и подобию, собственный "кубик", мы получим следующий гиперкуб.

рис.5

Если теперь каждый базисный кубик развернуть в строку, то мы получим 9 строк и, соответственно, матрицу, размерностью 9х9. Обратите внимание, каждый базисный кубик имеет свой цвет.

Нетрудно осознать, что в результате мы получим матрицу И-Цзин, но размерностью 9х9.

На страницах сайта не однократно рассматривались свойства матрицы И-Цзин.

рис.6-1

Из этого рисунка видно, что матрица И-Цзин порождается умножением вектора "мировых констант" на "базисный кубик", развернутый в строку (или столбец), в зависимости от вектора "мировых констант". И в результате мы получаем удвоенные "кубики" в каждой строке, т.е. вместо триграмм, получаем гексаграммы. Если теперь мы при умножении учтем и Великий предел базисного "кубика", о мы как раз и получим расширенную матрицу И-Цзин, свойства которой неоднократно рассматривались на сайте.

рис.6-2

Видите, в этой матрице очень четко выделен крест Великих пределов "кубиков"

А теперь попытаемся матрицу И-Цзин отобразить через золотые числа Русской матрицы.

Базисный кубик через золотые числа можно переписать в следующем виде

1	2	3	4
2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1
2^-2Ф⁺¹	2^-1Ф⁰	2⁰Ф^-1	2^-1Ф⁺¹
5	6	7	8

Посмотрите, здесь числовая симметрия имеет гораздо более глубокий смысл чем симметрия триграмм в матрице И-Цзин. Разворачивая золотой кубик в строку и осуществляя над этой строкой циклический сдвиг, получаем расширенную гиперматрицу

2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰
2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1
2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰
2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹
2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1
2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹
2^-1Ф⁰	2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1
2^-2Ф⁺¹	2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰
2⁰Ф⁰	2⁺²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2⁺¹Ф^-1	2^-1Ф⁺¹	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹

Нетрудно увидеть, используя свойства симметрии, что главная диагональ этой расширенной матрицы является единичной, т.е. это диагональ Великий пределов расширенной матрицы И-Цзин.

А теперь посмотрите, какая симметрия окружает главную диагональ. Она как "экватор", делит всю матрицу гиперкуба на "северное и южное полушария".

При этом, заметьте, на всех диагоналях и поддиагоналях все золотые числа являются равными, чего нельзя сказать про другую главную диагональ и поддиагонали.

2. РУССКАЯ МАТРИЦА И ЗАКОНЫ РЫНОЧНЫХ ОТНОШЕНИЙ

На странице "О механизмах хозяйствования" и др., были рассмотрены свойства природных рыночных отношений спроса и предложения.

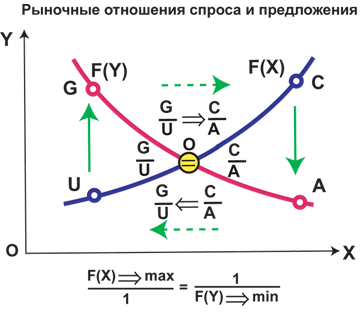рис.7

Этот рисунок отражает в себе не только свойства экономических отношения спроса и предложения. Он несет в себе печать Русской матрицы. Посмотрите. в Русской матрице каждому числу G соответствует ему взаимодополнительное число A, а каждому числу U соответствует взаимодополнительное ему число C.

А теперь можете самостоятельно проверить справедливость тождества на числах Русской матрицы.

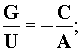Может быть и это случайность, или совпадение? А может быть это тоже бред "мужика от сохи"?

А если вы тот, "кто может читать", то вы можете осознать, по каким законам происходит трансформация янского аспекта в иньский и наоборот, что эта трансформация происходит квантованно и в соответствии с числами Русской матрицы.

Может быть, теперь вы осознаете, что вертикаль ДД^* Русской матрицы играет роль исходной монады, вокруг которой крутятся все числа Русской матрицы, формируя Куб Русской матрицы (рис. 2).

Но, пожалуй, самым замечательным свойством Русской матрицы является то, отношение чисел, стоящих на главных диагоналях матрицы формируют рыночные тождества вида:

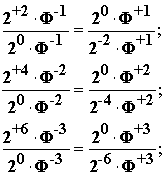Следовательно, в Русской матрице находят свое отражение весы монады (Весы монады)

Выше, рассматривая свойства Русской матрицы, мы получили следующее тождество

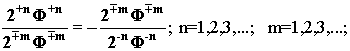характеризующего взаимоотношения между числами Русской матрицы.

Если отождествить капитал-собственность с производящей функцией товара (T_n(x))ºTⁿ, а с капиталом-функцией производящую функцию финансовых (денежных) потоков (Д_n(x))ºДⁿ, то мы можем, по образу и подобию, сформировать Русскую матрицу, определяющую взаимоотношения между потоками капитала.

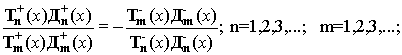Заметим, что здесь все потоки капитала являются нормированными, т.е. имеет место тождество вида (рис. 3-1)

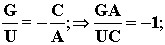Видите, в этих тождествах имеет место нормировка отношений, т.е. т.е. произведение чисел, равноотстоящих от центра матрицы (Единицы) также всегда равны единице.

Нетрудно увидеть, что нормировке подвергаются и отношения чисел, формирующих отношения между главными диагоналями и чисел, стоящими в строках и столбцах матрицы.

Многие экономисты, прочитав эти строки, могут сказать, что автор блефует. Но это совсем не так.

Если, например, с перекладиной монадных весов, отражающего структуру капитала, как отношения между капиталом-собственностью и капиталом-функцией (G/A), тогда вторая перекладина весов будет отражать структуру отношений капитала-функции (U/C). Эти отношения показывают долю капитала-функции, относящуюся к капиталу -собственности, и долю чисто финансовых средств.

В	T^-⁴	T^-3	T^-2	T^-1	T⁰	T¹	T²	T³	T⁴	A^*
	T^-⁴Д⁸	T^-3Д⁷	T^-2Д⁶	T^-1Д⁵	T⁰Д⁴	T¹Д³	T²Д²	T³Д¹	T⁴Д⁰
	T^-⁴Д⁷	T^-3Д⁶	T^-2Д⁵	T^-1Д⁴	T⁰Д³	T¹Д²	T²Д¹	T³Д⁰	T⁴Д^-1
	T^-⁴Д⁶	T^-3Д⁵	T^-2Д⁴	T^-1Д³	T⁰Д²	T¹Д¹	T²Д⁰	T³Д^-1	T⁴Д^-2
	T^-⁴Д⁵	T^-3Д⁴	T^-2Д³	T^-1Д²	T⁰Д¹	T¹Д⁰	T²Д^-1	T³Д^-2	T⁴Д^-3
С	T^-⁴Д⁴	T^-3Д³	T^-2Д²	T^-1Д¹	T⁰Д⁰	T¹Д^-1	T²Д^-2	T³Д^-3	T⁴Д^-4	С^*
	T^-⁴Д³	T^-3Д²	T^-2Д¹	T^-1Д⁰	T⁰Д^-1	T¹Д^-2	T²Д^-3	T³Д^-4	T⁴Д^-5
	T^-⁴Д²	T^-3Д¹	T^-2Д⁰	T^-1Д^-1	T⁰Д^-2	T¹Д^-3	T²Д^-4	T³Д^-5	T⁴Д^-6
	T^-⁴Д¹	T^-3Д⁰	T^-2Д^-1	T^-1Д^-2	T⁰Д^-3	T¹Д^-4	T²Д^-5	T³Д^-6	T⁴Д^-7
	T^-⁴Д⁰	T^-3Д^-1	T^-2Д^-2	T^-1Д^-3	T⁰Д^-4	T¹Д^-5	T²Д^-6	T³Д^-7	T⁴Д^-8
A	T^-⁴	T^-3	T^-2Д^-³	T^-1	T⁰	T¹	T²	T³	T⁴	В^*

Полученную таким образом матрицу будем называть Русской экономической матрицей.

Она отражает новое экономическое мышление. Пусть мы имеем монадное тождество

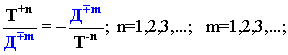В этом тождестве главная диагональ матрицы может смещаться вверх или вниз, за счет манипуляций с финансовыми потоками. Если эти манипуляции исключить, то мы тем самым обуздаем, например, такие негативные явления, как инфляцию (Единое экономическое учение).

В Едином экономическом учении прибыль не самоцель производства товаров. Если один товар оказывается ценнее другого, то и объем производства этого товара будет соответственно увеличен. Другими словами та же самая прибыль будет получена за счет увеличения производства и оборота капитала, но не за счет спекулятивного перераспределения капитала-функции.

От этой матрицы также веет мистикой. Красная клетка с числом "Т^-2Д^-3", по образу и подобию системы эволюции размерностей физических величин (Эволюция размерности), навевает мысль о том, что и система "товарно-денежных отношений" в современной цивилизации также соответствует этой мировой константе. Из этой мировой константы можно сделать вывод о том, что в современной цивилизации преобладают процессы "производства" денег, но не товаров.

Не слишком ли много всевозможных случайностей и совпадений?

3. РУССКАЯ МАТРИЦА ПРОСТРАНСТВА-ВРЕМЕНИ

На странице "Эволюция размерности", в результате системного анализа взаимосвязей размерностей физических величин, была приведена следующая схема эволюции физических величин, в рамках системы МLT.

рис. 8-1

Анализ Русской матрицы показывает, что она состоит из четырех секторов, которые по своей структуре полностью совпадают с вышеприведенной схемой эволюции физичеcких величин пространства "L-T". Ниже приведена Русская матрица пространства-времени, свойства которой были рассмотрены на странице "Матрица " L-T".

В	T^-⁴	T^-3	T^-2	T^-1	T⁰	T¹	T²	T³	T⁴	A^*
	T^-⁴L⁸	T^-3L⁷	T^-2L⁶	T^-1L⁵	T⁰L⁴	T¹L³	T²L²	T³L¹	T⁴L⁰
	T^-⁴L⁷	T^-3L⁶	T^-2L⁵	T^-1L⁴	T⁰L³	T¹L²	T²L¹	T³L⁰	T⁴L^-1
	T^-⁴L⁶	T^-3L⁵	T^-2L⁴	T^-1L³	T⁰L²	T¹L¹	T²L⁰	T³L^-1	T⁴L^-2
	T^-⁴L⁵	T^-3L⁴	T^-2L³	T^-1L²	T⁰L¹	T¹L⁰	T²L^-1	T³L^-2	T⁴L^-3
С	T^-⁴L⁴	T^-3L³	T^-2L²	T^-1L¹	T⁰L⁰	T¹L^-1	T²L^-2	T³L^-3	T⁴L^-4	С^*
	T^-⁴L³	T^-3L²	T^-2L¹	T^-1L⁰	T⁰L^-1	T¹L^-2	T²L^-3	T³L^-4	T⁴L^-5
	T^-⁴L²	T^-3L¹	T^-2L⁰	T^-1L^-1	T⁰L^-2	T¹L^-3	T²L^-4	T³L^-5	T⁴L^-6
	T^-⁴L¹	T^-3L⁰	T^-2L^-1	T^-1L^-2	T⁰L^-3	T¹L^-4	T²L^-5	T³L^-6	T⁴L^-7
	T^-⁴L⁰	T^-3L^-1	T^-2L^-2	T^-1L^-3	T⁰L^-4	T¹L^-5	T²L^-6	T³L^-7	T⁴L^-8
A	T^-⁴	T^-3	T^-2L^-³	T^-1	T⁰	T¹	T²	T³	T⁴	В^*

рис. 8-2

В этой матрице в красной клетке находится базисная размерность (T^-2L^-³) системы MLT.

Перепишем теперь данную матрицу в следующем виде.

T^-5L¹⁰	T^-⁴L⁹	T^-3L⁸	T^-2L⁷	T^-1L⁶	T⁰L⁵	T¹L⁴	T²L³	T³L²	T⁴L¹	T⁵L⁰
T^-5L⁹	T^-⁴L⁸	T^-3L⁷	T^-2L⁶	T^-1L⁵	T⁰L⁴	T¹L³	T²L²	T³L¹	T⁴L⁰	T⁵L^-1
T^-5L⁸	T^-⁴L⁷	T^-3L⁶	T^-2L⁵	T^-1L⁴	T⁰L³	T¹L²	T²L¹	T³L⁰	T⁴L^-1	T⁵L^-2
T^-5L⁷	T^-⁴L⁶	T^-3L⁵	T^-2L⁴	T^-1L³	T⁰L²	T¹L¹	T²L⁰	T³L^-1	T⁴L^-2	T⁵L^-3
T^-5L⁶	T^-⁴L⁵	T^-3L⁴	T^-2L³	T^-1L²	T⁰L¹	T¹L⁰	T²L^-1	T³L^-2	T⁴L^-3	T⁵L^-4
T^-5L⁵	T^-⁴L⁴	T^-3L³	T^-2L²	T^-1L¹	T⁰L⁰	T¹L^-1	T²L^-2	T³L^-3	T⁴L^-4	T⁵L^-5
T^-5L⁴	T^-⁴L³	T^-3L²	T^-2L¹	T^-1L⁰	T⁰L^-1	T¹L^-2	T²L^-3	T³L^-4	T⁴L^-5	T⁵L^-6
T^-⁵L³	T^-⁴L²	T^-3L¹	T^-2L⁰	T^-1L^-1	T⁰L^-2	T¹L^-3	T²L^-4	T³L^-5	T⁴L^-6	T⁵L^-7
T^-5L²	T^-⁴L¹	T^-3L⁰	T^-2L^-1	T^-1L^-2	T⁰L^-3	T¹L^-4	T²L^-5	T³L^-6	T⁴L^-7	T⁵L^-8
T^-⁵L¹	T^-3L⁰	T^-3L^-1	T^-2L^-2	T^-1L^-3	T⁰L^-4	T¹L^-5	T²L^-6	T³L^-7	T⁴L^-8	T⁵L^-⁹
T^-5L⁰	T^-4L^-1	T^-3L^-2	T^-2L^-3	T^-1L^-4	T⁰L^-5	T¹L^-⁶	T²L^-⁷	T³L^-⁸	T⁴L^-⁹	T⁵L^-¹⁰

рис. 8-3

В этой матрице выделены 4 сектора. Диагонали Русской матрицы являются общими для двух смежных секторов. Рассмотрим эволюцию желтых секторов. В соответствии с законами сохранения симметрии мы получим следующую "свастичную" матрицу, составленную из 4-х базисных кубиков.

T^-1L²	T⁰L¹	T¹L⁰	T^-1L²	T⁰L¹	T¹L⁰
T^-1L¹	T⁰L⁰	T¹L^-1	T^-1L¹	T⁰L⁰	T¹L^-1
T^-1L⁰	T⁰L^-1	T¹L^-2	T^-1L⁰	T⁰L^-1	T¹L^-2

T^-1L²	T⁰L¹	T¹L⁰	T^-1L²	T⁰L¹	T¹L⁰
T^-1L¹	T⁰L⁰	T¹L^-1	T^-1L¹	T⁰L⁰	T¹L^-1
T^-1L⁰	T⁰L^-1	T¹L^-2	T^-1L⁰	T⁰L^-1	T¹L^-2

рис. 8-4

Посмотрите, мы получили 4 "свастичных" матрицы, каждая из которых включает в себя две системы физических размерностей (рис. 8-1).

Таким образом, видимо, можно придти к выводу, что система физических размерностей определяет место нашего мироздания в другой, абсолютной для нас вселенной физических размерностей.

Интересно заметить, что мировая константа "T^-2L^-3" системы физических размерностей нашего мироздания находится на пятом уровне иерархии системы (рис. 8). Но и в эзотерике также говорится, что современная цивилизация является "Пятой расой" и что она стоит на пороге "Шестой расы". Но мистика этого совпадения усиливается от того, что на пятом уровне сумма индексов в собственных пространствах этого уровня равна 5 ( i+j=5).

4. СИСТЕМА "БУХГАЛТЕРСКИХ СЧЕТОВ" РУССКОЙ МАТРИЦЫ

Рассмотрим более подробно свойства одной из четырех базисных матриц, представленных на рисунке выше.

T^-1L²	T⁰L¹	T¹L⁰
T^-1L¹	T⁰L⁰	T¹L^-1
T^-1L⁰	T⁰L^-1	T¹L^-2

Рассмотрим в этом базисном "кубике" тождество

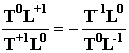расписывая его, с использованием законов сохранения симметрии в виде следующей матрицы

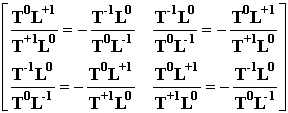Строки этой матрицы по отношению друг к другу отражают закон сохранения зарядовой симметрии, а тождества, стоящие в одной строке -отражают закон сохранения зеркальной симметрии.

Тождества, стоящие на диагоналях матрицы отражают комплексный закон сохранения зеркально-зарядовой симметрии. Их свойства очень хорошо описывается в Книге Книг - Библии:

"И Последний становится Первым".

Теперь можно осознать, что один базисный кубик содержит в себе 4 таких матриц. Следовательно, матрица (рис. 8-3), состоящая из четырех базисных кубиков в общем содержит 16 подобных матриц тождеств. Если учесть, что каждый элемент-тождество в этих матрицах является двойственным тождеством вида

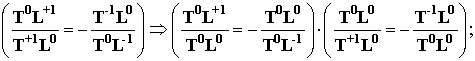то в итоге мы получаем, что один базисный кубик может порождать 32 тождества, т.е. 4 взаимодополнительных базисных "кубиков" (32:8=4).

Система этих тождеств, которые могут сворачиваться в Единицу (Т⁰L⁰) и разворачиваться из нее, позволяет осознать, что взаимоотношения между злотыми числами строится в точном соответствии с правила бухгалтерского учета (Макроэкономика-1).

Актив или Пассив? Дебит или Кредит? Эти слова и их смыслы хорошо известны экономистам. Их смысл состоит в том, что "Нельзя потратить больше, чем имеешь в целом!" Эта прописная бухгалтерская истина отражается в главном бухгалтерском документе - бухгалтерском балансе предприятия, имеющего два взаимодополнительных раздела - Актив (размещенные средства) и Пассив (источники средств).

Это важнейшая перекладина весов бухгалтерского баланса

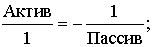Эти весы отражают равновесность (баланс) между суммой Актива и суммой Пассива.

Эти бухгалтерские весы отражают равновесность экономических систем (микроэкономики, макроэкономики, мировой экономики).

Если правая (левая) часть тождества начинает увеличиваться, то соответственно левая (правая) часть тождества начинает уменьшается.

Это тождество характеризует закон сохранения ресурсов в экономике: "Что от одного тела -Актива (или Пассива) убудет, то присовокупится к другому -Пассиву (или Активу). Этот закон целиком и полностью соответствует известным из физики законам сохранения материи (энергии).

Этот закон симметрии (баланса) между Активом и Пассивом в системе бухгалтерского учета проявляется через категории бухгалтерского счета ("Дебит" и "Кредит"), взаимоотношения между которыми описывается аналогичным тождеством

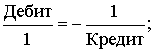Это тождество является базисным бухгалтерским счетом, из которого раскручивается двойная спираль бухгалтерских счетов. Свертка остатков бухгалтерских счетов в итоговый счет порождает заключительную строку любого бухгалтерского баланса.

По этой причине все счета, относящиеся к Активу, носят название Активные счета, в то время как все счета, расположенные в разделе Пассива, носят название Пассивные счета.

Если определить оборот как сумму расходов за расчетный период, то мы можем определить Сальдо конечное для Активных и Пассивных счетов

Для Активных счетов формула для Сальдо конечного будет иметь вид

Сальдо конечное =Сальдо начальное + оборот по Дебиту - оборот по Кредиту

Для Пассивных счетов Сальдо конечное будет считаться уже по иному

Сальдо конечное =Сальдо начальное + оборот по Кредиту - оборот по Дебиту

Таким образом, правила двойного счета, которые проявляются в бухгалтерских проводках, гласят:

"Если мы записали определенную сумму в дебит одного счета,

то мы должны записать эту же сумму в кредит другого счета".

Нетрудно осознать, что система бухгалтерского учета отражает в себе природные операционные механизмы Единого закона эволюции двойственного отношения "Актив-Пассив", которое на начало очередного расчетного периода представляется как Сальдо начальное, равное Сальдо конечное предыдущего расчетного периода.

При этом природные операционные механизмы Единого закона эволюции двойственного отношения "Дебит-Кредит" формируют "четыре базисные стихии" Плана счетов

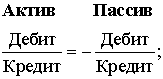Это тождество характеризует законы сохранения симметрии Сальдо Активных и Пассивных счетов, т.е. в бухгалтерских проводках, при определенных ситуациях, счета Актива и Пассива будут являться взаимодополнительными. Бухгалтера хорошо знают эти свойства Плана счетов, когда активные счета проявляют свойства пассивных счетов и наоборот, пассивные счета ведут себя как активные.

Законы сохранения симметрии, отражаемые в бухгалтерском учете, в полной мере отражаются в микроэкономике, макроэкономике и мировой экономике.

Эта двойная бухгалтерия проявляется при анализе любой экономической монады:

"товар-деньги", "спрос-предложение", "безработица-занятость", "инфляция-дефляция", "объект хозяйствования - субъект хозяйствования", и т.д.

Эта двойная бухгалтерия проявляется не только во всех сферах экономики (микроэкономике, макроэкономике, мировой экономике), но и вообще во всех сферах жизнедеятельности современной цивилизации.

И сейчас мы убеждаемся, что Русская матрица построена в точном соответствии с системой бухгалтерских счетов.

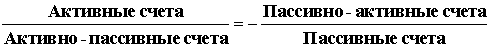Вообще говоря, что наше мироздание характеризуется "Планом счетов" Русской матрицы, в соответствии с которым на каждом уровне иерархии формируется собственный "бухгалтерский баланс" золотосеченных чисел.

Может быть теперь ученые всех направлений, включая руководителей всех уровней смогут, наконец, осмыслить сущность "бухгалтерских проводок", которые они формировать в процессе своей практической и теоретической деятельности. И, в первую очередь, эти "бухгалтерские проводки" должны освоить политические и общественные деятели.

"План счетов" Русской матрицы позволяет осознать правоту концепции Пифагора: "Все есть Число". Каждое число Русской матрицы является золотой константой, которая, по образу и подобию. может порождать собственное мироздание Русских матриц, разворачивая соответствующие "бухгалтерские проводки", а может и сворачиваться в единственное золотое число, которое отражает "бухгалтерский баланс" жизнедеятельности "мироздания".

Это особенно важно понять и осознать руководителям государств, политикам, общественным деятелям и государственным чиновникам, ибо "бухгалтерский баланс" Русской матрицы отражает "сухой остаток" практической и теоретической деятельности руководителей всех уровней иерархии. Если этот "остаток" (Сальдо конечное) увеличивается в результате деятельности того или иного чиновника, это значит, что он по праву занимает доверенный ему пост.

Если "сухой остаток" уменьшается, то такой чиновник должен быть освобожден от занимаемой должности, ибо он, по недомыслию ли, по злому умыслу ли, но содействует сворачиванию расширенного воспроизводства Жизни. Поэтому здесь не будет уже иметь значение к какой национальности многонациональной России будет принадлежать данный чиновник.

Каждому чиновнику будет дан собственный план счетов. И он должен будет периодически показывать всем одну единственную цифру, заверенную "Счетной палатой" -"сухой остаток" его деятельности. Это правило необходимо распространить и на ученых, и на деятелей культуры и искусства. Каждый их них должен "платить по собственным функциональным счетам" и предоставлять для отчетности собственный "сухой остаток".

Природные операционные механизмы Единого закона эволюции двойственного отношения, наиболее ярко проявленные в свойствах Русской матрицы, позволяют все поставить на свое место. И у высокопоставленных чиновников уже не останется возможности лгать и обманывать, загрязняя своими "испражнениями" окружающую среду.

И если люди осознают великую истину "Плана счетов" Русской матрицы, то они смогут смогут осознать величие следующего рисунка.

рис. 8-5

На этом рисунке гиперкуб генетического кода наложен на Древний Цветок Жизни. Теперь нетрудно осознать, что триграммы Книги Перемен, Тайны Древнего Цветка Жизни, двойные спирали генетического кода, и т.д. и т.п., включая "бухгалтерские проводки" по формирования совершенных кристаллов мироздания, каждый из которых имеет свой собственный "бухгалтерский баланс", как в зеркале отражаются в свойствах Русской матрицы и являются следствием природных операционных механизмов Единого закона

5. ЗОЛОТЫЕ ВЕСЫ РУССКОЙ МАТРИЦЫ

План счетов Русской матрицы формирует многомерные и многоуровневые золотые весы, Формируя четыре периода Периодической системы золотых чисел Русской матрицы.

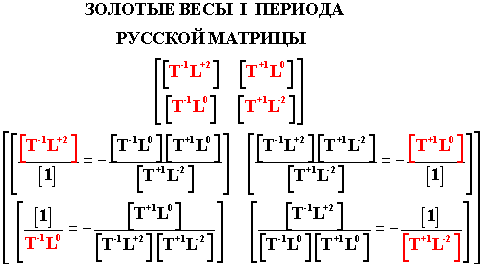Посмотрите, как Замысел Творения I периода Русской матрицы (красный крест) порождает первые четыре базисных золотых оснований пространства-времени. Каждое золотое число, используя монадные весы, строго определенным образом определяется через три других, уже изначально отражая собственную триграммную сущность. Эти четыре основания формируют геном Русской матрицы, отражая строгие правила бухгалтерского счета и учета золотых чисел, формируя на любом уровне "золотой баланс" Русской матрицы. При таком бухгалтерский счете и учете золотых чисел невозможно потерять в Мироздании даже самую элементарную частицу.

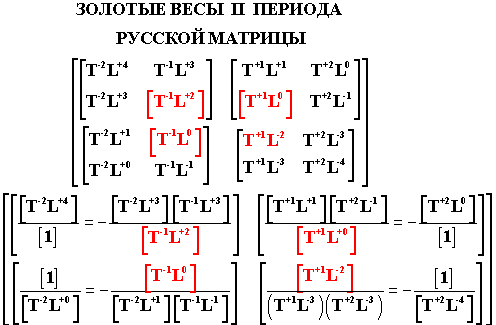Данная матрица состоит из четырех матричных секторов, каждый из которых содержит по две подоболочке, число золотых чисел в которых характеризуется, как в Периодической таблице химических элементов, соотношением 1:3. Причем четыре одномерных подоболочки формируют золотой крест Замысла творения для секторов Русской матрицы следующего уровня иерархии.

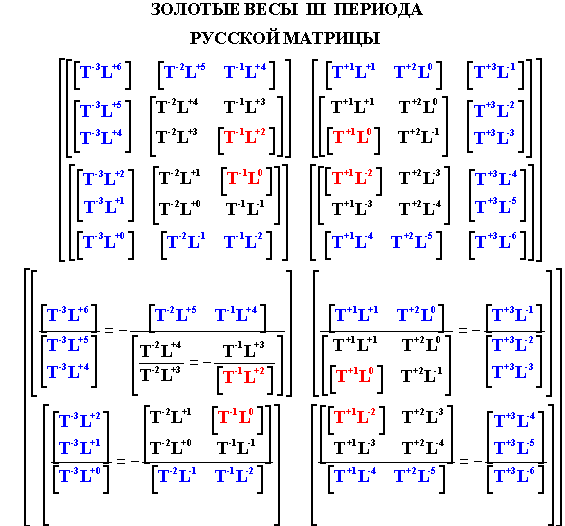В этих матричных весах отношения между числом чисел в подоболочках составляют 1:3:5, что снова совпадает с закономерностью формирования подоболочек и оболочек Периодической системы химических элементов. Кроме того, общее число элементов в III периоде Периодической системы равно

(18,18)=((9,9),(9,9))

Заметим одну важную особенность самой внешней оболочки данного периода. Число золотых чисел в ней равно 5х4=20.

Следующая оболочка Русской матрицы порождает самую сложную оболочку золотых чисел, которая формируется по образу и подобию.

Замечательным свойством многомерных весов Русской матрицы является тот факт, что все внутренние подоболочки и оболочки оказываются уравновешенными (нормированными). Это приводит к тому, что нормированная оболочка любой сложности всегда оказывается на чаше весов одного из четырех секторов матричного тождества. В результате на любом уровне иерархии мы всегда будет иметь "золотой крест".

Сам факт заключения совокупности золотых чисел пространства-времени в матричные скобки символизирует уравновешенность многоуровневого "золотого числа".

При этом на каждом уровне иерархии формируются четыре уникальных золотых базисных чисел пространства-времени (собственный "золотой крест". Вот как вычисляется этот крест для самой сложной оболочки Русской матрицы.

Из этого золотого креста будут сплетаться двойные спирали генетического кода пространства-времени для Русской матрицы более высокого уровня иерархии.

И вот что интересно. Золотые матричные числа взаимодействуют между собой в точном соответствии с правилами умножения матриц (всегда матрица-строка умножается на матрицу-столбец, и наоборот), т.е. перемножаются друг с другом только ортогональные двойственные золотые числа пространства-времени.

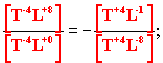Посмотрите, как неукоснительно строго в каждом "золотом кресте" соблюдаются законы сохранения зеркально-зарядовой симметрии.

Кроме того, данное матричное тождество IV периода Русской матрицы пространства и времени содержит 8х8=64 двойственных числа. Поэтому можно сказать, что свойства золотых чисел Русской матрицы пространства-времени сплетаться в двойные спирали генетического кода пространства -времени дает дополнительную информацию о триграммах и гексаграммах Книги Перемен, в которой теперь даже невооруженным глазом видно, что каждая гексаграмма есть "двойственное число", сплетенное из триграмм.

Точно также плетутся и двойные спирали химических элементов. Кроме того, свойства золотых чисел Русской матрицы дает много дополнительной информации о генетическом коде, и не только. Золотые кресты Русской матрицы формируют геномы вселенных, по образу и подобию.

6. РУССКАЯ МАТРИЦА И КРИСТАЛЛЫ МИРОЗДАНИЯ

Русская матрица обладает многими "магическими" свойствами.

Главная "золотая" диагональ Русской матрицы несет в себе сокровенные тайны Замысла творения Русской матрицы. Золотая диагональ несет в себе тайну законов симметрии высших измерений, а вся Русская матрица представляет собой проекцию на плоскость "кристалла" высших измерений. Русская матрица позволяет, зная законы сохранения симметрии двойственного отношения (монады), выйти за пределы осознанного мира и "увидеть" прекрасный мир высших измерений. "Плоскарик" МОЖЕТ осознать мир высших измерений.

На странице "О структуре измерений", и других, мы рассматривали свойства Платоновых тел.

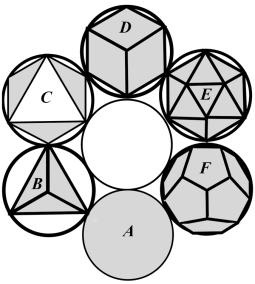рис.9

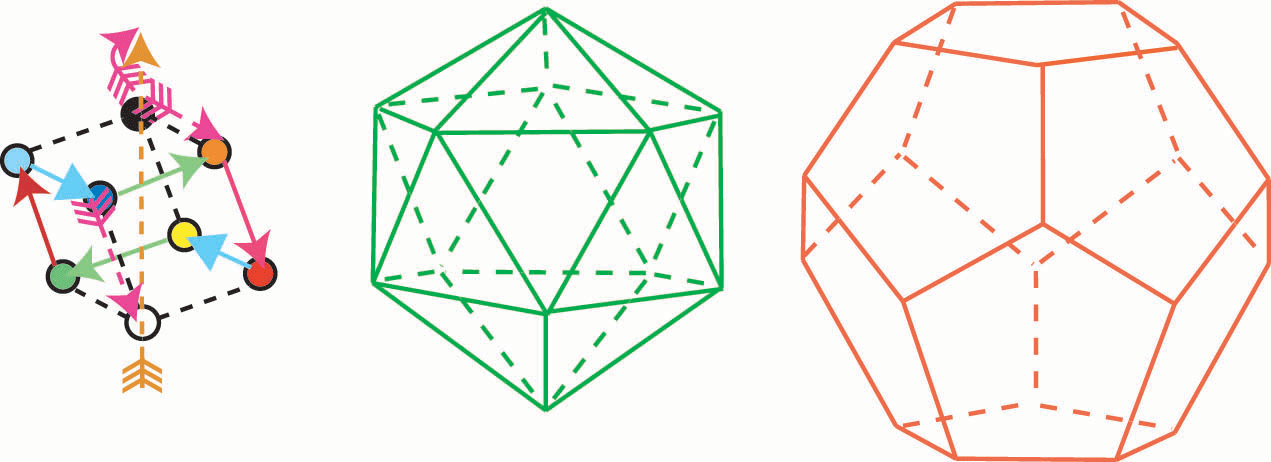Куб Икосаэдр Додекаэдр

рис.10

Каждый из этих кристаллов отражает симметрию собственного мироздания. Кроме того, они вписываются друг в друга.

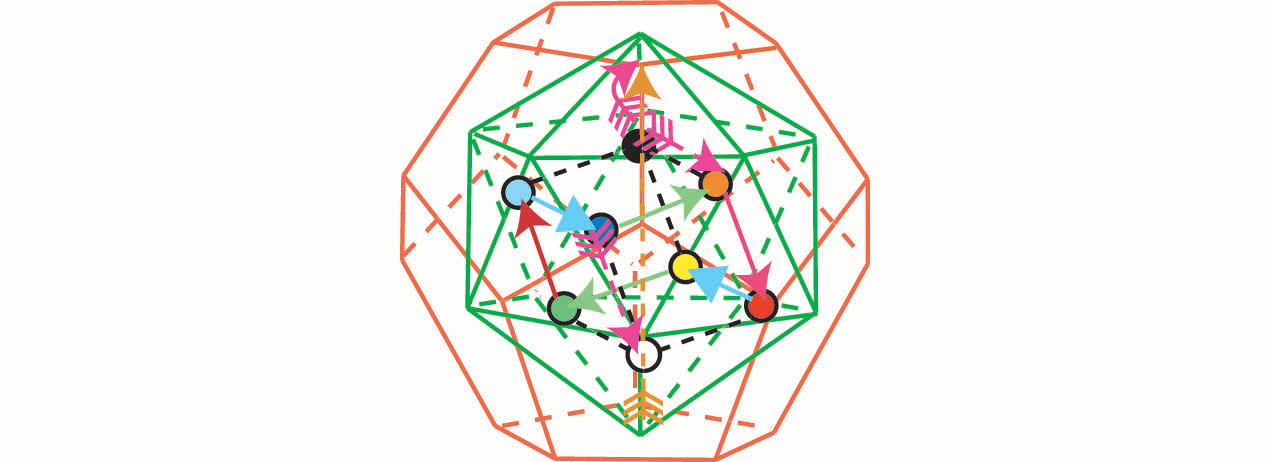рис.11

Симметрия этих кристаллов отражается в низших измерениях, в форме магических матриц (Магия чисел).

рис.12

Видите, как последовательно формируются вершины кристаллов, как идет группировка четных и нечетных вершин, как формируются на плоскости законы сохранения высших измерений?

Преемственность формирования Платоновых тел отражается в их проекциях на плоскость, что может свидетельствовать о том, что куб, икосаэдр и додекаэдр могут формировать Великий Предел Платоновых тел - "фитонную Сферу". В этом "фитоне" 8+12+20=40 вершин. Из смысла Единого закона следует, что и у этого Великого предела существует собственная монада, имеющая две вершины.

Пожалуй, наиболее рельефно сущность числа "сорок +два" отражена в храмовой исповеди, которая произносилась в Комнате Маата в Египетском Храме Инициаций. Маат - это египетское слово, обозначающее "Истина", т.е. Комната Маат -это Храм Истины. .

"Почтение Тебе, о Великий Господь, Властелин Истины, я пришел к Тебе, о мой Господин, и я пришел сюда, чтобы осознать Твои Законы. Я знаю Тебя, и я в гармонии с Тобой, и Твои два и еще сорок законов существуют с Тобой с этом Храме Маата. С Истиной я пришел к Созвучию с Тобой, и поместил Маат в свой Разум и Душу......".

Но существует еще одно сакральное число -"сорок сороков". Это самый совершенный гиперкристалл мироздания. По образу и подобию, существуют и иные совершенные гиперкристаллы мироздания (гипер куб, гиперикосаэдр, гипердодекаэдр). В этих гиперкристаллах каждая вершина является соответствующим кристаллом. И каждый гиперкристалл может иметь свою проекцию на плоскость и отражать в ней свои свойтва, которые проявляются в магии матриц.

И свойства магических матриц проявляется уже в базисной матрице - энеаграмме.

РЕЗЮМЕ

Хотелось бы, чтобы читатели данной страницы задали себе следующие вопросы и постарались бы ответить не них самостоятельно.

1. Сколько лет еще понадобится, чтобы прозрачная Тайна Единого закона стала достоянием людей? Сколько лет они будут еще идти на поводу своего бессознательного Я: "Этого не может быть, потому что не может быть никогда"?

2. Сколько еще лет они будут пытаться свой уникальный внутренний мир "напяливать" на весь окружающий их внешний мир, и , считая его недостаточно объективным, вычленять из него все, что не вяжется с их представлениями об окружающей действительности? Ведь нельзя же собственные Единые знания, полученные в процессе образования и воспитания, и содержащие различные искусственные модели и правила согласования собственных домыслов с окружающей действительностью, путать со Знанием Единого, в котором, в принципе, не существует отклонений от Истины, какой бы они ни была.

По этой причине Знание Единого позволяет верифицировать Единые, но частные, знания.

3. Может быть настала пора таким ученым вручить собственный "План счетов" и потребовать от них "бухгалтерский баланс" с отчетом о проделанной работе?

Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать о всех замеченных ошибках, некорректных формулировках.

Книги "Основы милогии", "Милогия" могут быть высланы в Ваш адрес наложенным платежом,

URL1: milogy.net

e-mail: [email protected]

Карта сайта

rss

Карта