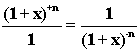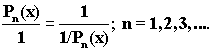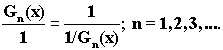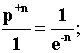БИНОМИАЛЬНАЯ СЛАВЯНСКАЯ МАТРИЦА
5.
ВЕСЫ ПРОИЗВОДЯЩИХ ФУНКЦИЙ
Резонансные отношения характеризуют инвариантные переходы в матрице из
одного состояния в другое, используя весы матрицы
 рис. 17
Это тождество возникает только тогда когда между полюсами
монады будет существовать баланс "спроса" и "предложения" вида
рис. 17
Это тождество возникает только тогда когда между полюсами
монады будет существовать баланс "спроса" и "предложения" вида
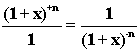 Посмотрите, какие отношения гармонии существуют между
Образом и его Подобием в каждом полюсе монады?
И
точно такие же рыночные гармонические взаимоотношения существуют и
между полюсами монады. Точно такие же отношения существуют и между
взаимодополнительнымии монадами, в которых монады уже являются
взаимодополнительными полюсами.
И такие рыночные отношения формируются, по образу и подобию, во всей
Вселенной.
Применительно к производящим функциям это тожество можно записать в
следующем виде
Посмотрите, какие отношения гармонии существуют между
Образом и его Подобием в каждом полюсе монады?
И
точно такие же рыночные гармонические взаимоотношения существуют и
между полюсами монады. Точно такие же отношения существуют и между
взаимодополнительнымии монадами, в которых монады уже являются
взаимодополнительными полюсами.
И такие рыночные отношения формируются, по образу и подобию, во всей
Вселенной.
Применительно к производящим функциям это тожество можно записать в
следующем виде
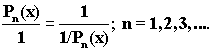
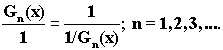 Эти
тождества характеризуются законом сохранения зарядовой симметрии, в соответствии с принципами самоорганизации (Cамоорганизация).
Необходимо отметить, что учет закона сохранения зеркальной симметрии
приведет к тому, что правая и левая части тождеств будут иметь разные знаки.
И если в какой-то момент в монаде возникают возмущения, то возникает Сила
саморегуляции, которая формирует баланс "спроса" и "предложения на новом
уровне, расталкивая или приталкивая полюса монады.
Наиболее ярким примером гармоничных рыночных отношений является
Периодическая система химических элементов, в которой каждый химический
элемент "живет" свято соблюдая баланс рыночных отношений между протонными и
электронными оболочками.
Эти
тождества характеризуются законом сохранения зарядовой симметрии, в соответствии с принципами самоорганизации (Cамоорганизация).
Необходимо отметить, что учет закона сохранения зеркальной симметрии
приведет к тому, что правая и левая части тождеств будут иметь разные знаки.
И если в какой-то момент в монаде возникают возмущения, то возникает Сила
саморегуляции, которая формирует баланс "спроса" и "предложения на новом
уровне, расталкивая или приталкивая полюса монады.
Наиболее ярким примером гармоничных рыночных отношений является
Периодическая система химических элементов, в которой каждый химический
элемент "живет" свято соблюдая баланс рыночных отношений между протонными и
электронными оболочками.
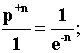 Осознайте великую гармонию этих резонансных взаимодействий. В каждом атоме,
с порядковым номером n,
между протонными и электронными подоболочками и оболочками существует баланс
взаимоотношений. И пока такой баланс существует, атом химического элемента
обладает стабильностью.
Видите, какой "массивный" протон, а ведь он может управляться "маленьким"
электроном. Помните закон рычага - "выигрываешь в силе- проигрываешь в
расстоянии". В протоне собственный внутренний радиус невелик, а масса, по
сравнению с электроном велика. В электроне же наоборот. У него радиус
вращения большой, а масса невелика. Поэтому в результате возникающих
возмущений не только протон может управлять электроном, но и электрон может
влиять на состояние протона, до такой степени. что электрон может
"переродиться" в протон. Это конечно гипотеза, которую можно отнести к
разряду фантастических, но весы монады химических элементов, отражающие
единство сущностного и функционального такую возможность допускают.
А теперь постарайтесь ответить себе на вопрос - являются ли рыночными те
отношения в мировой экономике, которые всемерно внедряются на всех уровнях
бытия современного человечества?
Разве можно назвать отношениями
гармонии не стремление к гармоничному развитию, а стремлениями к
навязывающим другим (производителям, потребителям, партнерам, странам
и государствам) своей воли?
6.
ДВОЙНЫЕ СПИРАЛИ ПРОИЗВОДЯЩИХ ФУНКЦИЙ
На
странице "Преемственность" мы уже рассматривали
свойства биномиальных производящих функций, порождаемых следующими операторами.
Осознайте великую гармонию этих резонансных взаимодействий. В каждом атоме,
с порядковым номером n,
между протонными и электронными подоболочками и оболочками существует баланс
взаимоотношений. И пока такой баланс существует, атом химического элемента
обладает стабильностью.
Видите, какой "массивный" протон, а ведь он может управляться "маленьким"
электроном. Помните закон рычага - "выигрываешь в силе- проигрываешь в
расстоянии". В протоне собственный внутренний радиус невелик, а масса, по
сравнению с электроном велика. В электроне же наоборот. У него радиус
вращения большой, а масса невелика. Поэтому в результате возникающих
возмущений не только протон может управлять электроном, но и электрон может
влиять на состояние протона, до такой степени. что электрон может
"переродиться" в протон. Это конечно гипотеза, которую можно отнести к
разряду фантастических, но весы монады химических элементов, отражающие
единство сущностного и функционального такую возможность допускают.
А теперь постарайтесь ответить себе на вопрос - являются ли рыночными те
отношения в мировой экономике, которые всемерно внедряются на всех уровнях
бытия современного человечества?
Разве можно назвать отношениями
гармонии не стремление к гармоничному развитию, а стремлениями к
навязывающим другим (производителям, потребителям, партнерам, странам
и государствам) своей воли?
6.
ДВОЙНЫЕ СПИРАЛИ ПРОИЗВОДЯЩИХ ФУНКЦИЙ
На
странице "Преемственность" мы уже рассматривали
свойства биномиальных производящих функций, порождаемых следующими операторами.
Оператор развертки:
P0(x)=(1+x)-1=x0-x1+x2-x3+x4-x5....
Оператор свертки:
1/P0(x)=1/(1+х)-1=(1+x)+1;
Оператор удвоения:
G0(x)=
(1-х)+1=1-х+х2-х3+х4-х5+...
Оператор раздвоения: 1/G0(x)=1/(1-x)1=(1-x)-1;
Применяя к
Единице
оператор
развертывания, мы получили следующий
набор производящих функций
P0(x)=1;
P1(x)=(1-x)-1=1-x+x2-x3+
...
P2(x)=(1-x)-2=1-2x+3x2-4x3+...
P3(x)=(1-x)-3=1-3x+6x2-10x3+...
P4(x)=(1-x)-4=1-5x+14x2-30x3+...
Применяя
к функциям
Pi(x),
i=1,2,3,...оператор удвоенияG0(x),
мы получили следующие производящие функции
G0(x)=1+х;
G1(x)=1-2x+2x2-2x3+
...
G2(x)=1-3x+5x2-7x3+
...
G3(x)=1-4x+
9x2-16x3+
...
G4(х)=1-5х+14х2-30х3+...
Увязывая
эти производящие функции
Pn(x)
и Gn(х)
в единую схему, мы
получили
следующие двойные спирали.
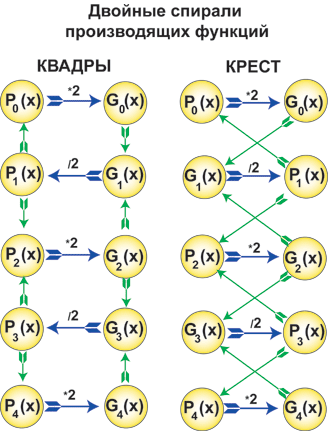 Рис.
12
Из рис. 12 можно получить первое представление, чем отличается квадра от креста. В кресте двойная цепочка вьется как лента Мёбиуса. Здесь в
левом столбце креста производящие функции обладают иньскими свойствами
(точка синтеза двух входящих потока с последующим порождением одного янского
потока. В правом столбце каждая функция обладает янскими свойствами
(точка бифуркации-один входящий поток и два выходящих). Еслив "кресте мы будем
иметь две цепочки с противоположными свойствами (ян и инь), то в "квадре" мы
будем иметь другую ситуацию. Здесь каждая квадра сопрягается с
соседними как шестеренка в часовом механизме.
В
двойных спиралях (рис. 12) имеют
место следующие пропорции между "разноименными" производящими
функциями
Рис.
12
Из рис. 12 можно получить первое представление, чем отличается квадра от креста. В кресте двойная цепочка вьется как лента Мёбиуса. Здесь в
левом столбце креста производящие функции обладают иньскими свойствами
(точка синтеза двух входящих потока с последующим порождением одного янского
потока. В правом столбце каждая функция обладает янскими свойствами
(точка бифуркации-один входящий поток и два выходящих). Еслив "кресте мы будем
иметь две цепочки с противоположными свойствами (ян и инь), то в "квадре" мы
будем иметь другую ситуацию. Здесь каждая квадра сопрягается с
соседними как шестеренка в часовом механизме.
В
двойных спиралях (рис. 12) имеют
место следующие пропорции между "разноименными" производящими
функциями
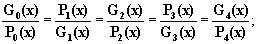 Из этих пропорций непосредственно можно получить все формулы для определения
любого члена двойной цепочки, например,
Из этих пропорций непосредственно можно получить все формулы для определения
любого члена двойной цепочки, например,
 Посмотрите, в этих
двойных спиралях каждая из функций (Pn(x)
и Gn(х)) играет роль точки
бифуркации, в которой происходит раздвоение, или точкой синтеза (удвоение).
Каждая производящая функция является либо точкой синтеза (удвоение), либо точкой
бифуркации (раздвоение).
В квадрах
точки бифуркации (раздвоения) и точки синтеза (удвоение) распределены в
столбцах , сменяя друг друга. В правой спирали биномиальных производящих
функций (крест) они группируются по столбцам. В первой группе (левый
столбец) располагаются точки синтеза (удвоения). Во втором столбце -точки
бифуркации (раздвоения).
Таким образом, в процессе порождения биномиальных производящих функций
формируется двойная спираль. Одна спираль представляет собой янский восходящий
поток, а другая -иньский восходящий поток.
Хотелось бы обратить
внимание на свойство точек бифуркации. В этой точке эволюционный поток
раздваивается.
Один поток из янской вершины направляется в "Будущее",
к иньской вершине. Другой поток направляется в "Прошлое",
в предыдущий иньский поток.
Может быть, в
этой связи, стоит более внимательно отнестись к мнению видных российских ученых,
которые недвусмысленно заявляют, что современное общество находится сегодня в
точке бифуркации, и что в этой связи необходимо менять мышление. Вот только
какое оно-это новое мышления, никто из них ничего не говорит. Но, говоря он
новом мышлении людей, они, почему-то все выставляют себя лично за "скобки".
Может быть, они уже перестроили свое мышление?
Но почему тогда они так упорно молчат о том, какое оно-это самое новое
мышление?
Может
быть, нашим ученым, следует более внимательно присмотреться к прогнозам
свыше (О Шестой расе), в которых прямо и
недвусмысленно объявляется, что современный жизнепоток человечества
переведен уже в 6-расу и что сейчас все люди уже разделены на два потока. Они
поток будет направлен в "Будущее",
в иньскую точку спирали жизнепотока, другой будет направлен в "откат", в иньскую
точку синтеза, в которую войдет и нижележащий восходящий поток (полуживотных).
Может быть, это тоже
мистика? Может быть, и дальше будем прикидываться
дурачками -"ничего не вижу, ничего не слышу"?
Может быть, пришла
пора осознать, что именно двойные спирали биномиальных производящих
функций лежат в основе генетического кода Вселенной, генотипом которого являются
всего 8 операторов, порождающих все биномиальные производящие
функции, в которых все коэффициенты являются биномиальными.
Приведенные выше
тождества и схемы эволюции производящих функций будут справедливы и для функций
*Pn(x) и
*Gn(х).
Посмотрите, в этих
двойных спиралях каждая из функций (Pn(x)
и Gn(х)) играет роль точки
бифуркации, в которой происходит раздвоение, или точкой синтеза (удвоение).
Каждая производящая функция является либо точкой синтеза (удвоение), либо точкой
бифуркации (раздвоение).
В квадрах
точки бифуркации (раздвоения) и точки синтеза (удвоение) распределены в
столбцах , сменяя друг друга. В правой спирали биномиальных производящих
функций (крест) они группируются по столбцам. В первой группе (левый
столбец) располагаются точки синтеза (удвоения). Во втором столбце -точки
бифуркации (раздвоения).
Таким образом, в процессе порождения биномиальных производящих функций
формируется двойная спираль. Одна спираль представляет собой янский восходящий
поток, а другая -иньский восходящий поток.
Хотелось бы обратить
внимание на свойство точек бифуркации. В этой точке эволюционный поток
раздваивается.
Один поток из янской вершины направляется в "Будущее",
к иньской вершине. Другой поток направляется в "Прошлое",
в предыдущий иньский поток.
Может быть, в
этой связи, стоит более внимательно отнестись к мнению видных российских ученых,
которые недвусмысленно заявляют, что современное общество находится сегодня в
точке бифуркации, и что в этой связи необходимо менять мышление. Вот только
какое оно-это новое мышления, никто из них ничего не говорит. Но, говоря он
новом мышлении людей, они, почему-то все выставляют себя лично за "скобки".
Может быть, они уже перестроили свое мышление?
Но почему тогда они так упорно молчат о том, какое оно-это самое новое
мышление?
Может
быть, нашим ученым, следует более внимательно присмотреться к прогнозам
свыше (О Шестой расе), в которых прямо и
недвусмысленно объявляется, что современный жизнепоток человечества
переведен уже в 6-расу и что сейчас все люди уже разделены на два потока. Они
поток будет направлен в "Будущее",
в иньскую точку спирали жизнепотока, другой будет направлен в "откат", в иньскую
точку синтеза, в которую войдет и нижележащий восходящий поток (полуживотных).
Может быть, это тоже
мистика? Может быть, и дальше будем прикидываться
дурачками -"ничего не вижу, ничего не слышу"?
Может быть, пришла
пора осознать, что именно двойные спирали биномиальных производящих
функций лежат в основе генетического кода Вселенной, генотипом которого являются
всего 8 операторов, порождающих все биномиальные производящие
функции, в которых все коэффициенты являются биномиальными.
Приведенные выше
тождества и схемы эволюции производящих функций будут справедливы и для функций
*Pn(x) и
*Gn(х).
Операторы
развертки и свертки являются взаимодополнительными, т.е. для производящих
функций, порожденных этими операторами будет справедливо тождество
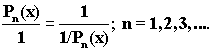 Аналогично, операторы
удвоения и раздвоения, порождают производящие функции, для которых будет
справедливо тождество
Аналогично, операторы
удвоения и раздвоения, порождают производящие функции, для которых будет
справедливо тождество
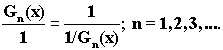 Рассматривая эти
тождества, можно заметить, что правая и левая часть пропорции отличаются друг от
друга как мир и
антимир.
Данные
свойства являются настолько тривиальными, что ни математики, ни физики, не
обращают на них никакого влияния, настолько они всеобщие. А напрасно. За ними
стоит, например, тайна дробных зарядов физических кварков. Эти частицы в нашем
мире кажутся состоящими из дробных зарядов.
Рассматривая эти
тождества, можно заметить, что правая и левая часть пропорции отличаются друг от
друга как мир и
антимир.
Данные
свойства являются настолько тривиальными, что ни математики, ни физики, не
обращают на них никакого влияния, настолько они всеобщие. А напрасно. За ними
стоит, например, тайна дробных зарядов физических кварков. Эти частицы в нашем
мире кажутся состоящими из дробных зарядов.
На самом деле, в зазеркалье (который физики
отождествляют с физическим вакуумом) "кварки" имели целый заряд. Но вот когда
они попытались объединиться в частицу с тройственным зарядом (в соответствии,
например, с производящей функцией
P(x), то произошло самонормирование производящей функции и она трансформировалась в
1/P(x).
В результате мы получили одну частицу с единичным
зарядом, а составляющие ее части оказались с
дробным зарядом.
Из атомной физики известно, что радиусы боровских орбит
удовлетворяют следующим соотношениям.
1:4:9:16:
Связывая эти соотношения с производящей
функцией
G3(x)=1-4x+
9x2-16x3+
и сопоставляя этому ряду
взаимодополнительный, мы придем к ряду
*G3(x)=2-8x+
18x2-32x3+
Повторное копирование порождает
структуру Периодической таблицы химических элементов.
(2,0,8,0,18,0,32,...)
(2,0,8,0,18, 0,32,...)
(2,2,8,8, 18,18,32,32,...)
Таким образом, мы определили класс производящих функций структур, который
учитывает закономерность двойственности иерархических систем (как внутреннюю,
так и внешнюю). Кроме того, этот класс производящих структур является
“замкнутым”, ибо мы каждый раз будем получать инвариантные структуры, не
выходящие за пределы данного класса структур.
Дополняя рассмотренные выше опреаторы
Оператор
развертки:
P0(x)=(1+x)-1=x0-x1+x2-x3+x4-x5....
Оператор свертки:
1/P0(x)=1/(1+х)-1=(1+x)+1;
Оператор удвоения:
G0(x)=
(1-х)+1=1-х+х2-х3+х4-х5+...
Оператор раздвоения: 1/G0(x)=1/(1-x)1=(1-x)-1;
взаимодополнительными
*Оператор развертки:
*P0(x)=(1-x)-1=x0+x1+x2+x3+x4+x5....
*Оператор свертки:
1/*P0(x)=1/(1-х)-1=(1=x)+1;
*Оператор удвоения:
*G0(x)=
(1+х)+1=1+х;
*Оператор раздвоения: 1/*G0(x)=1/(1-x)1=(1-x);
Мы получим 8 операторов
производящих функций, порождающих двойные спирали.
На странице "Русская
матрица" мы показали, что золотосеченные числа образуют "весы"
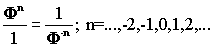 Такие "весы" имеются и
в приведенных на рис. 3-2 схемах. Так для двойной спирали "крест" имеют
место следующие пропорции
Такие "весы" имеются и
в приведенных на рис. 3-2 схемах. Так для двойной спирали "крест" имеют
место следующие пропорции
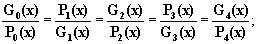 Из этих пропорций непосредственно можно получить все формулы для определения
любого члена двойной цепочки, например,
Из этих пропорций непосредственно можно получить все формулы для определения
любого члена двойной цепочки, например,
 А теперь обратите
внимание на цепочку генетического кода
А теперь обратите
внимание на цепочку генетического кода
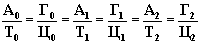 Видите, в этой
цепочке нет прямых соединений А-Г, Ц-Т. Они запрещены природой, но сущность этих
запретов легко вытекает их биномиальных производящих функций. Эти соединения
относятся к одноименным (янским, или иньским) цепочкам.
Их пропорций видим,
что если запрещенные комбинации А-Г могут относиться к янской цепочке, то
запрещенные комбинации Ц-Т будут однозначно относятся к иньским цепочкам.
Если мы начнем строить
двойную спираль с аденина (А), то мы получим следующие две цепочки
янская цепочка - Т0, Ц0, Т1,
Ц1, Т2,
Ц2, ....
иньская цепочка - А0, Г0, А1,
Г1, А2,....
Но мы уже
знаем, что в иньской цепочке каждое звено является точкой синтеза - на входе она
взаимодействует с двумя элементами а на выходе с одним.
В янской цепочке
-наоборот, на входе эта точка взаимодействует с одним элементом, а на выходе
соединяется с двумя (точка бифуркации).
Поэтому из пропорций
мы можем получить следующие выражения для определения значений генетического
кода
для янской цепочки (умножить-разделить-разделить)
Видите, в этой
цепочке нет прямых соединений А-Г, Ц-Т. Они запрещены природой, но сущность этих
запретов легко вытекает их биномиальных производящих функций. Эти соединения
относятся к одноименным (янским, или иньским) цепочкам.
Их пропорций видим,
что если запрещенные комбинации А-Г могут относиться к янской цепочке, то
запрещенные комбинации Ц-Т будут однозначно относятся к иньским цепочкам.
Если мы начнем строить
двойную спираль с аденина (А), то мы получим следующие две цепочки
янская цепочка - Т0, Ц0, Т1,
Ц1, Т2,
Ц2, ....
иньская цепочка - А0, Г0, А1,
Г1, А2,....
Но мы уже
знаем, что в иньской цепочке каждое звено является точкой синтеза - на входе она
взаимодействует с двумя элементами а на выходе с одним.
В янской цепочке
-наоборот, на входе эта точка взаимодействует с одним элементом, а на выходе
соединяется с двумя (точка бифуркации).
Поэтому из пропорций
мы можем получить следующие выражения для определения значений генетического
кода
для янской цепочки (умножить-разделить-разделить)
 для иньской цепочки (умножить-умножить-разделить):
для иньской цепочки (умножить-умножить-разделить):
 Обратите внимание на двойную спираль
"крестного хода". Здесь в левом и правом столбце запрещены переходы между
производящими функциями. Поскольку левый столбец обладает свойствами иньской
цепочки, а правый -янской, то из схемы видно, что в двойной спирали ДНК все эволюционные потоки образуют взаимодополнительные
цепочки
иньская-
P0(x),G1(x),P2(x),G3(x),P4(x),
янская-
G0(x),P1(x),G2(x),P3(x),G4(x),
По
аналогии, для производящих функций этих цепочек можно получить следующие
формулы:
для иньской цепочки
(умножить-умножить-разделить)
Обратите внимание на двойную спираль
"крестного хода". Здесь в левом и правом столбце запрещены переходы между
производящими функциями. Поскольку левый столбец обладает свойствами иньской
цепочки, а правый -янской, то из схемы видно, что в двойной спирали ДНК все эволюционные потоки образуют взаимодополнительные
цепочки
иньская-
P0(x),G1(x),P2(x),G3(x),P4(x),
янская-
G0(x),P1(x),G2(x),P3(x),G4(x),
По
аналогии, для производящих функций этих цепочек можно получить следующие
формулы:
для иньской цепочки
(умножить-умножить-разделить)
 для янской цепочки
(умножить-разделить-разделить)
для янской цепочки
(умножить-разделить-разделить)
 Таким образом,
общность свойств биномиальных производящих
функций со свойствами азотистых оснований генетического кода позволила
выявить глубинные основы формирования двойных спиралей ДНК, позволила
осознать, что азотистые основания формируют собственные янские и иньские
цепочки.
Посмотрите на формулы, определяющие
структуру того или иного элемента янской или иньской цепочки и обратите
внимание на присутствие в первом члене цепочек фиктивного элемента, т.е. уже в
самое первое выражение заложена иньская основа -способность породить начало
новой цепочки.
7. ДВОЙНАЯ СПИРАЛЬ
ЭВОЛЮЦИИ МАТРИЦЫ
Рассмотренные выше биномиальные производящие функции можно называть янскими, ибо
они способствуют раздвоению целого на части, отражая библейское "время
разбрасывать камни". И выше мы уже показали, что эти функции являются полными,
т.е. они способны отражать в себе, по образу и подобию и янский и иньский
аспекты. Теперь мы воочию покажем, что совокупность всех производящих функций,
порождает матричные миры, в которых янский и иньский аспекты очень четко
разделены "в матричном пространстве", отражая свои уникальные свойства.
Рассмотрим механизмы формирования янских биномиальных матриц,
производя суммирование членов матриц относительно главной, единичной диагонали
матрицы.
1.
Матрица
P0(x) =>P1(x),
Таким образом,
общность свойств биномиальных производящих
функций со свойствами азотистых оснований генетического кода позволила
выявить глубинные основы формирования двойных спиралей ДНК, позволила
осознать, что азотистые основания формируют собственные янские и иньские
цепочки.
Посмотрите на формулы, определяющие
структуру того или иного элемента янской или иньской цепочки и обратите
внимание на присутствие в первом члене цепочек фиктивного элемента, т.е. уже в
самое первое выражение заложена иньская основа -способность породить начало
новой цепочки.
7. ДВОЙНАЯ СПИРАЛЬ
ЭВОЛЮЦИИ МАТРИЦЫ
Рассмотренные выше биномиальные производящие функции можно называть янскими, ибо
они способствуют раздвоению целого на части, отражая библейское "время
разбрасывать камни". И выше мы уже показали, что эти функции являются полными,
т.е. они способны отражать в себе, по образу и подобию и янский и иньский
аспекты. Теперь мы воочию покажем, что совокупность всех производящих функций,
порождает матричные миры, в которых янский и иньский аспекты очень четко
разделены "в матричном пространстве", отражая свои уникальные свойства.
Рассмотрим механизмы формирования янских биномиальных матриц,
производя суммирование членов матриц относительно главной, единичной диагонали
матрицы.
1.
Матрица
P0(x) =>P1(x),
|
В |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
А* |
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2-1 |
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3-1 |
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
4-1 |
|
5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
5-1 |
|
4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
6-1 |
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
7-1 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
8-1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9-1 |
|
А |
9 |
8-1 |
7-1 |
6-1 |
5-1 |
4-1 |
3-1 |
2-1 |
1 |
В* |
рис. 13
В этой
матрице и главная и ортогональная к ней диагонали являются единичными.
Но
уже в этой матрице чувствуется мистика двойной спирали.
Складывая симметрично расположенные единицы на главной и ортогональной к ней
диагонали, мы и по горизонтали, и по вертикали получим ряды
P0(x)=1,1,1,1,1,1,1,1,1,...
P0(x)=0,1,1,1,1,1,1,1,1,1,...
G0(x)=1,2,2,2,2,2,2,2,2,...
Здесь
1-это центр симметрии
матрицы, где пересекаются главная и ортогональная диагонали.
И
относительно этого центра в матрице уравновешены все числа.
Обозначая сумму чисел (от главной диагонали) по строкам через
P,
а взаимодополнительную сумму в противоположной половине главной диагонали через
P-1,
мы получим первые представления о
матричных весах:
iP=(jP)-1. Это
уникальное тождество будет иметь место только в одном единственном случае, когда
i=j.
Таким
образом, легко осознать, что числа в матрице отражают рыночные механизмы
взаимоотношений спроса и предложения товаров в экономике. Снова мистическое
совпадение?
Посмотрите, как, по образу и подобию этой
матрицы формируются и все другие
янские матрицы.
Основная особенность этих матриц заключается в том, что числа, стоящие в этих
матрицах, порождаются биномами Ньютона с отрицательными целыми числами,
например,
Pn(x)=(1+x)-n;
Gn(x)=(1-х)Pn(x)=(1-х)(1+x)-n;
2.
Матрица
P1(x)
=>P2(x).
|
В |
45 |
36 |
28 |
21 |
15 |
10 |
6 |
3 |
1 |
А* |
|
45 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
1 |
|
36 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
1/2 |
2-1 |
|
28 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
1/2 |
1/3 |
5-1 |
|
21 |
6 |
5 |
4 |
3 |
2 |
1 |
1/2 |
1/3 |
1/4 |
10-1 |
|
15 |
5 |
4 |
3 |
2 |
1 |
1/2 |
1/3 |
1/4 |
1/5 |
15-1 |
|
10 |
4 |
3 |
2 |
1 |
1/2 |
1/3 |
1/4 |
1/5 |
1/6 |
21-1 |
|
6 |
3 |
2 |
1 |
1/2 |
1/3 |
1/4 |
1/5 |
1/6 |
1/7 |
28-1 |
|
3 |
2 |
1 |
1/2 |
1/3 |
1/4 |
1/5 |
1/6 |
1/7 |
1/8 |
36-1 |
|
1 |
1 |
1/2 |
1/3 |
1/4 |
1/5 |
1/6 |
1/7 |
1/8 |
1/9 |
45-1 |
|
А |
1 |
3-1 |
6-1 |
10-1 |
15-1 |
21-1 |
28-1 |
36-1 |
45-1 |
В* |
рис. 14
Эта
матрица обладает совершенно удивительными свойствами.
Порождая
функцию
P2(x),
она одновременно порождает
и функцию G1(x),
которая располагается в
матрице на диагонали, ортогональной главной. Природа этого явления будет
обоснована ниже.
P1(x)=1,2,3,4,5, 6,
7,...
P1(x)=0,1,2,3,4,
5, 6, 7,..
G1(x)=1,3,5,7,9,11,13, 15,...
3.
Матрица
G0(x) =>G1(x),
Рассмотрим теперь свойства другой ветви производящих функций, порождающих
соответствующие матрицы.
|
В |
17 |
15 |
13 |
11 |
9 |
7 |
5 |
3 |
1 |
А* |
|
17 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
|
15 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1/2 |
3-1 |
|
13 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1/2 |
1/2 |
5-1 |
|
11 |
2 |
2 |
2 |
2 |
2 |
1 |
1/2 |
1/2 |
1/2 |
7-1 |
|
9 |
2 |
2 |
2 |
2 |
1 |
1/2 |
1/2 |
1/2 |
1/2 |
9-1 |
|
7 |
2 |
2 |
2 |
1 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
11-1 |
|
5 |
2 |
2 |
1 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
13-1 |
|
3 |
2 |
1 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
15-1 |
|
1 |
1 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
17-1 |
|
А |
1-1 |
3-1 |
5-1 |
7-1 |
9-1 |
11-1 |
13-1 |
15-1 |
17-1 |
В* |
рис. 15
Посмотрите, здесь главная диагональ представляет собой ряд
P0(x)=1,1,1,1,1,1,1,1,1,...
а
ортогональная к главной -уже ряд
G0(x)=1,2,2,2,....
т.е.
переход к ортогональной диагонали вызывает удвоение первого ряда (со сдвигом).
P0(x)=1,1,1,1,1,1,1,1,1,...
P0(x)=0,1,1,1,1,1,1,1,1,1,...
G0(x)=1,2,2,2,2,2,2,2,2,2,...
4.
Матрица
G1(x)
=>G2(x),
|
В |
92 |
82 |
72 |
62 |
52 |
42 |
32 |
22 |
1 |
А* |
|
92 |
17 |
15 |
13 |
11 |
9 |
7 |
5 |
3 |
1 |
1-2 |
|
82 |
15 |
13 |
11 |
9 |
7 |
5 |
3 |
1 |
1/3 |
2-2 |
|
72 |
13 |
11 |
9 |
7 |
5 |
3 |
1 |
1/3 |
1/5 |
3-2 |
|
62 |
11 |
9 |
7 |
5 |
3 |
1 |
1/3 |
1/5 |
1/7 |
4-2 |
|
52 |
9 |
7 |
5 |
3 |
1 |
1/3 |
1/5 |
1/7 |
1/9 |
5-2 |
|
42 |
7 |
5 |
3 |
1 |
1/3 |
1/5 |
1/7 |
1/9 |
1/11 |
6-2 |
|
32 |
5 |
3 |
1 |
1/3 |
1/5 |
1/7 |
1/9 |
1/11 |
1/13 |
7-2 |
|
22 |
3 |
1 |
1/3 |
1/5 |
1/7 |
1/9 |
1/11 |
1/13 |
1/15 |
8-2 |
|
12 |
1 |
1/3 |
1/5 |
1/7 |
1/9 |
1/11 |
1/13 |
1/15 |
1/17 |
9-2 |
|
А |
1-2 |
2-2 |
3-2 |
4-2 |
5-2 |
6-2 |
7-2 |
8-2 |
9-2 |
В* |
рис. 16
Напомним любителям строгих формул и определений, что эти "детские
игры" в матрицы имеют самые серьезные последствия.
1. Из физики атома известно, что подоболочки атома характеризуются
следующим структурным составом (протон+электрон).
1,3,5,7,..
Радиусы боровских орбит характеризуются соотношениями
1,4,9,16,...
Удваивая полученные оболочки (это свойство матриц), получаем структуру
Периодической таблицы химических элементов
2,
8, 18, 32,...
2,
8, 18, 32,...
2, 2, 8, 8,18, 18, 32, 32
Не
правда, ли забавные совпадения?
Но эти забавные совпадения окажутся еще забавнее, если мы от этих матриц
перейдем к рассмотрению матриц, взаимодополнительным к данным.
8.
ЧЕТЫРЕХМЕРНОЕ ПРОСТРАНСТВО СЛАВЯНСКИХ МАТРИЦ
Если теперь каждую биномиальную матрицу,
приведенную выше, умножить на золотой ряд, то мы получим золотосеченные матрицы,
построенные по образу и подобию Русской матрицы. По этому данные матрицы по
праву можно называть Славянскими.
Но Славянские матрицы, как,
это было показано выше, представляют собой проекцию на плоскость некоего
кристалла. Свяжем с производящими биномиальными функциями
оси
4-мерной системы координат
XYZ1,
в которой 4-е "единичное"
измерение, отражает "скольжение" 3-мерной системы координат "во времени"
(вперед, или назад ).
 рис. 19
На этой матрице оси системы
координат имеют соответствующий цвет радуги и схематично отражают масштабность.
Видите, как последовательно,
в пространстве 3-х измерений происходит
формирование
новых измерений матрицы.
1=>Z=>
4Y=>2X=>1/2X=>1/4Y=>1/2XZ=>1/1
При переходе в каждое новое измерение базисный вектор нового измерения
оказывается ортогональным к плоскости двух предыдущих векторов, порождая
алгоритм формирования матрицы (каждый текущий вектор равен сумме двух
предшествующих).
Эти
выводы не являются моим изобретением. Они просто подтверждают правоту Д.Мелхиседека, который на страницах книги "Древний Цветок Жизни" неоднократно
обосновывает, что при переходе в новое измерение базисный вектор поворачивается
на угол 90 градусов.
А если
вспомнить, что каждый из нас знает, что такое Декартова система координат, в
которой каждый базисный вектор ортогонален всем остальным.
Но при последовательном
переходе от одно оси координат к другой, у нас встретится только два
случая, когда будет необходимо осуществить переход из "положительной"
системы координат к "отрицательной", и наоборот. Эти точки и
определяют фокус, в котором происходит переворачивание отношений и формированию
обратной пропорции вида
А/1=1/А-1. Причем
эта пропорция трансформируется в равенство только в том единственном случае,
когда они будут являться равноотстоящими от центра симметрии.
Из
рис. 19 непосредственно видно, что переход от оси желтого цвета (2Х) к оси
зеленого цвета (1/2Х) базисный вектор меняет свое направление уже не на 90, а на
180градусов, и базисный вектор из иньского становится янским, порождая взаимодополнительные
измерения Славянской матрицы.
рис. 19
На этой матрице оси системы
координат имеют соответствующий цвет радуги и схематично отражают масштабность.
Видите, как последовательно,
в пространстве 3-х измерений происходит
формирование
новых измерений матрицы.
1=>Z=>
4Y=>2X=>1/2X=>1/4Y=>1/2XZ=>1/1
При переходе в каждое новое измерение базисный вектор нового измерения
оказывается ортогональным к плоскости двух предыдущих векторов, порождая
алгоритм формирования матрицы (каждый текущий вектор равен сумме двух
предшествующих).
Эти
выводы не являются моим изобретением. Они просто подтверждают правоту Д.Мелхиседека, который на страницах книги "Древний Цветок Жизни" неоднократно
обосновывает, что при переходе в новое измерение базисный вектор поворачивается
на угол 90 градусов.
А если
вспомнить, что каждый из нас знает, что такое Декартова система координат, в
которой каждый базисный вектор ортогонален всем остальным.
Но при последовательном
переходе от одно оси координат к другой, у нас встретится только два
случая, когда будет необходимо осуществить переход из "положительной"
системы координат к "отрицательной", и наоборот. Эти точки и
определяют фокус, в котором происходит переворачивание отношений и формированию
обратной пропорции вида
А/1=1/А-1. Причем
эта пропорция трансформируется в равенство только в том единственном случае,
когда они будут являться равноотстоящими от центра симметрии.
Из
рис. 19 непосредственно видно, что переход от оси желтого цвета (2Х) к оси
зеленого цвета (1/2Х) базисный вектор меняет свое направление уже не на 90, а на
180градусов, и базисный вектор из иньского становится янским, порождая взаимодополнительные
измерения Славянской матрицы.
 рис.
20
Посмотрите, Великий Предел матрицы расположен в центре гиперкуба. Кроме того в
эту же точку проектируются 1 и 8 вершины гиперкуба. Видите, какая простая
интерпретация осей Русской и Славянской матрицы?
Данный
рисунок позволяет получить дополнительные представления о тесной взаимосвязи
матрицы И-Цзин, Русской и Славянских матриц с Древним Цветком Жизни.
рис.
20
Посмотрите, Великий Предел матрицы расположен в центре гиперкуба. Кроме того в
эту же точку проектируются 1 и 8 вершины гиперкуба. Видите, какая простая
интерпретация осей Русской и Славянской матрицы?
Данный
рисунок позволяет получить дополнительные представления о тесной взаимосвязи
матрицы И-Цзин, Русской и Славянских матриц с Древним Цветком Жизни.
 рис.
21
Видите, как тесно взаимосвязаны между собой триграммы И-Цзин, Декартова система
координат, Древний Цветок Жизни, арифметический треугольник, степенной бинарный
ряд, степенной биномиальный ряд, Русская и Славянские матрицы?
Только Русская и славянские матрицы отражают в
себе 4-е измерение, отражающее траекторию эволюции куба в гиперкубе. Сектор "-Q"-"Q"
и отражает именно траекторию пути куба в гиперкубе.
Каждая
пара констант из этого сектора является творцом соответствующего "лепестка"
Цветка Жизни, т.е. этот сектор содержит мировые константы Творцов(Эволюция
размерности) собственных Славянских матриц .
Этот
рисунок отражает великое таинство ЕГО ВЕЛИЧЕСТВА ЧИСЛА. Здесь каждая триграмма
(число в восьмеричной системе счисления) отражает смысл всего порождаемого ей
сектора. Эта триграмма является как бы Творцом данного сектора матрицы. Она
является мировой константой (Творцом) более высокого уровня измерения и отражает
смысл того или иного сектора Славянской матрицы, порождаемого биномиальными
степенными функциями.
На странице "Русская
матрица" мы показали, что пара золотосеченных чисел образуют "весы"
рис.
21
Видите, как тесно взаимосвязаны между собой триграммы И-Цзин, Декартова система
координат, Древний Цветок Жизни, арифметический треугольник, степенной бинарный
ряд, степенной биномиальный ряд, Русская и Славянские матрицы?
Только Русская и славянские матрицы отражают в
себе 4-е измерение, отражающее траекторию эволюции куба в гиперкубе. Сектор "-Q"-"Q"
и отражает именно траекторию пути куба в гиперкубе.
Каждая
пара констант из этого сектора является творцом соответствующего "лепестка"
Цветка Жизни, т.е. этот сектор содержит мировые константы Творцов(Эволюция
размерности) собственных Славянских матриц .
Этот
рисунок отражает великое таинство ЕГО ВЕЛИЧЕСТВА ЧИСЛА. Здесь каждая триграмма
(число в восьмеричной системе счисления) отражает смысл всего порождаемого ей
сектора. Эта триграмма является как бы Творцом данного сектора матрицы. Она
является мировой константой (Творцом) более высокого уровня измерения и отражает
смысл того или иного сектора Славянской матрицы, порождаемого биномиальными
степенными функциями.
На странице "Русская
матрица" мы показали, что пара золотосеченных чисел образуют "весы"
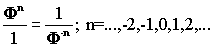 В
Славянской матрице будет справедлива пропорция
В
Славянской матрице будет справедлива пропорция
 т.е. в
Славянской матрице, тек жен как и в Русской для каждого числа существует
его двойник.
Да,
впрочем, иного и нельзя было ожидать. Так велит Единый закон формирования
Славянских матриц. Здесь нет исключения даже для золотых чисел. Наоборот,
золотые числа тесно взаимосвязаны. Что такое золотая пропорция?
Это 1+2/3=Ф1...,
или
1=Ф1-2/3;
Но на страницах сайта мы неоднократно обосновывали, что число 2/3 отражает меру
самодостаточности любого творения, на любом уровне иерархии мироздания.
Поэтому
золотосеченные матрицы отражают самодостаточность всех чисел матрицы
относительно биовертикали Славянских матриц.
Свяжем
теперь с каждой базисной осью производящую функцию этого измерения
1=P0(x)=1/(1+х);
G0(x)=2;
Z=G0(x)=P0(x);
X=G1(x)=G0(x)*2;
Y=G1(x)=G1(x)*2;
-Y=P2(x)/4=G1(x)/4;
-X=G2(x)=P2(x)/2;
-Z=G3(x)=P2(x)/2;
-1=P3(x)=G3(x)*2;
Эти функции отражают Первый
виток спирали, раскручивая которую мы получим пространственную схему
эволюции Славянских матриц.
Теперь,
заменяя оси в цепочке
1=>Z=>
4Y=>2X=>1/2X=>1/4Y=>1/2XZ=>1/1
на
цепочку соответствующих производящих функций (рис.12 )
P0(x)=>G0(x)=>G1(x)=>P1(x)=P2(x)=G2(x)=>G3(x)=>P3(x)
Вот мы
и получили алгоритм, по которому творит свои творения Единый Закон эволюции
двойсвтенного отношения (монады).
Нетрудно понять, что умножив теперь изначальную матрицу (Единичную), содержащую
в себе замысел творения Славянских матриц, мы все последующие Славянские матриц
будем получать золотосеченными.
Второй виток
спирали формируются аналогично, с той лишь разницей, что в качестве исходной производяшей функции здесь выступает уже
P1(x).
На третьем витке исходной
производящей функцией будет
P2(x),
и т.д.
Рассмотренные на страницах сайта свойства производящих функций, свойств
Русской и Славянских матриц, позволяет степенной бинарный ряд вида
...+2-4+2-3+2-2+2-1+20+21+22+23+24+...
порождающий Русскую матрицу, переписать в форме
...+(1+х)-4+(1+х)-3+(1+х)-2+(1+х)-1+(1+х)0+(1+х)1+(1+х)2+(1+х)3+(1+х)4+...
или
...+(1-х)-4+(1-х)-3+(1-х)-2+(1-х)-1+(1-х)0+(1-х)1+(1-х)2+(1-х)3+(1-х)4+..
Но
многомерная Русская матрица порождается рядом
...+2-2(20+21+22+23)+2-1(20+21+22+23)+20(20+21+22+23)+21(20+21+22+23)+22(20+21+22+23)+...
Этот
ряд формирует гиперкуб Русской матрицы.
Используя свойства этого ряда и заменяя удвоенную единицу (2) соответствующим
бинома, мы получаем тот
или иной гиперкуб Славянской матрицы, ту, или иную Периодическую таблицу.
РЕЗЮМЕ
Может быть, мы
снова оказались во влаcти ЕЕ ВЕЛИЧЕСТВА МИСТИКИ?
Действительно, какое отношение имеют
производящие функции к механизму формирования генетического кода?
Мало ли можно придумать математических моделей?
Можно ли
придумать большую чушь, "склеив" в единое целое матрицу И-Цзин,
священный календарь древних майя, Древний Цветок Жизни, священного жука
скарабея, Русскую матрицу, алгоритмы формирования периодической системы
химических элементов, цветов радуги, музыкальных нот.
Разве можно поверить в такую
мистику?
Но весь трагизм
людей, даже имеющих высокие степени учености, а некоторые из них имеют даже
нобелевские отметки, заключается в том, что их мышление нацелено на множественность
моделей мироздания и потому не способно воспринять единство и
целостность мироздания, порождаемого одной и той же моделью -Единым законом
эволюции двойственного отношения.
Поэтому их "здравый смысл" не способен воспринять новое мышление.
И хотя многие из них понимают, что общество уже вошло в стадию глобального
мирового кризиса всех сфер жизнедеятельности, что
человечество находится сегодня в точке бифуркации, в которой решается
судьба планетарного Разума, но не могут осознать, что они
живут ВНЕ ЕДИНОГО ЗАКОНА, что они живут по ПОНЯТИЯМ, а это уже Криминал.
Сегодня
многие видные ученые
уже осознают, что
выход из глобального
системного мирового кризиса возможен только в единственном случае, если человечество
сменит тип мышления.
Новое мышление заключается в том, чтобы
НАЧАТЬ ЖИТЬ по Единому Закону. Тогда и исчезнут угрозы уничтожения и
самоуничтожения.
Но увы,
для ортодоксов, даже тех, кто уже осознает необходимость
нового мышления это все СЛОВА, СЛОВА, СЛОВА,... потому, что их "здравый смысл"
не способен к самоанализу собственного подсознания. Делая выводы о
необходимости нового мышления для других, они
даже в мыслях не позволяют усомниться в "здравом смысле" себя
"любимых".
И потому сегодняшней судьбе людей планеты не позавидуешь. Так, по научному
прогнозу проф. С.П. Капицы уже к 2050 году население планеты уменьшится в
несколько раз. Вдумайтесь, сколько людей уйдут из
жизни за ближайшие 50 лет, сколько людей останется
от 6 млрд. нынешнего? Вдумайтесь, ежегодно из жизни
могут уходить до 100 000 млн. человек!!!
т.е. в
Славянской матрице, тек жен как и в Русской для каждого числа существует
его двойник.
Да,
впрочем, иного и нельзя было ожидать. Так велит Единый закон формирования
Славянских матриц. Здесь нет исключения даже для золотых чисел. Наоборот,
золотые числа тесно взаимосвязаны. Что такое золотая пропорция?
Это 1+2/3=Ф1...,
или
1=Ф1-2/3;
Но на страницах сайта мы неоднократно обосновывали, что число 2/3 отражает меру
самодостаточности любого творения, на любом уровне иерархии мироздания.
Поэтому
золотосеченные матрицы отражают самодостаточность всех чисел матрицы
относительно биовертикали Славянских матриц.
Свяжем
теперь с каждой базисной осью производящую функцию этого измерения
1=P0(x)=1/(1+х);
G0(x)=2;
Z=G0(x)=P0(x);
X=G1(x)=G0(x)*2;
Y=G1(x)=G1(x)*2;
-Y=P2(x)/4=G1(x)/4;
-X=G2(x)=P2(x)/2;
-Z=G3(x)=P2(x)/2;
-1=P3(x)=G3(x)*2;
Эти функции отражают Первый
виток спирали, раскручивая которую мы получим пространственную схему
эволюции Славянских матриц.
Теперь,
заменяя оси в цепочке
1=>Z=>
4Y=>2X=>1/2X=>1/4Y=>1/2XZ=>1/1
на
цепочку соответствующих производящих функций (рис.12 )
P0(x)=>G0(x)=>G1(x)=>P1(x)=P2(x)=G2(x)=>G3(x)=>P3(x)
Вот мы
и получили алгоритм, по которому творит свои творения Единый Закон эволюции
двойсвтенного отношения (монады).
Нетрудно понять, что умножив теперь изначальную матрицу (Единичную), содержащую
в себе замысел творения Славянских матриц, мы все последующие Славянские матриц
будем получать золотосеченными.
Второй виток
спирали формируются аналогично, с той лишь разницей, что в качестве исходной производяшей функции здесь выступает уже
P1(x).
На третьем витке исходной
производящей функцией будет
P2(x),
и т.д.
Рассмотренные на страницах сайта свойства производящих функций, свойств
Русской и Славянских матриц, позволяет степенной бинарный ряд вида
...+2-4+2-3+2-2+2-1+20+21+22+23+24+...
порождающий Русскую матрицу, переписать в форме
...+(1+х)-4+(1+х)-3+(1+х)-2+(1+х)-1+(1+х)0+(1+х)1+(1+х)2+(1+х)3+(1+х)4+...
или
...+(1-х)-4+(1-х)-3+(1-х)-2+(1-х)-1+(1-х)0+(1-х)1+(1-х)2+(1-х)3+(1-х)4+..
Но
многомерная Русская матрица порождается рядом
...+2-2(20+21+22+23)+2-1(20+21+22+23)+20(20+21+22+23)+21(20+21+22+23)+22(20+21+22+23)+...
Этот
ряд формирует гиперкуб Русской матрицы.
Используя свойства этого ряда и заменяя удвоенную единицу (2) соответствующим
бинома, мы получаем тот
или иной гиперкуб Славянской матрицы, ту, или иную Периодическую таблицу.
РЕЗЮМЕ
Может быть, мы
снова оказались во влаcти ЕЕ ВЕЛИЧЕСТВА МИСТИКИ?
Действительно, какое отношение имеют
производящие функции к механизму формирования генетического кода?
Мало ли можно придумать математических моделей?
Можно ли
придумать большую чушь, "склеив" в единое целое матрицу И-Цзин,
священный календарь древних майя, Древний Цветок Жизни, священного жука
скарабея, Русскую матрицу, алгоритмы формирования периодической системы
химических элементов, цветов радуги, музыкальных нот.
Разве можно поверить в такую
мистику?
Но весь трагизм
людей, даже имеющих высокие степени учености, а некоторые из них имеют даже
нобелевские отметки, заключается в том, что их мышление нацелено на множественность
моделей мироздания и потому не способно воспринять единство и
целостность мироздания, порождаемого одной и той же моделью -Единым законом
эволюции двойственного отношения.
Поэтому их "здравый смысл" не способен воспринять новое мышление.
И хотя многие из них понимают, что общество уже вошло в стадию глобального
мирового кризиса всех сфер жизнедеятельности, что
человечество находится сегодня в точке бифуркации, в которой решается
судьба планетарного Разума, но не могут осознать, что они
живут ВНЕ ЕДИНОГО ЗАКОНА, что они живут по ПОНЯТИЯМ, а это уже Криминал.
Сегодня
многие видные ученые
уже осознают, что
выход из глобального
системного мирового кризиса возможен только в единственном случае, если человечество
сменит тип мышления.
Новое мышление заключается в том, чтобы
НАЧАТЬ ЖИТЬ по Единому Закону. Тогда и исчезнут угрозы уничтожения и
самоуничтожения.
Но увы,
для ортодоксов, даже тех, кто уже осознает необходимость
нового мышления это все СЛОВА, СЛОВА, СЛОВА,... потому, что их "здравый смысл"
не способен к самоанализу собственного подсознания. Делая выводы о
необходимости нового мышления для других, они
даже в мыслях не позволяют усомниться в "здравом смысле" себя
"любимых".
И потому сегодняшней судьбе людей планеты не позавидуешь. Так, по научному
прогнозу проф. С.П. Капицы уже к 2050 году население планеты уменьшится в
несколько раз. Вдумайтесь, сколько людей уйдут из
жизни за ближайшие 50 лет, сколько людей останется
от 6 млрд. нынешнего? Вдумайтесь, ежегодно из жизни
могут уходить до 100 000 млн. человек!!!
|

 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©