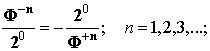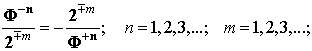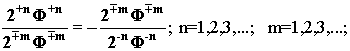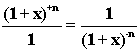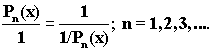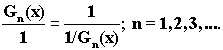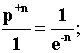Славянская матрица-1

Славянская матрица-1

"Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг).

М.И. Беляев, 2015г,©

СЛАВЯНСКИЕ МАТРИЦЫ

1. СЛАВЯНСКИЕ МАТРИЦЫ

Русская матрица порождается двумя производящими функциями, -бинарной и золотосеченной, свойства которых были рассмотрены выше.

Однако всеобщность свойств чисел Русской матрицы должно проявляться не только в свойствах бинарной и золотосеченной производящей функции.

Это означает, что существуют и другие взаимодополнительные производящие функции, способные порождать Русские матрицы.

Поэтому далее особый класс Русских матриц, порождаемых взаимодополнительными биномиальными производящими функциями, будем называть Славянскими матрицами.

Свойства биномиальных производящих функций достаточно подробно обоснованы на странице "Преемственность".

1.1. БИНОМ НЬЮТОНА И РУССКАЯ МАТРИЦА

Всеобщность золотого ряда ни у кого не вызывает сомнения, как и тот факт, что золотое сечение тесно взаимосвязано с рядом Фибоначчи. В различных справочниках приводятся сотни формул, связывающих ряд Фибоначчи с золотым сечением, в том числе и ряд формул, отражающих взаимодействия в мире элементарных частиц [92]. Среди этих формул хочется отметить одну- бином Ньютона для золотой пропорции, порождающий Единицу

где -число перестановок.

В результате мы получаем Единичную диагональ Русской матрицы

А бином Ньютона, как известно, отражает степенную функцию двойственного отношения.

Данная формула привязывает бином золотого отношения к Единичной диагонали Русской матрицы, определяемой золотой пропорцией

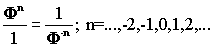Видите, как тесно взаимосвязаны Единица, золотой египетский ряд и бином Ньютона?

Если теперь каждый столбец Русской матрицы разделить на соответствующий член золотого ряда, то мы получим бинарный степенной ряд

.... +2⁵+2⁴+2³+2²+2¹+2⁰+2^-1+2^-2+2^-3+2^-4+2^-5+.....

из которого и складывается Русская матрица, используя этот ряд, совместно с золотым рядом, в виде произведений 2^±n Ф^±^m, по вертикали и по горизонтали.

В	2⁸	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰	A^*
2⁸	2⁺⁸Ф^-4	2⁺⁷Ф^-3	2⁺⁶Ф^-2	2⁺⁵Ф^-1	2⁺⁴Ф⁰	2⁺³Ф⁺¹	2⁺²Ф⁺²	2⁺¹Ф⁺³	2⁰Ф⁺⁴	2⁰
2⁷	2⁺⁷Ф^-4	2⁺⁶Ф^-³	2⁺⁵Ф^-2	2⁺⁴Ф^-1	2⁺³Ф⁰	2⁺²Ф⁺¹	2^±nФ⁺²	2⁰Ф⁺³	2^-1Ф⁺⁴	2^-1
2⁶	2⁺⁶Ф^-4	2⁺⁵Ф^-3	2⁴Ф^-2	2⁺³Ф^-1	2⁺²Ф⁰	2⁺¹Ф⁺¹	2⁰Ф⁺²	2^-1Ф⁺³	2^-2Ф⁺⁴	2^-2
2⁵	2⁺⁵Ф^-4	2⁺⁴Ф^-3	2⁺³Ф^-2	2²Ф^-1	2⁺¹Ф⁰	2⁰Ф⁺¹	2^-1Ф⁺²	2^-2Ф⁺³	2^-3Ф⁺⁴	2^-3
2⁴	2⁺⁴Ф^-4	2⁺³Ф^-3	2⁺²Ф^-2	2⁺¹Ф^-1	2⁰Ф⁰	2^-1Ф⁺¹	2^-2Ф⁺²	2^-3Ф⁺³	2^-4Ф⁺⁴	2^-4
2³	2⁺³Ф^-4	2⁺²Ф^-3	2⁺¹Ф^-2	2⁰Ф^-1	2^-1Ф⁰	2^-2Ф⁺¹	2^-3Ф⁺²	2^-4Ф⁺³	2^-5Ф⁺⁴	2^-5
2²	2⁺²Ф^-4	2⁺¹Ф^-3	2⁰Ф^-2	2^-1Ф^-1	2^-2Ф⁰	2^-3Ф⁺¹	2^-⁴Ф⁺²	2^-5Ф⁺³	2^-6Ф⁺⁴	2^-6
2¹	2⁺¹Ф^-4	2⁰Ф^-3	2^-1Ф^-2	2^-2Ф^-1	2^-3Ф⁰	2^-4Ф⁺¹	2^-5Ф⁺²	2^-6Ф⁺³	2^-7Ф⁺⁴	2^-7
2⁰	2⁰Ф^-4	2^-1Ф^-3	2^-2Ф^-2	2^-3Ф^-1	2^-4Ф⁰	2^-5Ф⁺¹	2^-6Ф⁺²	2^-7Ф⁺³	2^-8Ф⁺⁴	2^-8
A	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	В^*

рис. 1

Главная диагональ Русской матрицы формируется золотым тождеством

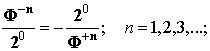Нетрудно увидеть, что любая побочная диагональ, формируется тождеством

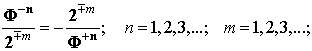При отрицательных значениях m будут формироваться диагонали Русской матрицы, лежащие ниже главной, при положительных значениях будут формироваться диагонали, лежащие над главной диагональю.

Если теперь этому тождеству сопоставить взаимодополнительное тождество

и затем совместить его с первым, то мы получим новое тождество

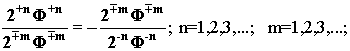В этом тождестве главная диагональ Русской матрицы уже изначально смещена, а взаимодополнительная диагональ уже определяет над- и под- диагонали матрицы.

Это тождество является более общим, ибо оно отражает ориентацию Единичного центра Русской матрицы относительно ее абсолютного центра.

В центре Русской матрицы располагается системообразующая матрица-энеаграмма.

4	2	1		2²	2¹	2⁰
2	1	1/2	Û	2¹	2⁰	2¹
1	1/2	1/4		2⁰	2^-1	2^-2

Это Куб, в центре которого размещается девятая вершина -Великий Предел Куба. Этот куб является системообразующим. Из него, по образу и подобию, рождается вся Русская матрица. Поэтому данный "кубик"-матрицу мы будем называть базисным.

Если каждый столбец матрицы (рис. 8) поделить на соответствующий член золотого ряда

Ф^-⁴

Ф^-3

Ф^-2

Ф^-1

Ф⁰

Ф¹

Ф²

Ф³

Ф⁴

где Ф¹=1,618, мы получим Русскую первоматрицу.

В	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	A^*
2⁸	256	128	64	32	16	8	4	2	1	2⁰
2⁷	128	64	32	16	8	4	2	1	1/2	2^-1
2⁶	64	32	16	8	4	2	1	1/2	1/4	2^-2
2⁵	32	16	8	4	2	1	1/2	1/4	1/8	2^-3
С	16	8	4	2	1	1/2	1/4	1/8	1/16	С^*
2³	8	4	2	1	1/2	1/4	1/8	1/16	1/32	2^-5
2²	4	2	1	1/2	1/4	1/8	1/16	1/32	1/64	2^-6
2¹	2	1	1/2	1/4	1/8	1/16	1/32	1/64	1/128	2^-7
2⁰	1	1/2	1/4	1/8	1/16	1/32	1/64	1/128	1/256	2^-8
A	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	В^*

рис. 2

Видите обратную пропорцию чисел в секторах Русской матрицы: АС/С^*А^*?

Заметим также, что сектора CB =1/ C^*B^*являются удвоенными, а сектора АС и 1/С^*А^* состоят из двух взаимодополнительных половинок. При этом диагональ ВВ^* является учетверенной.

Отметим, что бинарный ряд

1,2,4,8,16,32,...

формируется диагоналями следующей матрицы.

В	2⁰	2¹	2²	2³	8	2⁵	2⁶	2⁷	2⁸	A^*
2⁰	1	1	1	1	1	1	1	1	1	2^-⁸
2¹	1	2	3	4	5	6	7	1	1/1	2^-⁷
2²	1	3	6	10	18	24	1	1/7	1/1	2^-⁶
2³	1	4	10	20	38	1	1/24	1/6	1/1	2^-⁵
С	1	5	18	38	1	1/38	1/18	1/5	1/1	С^*
2⁵	1	6	24	1	1/38	1/20	1/10	1/4	1/1	2^-³
2⁶	1	7	1	1/24	1/18	1/10	1/6	1/3	1/1	2^-²
2⁷	1	1	1/7	1/6	1/5	1/4	1/3	1/2	1/1	2¹
2⁸	1	1/1	1/1	1/1	1/1	1/1	1/1	1/1	1/1	2⁰
A	2^-⁸	2^-⁷	2^-⁶	2^-⁵	A^*	2^-³	2^-²	2^-1	2⁰	В^*

рис. 3

Нетрудно понять, что эта матрица является арифметическим треугольником.

Сложение столбцов (или строк) матрицы порождает ряды вида

P₀(x)=1,1,1,1,1,1,...

P₁(x)=1,2,3,4,5,6,7,...

P₂(x)=1,3,6,10,...

P₃(x)=1,4,10,20,...

Все сектора данной матрицы взаимосвязаны друг с другом инвариантными преобразованиями.

1.2. ВЕСЫ ПРОИЗВОДЯЩИХ ФУНКЦИЙ

Резонансные отношения характеризуют инвариантные переходы в матрице из одного состояния в другое, используя весы матрицы

рис. 4

Это тождество возникает только тогда когда между полюсами монады будет существовать баланс "спроса" и "предложения" вида

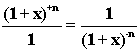Посмотрите, какие отношения гармонии существуют между Образом и его Подобием в каждом полюсе монады? И точно такие же рыночные гармонические взаимоотношения существуют и между полюсами монады. Точно такие же отношения существуют и между взаимодополнительнымии монадами, в которых монады уже являются взаимодополнительными полюсами.

И такие рыночные отношения формируются, по образу и подобию, во всей Вселенной.

Применительно к производящим функциям это тожество можно записать в следующем виде

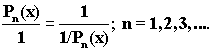
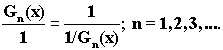Эти тождества характеризуются законом сохранения зарядовой симметрии, в соответствии с принципами самоорганизации (Cамоорганизация). Необходимо отметить, что учет закона сохранения зеркальной симметрии приведет к тому, что правая и левая части тождеств будут иметь разные знаки.

И если в какой-то момент в монаде возникают возмущения, то возникает Сила саморегуляции, которая формирует баланс "спроса" и "предложения на новом уровне, расталкивая или приталкивая полюса монады.

Наиболее ярким примером гармоничных рыночных отношений является Периодическая система химических элементов, в которой каждый химический элемент "живет" свято соблюдая баланс рыночных отношений между протонными и электронными оболочками.

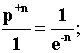Осознайте великую гармонию этих резонансных взаимодействий. В каждом атоме, с порядковым номером n, между протонными и электронными подоболочками и оболочками существует баланс взаимоотношений. И пока такой баланс существует, атом химического элемента обладает стабильностью.

Видите, какой "массивный" протон, а ведь он может управляться "маленьким" электроном. Помните закон рычага - "выигрываешь в силе- проигрываешь в расстоянии". В протоне собственный внутренний радиус невелик, а масса, по сравнению с электроном велика. В электроне же наоборот. У него радиус вращения большой, а масса невелика. Поэтому в результате возникающих возмущений не только протон может управлять электроном, но и электрон может влиять на состояние протона, до такой степени. что электрон может "переродиться" в протон. Это конечно гипотеза, которую можно отнести к разряду фантастических, но весы монады химических элементов, отражающие единство сущностного и функционального такую возможность допускают.

А теперь постарайтесь ответить себе на вопрос - являются ли рыночными те отношения в мировой экономике, которые всемерно внедряются на всех уровнях бытия современного человечества?

Разве можно назвать отношениями гармонии не стремление к гармоничному развитию, а стремлениями к навязывающим другим (производителям, потребителям, партнерам, странам и государствам) своей воли?

1.3. БИНОМИАЛЬНЫЕ СЛАВЯНСКИЕ МАТРИЦЫ

Рассмотренные выше свойства Русской матрицы, в основе которой лежит бинарный ряд вида

.... +2⁵+2⁴+2³+2²+2¹+2⁰+2^-1+2^-2+2^-3+2^-4+2^-5+.....

легко обобщается до биномиальной Славянской матрицы, в основе которой лежит биномиальный ряд вида

.... +(1 ± x)⁵+(1 ± x)⁴+(1 ± x)³+(1 ± x)²+(1 ± x)¹+(1 ± x)⁰+(1 ± x)^-1+(1 ± x)^-2+(1 ± x)^-3+(1 ± x)^-4+(1 ± x)^-5+.....

Если условно положить, что "2" есть монада с внутренней двойственностью, т.е. ее внутренняя структура с точки зрения наблюдателя неразличима, то бином является уже монадой с внешней двойственностью, т.е. формально мы получили тоже степенной бинарный ряд, но это бинарный ряд сформирован монадой с внешней двойственностью.

Подобные обобщения позволяет формировать более сложные Славянские матрицы, в которых

отношения между диагоналями будет отражаться тождественными отношениями между производящими функциями вида

В Русской матрице ровно 8 секторов. Может быть, Русская матрица является проекцией на плоскость Цветка Жизни, в котором каждый сектор является лепестком, и может сворачиваться в Великий Предел -Единицу?

В центре Русской матрицы мы видим Единицу -Великий Предел Матрицы, а ближайшие к ней Единицы образуют двойной Единичный крест, составленный из Великих Пределов секторов матрицы.

Распишем теперь матрицу в следующем виде.

рис. 5

Два "матричных креста" порождают новый свастичный крест, состоящий из 8 секторов

(4-целочисленных + 4 дробных) и все они формируются из исходного ряда с использованием степенного биномиального ряда.

Обратите внимание, в соответствии с законами сохранения свастичного креста, в каждом из них существует цепочка инвариантных преобразований С->P->C*->P*->. В первом кресте эта цепочка "вращается" по часовой стрелке, а во второй -против часовой стрелки. Складываясь вместе, с противоположными "спинами", мы получаем схему формирования многоуровневых бинарных степенных рядов Славянской матрицы.

рис. 6

Умножая треугольные матрицы вида [х_0,х_1,х_2,х₃] и умножая его на степенной бинарный

вектор-столбец вида [2⁰,2¹,2²,2³] , получим

2^-2[х_0,х_1,х_2,х₃]+2^-1[х_0,х_1,х_2,х₃] +2⁰[х_0,х_1,х_2,х₃]+2¹[х_0,х_1,х_2,х₃]+2²[х_0,х_1,х_2,х₃]+2³[х_0,х_1,х_2,х₃]+..

мы получим гиперкуб славянской матрицы.

Если связать с инвариантными преобразованиями вида РС и Р^*С^* операторы транспонирования треугольной матрицы (А^Т), а с оператором С^*Р^*-оператор формирования обратной треугольной матрицы (1/А^Т), то мы увидим поистине фантастическую гармонию инвариантных преобразований.

На каждой стороне матрицы есть два одноименных, но взаимопротивоположных инвариантных преобразования. Они являются зеркальным отображением друг друга. Но при переходе с одной стороны на другую такой симметрии уже нет. Здесь происходит зеркальное копирование в ортогональную плоскость.

Но при этом каждое преобразование переводит треугольную матрицу в новое измерение в соответствии с законами инвариантных преобразований.

Многомерность инвариантных преобразований С->P->C*->P*->... , реализуемых одним и тем же механизмом, позволяет получать и более сложные Славянские матрицы.

рис. 7

Видите, здесь из четырех матриц формируется новая матрица более высокого уровня измерения.

Здесь в каждом свастичном секторе мы будем иметь уже свертку соответствующей матрицы в треугольную. Далее начинаются процессы формирования взаимодополнительного свастичного креста и слияние их в новую матрицу, и т.д.

Каждую матрицу, имеющих по восемь секторов можно отождествить с Кубом, а матрица следующего уровня измерения будет располагаться в "лепестках" гиперкуба.

Таким образом, мы приходим к осознанию тесной связи Русской матрицы с

биномиальными производящими функциями (Преемственность), Единым законом эволюции двойственного отношения и Древним Цветком Жизни (Эзотерика).

Полагая Pⁿ=Pⁿ(x)=(1 ± x)ⁿ, n=.....-2,-1,0,1,2,3,4,...., мы по образу и подобию с Русской матрицей, получим следующую биномиальную Славянскую первоматрицу.

В	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	A^*
	P⁸	P⁷	P⁶	P⁵	P⁴	P³	P²	P¹	P⁰
	P⁷	P⁶	P⁵	P⁴	P³	P²	P¹	P⁰	P^-1
	P⁶	P⁵	P⁴	P³	P²	P¹	P⁰	P^-1	P^-2
	P⁵	P⁴	P³	P²	P¹	P⁰	P^-1	P^-2	P^-3
С	P⁴	P³	P²	P¹	P⁰	P^-1	P^-2	P^-3	P^-4	С^*
	P³	P²	P¹	P⁰	P^-1	P^-2	P^-3	P^-4	P^-5
	P²	P¹	P⁰	P^-1	P^-2	P^-3	P^-2	P^-3	P^-4
	P¹	P⁰	P^-1	P^-2	P^-3	P^-4	P^-5	P^-6	P^-7
	P⁰	P^-1	P^-2	P^-3	P^-4	P^-5	P^-6	P^-7	P^-8
A	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	В^*

рис. 8

Умножая столбцы и строки полученной матрицы на соответствующие члены золотого египетского ряда,

... ,Ф^-4,Ф^-3,Ф^-2,Ф^-1,Ф⁰,Ф¹,Ф²,Ф³,Ф⁴,..., где Ф¹=1, 618....,

мы получим гармонизированную биномиальную Славянскую матрицу, в которой взаимоотношения между двумя взаимодополнительными полюсами характеризуются золотой пропорцией.

Вот, собственно, мы и получили матрицу, лежащую в основе масштабной гармонии Вселенной.

По аналогии со Славянской матрицей, порождаемой биномиальными производящими функциями

.... +(P(x))⁵+(P(x))⁴+(P(x))³+(P(x))²+(P(x))¹+(P(x))⁰+(P(x))^-1+(P(x))^-2+(P(x))^-3+(P(x))^-4+(P(x))^-5+.....

можно получить Славянскую матрицу, порождаемую биномиальными производящими функциями вида

.... +(G(x))⁵+(G(x))⁴+(G(x))³+(G(x))²+(G(x))¹+(G(x))⁰+(G(x))^-1+(G(x))^-2+(G(x))^-3+(G(x))^-4+(G(x))^-5+.....

где G_i(x)=P_i(x)(1 ± x)⁺¹

Соответствие между функциями устанавливается по следующим правилам.

Функция (1-х)^±n умножается на (1 - x)⁺¹, а функция (1+х)^±n умножается на (1 + x)⁺¹.

В	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	A^*
	G⁸	G⁷	G⁶	G⁵	G⁴	G³	G²	G¹	G⁰
	G⁷	G⁶	G⁵	G⁴	G³	G²	G¹	G⁰	G^-1
	G⁶	G⁵	G⁴	G³	G²	G¹	G⁰	G^-1	G^-2
	G⁵	G⁴	G³	G²	G¹	G⁰	G^-1	G^-2	G^-3
С	G⁴	G³	G²	G¹	G⁰	G^-1	G^-2	G^-3	G^-4	С^*
	G³	G²	G¹	G⁰	G^-1	G^-2	G^-3	G^-4	G^-5
	G²	G¹	G⁰	G^-1	G^-2	G^-3	G^-2	G^-3	G^-4
	G¹	G⁰	G^-1	G^-2	G^-3	G^-4	G^-5	G^-6	G^-7
	G⁰	G^-1	G^-2	G^-3	G^-4	G^-5	G^-6	G^-7	G^-8
A	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	В^*

рис. 9

Видите, структура матрицы нисколько не изменилась. Но данная матрица отражают уже другое измерение Славянских матриц. Умножение матрицы (рис.16-1) на оператор (1 ± x)⁺¹ приводит к удвоению матрицы ( а деление на этот оператор приводит к раздвоению матрицы).

Другими словами, бесконечномерная биномиальная матрица рис. 18-1 нормируется и становится единичной и при умножении такой свернутой в точку матрицы порождается матрица рис. 9, в которой каждая клетка является вселенной, сформированной биномиальной Славянской матрицей более низкого измерения.

Подобная многоуровневость формирования Славянских матриц, по образу и подобию, отражается в масштабной гармонии Вселенной, в универсальности алгоритма формирования рыночных отношений во Вселенной.

В любой Славянской матрице любого уровня измерения, как и в Русской матрице, существуют 2 взаимодополнительные пары чисел, или соответствующих производящих функций, взаимоотношения которых характеризуются резонансными взаимодействиями, отражающими баланс двойственных отношений.

2. СЕМЕЙСТВА СЛАВЯНСКИХ МАТРИЦ

2.1. СЛАВЯНСКИЕ СВАСТИКИ

Свастика (вращающийся крест), являющаяся символом Знаний Рода Древних - славян, история которых уходит вглубь веков не менее чем на 100 000 лет. Так об этом повествуется в Ведах.

рис. 10

Но, оказывается, что существуют и Праведы. Этот источник знаний был открыт учеными Международной Академии Меганауки (г. Петрозаводск) и в настоящее время этот труд опубликован [134] ("ПРАВЕДЫ. Древнее Священное Знание северных волхвов", ЗАО "Международная академия меганауки", "Белые альвы", 2015г.). "Многолепестковость" свастичных символов позволяет рассмотреть проблему их происхождения с позиций природных операционных механизмов Единого закона эволюции двойственного отношения. О. Макеев в своей книге "Око Возрождения-Дыхание Земли. Постижение внутренней стороны йоги" (Омск, ГУИПП "Омский дом печати", 2015) приводит следующий рисунок, который демонстрирует взаимосвязь свастики с Древним Цветком Жизни и с Русской матрицей.

рис. 11

На этих рисунках, кроме "четырехлепесткового" свастичного символа, используются трехлепестковые и шестилепестковые свастичные символы.

Эти рисунки еще ждут своих исследователей. Сейчас отметим только некоторые наиболее важные свойства этих рисунков. Я обращаю внимание читателей на слово "трехлепестковые". Наш мир отражает свойства двулучевой свастики (двойные спиральные галактики и т.д.). В нашем мире нет трехлучевых галактик. Откуда у древних славян знания о том, что существуют галактики с иными свойствами эволюционных потоков ЯН-ИНЬ?

Далее, существующие "круги на полях" (О космологии) представляют прямые свидетельства о существовании трехлепестковых миров.

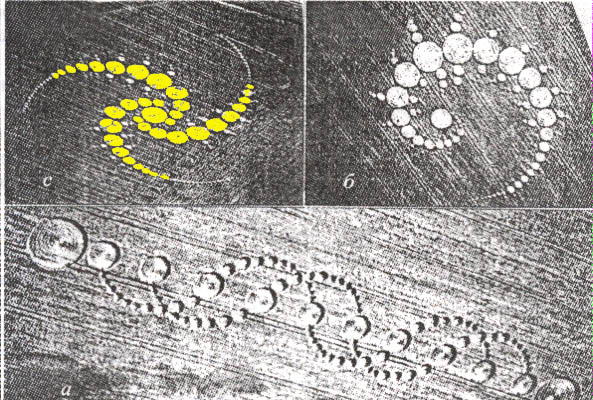рис. 12

Эти рисунки позволяют осознать "многолепестковость" нашего мироздания и "многолепестковость" Русской матрицы, которую по праву следует называть Славянской матрицей.

Может быть, трехлепестковая Славянская матрица будет иметь следующий вид?

В	3⁸	3⁷	3⁶	3⁵	3⁴	3³	3²	3¹	3⁰	A^*
3⁸	3⁺⁸Ф^-4	3⁺⁷Ф^-3	3⁺⁶Ф^-2	3⁺⁵Ф^-1	3⁺⁴Ф⁰	3⁺³Ф⁺¹	3⁺²Ф⁺²	3⁺¹Ф⁺³	3⁰Ф⁺⁴	3⁰
3⁷	3⁺⁷Ф^-4	3⁺⁶Ф^-³	3⁺⁵Ф^-2	3⁺⁴Ф^-1	3⁺³Ф⁰	3⁺²Ф⁺¹	3^±nФ⁺²	3⁰Ф⁺³	3^-1Ф⁺⁴	3^-1
3⁶	3⁺⁶Ф^-4	3⁺⁵Ф^-3	3⁴Ф^-2	3⁺³Ф^-1	3⁺²Ф⁰	3⁺¹Ф⁺¹	3⁰Ф⁺²	3^-1Ф⁺³	3^-2Ф⁺⁴	3^-2
3⁵	3⁺⁵Ф^-4	3⁺⁴Ф^-3	3⁺³Ф^-2	3²Ф^-1	3⁺¹Ф⁰	3⁰Ф⁺¹	3^-1Ф⁺²	3^-2Ф⁺³	3^-3Ф⁺⁴	3^-3
3⁴	3⁺⁴Ф^-4	3⁺³Ф^-3	3⁺²Ф^-2	3⁺¹Ф^-1	3⁰Ф⁰	3^-1Ф⁺¹	3^-2Ф⁺²	3^-3Ф⁺³	3^-4Ф⁺⁴	3^-4
3³	3⁺³Ф^-4	3⁺²Ф^-3	3⁺¹Ф^-2	3⁰Ф^-1	3^-1Ф⁰	3^-2Ф⁺¹	3^-3Ф⁺²	3^-4Ф⁺³	3^-5Ф⁺⁴	3^-5
3²	3⁺²Ф^-4	3⁺¹Ф^-3	3⁰Ф^-2	3^-1Ф^-1	3^-2Ф⁰	3^-3Ф⁺¹	3^-⁴Ф⁺²	3^-5Ф⁺³	3^-6Ф⁺⁴	3^-6
3¹	3⁺¹Ф^-4	3⁰Ф^-3	3^-1Ф^-2	3^-2Ф^-1	3^-3Ф⁰	3^-4Ф⁺¹	3^-5Ф⁺²	3^-6Ф⁺³	3^-7Ф⁺⁴	3^-7
3⁰	3⁰Ф^-4	3^-1Ф^-3	3^-2Ф^-2	3^-3Ф^-1	3^-4Ф⁰	3^-5Ф⁺¹	3^-6Ф⁺²	3^-7Ф⁺³	3^-8Ф⁺⁴	3^-8
A	Ф^-⁴	Ф^-3	Ф^-2	Ф^-1	Ф⁰	Ф¹	Ф²	Ф³	Ф⁴	В^*

рис. 13

Рассмотрим триадные взаимоотношения в "базисном кубике", из которого для простоты рассмотрния удалены "золотые числа"

3²	3⁺¹	3⁰
3⁺¹	3⁰	3^-1
3⁰	3^-1	3^-2

Прежде всего, необходимо предположить, что центральная трехлепестковая ветка должна лежать на диагонали этой матрицы. Все ветви этой трехлепестковой свастики нормированы (единичные).

Теперь мы можем выделить в этой базисной матрице остальные трехлепестковые ветки.

Из этих тождеств видно, что две взаимодополнительные ветки, сопряжены с противоположными "зарядами", а третья ветка формирует центральную удвоенную ветвь, как бы демонстрируя собственную триграммность (самодостаточность). Она будет "управлять" вращением двух других " трехлепестковых веток"

Этот базисный "кубик" , составленный из трехлепестковых спиралей показывает, что и далее этот "кубик" будет разворачивать в триграммые лепестки, порождая триграммную Славянскую матрицу.

Рисунок 11 отражает многомерность Славянских триграммых матриц.

Так, на рисунке выше приведена следующая свастика

Эта свастика в качестве базисного тождества содержит четырехлепестковую свастику. Эволюцию этой свастики можно описать следующей схемой.

рис. 14

Данная схема отражает сущность разворачивания "базисной матрицы" из Великого предела (Числа), отражающего баланс взаимоотношений четырех "непроявленых сил". "Проявленной" оказывается только базисная матрица размерностью 3х3. В совокупности формируются 13 вершин "хроматической гаммы" Славянской матрицы (8 белых, проявленных клавиш и 5 черных, непроявленных).

2.2. СЕМЕЙСТВО ДУАДНЫХ СЛАВЯНСКИХ МАТРИЦ

Приведенный выше рисунок позволяет более глубоко осознать взаимосвязь двухлепестковых и трехлепестковых спиралей. Двухлепестковые спирали (рисунок слева) формируют Славянскую матрицу матрицу, которая обладает "мезонными" свойствами, (по аналогии с соответствующим мезонным семейством элементарных частиц).

Каждое число в этих семействах порождается весами (клеточной матрицей) вида, имеющих две перекладины

Это "семейство" Славянских матриц порождает гиперкубическое "пространство-время", свойство которой достаточно убедительно описывается Славянской матрицей "пространства-времени".

В	T^-⁴	T^-3	T^-2	T^-1	T⁰	T¹	T²	T³	T⁴	A^*
L⁸	T^-⁴L⁸	T^-3L⁷	T^-2L⁶	T^-1L⁵	T⁰L⁴	T¹L³	T²L²	T³L¹	T⁴L⁰	L⁰
L⁷	T^-⁴L⁷	T^-3L⁶	T^-2L⁵	T^-1L⁴	T⁰L³	T¹L²	T²L¹	T³L⁰	T⁴L^-1	L^-1
L⁶	T^-⁴L⁶	T^-3L⁵	T^-2L⁴	T^-1L³	T⁰L²	T¹L¹	T²L⁰	T³L^-1	T⁴L^-2	L^-2
L⁵	T^-⁴L⁵	T^-3L⁴	T^-2L³	T^-1L²	T⁰L¹	T¹L⁰	T²L^-1	T³L^-2	T⁴L^-3	L^-3
L⁴	T^-⁴L⁴	T^-3L³	T^-2L²	T^-1L¹	T⁰L⁰	T¹L^-1	T²L^-2	T³L^-3	T⁴L^-4	L^-4
L³	T^-⁴L³	T^-3L²	T^-2L¹	T^-1L⁰	T⁰L^-1	T¹L^-2	T²L^-3	T³L^-4	T⁴L^-5	L^-5
L²	T^-⁴L²	T^-3L¹	T^-2L⁰	T^-1L^-1	T⁰L^-2	T¹L^-3	T²L^-4	T³L^-5	T⁴L^-6	L^-6
L¹	T^-⁴L¹	T^-3L⁰	T^-2L^-1	T^-1L^-2	T⁰L^-3	T¹L^-4	T²L^-5	T³L^-6	T⁴L^-7	L^-7
L⁰	T^-⁴L⁰	T^-3L^-1	T^-2L^-2	T^-1L^-3	T⁰L^-4	T¹L^-5	T²L^-6	T³L^-7	T⁴L^-8	L^-8
A	T^-⁴	T^-3	T^-2L^-³	T^-1	T⁰	T¹	T²	T³	T⁴	В^*

Эта матрица имеет размерность 9х9 и содержит в себе "золотой крест" Великих пределов, порождающих все числа этой Славянской матрицы на всех уровнях Мироздания. Эта матрица порождает гипер-Платоново тело - гиперкуб.

Обозначая базисные весы символами G,U,C, A и возводя матрицу в последовательные степени, мы получим последовательно следующие тензорные матрицы, отражающие свойства соответствующих тензорных подпространств гиперкуба.

рис. 15

Данная матрица представляет собой проекцию гиперкуба на плоскость. По этой единственной проекции, используя законы взаимодополнительности чисел Русской матрицы, можно построить многомерный гиперкуб.

рис. 16

Каждая число этого гиперкуба представляет собой генетический код, из которого формируется матрица ДНК. Великий предел этого гиперкуба (центр рисунка) является "главной осью", вокруг которой вращаются все "кубики".

2.3. СЕМЕЙСТВО ТРИАДНЫХ СЛАВЯНСКИХ МАТРИЦ

Свастичный рисунок 15 (справа) порождает семейство Славянских матриц, каждое число которых является трехлепестковым".

Нетрудно видеть, что базисная матрица этого семейства состоит из 13 чисел. И эта базисная матрица порождает уже "барионное" семейство Русских матриц. Каждое число в этих матрицах обладает "барионными"свойствами ( по аналогии со свойствами соответствующего барионного семейства элементарных частиц, т.е. здесь "Замысел" каждого числа Славянской матрицы отражает ее "трехлепестковость (триединство). Обозначая "лепестки" Русских матриц через G, U, C, A_, мы получим значение каждого числа, отражающего триединство Замысла его творения.

На странице "Спиноры и тензоры" приведена следующая матрица, отражающая свойства этой трехлепестковой матрицы.

рис. 17

Эта матрица характеризует свойства Мирозданий, порожденных базисным "барионным семейством Славянских матриц. Нетрудно увидеть, что данная матрица формирует новый базисный куб мироздания, в которой каждая вершина куба формируется из 4-х базисных матричных весов.

2.4. СОВЕРШЕННОЕ СЕМЕЙСТВО СЛАВЯНСКИХ МАТРИЦ

Свойства приведенных выше семейств Славянских матриц позволяет осознать взаимосвязь этих семейств с классификацией Платоновых тел.

рис. 18

Из этой схемы видно, что должно существовать еще семейство Славянских матриц, которое отражается тензорной матрицей гипердодекаэдра.

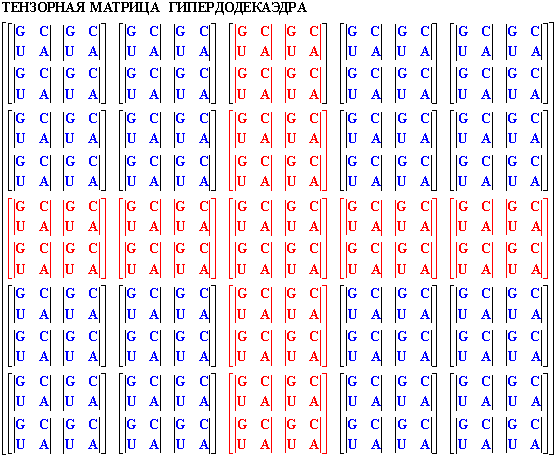рис. 19

Эта матрица имеет размерность 20х20 и содержит 400 чисел. Крест этой матрицы, как и крест матрицы гиперикосаэдра, соткан из базисных весов Мироздания гиперкуба.

Сравнивая структуру полученной матрицы со структурой матрицы гиперкуба (рис.15), мы отчетливо видим, что матрица гипердодекаэдра соткана из 4-х (!) матриц гиперкуба.

При этом "крест" матрицы гипердодекаэдра также формирован из базисных сегментов, которые являются "первокирпичиками" всех трех гиперматриц (гиперкуба, гиперикосаэдра, гипердодекаэдра).

3. ЖИВЫЕ И НЕЖИВЫЕ СЕМЕЙСТВА СЛАВЯНСКИХ МАТРИЦ

3.1.ОПРЕДЕЛЕНИЕ СУЩНОСТИ ЖИВОГО

Приведенные выше свойства семейств позволяют осознать принципиальную разницу между живым и неживым. Интуитивно, на уровне подсознания, все мы понимаем, что есть живое, а что неживое. Однако дать точное определение жизни весьма непросто. Современная биология при описании живого идет по пути перечисления основных свойств живых организмов. При этом неизменно подчеркивается, что только совокупность данных свойств может дать представление о специфике жизни.

К числу свойств живого обычно относят следующие.

- Живые организмы характеризуются сложной, упорядоченной структурой. Уровень их организации значительно выше, чем в неживых системах.

- Живые организмы получают энергию из окружающей среды, используя ее на поддержание своей высокой упорядоченности. Большая часть организмов прямо или косвенно использует солнечную энергию.

- Живые организмы активно реагируют на окружающую среду. Если толкнуть камень, то он пассивно сдвигается с места. Если толкнуть животное, оно отреагирует активно: убежит, нападет или изменит форму.

-Способность реагировать на внешние раздражения - универсальное свойство всех живых существ, как растений, так и животных.

- Живые организмы не только изменяются, но и усложняются. Так, у растения или животного появляются новые ветви или новые органы, отличающиеся по своему химическому составу от породивших их структур.

- Все живое размножается. Эта способность к самовоспроизведению, пожалуй, самая поразительная способность живых организмов. Причем потомство и похоже, и в то же время чем-то отличается от родителей. В этом проявляется действие механизмов наследственности и изменчивости, определяющих эволюцию всех видов живой природы.

- Сходство потомства с родителями обусловлено еще одной замечательной особенностью живых организмов - передавать потомкам заложенную в них информацию, необходимую для жизни, развития и размножения. Эта информация содержится в генах - единицах наследственности, мельчайших внутриклеточных структурах.

Генетический материал определяет направление развития организма. Вот почему потомки похожи на родителей. Однако эта информация в процессе передачи несколько видоизменяется, искажается. В связи с этим потомки не только похожи на родителей, но и отличаются от них.

-- Живые организмы хорошо приспособлены к среде обитания и соответствуют своему образу жизни. Строение крота, рыбы, лягушки, дождевого червя полностью соответствует условиям, в которых они живут.

Несколько упрощая сказанное о специфике живого, можно отметить, что все живые организмы питаются, дышат, растут, размножаются и распространяются в природе, а неживые тела не питаются, не дышат, не растут и не размножаются.

Наконец, существует следующее обобщенное представление о сущности живого: жизнь есть форма существования сложных, открытых систем, способных к самоорганизации и самовоспроизведению. Важнейшими функциональными веществами этих систем являются белки и нуклеиновые кислоты.

3.2. ЖИВЫЕ И НЕЖИВЫЕ ГИПЕРМАТРИЦЫ

И все же совокупность признаков живого и неживого является неполной. Она не отражает некоторых самых существенных отличий живого и неживого.

Свойства приведенных выше гиперматриц позволяют осознать некоторые важнейшие свойства, по которым можно отличить живое от неживого.

Так, приведенный на рисунке 16 гиперкуб является "неживым". Он не содержит в себе "животворящего креста" , который формируется из Великих пределов "кубиков" и Великого предела Гиперкуба.

Для того, чтобы превратить этот гиперкуб в живой необходимо в каждый "кубик" вложить "Замысел" его творения. Может быть теперь ученым станет ясна роль вырожденных генетических кодонов, которых насчитывается ровно 17.

Расмотрим свойства Русской матрицы, изображенная на рис. 13. Здесь в явном виде присутствует "золотой крест", несущий Замысел творения всех чисел Русской матрицы и расчленяющих ее на четыре сегмента, которые по отношению друг к другу являются взаимодополнительными, т.е. формируют многомерные базисные весы Русской матрицы, которые используются затем в качестве "чипов", при формировании гиперматриц более высокого уровня. Но эти базисные "чипы", не являются "живыми", ибо они не имеют собственного "золотого креста" Великих пределов, которые позволяют им разворачиваться в пространстве и сворачиваться в двумерное, одномерное и нульмерное пространство.

Если каждому базисному "чипу" сопоставить собственный "золотой крест" Великих пределов, то мы получим живую систему, которая способна не только к разворачиванию в многомерное гиперпространство живого, но и к сворачиванию в нуль-мерное пространство (Великий предел гиперматрицы живого).

В этом смысле все приведенные выше Славянские гиперматрицы являются "неживыми". Это неживые кристаллы, которые могут быть совершенными, но неживыми. Они могут разворачиваться из Великого предела (золотого креста кристалла), но уже не могут "дышать" и не могут сворачиваться в Великий предел. На это способна только живая материя.

И хотя граница между неживым и живым в современной науке становится все призрачней, видимо можно сказать, что живое характеризуется наличием у той или иной структуры собственной гиперматрицы, имеющей собственный глобальный "золотой крест", при этом каждый базисный "чип" этой гиперматрицы также имеет собственный "локальный" "золотой крестик".

Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать о всех замеченных ошибках, некорректных формулировках.

Книги "Основы милогии", "Милогия" могут быть высланы в Ваш адрес наложенным платежом,

URL1: milogy.net

e-mail: [email protected]

Карта сайта

rss

Карта