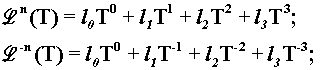ОСНОВЫ ТЕОРИИ ИЕРАРХИИ
Основы теории
иерархии приведены в монографии "Милогия"[2]. Здесь
приводится только самые необходимые представления о свойствах многоуровневых
пространств.
1. СОБСТВЕННЫЕ ПРОСТРАНСТВА
1.1. О СОБСТВЕННЫХ ИЕРАРХИЧЕСКИХ
ПРОСТРАНСТВАХ
Собственные иерархические пространства и
их свойства также достаточно подробно описаны в
[2]. Для понимания сути собственных
пространств приведем некоторые самые
простые трактовки, описанные в [2].
Иерархические пространства -это
упорядоченная последовательность
вложенных друг в друга, или
пересекающихся друг с другом пространств.
особое значение имеют собственные
иерархические пространства, т.к. они
являются всеобщим инвариантом, всеобщей
категорией, используя которую, можно
осуществлять взаимнооднозначные переходы
из одного собственного пространства в
другое. Подобные переходы из одного
собственного пространства в другое, из
одного измерения в другое, из одного
устойчивого состояния в другое, в рамках милогии носят название фазовых переходов.
Инвариантность является самой важной
отличительно чертой всех физических
законов. В самом простом случае
инвариантность двух объектов ( структур,
явлений, ...) означает, что между ними
существует симметрия относительно тех
или иных преобразований. Поэтому понятие
инвариантности по праву лежит в
основе всех математических методов,
использующих взаимнооднозначные
преобразования математических объектов.
Но
собственные пространства в новой науке обладают некоторыми особыми свойствами,
благодаря которым все остальные виды и типы пространств становятся частными
случаями собственных пространств.
Обычно всегда, когда говорят, например, о пространстве-времени, то
подразумевают 3-х мерное геометрическое пространство, а в качестве 4-го
измерения считают временную координату.
Здесь все несколько иначе. Любое
собственное пространство формируется двойственным отношением (монадой). Свойства
Великого
Предела двойственного отношения позволяет
определить одно из важных свойств собственных пространств - их свертку и
развертку, с понижением, или повышением мерности собственного пространства.
Далее, в собственном
пространстве смысл измерений определяет само двойственное отношение. Если
измерения двойственного отношения будут иметь геометрический смысл, то мы
получим геометрический смысл пространства. Время в собственных пространствах
является сугубо относительным понятием. т.е. время не является четвертым
измерением пространства -времени. Время не является первым измерением этого
пространства. Оно является просто одним из измерений собственного пространства.
И это измерение может быть свернуто, или развернуто. В зависимости от этого
собственное пространство может иметь параметр время, а может его и не иметь. В
этом собственном пространстве ВРЕМЯ может быть и не одномерным, если монада
будет характеризовать эволюцию ВРЕМЕНИ, как такового, когда возникает
необходимость проанализировать ЦВЕТОК ВЕЛИКОГО ПРЕДЕЛА ВРЕМЕНИ.
1.2. О СОБСТВЕННЫХ ИНЕРЦИАЛЬНЫХ СИСТЕМАХ
ОТСЧЕТА
Из школьного курса физики известно о
существовании инерциальных систем отсчета.
Такие инерциальные системы отсчета
связываются в физике с движущимися
объектами и используются для определения
относительных скоростей движения одной
инерциальной системы относительно другой.
Но подобные инерциальные системы ничего не
говорят о том, какие силы заставляют
двигаться с той или иной скоростью ту
или иную инерциальную систему. Они не
говорят о масштабности явлений,
происходящих "внутри" инерциальных
систем. Собственные инерциальные системы
являются естественным обобщением
инерциальных систем. Так, связывая с
каждой инерциальной системой некоторый
набор собственных значений, мы можем
получить возможность осуществлять фазовые
переходы из одного собственного
инерциального пространства в другое. На рис.1
изображены две собственные
инерциальные системы отсчета. В центре
системы отсчета размещены скалярные и
векторные величины, характеризующие
набор собственных значений данной системы
отсчета. Этот набор определяет подобие
данной системы другим, ориентацию ее
осей, ее "вес", масштаб ее
пространственных измерений. и т.д.

Рис.1
Зная собственные значения движущихся
собственных инерциальных систем отсчета,
можно получить возможность инвариантных
переходов из одной движущейся
собственной инерциальной системы отсчета в
другую. Следует отметить, что расчет
параметров фазового перехода далеко не
всегда может быть реализован, например,
из-за возможных негативных последствий. Так,
пассажир на полном ходу курьерского
поезда не рискнет выйти из него, т.д.
Изображенные на рис. 1 собственные
инерциальные системы отсчета в самом общем
случае не предполагают физического
движения друг относительно друга. Они
отражают взаимосвязь их собственных
значений. И в этом их важное отличие от
тривиальных инерциальных систем отсчета.
Так, например, в данной собственной
системе отсчета между собственными
значениями существуют взаимнооднозначные
инвариантные преобразования (рис. 2).
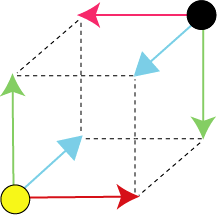
рис.
2
Нетрудно видеть, что мы получим систему
квадр, в которой две собственные
инерциальные системы движутся навстречу
друг другу. Аналогичные
результаты мы получим
и для собственных систем отсчета, удаляющихся друг от друга.
Теперь можно обобщить вышеизложенное.
Можно сказать, что любое собственное
пространство характеризуется двойственной
парой собственных инерциальных систем
отсчета, связанных с движением как
собственного пространства, так и с
движением друг относительно друга.
Рассмотрим теперь некоторые свойства
монадных семейств с позиций собственных
пространств. Любое рассмотренное монадное
семейство можно отождествить с собственным
пространством. Так, систему координат любой
монады, мы
получим прямоугольную систему координат,
относительно осей которых и будет
осуществляться движение собственных
инерциальных систем отсчета относительно
общего центра, создавая основу для взаимных
инвариантных преобразований. Любое
изменение любого собственного значения
переводит собственную инерциальную
систему координат в новое "измерение".
Таких измерений в прямоугольной систем
координат восемь. И они взаимосвязаны
двойственными отношениями, порождаемые
двойственной парой движущейся монады
("свет-тьма"). В этом случае
взаимоотношения между вершинами
исходной монады могут заменяться их
проекциями на оси координат.

рис.
3
Данная схема может характеризовать
отношения между двумя собственными
пространствами как отношения с внешней
двойственностью. В этой схеме два тетраэдра
являются зеркальным отображением друг
друга, не взаимопроникая друг в друга. Такое
собственное пространство можно
воспринимать как два собственных
подпространства, с противоположным "спином"
(зеркальностью).
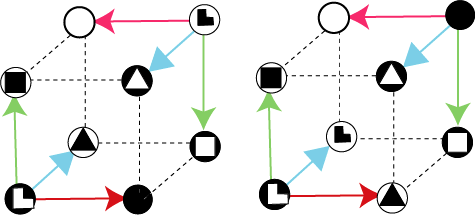
рис.
4
Выше, при
анализе типов монадных семейств (подробнее),
были подробно описаны свойства приведенных
на рисунке монадных форм. Поэтому
отметим только особенности. Здесь каждая
одноцветная вершина связана с тремя
разноименными вершинами, каждая из
которых имеет другой цвет.
Разница между левым и правыми рисунками
заключается в способах сопряжения
вершин.
Следующие рисунки описывает
случай взаимоотношения связанных
собственных инерциальных систем отсчета и
потому такие двойственные отношения
могут характеризоваться как отношения с
внутренней двойственностью. Здесь мы имеем
одно собственное пространство,
характеризуемого внутренней симметрией
инвариантных преобразований.

рис.
5
Левый рисунок характеризует дуадные
взаимоотношения между вершинами
собственных инерциальных систем отсчета,
при которых каждая вершина соединена с
тремя другими, отличающимися от нее по
цвету, создавая, таким образом,
бесцветную вершину. Эти формы обладают
удивительной симметрией. Диаметрально
противоположные вершины на любой грани
куба являются одноцветными, а
лежащие на любой грани - разноцветные.
При этом все одноцветные вершины на
диагоналях грани являются взаимодополнительными друг к другу,
образуя как бы одно измерение, а две взаимно
перпендикулярные диагонали любого
квадрата - характеризуют животворящий
крест, с его функциональным
механизмом инвариантных
преобразований при переходе с одной "перекладины"
на другую. Естественно, если двойственные
отношения в такой системе будут не
сбалансированы, то собственные
инерциальные системы, объединенные в
звездный тетраэдр, начнут движение друг
относительно друга. Можно говорить о том,
что в таком собственном пространстве любые
две вершины являются диаметрально
противоположны друг к другу.
На правом рисунке взаимоотношения между
движущимися собственными инерциальными
системами отсчета претерпевают
существенные отличия. Здесь царит другой
тип отношений. Здесь любая квадра
формируется за счет последовательно-параллельного соединения. Две одноименные
вершины соединяются последовательно,
третья, ортогональная к двум первым, характеризует переход к новому
измерению.
Введение понятий собственных инерциальных
систем отсчета, собственных пространств,
может показаться несколько искусственным
приемом. В математике, механике,
физике и т.д., существует
множество изящных методов решения
подобных задач. Однако рассмотренный
подход может иметь свои преимущества.
Поскольку все двойственные отношения в
такой системе взаимосвязаны, каждое
отношение в равновесной системе
характеризуется собственным законом
сохранения, то любое изменение значения
любой вершины монадной формы немедленно
приведет к автоматическому пересчету
значений всех других вершин монадной формы.
Поэтому данная модель собственных
пространств, в основе которой лежат законы
сохранения двойственных отношений,
безусловно, является перспективным.
Поэтому Природа так стремится к
созданию совершенных симметричных форм.
Эти формы позволяют восстанавливать (регенерировать)
даже "утерянные" двойственные
отношения.
1.3. О ПРИРОДНЫХ ПЕРЕНОРМИРОВОЧНЫХ МЕХАНИЗМАХ
И КОЭФФИЦИЕНТАХ ПОДОБИЯ СОБСТВЕННЫХ ПРОСТРАНСТВ.
Законы сохранения
двойственных отношений в любом
собственном пространстве еще не
позволяют использовать осуществлять
инвариантных преобразований при фазовых
переходах из одного собственного
пространства в другое. Поэтому
Природа такой вопрос решает тривиально
просто. Каждое собственное пространство
нормируется и все операции преобразования
выполняются над относительными величинами.
Однако каждое нормированное
пространство имеет свой собственный "вес"
(или "массу"), которые будет
использованы при переходе к абсолютным
единицам измерения. Принимая абсолютную
"массу" собственного пространства за 1
и осуществляя пересчет всех
остальных значений в относительных
единицах, мы получаем возможность
оценить подобие сравниваемых собственных
пространств и получить эффективную
оценку их параметров, вычислив
коэффициенты подобия. Зная эти
коэффициенты, задача инвариантных
фазовых переходов из одного собственного
пространства в другое становится
тривиальной.
Механизм перенормировок, в условиях многоуровневого вложения одних
собственных пространств в другие, позволяет эффективно использовать механизм
инвариантных преобразований собственных пространств, превращая их в
формальную и тривиальную задачу, независимо от уровня иерархии собственных
пространств.
В
основе природных механизмов
перенормировки лежит функциональный
механизм животворящего креста, описанию
которого на сайте уделено
достаточно много внимания (подробнее).
1.4. ПОСТУЛАТЫ МНОГОМЕРНОСТИ
СОБСТВЕННЫХ ПРОСТРАНСТВ.
Постулат 0. Любая
система n-мерного измерения
при переходе в новое измерение (большей, или меньшей размерности), изменяет
ориентацию всех своих базисных векторов (n-го
измерения) на 900. При этом
базисный вектор
(n+1)-го измерения
оказывается ортогональным базисному
вектору n-го измерения.
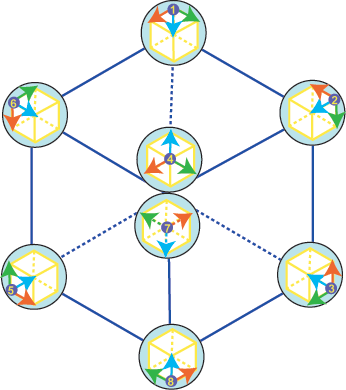
Из данного рисунка видно, что в 3-х
мерном векторе в каждой вершине куба все его базисные орты ортогональны
одноименным ортам из соседних вершин. Связывая с каждой вершиной куба
базисный вектор высшего измерения (очевидно, что если 1-й вершине куба
приписать размерность 3, то высшая размерность 8-й
вершины характеризоваться числом 3+7=10), мы придем к следующим
следствиям.
Следствие 1. Все
базисные векторы собственных пространств являются центростремительными.
Поэтому базисный вектор
любого собственного пространства будем в дальнейшем называть
вектором устремления этого
пространства.
Следствие
2.
Каждое локальное
собственное пространство (вершина куба) является четырехмерным (тетраэдр).
Чтобы
убедиться в этом, о достаточно соединить между собой концы всех базисных
векторов той или иной вершины куба.
Следствие
3.
Из вершины базисного
вектора собственного пространства высшего измерения, -(n+1)
-й мерности, видно все собственное пространство с меньшей мерностью (n-й
мерности).
Например, из вершины тетраэдра,
которая является базисным вектором 4-го измерения (локального) видны все три
базисные векторы, лежащие в основании тетраэдра.
Другие постулаты
многомерности пространств обоснованы в книге Ю.А. Фомина "Энциклопедия
аномальных явлений", М.,1993г:
Постулат 1.
Любая система высшего измерения может содержать бесчисленное множество
независимо существующих систем низшего измерения (на плоскости можно
разместить сколь угодно много линий, в объеме - сколь угодно много плоскостей,
n-мерная система может содержать в себе сколь
угодно (n-1)-мерных систем).
Постулат 2.
Всякое понятие о
расстояниях справедливо только в данной системе измерений. При переходе
к высшим системам измерений расстояние между двумя любыми точками может
быть сведено к нулю, или бесконечно малой величине.
Пример. Расстояние между
точками А и B на плоскости может быть сведено к
нулю при сворачивании в кольцо (или изгибе) части плоскости (лента).
Постулат 3.
Любые пространственные системы могут быть
искривлены без какой-либо деформации, только в высших системах измерения. Причем
эта деформация может быть обнаружена только в высшей системе измерений и не
проявляться в низшей.
Постулат 4.
Физические тела могут проявляться в разных системах
измерения, причем чем ниже система измерения, тем меньший объем информации она
несет. Сложные объекты проявляются в низших измерениях в виде следов,
проекций и сечений.
Постулат 5.
Чем выше мерность системы, тем большей
информационной сложностью она обладает.
Постулат 6.
Система низшего измерения
любого порядка в высших измерениях может сворачиваться в точку без нарушения ее
целостности, при этом все точки низшей системы сохраняя свое взаимное
расположение, оказываются совмещенными.
Но эти постулаты Ю.А. Фомина
не являются полными. Они не учитывают ограниченность и
замкнутость собственных пространств и свойства Великого Предела двойственных
отношений.
Пример 1. Сворачивая плоскость в трубочку, мы перейдем к
3-мерному пространству, но сжимая диаметр трубочки (сворачивание трубочки в
спираль) до бесконечности, мы получим свернутое одномерное пространство
(линия). Сворачивание "трубочки" в кольцо, снова приводит к повышению
размерности, но сворачивание трубочки в спираль с бесконечно малым радиусом
кривизны снова приводит к дальнейшему уменьшению мерности пространства до 1
(точка).
Этот пример приводит к необходимости введения
еще одного постулата.
Постулат 7.
При
достижении высшей мерности измерений происходит последовательная свертка высшей
системы измерений в низшую, т.е. трехмерная система измерений сворачивается в
одномерную систему измерений, с сохранением набора собственных значений,
характеризующих свойства свернутого собственного пространства.
Этот постулат
характеризует свойство самонормирования собственных пространств. Любое
собственное пространство с позиции внешнего наблюдателя является нормированным
(единичным). С точки зрения теории информации (Информация)
это точка представляет собой бит.
Мерность внутренней
структуры "бита информации" на одно измерение меньше. Так, если собственное
пространство порождается двумерным собственным пространством, то новое
измерение вновь рожденного собственного пространства, будет
являться единичным
вектором устремления собственного пространства.
И потому предыдущее собственное пространство
сворачивается в единичную точку, характеризуя внутреннюю структуру свернутого
пространства.
Любой
вектор устремления в
собственном пространстве может быть свернут в скаляр (собственное значение
собственного пространства). Разворачивание собственного значения в собственный
вектор устремления производится путем умножения этого собственного
значения (скаляра) на соответствующий единичный вектор устремления.
Примечание.
При нормировании собственного пространства его собственное значение, отличное
от единичного, трансформируется в дробное число (доля от единицы).
Поэтому в общем случае, единичный вектор будут
характеризоваться произведением собственного значения
с на единичный вектор
х
нормированного собственного пространства,
т.е. с*
х.
Понятно, что данный постулат является двойственным. Характеризуя свойства
сворачивания собственного пространства в Великий Предел, он допускает обратное
преобразование -Великого Предела в многомерное собственное пространство -по
образу и подобию. Поэтому при обратном преобразовании мы должны использовать уже
собственное значение, равное
1/С.
Эти постулаты
характеризуют важные свойства собственных пространств. Отметим главные:
1. Мерность собственных пространств не
превышает числа 3.
Почему мерность собственных пространств не
превышает числа 3?
Во-первых, Единый закон эволюции двойственного
отношения (монады) проявлен для куба, геометрическая структура которого
является трехмерной.
Во-вторых,
из свойств монадных семейств мы видим, что все "частицы" таких семейств
порождаются двумя или тремя одномерными "частицами"(точками соответствующих
собственных пространств.
2. Собственные пространства являются
ограниченными и замкнутыми.
Эти свойства непосредственно вытекают из
постулатов Ю.А. Фомина.
3.
Ограниченность и замкнутость собственных
пространств порождает их оболочечное строение (структуру и функции).
3. Всякий раз, когда мерность собственного
пространства оказывается более трех, происходит сворачивание собственных
пространств в пространство меньшей мерности (перенормировка собственных значений
пространства). Это частный случай замыкания (сворачивание в единичную
оболочку) собственного пространства (в точку).
4. Собственные пространства обладают свойствами
инвариантности, т.е. собственные пространства характеризуются симметрией
относительно тех или иных преобразований, например, множество инвариантных
собственных пространств можно записать в виде цепочки, связанной
взаимнооднозначными преобразованиями вида
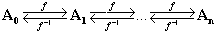
Данная цепочка собственных пространств может быть
характеризоваться как система вложенных друг в друг собственных пространств. Эти
пространства непосредственно не соединены друг с другом. Поэтому в определенной
степени их можно считать пространствами с параллельным соединением.
Соответственно можно определить и собственные пространства с последовательным
соединением.
Если в такой
цепочке ( с параллельным, либо последовательным соединением) на каком-либо этапе
эволюции происходит сворачивание собственного пространства (постулат
7), то обратное преобразование приведет к
разворачиванию этого собственного пространства.
2. СТРУКТУРНО-ФУНКЦИОНАЛЬНЫЙ ДУАЛИЗМ СИСТЕМ
Теория систем
кибернетика, как наука о саморегулировании двойственных отношений в
системах самых различной природы, синергетика, как наука о самоорганизации,
порядок и беспорядок, всесторонне отражают концепцию системного подхода
и несут в себе множество самых "точных" определений и системных понятий.
Среди них встречается и такое простое определение:
"Порядок- это определенное расположение
элементов в пространстве или их последовательность во времени".
Именно это простенькое
определение несет в себе глубочайший смысл единства СТРУКТУРЫ И ФУНКЦИИ.
Это единство можно
характеризовать как "структурно-функциональный дуализм". Этот дуализм
проявляется в том, что в одних случаях свойства системы могут
рассматриваться с позиций структурного аспекта, в то время
как в других случаях система рассматривается с позиций функционального
аспекта.
Этот подход в
определенной мере является аналогом корпускулярно-волнового дуализма, ибо свет
также является системой, которая может проявляться как структура (корпускула)
или как функция (волна).
Похожесть принципов структурно-функционального дуализма и
корпускулярно-волнового дуализма позволяет более глубоко понять и природу
такого феномена, как принцип неопределенности Гейзенберга в физике микромира.
В классической механике состояние материальной точки (классической частицы)
определяется заданием значений координат, импульса, энергии и т.д.
Но информация о микрочастицах может быть получена путем наблюдения их
взаимодействия с приборами, представляющими собой макроскопические тела.
Поэтому результаты измерений, естественно, выражаются в терминах,
разработанных для характеристики макротел а затем таким образом
измеренные
значения приписываются микрочастицам.
Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных
получаются при измерениях определенные значения. Так, например, электрон (и
любая другая микрочастица) не может иметь одновременно точные значения
координаты
х
и импульса
р.
Неопределенности координат и импульса удовлетворяют соотношению В. Гейзенберга
(1927):
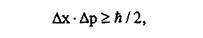 где
где
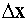 и и 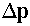 -
неопределенности значений
х
и р,
являющиеся среднеквадратичными отклонениями.
Этот принцип утверждает, что если частица локализована в пространстве со
среднеквадратичным отклонением -
неопределенности значений
х
и р,
являющиеся среднеквадратичными отклонениями.
Этот принцип утверждает, что если частица локализована в пространстве со
среднеквадратичным отклонением
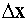 ,
то ее импульс может принимать значения, находящиеся в пределах «ширины» ,
то ее импульс может принимать значения, находящиеся в пределах «ширины»
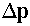 .
Физический смысл принципа неопределенности состоит в том, что невозможно
одновременно определить значения координаты и импульса частицы.
В физике микромира имеются и другие соотношения, аналогичные вышеприведенному,
например, для энергии и времени .
Физический смысл принципа неопределенности состоит в том, что невозможно
одновременно определить значения координаты и импульса частицы.
В физике микромира имеются и другие соотношения, аналогичные вышеприведенному,
например, для энергии и времени
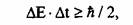
Это соотношение означает, что
определение энергии с заданной
точностью в данный момент времени должно занять определенный интервал,
определяемый данным выражением.
Соотношения неопределенности указывают, в какой мере можно
пользоваться понятиями классической механики применительно к микрочастицам.
Отметим, что подобные соотношения будут справедливы и для соотношений координат
частиц и их скоростью

т.е. чем
больше масса частицы, тем меньше неопределенность ее координаты и скорости, и,
следовательно, с тем большей точностью применимо понятие траектории.
Похожесть принципов структурно-функционального дуализма и
корпускулярно-волнового дуализма позволят сделать предположение и о том,
что подобная аналогия имеет место и для соотношений принципа
неопределенности., т.е. применительно к системах такой принцип может означать,
что в каждый момент времени мы не можем мгновенно и точно определить
одновременно структуру и функцию системы. Рассматривая функцию (процесс), мы
фиксируем только фрагмент структуры, задействованный для реализации этой
функции. Рассматривая целостную структуру, мы не можем сказать, какие
функции существуют и реализуются в системе "здесь и сейчас", во всех ее
фрагментах.
Структурно-функциональный дуализм систем и принцип неопределенности,
вытекающий из него, может свидетельствовать о том, что
мнение принадлежности принципа неопределенности только к физике микромира
очень сильно преувеличено, что этот принцип характеризует более
фундаментальную природу двойственного отношения "структура-функция".
3. ВЕЛИКИЙ ПРЕДЕЛ И
СТРУКТУРНО-ФУНКЦИОНАЛЬНЫЙ ДУАЛИЗМ
Природа структурно-функционального принципа организации материи и
духа отражается в ВЕЛИКОМ ПРЕДЕЛЕ двойственного
отношения (Универсальный закон). "Прошлое"
системы отражается в ВЕЛИКОМ ПРЕДЕЛЕ как функция, а "Будущее" - как структура,
порожденная ВЕЛИКИМ ПРЕДЕЛОМ.
Сам же
Великий Предел -"это миг между Прошлым и Будущим", связывающим в единое целое
прошлое и будущее, характеризующим целостность системы на любом этапе ее
эволюции и порождающий структурно-функциональный аспект.
ВЕЛИКИЙ
ПРЕДЕЛ-это единство Ян и Инь (Книга перемен).
 рис.
6
В физике микромира
каждая элементарная частица является неделимой, и потому может считаться
ВЕЛИКИМ ПРЕДЕЛОМ - результатом слияния с последующим самонормированием
синтезируемых элементарных частиц. Здесь корпускулярно-волновой дуализм
несет в себе только функциональный аспект и отражает в себе
информацию о своем Прошлом. В физике микромира эту функциональную информацию
несут кварки -виртуальные частицы с дробным зарядом.
Каким образом эта информация
сохраняется в частицах? Каждая частица имеет
собственные "вибрации", собственную волновую функцию.
В 1924 г. выдающийся
французский физик Луи де Бройль выдвинул смелую гипотезу о том, что
двойственность имеет универсальное значение.
По де Бройлю, движение электрона или какой-либо другой частицы связано с
волновым процессом, характеризующимся длиной волны,
которая связана с
импульсом частицы
р
соотношением
рис.
6
В физике микромира
каждая элементарная частица является неделимой, и потому может считаться
ВЕЛИКИМ ПРЕДЕЛОМ - результатом слияния с последующим самонормированием
синтезируемых элементарных частиц. Здесь корпускулярно-волновой дуализм
несет в себе только функциональный аспект и отражает в себе
информацию о своем Прошлом. В физике микромира эту функциональную информацию
несут кварки -виртуальные частицы с дробным зарядом.
Каким образом эта информация
сохраняется в частицах? Каждая частица имеет
собственные "вибрации", собственную волновую функцию.
В 1924 г. выдающийся
французский физик Луи де Бройль выдвинул смелую гипотезу о том, что
двойственность имеет универсальное значение.
По де Бройлю, движение электрона или какой-либо другой частицы связано с
волновым процессом, характеризующимся длиной волны,
которая связана с
импульсом частицы
р
соотношением

Здесь h
— постоянная Планка.
Эта формула показывает, что волновая функция содержит в себе информацию о
собственном числе "частиц", замкнувшихся в новую более сложную частицу,
т.е. самонормирование волновой функции имеет место только тогда, когда
сформируется новый коэффициент, характеризующий число "частиц", породивших
данную.
Таким образом, функция
элементарной частицы представляет собой волновую голограмму, несущую
информацию о структуре.
Вспомним, что в
биноме Ньютона число членов в каждом многочлене степени n
равно n, а последовательность коэффициентов в
получаемых многочленах образует арифметические ряды, известные как треугольник
Паскаля .
(1+х)n=
1+.......+xn-1
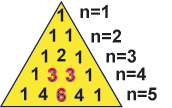
Эти коэффициенты характеризуются замечательно
простым алгоритмом их получения. Каждый коэффициент в нижележащем многочлене
является суммой коэффициентов, расположенных над ним, например, 3+3=6, 1+3=4, и
т.д.
Рассмотрим, для примера, следующую производящую функцию
(1-х)2=1-2х+х2.
В этой функции три члена (триединство). Если
в этой функции пронормировать коэффициенты, то мы получим
3((1/3) -
(2/3)х +(1/3)х2)
Не напоминает ли
набор коэффициентов (1/3 -2/3 +1/3)
свойства кварков - виртуальных частиц физики
микромира, из которых сложены большинство семейств
элементарных частиц?
Производящая функция обладает генной памятью.
Она позволяет, зная коэффициенты производящей функции, восстановить исходную
структуру, т.е. процесс восстановления исходного двучлена (монады) в нашем
случае однозначен. Процесс возрождения закончится, когда число членов
производящей функции будет равно двум (монада с внешней двойственностью), или
одному (монада с внутренней двойственностью).
4. ФРАКТАЛЫ И ПРОИЗВОДЯЩИЕ ФУНКЦИИ
Понятие фрактал (от
лат. fraktus — расколотый, раздробленный, состоящий из фрагментов)
Мандельброт использовал для обозначения нерегулярных,
но самоподобных структур. Позднее Мандельброт дал такое определение фрактала: «Фракталом
называется структура, состоящая из частей, которые в каком-то смысле подобны
целому».
В 1979 году Мандельброт
обнаружил, что простейшие
нелинейные фракталы задаются квадратичными функциями,
в виде:
Zn+1
->
Z 2n
+ С
Стрелка
(->) означает итерацию.
Стоит отметить, что по простоте предпосылки и богатству
следствий и смыслов алгоритм Мандельброта
Z
->
Z2
+ С сравним с гениальной теоремой Пифагора а2 + b2 = с2
или с уникальной формулой Эйнштейна E = mс2.
И это не преувеличение. На странице "О
хаосе"
приведено обоснование для использования
производящих функций вида (1-х)n для
порождения элементарных частиц.
В биноме Ньютона
число членов в каждом многочлене степени
n
равно
n, а последовательность коэффициентов в
получаемых многочленах образует арифметические ряды, известные как треугольник
Паскаля .
(1-х)n=
1-.......+xn-1

рис. 7
На этом рисунке приведен треугольник
Паскаля, в котором каждый член является биномиальным коэффициентом. При этом
строки (столбцы) и диагонали матрицы сформированы разными производящими
функциями. Строки (столбы) -функцией вида (1-х)-n,
а диагонали матрицы-функцией вида (1-х)х.
На странице "Преемственность"
мы рассматривали свойства производящих функций
Gn(x)=Pn(x)(1-x)
где
P1(x)=(1+x)-1=1-x+x2-x3+
...
P2(x)=(1+x)-2=1-2x+3x2-4x3+...
P3(x)=(1+x)-3=1-3x+6x2-10x3+...
P4(x)=(1+x)-4=1-5x+14x2-30x3+...
 рис. 8
На
страницах сайта мы показали связь этих функций с формированием подоболочек
и оболочек Периодической системы химических элементов.
Отметим некоторые важнейшие свойства этих
функций.
Биномиальные коэффициенты характеризуются
замечательными свойствами.
1.
Характеризуются замечательно
простым алгоритмом их получения. Каждый коэффициент в нижележащем многочлене
является суммой коэффициентов, расположенных над ним, например, 3+3=6, 1+3=4, и
т.д.
2. В
этом треугольнике в каждой производящей функции первый и последний
коэффициент равен единице.
3. Сумма коэффициентов в каждой производящей функции равна нулю.
Это свойство вообще уникально. Оно порождает
математические "кварки", ибо нормирование функции приводит к появлению дробных
значений коэффициентов. Рассмотрим, для примера, следующую производящую функцию
(1-х)2=1-2х+х2.
В этой функции три члена (триединство). Если
в этой функции пронормировать коэффициенты, то мы получим
3((1/3) -
(2/3)х +(1/3)х2)
Не напоминает ли
набор коэффициентов (1/3 -2/3 +1/3)
свойства кварков - виртуальных частиц физики
микромира, из которых сложены большинство семейств
элементарных частиц? Таким образом,
используя данную производящую функцию, мы можем построить производящие функции
для всех семейств "элементарных частиц",
таким образом, чтобы сумма коэффициентов получалась равной 1.
Так, полагая
s=1/3, d=1/3, u= -2/3 и
дополняя бином (1-х)2=1-2х+1,
биномом -(1-х)2, и отождествяя первый
бином с антитриадой кварков, а второй - с триадой, мы получаем механизм для
порождения "мезонных" частиц (Законы микромира).
рис. 8
На
страницах сайта мы показали связь этих функций с формированием подоболочек
и оболочек Периодической системы химических элементов.
Отметим некоторые важнейшие свойства этих
функций.
Биномиальные коэффициенты характеризуются
замечательными свойствами.
1.
Характеризуются замечательно
простым алгоритмом их получения. Каждый коэффициент в нижележащем многочлене
является суммой коэффициентов, расположенных над ним, например, 3+3=6, 1+3=4, и
т.д.
2. В
этом треугольнике в каждой производящей функции первый и последний
коэффициент равен единице.
3. Сумма коэффициентов в каждой производящей функции равна нулю.
Это свойство вообще уникально. Оно порождает
математические "кварки", ибо нормирование функции приводит к появлению дробных
значений коэффициентов. Рассмотрим, для примера, следующую производящую функцию
(1-х)2=1-2х+х2.
В этой функции три члена (триединство). Если
в этой функции пронормировать коэффициенты, то мы получим
3((1/3) -
(2/3)х +(1/3)х2)
Не напоминает ли
набор коэффициентов (1/3 -2/3 +1/3)
свойства кварков - виртуальных частиц физики
микромира, из которых сложены большинство семейств
элементарных частиц? Таким образом,
используя данную производящую функцию, мы можем построить производящие функции
для всех семейств "элементарных частиц",
таким образом, чтобы сумма коэффициентов получалась равной 1.
Так, полагая
s=1/3, d=1/3, u= -2/3 и
дополняя бином (1-х)2=1-2х+1,
биномом -(1-х)2, и отождествяя первый
бином с антитриадой кварков, а второй - с триадой, мы получаем механизм для
порождения "мезонных" частиц (Законы микромира).
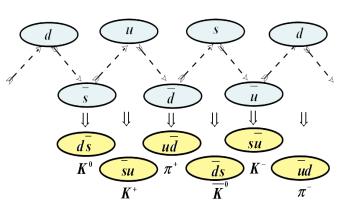 рис.9
Например, производящая функция для
ds
будет являться бином
(двойственное отношение)
-(1/3)х2+ (1/3)= (1/3)(-х2+1).
Здесь в правой части стоит квадратическая форма
вида
Zn+1
->
Z 2n
+ С
Стрелка
(->) означает итерацию.
Используя эту форму Мандельброт
совершил кардинальный прорыв в науке, ибо эта форма и породила удивительно
фантастический мир фракталов.
Слева в производящей функции стоит
нормировочный множитель, отражающий относительный "вес" членов бинома.
4.
Производящая функция обладает генной памятью.
Она позволяет, зная коэффициенты производящей функции, восстановить исходную
структуру, т.е. процесс восстановления исходного двучлена (монады) в нашем
случае однозначен. Процесс возрождения закончится, когда число членов
производящей функции будет равно двум (монада с внешней двойственностью), или
одному (монада с внутренней двойственностью).
Таким образом, вышеприведенная информация свидетельствует о тесной связи
фракталов с этими производящими функциями.
4. ОПЕРАТОРЫ ИНВАРИАНТНЫХ ПРЕОБРАЗОВАНИЙ
ПРОИЗВОДЯЩИХ ФУНКЦИЙ
Из анализа приведенных
выше свойств производящих функций,
используя две группы операторов
рис.9
Например, производящая функция для
ds
будет являться бином
(двойственное отношение)
-(1/3)х2+ (1/3)= (1/3)(-х2+1).
Здесь в правой части стоит квадратическая форма
вида
Zn+1
->
Z 2n
+ С
Стрелка
(->) означает итерацию.
Используя эту форму Мандельброт
совершил кардинальный прорыв в науке, ибо эта форма и породила удивительно
фантастический мир фракталов.
Слева в производящей функции стоит
нормировочный множитель, отражающий относительный "вес" членов бинома.
4.
Производящая функция обладает генной памятью.
Она позволяет, зная коэффициенты производящей функции, восстановить исходную
структуру, т.е. процесс восстановления исходного двучлена (монады) в нашем
случае однозначен. Процесс возрождения закончится, когда число членов
производящей функции будет равно двум (монада с внешней двойственностью), или
одному (монада с внутренней двойственностью).
Таким образом, вышеприведенная информация свидетельствует о тесной связи
фракталов с этими производящими функциями.
4. ОПЕРАТОРЫ ИНВАРИАНТНЫХ ПРЕОБРАЗОВАНИЙ
ПРОИЗВОДЯЩИХ ФУНКЦИЙ
Из анализа приведенных
выше свойств производящих функций,
используя две группы операторов
 видно,
что инвариантные преобразования производящих функций (рис. 8) порождают
удивительно гармоничные структуры
видно,
что инвариантные преобразования производящих функций (рис. 8) порождают
удивительно гармоничные структуры
 рис. 10
На этом рисунке показаны инвариантные преобразования производящих функций при
"обходе по кресту".
Из рисунка 10 видно. что производящие функции формируют двойную спираль.
Одна спираль восходящая, друга нисходящая.
рис. 10
На этом рисунке показаны инвариантные преобразования производящих функций при
"обходе по кресту".
Из рисунка 10 видно. что производящие функции формируют двойную спираль.
Одна спираль восходящая, друга нисходящая.
 Да и
не удивительно, ибо используемые операторы образуют "крест"
Да и
не удивительно, ибо используемые операторы образуют "крест"
 Заметим, и это чрезвычайно важно, что в
этом кресте ЗАПРЕЩЕНЫ
операторы
G0<->P1
и G1<->P0
,
что при формировании молекулы ДНК существуют аналогичные зависимости, и,
следовательно, можно придти к выводу, что молекула ДНК не является чудом
природы, а она, как и все другие "чудеса", формируется "по образу и подобию".
напомним,
что
существуют четыре
(!!) типа
азотистых оснований:
аденин
и гуанин
(азотистые основания пуринового ряда), тимин
и цитозин
(основания пиримидинового ряда). Их сокращенно обозначают по
начальным буквам: А, Г, Т, Ц.
Каждая горизонтальная «перекладина»
содержит либо аденин и тимин (А—Т
или Т—А), либо
гуанин и цитозин (Г—Ц
или Ц—Г).
Соединения аденина с гуанином (А-Г),
а также тимина с цитозином (Т-Ц)
не реализуются.
Сопоставляя
G0=Т,
P0 =A,
P1
=Ц, G1=Г,
мы
видим полное совпадение механизмов формирования производящих функций и
механизмов формирования молекул ДНК.
5. МАТЕМАТИЧЕСКИЕ КВАРКИ
О свойствах физических кварков можно получить дополнительную информацию на
странице "О кварках". По аналогии с физическими
кварками, которых никто не видел, и не наблюдал в эксперименте, но из которых
физики сложили мезонное и барионное семейства элементарных частиц, попытаемся
теперь сложить фрактальные семейства из математических кварков, свойства
которых можно не только наблюдать, но и описать математически. Можно даже
пойти далее и сказать, что физические кварки отражают структурный аспект
формирования семейств элементарных частиц, а математические кварки
отражают свойства функционального аспекта семейств элементарных частиц.
В определенной степени можно даже высказать идею об объединении свойств
кварков и говорить об их структурно-функциональном дуализме.
Выше мы уже приводили следующую
производящую функцию -трехчлен
(1-х)2=1х0-2х1+1х2.
Нормируя эту функцию мы получили следующее
выражение
3((1/3)х0 -
(2/3)х1 +(1/3)х2)
Однако нормирование, как обычно, означает "замыкание" системы в "единичную" и
пересчет "весов" ее "членов" относительно единицы. Следовательно, коэффициенты
этой производящей функции, замкнувшейся в единичную, будут пересчитаны.
Обозначая
части производящей функции символами
Заметим, и это чрезвычайно важно, что в
этом кресте ЗАПРЕЩЕНЫ
операторы
G0<->P1
и G1<->P0
,
что при формировании молекулы ДНК существуют аналогичные зависимости, и,
следовательно, можно придти к выводу, что молекула ДНК не является чудом
природы, а она, как и все другие "чудеса", формируется "по образу и подобию".
напомним,
что
существуют четыре
(!!) типа
азотистых оснований:
аденин
и гуанин
(азотистые основания пуринового ряда), тимин
и цитозин
(основания пиримидинового ряда). Их сокращенно обозначают по
начальным буквам: А, Г, Т, Ц.
Каждая горизонтальная «перекладина»
содержит либо аденин и тимин (А—Т
или Т—А), либо
гуанин и цитозин (Г—Ц
или Ц—Г).
Соединения аденина с гуанином (А-Г),
а также тимина с цитозином (Т-Ц)
не реализуются.
Сопоставляя
G0=Т,
P0 =A,
P1
=Ц, G1=Г,
мы
видим полное совпадение механизмов формирования производящих функций и
механизмов формирования молекул ДНК.
5. МАТЕМАТИЧЕСКИЕ КВАРКИ
О свойствах физических кварков можно получить дополнительную информацию на
странице "О кварках". По аналогии с физическими
кварками, которых никто не видел, и не наблюдал в эксперименте, но из которых
физики сложили мезонное и барионное семейства элементарных частиц, попытаемся
теперь сложить фрактальные семейства из математических кварков, свойства
которых можно не только наблюдать, но и описать математически. Можно даже
пойти далее и сказать, что физические кварки отражают структурный аспект
формирования семейств элементарных частиц, а математические кварки
отражают свойства функционального аспекта семейств элементарных частиц.
В определенной степени можно даже высказать идею об объединении свойств
кварков и говорить об их структурно-функциональном дуализме.
Выше мы уже приводили следующую
производящую функцию -трехчлен
(1-х)2=1х0-2х1+1х2.
Нормируя эту функцию мы получили следующее
выражение
3((1/3)х0 -
(2/3)х1 +(1/3)х2)
Однако нормирование, как обычно, означает "замыкание" системы в "единичную" и
пересчет "весов" ее "членов" относительно единицы. Следовательно, коэффициенты
этой производящей функции, замкнувшейся в единичную, будут пересчитаны.
Обозначая
части производящей функции символами
s=(-1/3)x0
u=(+2/3)x1
d=(-1/3)x2
s=(+1/3)x0
u=(-2/3)x1
d=(+1/3)x0
Мы получим два кварковых набора, из которых можно построить мезонное и
барионное фрактальные семейства.
Напомним, что существуют два
семейства элементарных частиц, построенных из физических кварков.

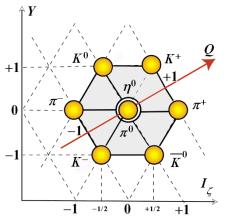 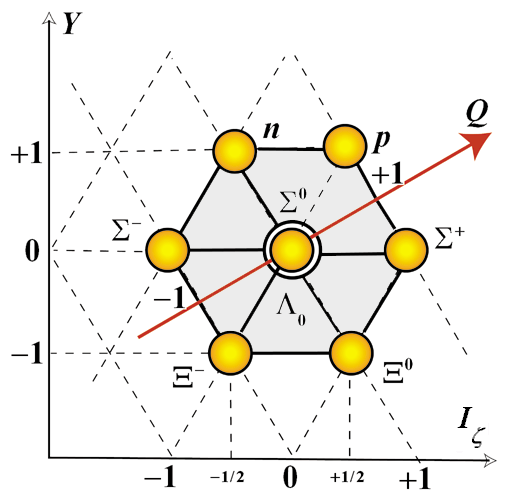 рис. 11
рис. 12
Эти семейства построены из набора кварков, сгруппированных следующим
образом.
рис. 11
рис. 12
Эти семейства построены из набора кварков, сгруппированных следующим
образом.
 рис. 13
рис. 14
Расписывая
частицы мезонного семейства (рис. 11), используя математические кварки,
мы получим
рис. 13
рис. 14
Расписывая
частицы мезонного семейства (рис. 11), используя математические кварки,
мы получим
ds=<(+1/3)x2,
(-1/3)x0,>
su=<(-1/3)x0,
(-2/3)x1,>
ud=<(-2/3)x1,(-1/3)x2,>
ds=<(-1/3)x2,(+1/3)x0,>
su=<(+1/3)x0,(+2/3)x1,>
ud=<((+2/3)x1,(+1/3)x2,>
Аналогично, расписывая частицы барионного семейства (рис. 12), используя
схему на рис. 14, мы получим
ssu=<(+1/3)x0,
+1/3)x0,(-2/3)x1,>
suu=<(+1/3)x0,
(-2/3)x1,(-2/3)x1>
uud=<(-2/3)x1,(-2/3)x1,(+1/3)x2,>
udd=<(-2/3)x1,(+1/3)x2,
(+1/3)x2,>
dds=<(+1/3)x2,(+1/3)x2,(+1/3)x0>
dss=<((+1/3)x2,(+1/3)x0,(+1/3)x0>
Таким образом, используя производящие функции, мы получили набор
функциональных кварков, порождающих мезонное и барионное производящие
фрактальные семейства.
Но мы получили только 6 частиц этих семейств, насчитывающих каждое по 9
частиц (рис.15).
 рис. 15
На рис. 13 и 14 эти три недостающие частицы размещены в центре гексады. Две
функциональные частицы будут представлять собой монаду с внешней
двойственностью, а третья -будет их Великим Пределом -монадой с внутренней
двойственностью.
Последняя и будет представлять собой целостную производящую функцию вида
3((1/3)х0 -
(2/3)х1 +(1/3)х2)
Но из каких частей этой функции будет состоять монада с внешней
двойственностью?
Заметим, что кварк s
представляет собой перенормируемый ВЕЛИКИЙ ПРЕДЕЛ, который имела монада в
Прошлом. Возможно поэтому физический кварк
s
обладает свойством, который
физики называют "странностью". Именно развертывание этого "прошлого" ВЕЛИКОГО
ПРЕДЕЛА и должно было породить монаду с внешней двойственностью, из которой
началось триумфальное "кварковое шествие", порождающее физические элементарные
частицы.
Перепишем вышеприведенный трехчлен в следующем виде
(+1/3)х0 +
(-2/3)х1 +(+1/3)х2)= (+1/3)х0 +х1(
(-2/3)х0 +(+1/3)х1)
В этом производящем многочлене мы видим два Великих Предела. Один существует в
Настоящем, а другой в скобках (в Прошлом). При этом Прошлое
представляется уже двучленом, а не трехчленом.
Если свойства исходной монады нашего "проявленного" мира могут
характеризоваться двучленом
(2/3)х1 +(1/3)х2=х1((2/3)х0+(1/3)х1),
то Великий Предел монады с внешней двойственностью будет
характеризоваться триединством.
Процессы сворачивания и разворачивания Великого Предела, отражающего свойства
инвариантности фазовых переходов из одного собственного пространства в
другое, подробно обосновано на странице "Концепции".
Таким образом, производящие функции, порождающие
семейства физических частиц, несут в себе генетическую память о Прошлом. И
всякий раз, когда производящие кварки формируют целостный двучлен (трехчлен),
то происходит трансформация функции структуру, т.е. происходит
материализация.
6. СОБСТВЕННОЕ ПРОСТРАНСТВО И ВРЕМЯ
6.1. О СВОЙСТВАХ МОНАДЫ "ПРОСТРАНТСВО-ВРЕМЯ"
Никого уже не удивляется,
когда говорят, что каждая система имеет собственное время. Поэтому будет
естественным считать. что каждое собственное пространство имеет и собственное
время. Тогда, обозначая пространство символом
L, а
время - символом Т, мы можем обозначить условие единства Пространства и
Времени символом
LT.
Полагая, по аналогии,
что и Пространство и Время могут иметь собственные производящие функции вида
рис. 15
На рис. 13 и 14 эти три недостающие частицы размещены в центре гексады. Две
функциональные частицы будут представлять собой монаду с внешней
двойственностью, а третья -будет их Великим Пределом -монадой с внутренней
двойственностью.
Последняя и будет представлять собой целостную производящую функцию вида
3((1/3)х0 -
(2/3)х1 +(1/3)х2)
Но из каких частей этой функции будет состоять монада с внешней
двойственностью?
Заметим, что кварк s
представляет собой перенормируемый ВЕЛИКИЙ ПРЕДЕЛ, который имела монада в
Прошлом. Возможно поэтому физический кварк
s
обладает свойством, который
физики называют "странностью". Именно развертывание этого "прошлого" ВЕЛИКОГО
ПРЕДЕЛА и должно было породить монаду с внешней двойственностью, из которой
началось триумфальное "кварковое шествие", порождающее физические элементарные
частицы.
Перепишем вышеприведенный трехчлен в следующем виде
(+1/3)х0 +
(-2/3)х1 +(+1/3)х2)= (+1/3)х0 +х1(
(-2/3)х0 +(+1/3)х1)
В этом производящем многочлене мы видим два Великих Предела. Один существует в
Настоящем, а другой в скобках (в Прошлом). При этом Прошлое
представляется уже двучленом, а не трехчленом.
Если свойства исходной монады нашего "проявленного" мира могут
характеризоваться двучленом
(2/3)х1 +(1/3)х2=х1((2/3)х0+(1/3)х1),
то Великий Предел монады с внешней двойственностью будет
характеризоваться триединством.
Процессы сворачивания и разворачивания Великого Предела, отражающего свойства
инвариантности фазовых переходов из одного собственного пространства в
другое, подробно обосновано на странице "Концепции".
Таким образом, производящие функции, порождающие
семейства физических частиц, несут в себе генетическую память о Прошлом. И
всякий раз, когда производящие кварки формируют целостный двучлен (трехчлен),
то происходит трансформация функции структуру, т.е. происходит
материализация.
6. СОБСТВЕННОЕ ПРОСТРАНСТВО И ВРЕМЯ
6.1. О СВОЙСТВАХ МОНАДЫ "ПРОСТРАНТСВО-ВРЕМЯ"
Никого уже не удивляется,
когда говорят, что каждая система имеет собственное время. Поэтому будет
естественным считать. что каждое собственное пространство имеет и собственное
время. Тогда, обозначая пространство символом
L, а
время - символом Т, мы можем обозначить условие единства Пространства и
Времени символом
LT.
Полагая, по аналогии,
что и Пространство и Время могут иметь собственные производящие функции вида
 Здесь мы ограничились только 4-мя членами, формирующими начальный "крест"
производящей функции.
Распишем эволюцию трансформации Пространства (L)
и Времени (Т)
в виде производящей функции и отразим эволюцию этой функции в свастичной форме
(рис. 16).
Здесь мы ограничились только 4-мя членами, формирующими начальный "крест"
производящей функции.
Распишем эволюцию трансформации Пространства (L)
и Времени (Т)
в виде производящей функции и отразим эволюцию этой функции в свастичной форме
(рис. 16).
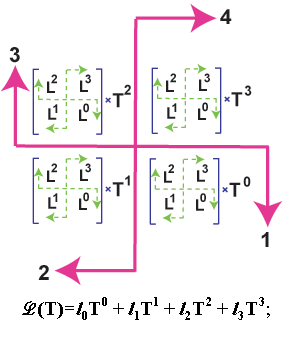
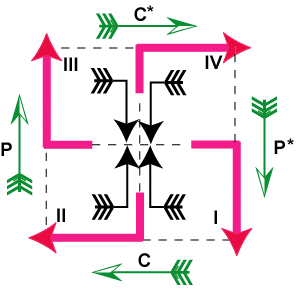 рис. 16
рис. 17
На данном рисунке эволюция
Пространства во Времени
отображена в форме вложенных друг в друга свастик (или крестов). По аналогии
можно построить производящий многочлен, отражающий эволюцию
Времени в Пространстве. На
странице "О свастике" достаточно подробно
обоснованы свойства законов отражения (С-, Р-, СР-, СРТ-инвариантности). Поэтому
здесь, связав с этими инвариантными преобразованиями последовательное
умножение матрицы
L
на
Т,
мы получили
представление о времени, как производящей функции многомерных пространств.
Нетрудно увидеть, что Время разделяет Пространства, отделяет их
друг от друга и придает им статус собственных, нормированных пространств.
Из производящей
функции Времени (рис. 16) можно построить Цветок Пространства-Времени.
Для этого каждой производящей функции
(рис. 1) сопоставим двойственную ей функцию вида
рис. 16
рис. 17
На данном рисунке эволюция
Пространства во Времени
отображена в форме вложенных друг в друга свастик (или крестов). По аналогии
можно построить производящий многочлен, отражающий эволюцию
Времени в Пространстве. На
странице "О свастике" достаточно подробно
обоснованы свойства законов отражения (С-, Р-, СР-, СРТ-инвариантности). Поэтому
здесь, связав с этими инвариантными преобразованиями последовательное
умножение матрицы
L
на
Т,
мы получили
представление о времени, как производящей функции многомерных пространств.
Нетрудно увидеть, что Время разделяет Пространства, отделяет их
друг от друга и придает им статус собственных, нормированных пространств.
Из производящей
функции Времени (рис. 16) можно построить Цветок Пространства-Времени.
Для этого каждой производящей функции
(рис. 1) сопоставим двойственную ей функцию вида
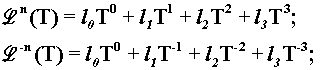 Статус времени как "равный среди равных" имеет под собой
более глубокое обоснование.
Из рассмотрения приведенных выше
производящих функций Времени и высказанной
гипотезе о равенстве временных и пространственных измерений следует, что могут
существовать инвариантные преобразования вида
L(T)<->T(L), отражающие
структурно-функциональный дуализм взаимоотношений Пространства и Времени (О
дуализме).
Не являются ли подобные
выражения отражением
структурно-функционального дуализма?
В этом случае можно сказать, что всякий раз, когда структура
сворачивается в ВЕЛИКИЙ ПРЕДЕЛ, то рождается производящая функция Времени, а
всякий раз, когда ВЕЛИКИЙ ПРЕДЕЛ разворачивается из нуль-пространства,
происходит трансформация
функции (времени) в
структуру (в пространство). Другими словами, время отражает в себе
функциональные свойства любого собственного пространства (Теория
иерархии), а ВЕЛИКИЙ ПРЕДЕЛ (Универсальный
закон) является точкой бифуркации, в которой могут осуществляться
инвариантные преобразования ПРОСТРАНСТВА и ВРЕМЕНИ. При этом ВЕЛИКИЙ ПРЕДЕЛ
(ЕДИНИЦА), характеризует целостность собственного ПРОСТРАНСТВА-ВРЕМЕНИ и
потому Великий Предел можно одновременно считать и нуль-пространством,
и нуль-временем.
Математически это можно записать следующим
образом
L(T)+T(L)=1
или, записывая последнее выражение в форме
L(T)=1
-T(L)
или
T(L)=1-L(T)
мы получим триединые представление о
ПРОСТРАНСТВЕ и_ВРЕМЕНИ.
Записывая полученные биномы в матричной форме, мы получим следующую матрицу,
отражающую эволюционные процессы трансформации ПРОСТРАНСТВА-ВРЕМЕНИ.
Статус времени как "равный среди равных" имеет под собой
более глубокое обоснование.
Из рассмотрения приведенных выше
производящих функций Времени и высказанной
гипотезе о равенстве временных и пространственных измерений следует, что могут
существовать инвариантные преобразования вида
L(T)<->T(L), отражающие
структурно-функциональный дуализм взаимоотношений Пространства и Времени (О
дуализме).
Не являются ли подобные
выражения отражением
структурно-функционального дуализма?
В этом случае можно сказать, что всякий раз, когда структура
сворачивается в ВЕЛИКИЙ ПРЕДЕЛ, то рождается производящая функция Времени, а
всякий раз, когда ВЕЛИКИЙ ПРЕДЕЛ разворачивается из нуль-пространства,
происходит трансформация
функции (времени) в
структуру (в пространство). Другими словами, время отражает в себе
функциональные свойства любого собственного пространства (Теория
иерархии), а ВЕЛИКИЙ ПРЕДЕЛ (Универсальный
закон) является точкой бифуркации, в которой могут осуществляться
инвариантные преобразования ПРОСТРАНСТВА и ВРЕМЕНИ. При этом ВЕЛИКИЙ ПРЕДЕЛ
(ЕДИНИЦА), характеризует целостность собственного ПРОСТРАНСТВА-ВРЕМЕНИ и
потому Великий Предел можно одновременно считать и нуль-пространством,
и нуль-временем.
Математически это можно записать следующим
образом
L(T)+T(L)=1
или, записывая последнее выражение в форме
L(T)=1
-T(L)
или
T(L)=1-L(T)
мы получим триединые представление о
ПРОСТРАНСТВЕ и_ВРЕМЕНИ.
Записывая полученные биномы в матричной форме, мы получим следующую матрицу,
отражающую эволюционные процессы трансформации ПРОСТРАНСТВА-ВРЕМЕНИ.
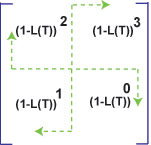 Свастика бинома (
L(T)=1
-T(L)
или
T(L)=1-L(T)
) порождает производящую функцию
ПРОСТРАНСТВА_-ВРЕМЕНИ (Преемственность), т.е. мы
снова получаем производящую функцию бинома Ньютона
Ln(T)=(1
-T(L))n
или
Tn(L)=(1-L(T))n
Эти производящие функции порождают структуры и функции Периодической системы
химических элементов (О химических элементах).
На странице "Преемственность"
было отмечено, что функции
Свастика бинома (
L(T)=1
-T(L)
или
T(L)=1-L(T)
) порождает производящую функцию
ПРОСТРАНСТВА_-ВРЕМЕНИ (Преемственность), т.е. мы
снова получаем производящую функцию бинома Ньютона
Ln(T)=(1
-T(L))n
или
Tn(L)=(1-L(T))n
Эти производящие функции порождают структуры и функции Периодической системы
химических элементов (О химических элементах).
На странице "Преемственность"
было отмечено, что функции
P(x)=(1-x)-x и G(x)=(1-x)P(x)
и
P*(x)=(1-x)+x
и G*(x)=(1-x)P*(x)
по своим свойствам являются по отношению друг к
другу являются обратными (противоположными), т.е. для них
будут справедливы отношения
P(x)/P*(x)=G(x)/G*(x)=1
Следовательно, эти отношения формируют
ВЕЛИКИЙ ПРЕДЕЛ.
Инвариантные преобразования ВЕЛИКОГО ПРЕДЕЛА
ПРОСТРАНСТВА -ВРЕМЕНИ можно продемонстрировать на следующем рисунке.
 рис. 18
В
центре этого рисунка располагается ВЕЛИКИЙ ПРЕДЕЛ ПРОСТРАНСТВА-ВРЕМЕНИ.
В этом ВЕЛИКОМ ПРЕДЕЛЕ Пространство
и Время свернуто в нуль-координату, т.е. в этой точке нет ни пространства, ни
времени. Отметим,
что 4-х мерном физическом
пространстве-времени, в котором время рассматривается как 4-е измерение, длина
"пространство" уменьшается по мере приближения скорости движущегося тела
к скорости света, а время жизни частиц, движущихся со скоростью света, будет
не ограничено (нет ограничения на время).
Таким образом, ВЕЛИКИЙ ПРЕДЕЛ ПРОСТРАНСТВА и ВРЕМЕНИ отражает равноправные
отношения между Пространством и Временем. Этот поистине ВЕЛИКИЙ ПРЕДЕЛ
отражает единство единство структурно-функционального дуализма ПРОСТРАНСТВА
-ВРЕМЕНИ, а ЦВЕТОК ЖИЗНИ ПРОСТРАНСТВА-ВРЕМЕНИ отражает синхронность и
синфазность процессов взаимотрансформации ПРОСТРАНСТВА и ВРЕМЕНИ.
Структурно-функциональный дуализм систем позволяет более глубоко понять физику
взаимосвязи Пространства и Времени.
Поскольку
физика изучает природу посредством анализа ПРОСТРАНСТВА СОБЫТИЙ, то,
исследуя это пространство, физик невольно сталкивается с двойственным подходом
к разрешению этой проблемы.
рис. 18
В
центре этого рисунка располагается ВЕЛИКИЙ ПРЕДЕЛ ПРОСТРАНСТВА-ВРЕМЕНИ.
В этом ВЕЛИКОМ ПРЕДЕЛЕ Пространство
и Время свернуто в нуль-координату, т.е. в этой точке нет ни пространства, ни
времени. Отметим,
что 4-х мерном физическом
пространстве-времени, в котором время рассматривается как 4-е измерение, длина
"пространство" уменьшается по мере приближения скорости движущегося тела
к скорости света, а время жизни частиц, движущихся со скоростью света, будет
не ограничено (нет ограничения на время).
Таким образом, ВЕЛИКИЙ ПРЕДЕЛ ПРОСТРАНСТВА и ВРЕМЕНИ отражает равноправные
отношения между Пространством и Временем. Этот поистине ВЕЛИКИЙ ПРЕДЕЛ
отражает единство единство структурно-функционального дуализма ПРОСТРАНСТВА
-ВРЕМЕНИ, а ЦВЕТОК ЖИЗНИ ПРОСТРАНСТВА-ВРЕМЕНИ отражает синхронность и
синфазность процессов взаимотрансформации ПРОСТРАНСТВА и ВРЕМЕНИ.
Структурно-функциональный дуализм систем позволяет более глубоко понять физику
взаимосвязи Пространства и Времени.
Поскольку
физика изучает природу посредством анализа ПРОСТРАНСТВА СОБЫТИЙ, то,
исследуя это пространство, физик невольно сталкивается с двойственным подходом
к разрешению этой проблемы.
 1. При анализе пространства СОБЫТИЙ
физик может выводить уравнения, характеризующие ПРОЦЕСС ПЕРЕМЕН
(функциональный аспект). Выявив функции, можно затем отразить и СОБЫТИЯ,
отражающие ПЕРЕМЕНЫ. 1. При анализе пространства СОБЫТИЙ
физик может выводить уравнения, характеризующие ПРОЦЕСС ПЕРЕМЕН
(функциональный аспект). Выявив функции, можно затем отразить и СОБЫТИЯ,
отражающие ПЕРЕМЕНЫ.
 2. Провести анализ
ПРОСТРАНСТВА СОБЫТИЙ и на его основе определить геометрические свойства
ПРОСТРАНСТВА СОБЫТИЙ, отражающих ПЕРЕМЕНЫ (структурный аспект). А зная
геометрию пространства, можно затем выявить и уравнения движения СОБЫТИЙ в
процессе их ПЕРЕМЕН.
6.2.
ОПЕРАТОРЫ СОБСТВЕННОГО ПРОСТРАНСТВА-ВРЕМЕНИ
Дуализм пространства и времени наиболее рельефно проявляется в свойствах
гексаграмм Книги Перемен (Книга
перемен). Это единство триграммы ЯН и ИНЬ, сливающихся в
ВЕЛИКИЙ ПРЕДЕЛ -гексаграмму.
Следовательно, мы можем говорить о том, что каждая гексаграмма матрицы И-Цзин
представляет собой монаду, которая может порождать собственный Цветок Жизни.
Тогда, обозначая гексаграмму Ян символом L, а
гексаграмму Инь соответственно символом Т, мы
получим возможность введения базисных операторов частного дифференцирования
монады двойственного отношения.
1. Операторы по L - (¶/¶L),
по Т- (¶/¶Т)
и ¶2/(¶L¶Т).
2. Обратные операторы:
по L -
1/(¶/¶L),
по Т-1/
(¶/¶Т)
и 1/¶2/(¶L¶Т).
Эти базисные операторы образуют генотип двойной спирали эволюции монады "L-T".
2. Провести анализ
ПРОСТРАНСТВА СОБЫТИЙ и на его основе определить геометрические свойства
ПРОСТРАНСТВА СОБЫТИЙ, отражающих ПЕРЕМЕНЫ (структурный аспект). А зная
геометрию пространства, можно затем выявить и уравнения движения СОБЫТИЙ в
процессе их ПЕРЕМЕН.
6.2.
ОПЕРАТОРЫ СОБСТВЕННОГО ПРОСТРАНСТВА-ВРЕМЕНИ
Дуализм пространства и времени наиболее рельефно проявляется в свойствах
гексаграмм Книги Перемен (Книга
перемен). Это единство триграммы ЯН и ИНЬ, сливающихся в
ВЕЛИКИЙ ПРЕДЕЛ -гексаграмму.
Следовательно, мы можем говорить о том, что каждая гексаграмма матрицы И-Цзин
представляет собой монаду, которая может порождать собственный Цветок Жизни.
Тогда, обозначая гексаграмму Ян символом L, а
гексаграмму Инь соответственно символом Т, мы
получим возможность введения базисных операторов частного дифференцирования
монады двойственного отношения.
1. Операторы по L - (¶/¶L),
по Т- (¶/¶Т)
и ¶2/(¶L¶Т).
2. Обратные операторы:
по L -
1/(¶/¶L),
по Т-1/
(¶/¶Т)
и 1/¶2/(¶L¶Т).
Эти базисные операторы образуют генотип двойной спирали эволюции монады "L-T".
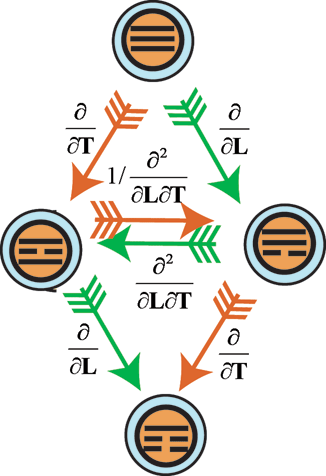
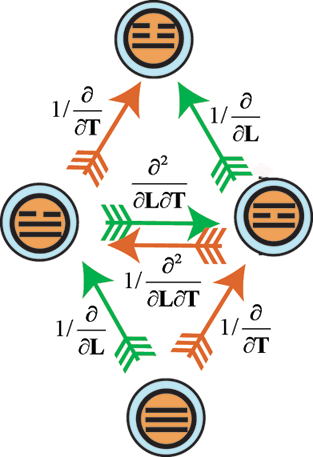 рис. 19 а рис.
19 б
В этих рисунках каждый крест является двойным, который может быть представлен
в форме двойной спирали (рис. 20).
рис. 19 а рис.
19 б
В этих рисунках каждый крест является двойным, который может быть представлен
в форме двойной спирали (рис. 20).
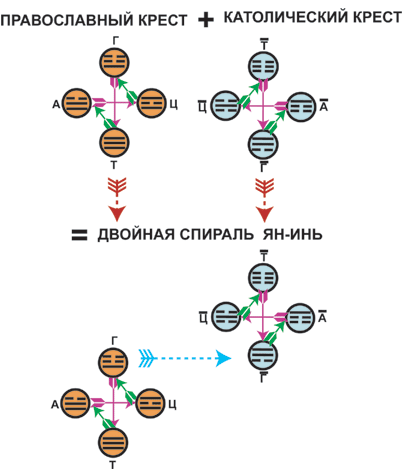 рис. 20
Нетрудно увидеть, что каждая стрелка в этой двойной спирали отражает тот или
иной оператор из базисного набора операторов двойственного отношения.
рис. 20
Нетрудно увидеть, что каждая стрелка в этой двойной спирали отражает тот или
иной оператор из базисного набора операторов двойственного отношения.
 рис. 21
Таким образом, мы получили ГЕНОТИП эволюции двойственного отношения ЯН-ИНЬ. Из
которого нетрудно построить и ГЕНОМ.
На страницах сайта (О
механизмах хозяйствования, и др.), рассматривая свойства
эволюции двойственного отношения, неоднократно рассматривалось свойства
операций умножения и деления на кресте
(умножить,
умножить, разделить) .
1.
1
2.
1*(¶/¶L)
3.
1*(¶/¶L)*(¶/¶T)
4. 1*((¶/¶L)*(¶/¶T)*1/¶2/(¶L¶Т)=1
5.
1/((¶/¶L)
6. (1/((¶/¶L))*(1/(¶/¶T)
7.
(1/((¶/¶L))*(1/(¶/¶T)
*¶2/(¶L¶Т)=1
8.
1
На многих страницах сайта показывается, как свойства операторов монады ЯН-ИНЬ
(рис. 19-21) порождают животворящие кресты, свастики, тетраэдры, звездные
тетраэдры, кубы, державы, Древо Жизни и ДРЕВНИЙ ЦВЕТОК ЖИЗНИ, который,
действительно, в явном виде отражает
все самые сокровенные тайны МИРОЗДАНИЯ и содержит в себе ВСЕ ФОРМУЛЫ, ДО
ОДНОЙ.
рис. 21
Таким образом, мы получили ГЕНОТИП эволюции двойственного отношения ЯН-ИНЬ. Из
которого нетрудно построить и ГЕНОМ.
На страницах сайта (О
механизмах хозяйствования, и др.), рассматривая свойства
эволюции двойственного отношения, неоднократно рассматривалось свойства
операций умножения и деления на кресте
(умножить,
умножить, разделить) .
1.
1
2.
1*(¶/¶L)
3.
1*(¶/¶L)*(¶/¶T)
4. 1*((¶/¶L)*(¶/¶T)*1/¶2/(¶L¶Т)=1
5.
1/((¶/¶L)
6. (1/((¶/¶L))*(1/(¶/¶T)
7.
(1/((¶/¶L))*(1/(¶/¶T)
*¶2/(¶L¶Т)=1
8.
1
На многих страницах сайта показывается, как свойства операторов монады ЯН-ИНЬ
(рис. 19-21) порождают животворящие кресты, свастики, тетраэдры, звездные
тетраэдры, кубы, державы, Древо Жизни и ДРЕВНИЙ ЦВЕТОК ЖИЗНИ, который,
действительно, в явном виде отражает
все самые сокровенные тайны МИРОЗДАНИЯ и содержит в себе ВСЕ ФОРМУЛЫ, ДО
ОДНОЙ.
 рис. 22
Посмотрите и увидьте, что каждый лепесток этого Цветка ЖИЗНИ порождается тем,
или иным базисным оператором дифференцирования (или обратным оператором) и
каждый лепесток, каждого лепестка этого ЦВЕТКА может порождать собственный
ЦВЕТОК ЖИЗНИ. Так рождаются ГЕНОТИПЫ (Геном Вселенной)
монад "ЯН-ИНЬ". Так рождаются ГЕНОТИПЫ собственного
пространства-времени.
Так рождается фрактальная реальность. ТАК
РОЖДАЮТСЯ ВСЕ ФОРМУЛЫ МИРОЗДАНИЯ.
Если кому-то
покажется, что все это бред, то просьба далее не беспокоиться. ЭТО УЖЕ НЕ ДЛЯ
ВАС и ЭТО УЖЕ НАВСЕГДА, ИБО ОБЪЕКТИВНАЯ РЕАЛЬНОСТЬ ДЛЯ ВАС ЯВЛЯЕТСЯ
НЕДОСТАТОЧНО УБЕДИТЕЛЬНОЙ.
Все остальные могут вспомнить свойства экспоненциальных функций (Иерархия
функций,
Геном памяти), если параметр "х"
в этих функциях заменить монадой "L*T",
а также получить дополнительную информацию на странице "Эволюция
размерности", где на основе такого "бреда" обосновывается
ПЕРИОДИЧЕСКИЙ ЗАКОН эволюции физических величин (мировых
констант), имеющих статус "равных среди равных".
7. О СОБСТВЕННОМ ПРОСТРАНСТВЕ ВАКУУМА
Собственное
пространство вакуума можно отождествить с "пустым" пространством, в котором
нет собственных векторов и собственных значений (собственные вектора,
свернутые в точку).
Но любое собственное пространство при этом будет иметь геометрические свойства
и характеризоваться собственным ПРОСТРАНСТВОМ -ВРЕМЕНЕМ.
Из этих свойств "пустого" собственного пространства следует, что собственное
пространство всегда будет характеризоваться или структурным, или
функциональным аспектом, или отражать ВЕЛИКИЙ ПРЕДЕЛ этих аспектов.
О геометрических свойствах собственных пространств можно судить по системам
отсчета, которые используются в физике. В физике
существует несколько классов инерциальных систем отсчета.
1. Инерциальные системы отсчета, движение в которых происходит
равномерно.
2. Инерциальные системы отсчета, движение в которых осуществляется с
ускорением.
3. Конморфные инерциальные системы отсчета.
Отметим, что в последнем классе систем отсчета системы связаны с
физическими объектами, которые в течением времени могут изменять свои
физические характеристики.
С точки зрения собственных пространств это означает, что такие физические
объекты характеризуют дополнительные измерения. Если такой физический
объект не будет изменяться с течением времени, то такой объект в рамках
собственного пространства будет характеризовать собственный вектор, или
собственное значение, соответствующего собственного пространства,
подпространства.
Рассмотрим теперь некоторые свойства
физического вакуума, с которым работают физики.
7.1. СОБСТВЕННОЕ ПРОСТРАНСТВО-ВРЕМЯ по
ЭЙНШТЕЙНУ
Собственное пространство в специальной теории
относительности Эйнштейна включает в себя 3-х мерное пространство и в качестве
собственного вектора дополнительного измерения (4-е измерение) включает в себя
время. Это собственное пространство-время и отражает в себе свойства вакуума
по Эйнштейну. В них не включается, и не описываются свойства материи. Они не
содержат никаких физических констант и переменных. если бы такие уравнения
содержали бы подобные дополнительные измерения, то они бы описывали какое-либо
собственное, но уже материализованное пространство.
Это свойство
собственных пространств и легло в основу многих описаний свойств
физического вакуума. Здесь все изумительно просто. Достаточно в такое
собственное пространство включить свойства материи и мы будем получать
материальные объекты непосредственно из "пустого" вакуума.
7.2. ВАКУУМ ДИРАКА
В основе положений
Дирака о вакууме лежат открытые им уравнения, которые показывают,
что в природе частицы с отрицательно энергией (электроны) и частицы с
положительной энергией (позитроны) рождаются парами. Поистине замечательное
открытие!
Самое общее представление о вакууме Дирака сводится к тому, что в малых
пространственных областях вакуума (порядка 10-33), значения
физических характеристик вакуума могут стать отличными от нуля, т.е.
на малых расстояниях вакуум "дышит", "кипит", порождая и поглощая элементарные
частицы. Физики называют такие процессы спонтанными флуктуациями.
А может быть, уравнения Дирака отражают свойства ВЕЛИКОГО ПРЕДЕЛА?
Если теперь электрон отождествить с символом
T(L),
а позитрон - соответственно с символом
L(T),
то у нас
возникнут, по аналогии, ассоциация о тождественности
преобразований
L(T)=1
-T(L)
или
T(L)=1-L(T)
осуществляемый через ВЕЛИКИЙ ПРЕДЕЛ подобных пар.
Может быть, уравнения Дирака и отражают сущность подобных
преобразований. Но тогда станет понятной, что за "горизонтом осознания"
ВЕЛИКОГО ПРЕДЕЛА лежит уже не пустота, а иное собственное
ПРОСТРАНСТВО-ВРЕМЯ.
7.3. ВАКУУМ
по ШИПОВУ
Основные уровни реальности в теории физического вакуума, созданной Г.И.
Шиповым, на самом верхнем уровне включают в себя "АБСОЛЮТНОЕ "НИЧТО". Но
ни одна теория относительности, включающая в себя хотя бы одну абсолютную
константу уже по определению не может претендовать на всеобщность. Для этого
Абсолютного "НИЧТО" Геннадий Иванович водит следующее тождество
рис. 22
Посмотрите и увидьте, что каждый лепесток этого Цветка ЖИЗНИ порождается тем,
или иным базисным оператором дифференцирования (или обратным оператором) и
каждый лепесток, каждого лепестка этого ЦВЕТКА может порождать собственный
ЦВЕТОК ЖИЗНИ. Так рождаются ГЕНОТИПЫ (Геном Вселенной)
монад "ЯН-ИНЬ". Так рождаются ГЕНОТИПЫ собственного
пространства-времени.
Так рождается фрактальная реальность. ТАК
РОЖДАЮТСЯ ВСЕ ФОРМУЛЫ МИРОЗДАНИЯ.
Если кому-то
покажется, что все это бред, то просьба далее не беспокоиться. ЭТО УЖЕ НЕ ДЛЯ
ВАС и ЭТО УЖЕ НАВСЕГДА, ИБО ОБЪЕКТИВНАЯ РЕАЛЬНОСТЬ ДЛЯ ВАС ЯВЛЯЕТСЯ
НЕДОСТАТОЧНО УБЕДИТЕЛЬНОЙ.
Все остальные могут вспомнить свойства экспоненциальных функций (Иерархия
функций,
Геном памяти), если параметр "х"
в этих функциях заменить монадой "L*T",
а также получить дополнительную информацию на странице "Эволюция
размерности", где на основе такого "бреда" обосновывается
ПЕРИОДИЧЕСКИЙ ЗАКОН эволюции физических величин (мировых
констант), имеющих статус "равных среди равных".
7. О СОБСТВЕННОМ ПРОСТРАНСТВЕ ВАКУУМА
Собственное
пространство вакуума можно отождествить с "пустым" пространством, в котором
нет собственных векторов и собственных значений (собственные вектора,
свернутые в точку).
Но любое собственное пространство при этом будет иметь геометрические свойства
и характеризоваться собственным ПРОСТРАНСТВОМ -ВРЕМЕНЕМ.
Из этих свойств "пустого" собственного пространства следует, что собственное
пространство всегда будет характеризоваться или структурным, или
функциональным аспектом, или отражать ВЕЛИКИЙ ПРЕДЕЛ этих аспектов.
О геометрических свойствах собственных пространств можно судить по системам
отсчета, которые используются в физике. В физике
существует несколько классов инерциальных систем отсчета.
1. Инерциальные системы отсчета, движение в которых происходит
равномерно.
2. Инерциальные системы отсчета, движение в которых осуществляется с
ускорением.
3. Конморфные инерциальные системы отсчета.
Отметим, что в последнем классе систем отсчета системы связаны с
физическими объектами, которые в течением времени могут изменять свои
физические характеристики.
С точки зрения собственных пространств это означает, что такие физические
объекты характеризуют дополнительные измерения. Если такой физический
объект не будет изменяться с течением времени, то такой объект в рамках
собственного пространства будет характеризовать собственный вектор, или
собственное значение, соответствующего собственного пространства,
подпространства.
Рассмотрим теперь некоторые свойства
физического вакуума, с которым работают физики.
7.1. СОБСТВЕННОЕ ПРОСТРАНСТВО-ВРЕМЯ по
ЭЙНШТЕЙНУ
Собственное пространство в специальной теории
относительности Эйнштейна включает в себя 3-х мерное пространство и в качестве
собственного вектора дополнительного измерения (4-е измерение) включает в себя
время. Это собственное пространство-время и отражает в себе свойства вакуума
по Эйнштейну. В них не включается, и не описываются свойства материи. Они не
содержат никаких физических констант и переменных. если бы такие уравнения
содержали бы подобные дополнительные измерения, то они бы описывали какое-либо
собственное, но уже материализованное пространство.
Это свойство
собственных пространств и легло в основу многих описаний свойств
физического вакуума. Здесь все изумительно просто. Достаточно в такое
собственное пространство включить свойства материи и мы будем получать
материальные объекты непосредственно из "пустого" вакуума.
7.2. ВАКУУМ ДИРАКА
В основе положений
Дирака о вакууме лежат открытые им уравнения, которые показывают,
что в природе частицы с отрицательно энергией (электроны) и частицы с
положительной энергией (позитроны) рождаются парами. Поистине замечательное
открытие!
Самое общее представление о вакууме Дирака сводится к тому, что в малых
пространственных областях вакуума (порядка 10-33), значения
физических характеристик вакуума могут стать отличными от нуля, т.е.
на малых расстояниях вакуум "дышит", "кипит", порождая и поглощая элементарные
частицы. Физики называют такие процессы спонтанными флуктуациями.
А может быть, уравнения Дирака отражают свойства ВЕЛИКОГО ПРЕДЕЛА?
Если теперь электрон отождествить с символом
T(L),
а позитрон - соответственно с символом
L(T),
то у нас
возникнут, по аналогии, ассоциация о тождественности
преобразований
L(T)=1
-T(L)
или
T(L)=1-L(T)
осуществляемый через ВЕЛИКИЙ ПРЕДЕЛ подобных пар.
Может быть, уравнения Дирака и отражают сущность подобных
преобразований. Но тогда станет понятной, что за "горизонтом осознания"
ВЕЛИКОГО ПРЕДЕЛА лежит уже не пустота, а иное собственное
ПРОСТРАНСТВО-ВРЕМЯ.
7.3. ВАКУУМ
по ШИПОВУ
Основные уровни реальности в теории физического вакуума, созданной Г.И.
Шиповым, на самом верхнем уровне включают в себя "АБСОЛЮТНОЕ "НИЧТО". Но
ни одна теория относительности, включающая в себя хотя бы одну абсолютную
константу уже по определению не может претендовать на всеобщность. Для этого
Абсолютного "НИЧТО" Геннадий Иванович водит следующее тождество
 .
Но как же быть с законами сохранения? Получается,
что на уровне микромира, там, где микромир граничит с иными "торсионными"
мирами, законы сохранения не работают?
Подобные постулаты нарушают целостность мироздания. СОБЫТИЕ -"НИЧТО" с точки
зрения юриспруденции является ничтожным. Поэтому процесс ПЕРЕМЕНЫ от
одного НИЧТО к другому НИЧТО просто не имеет смысла.
Поэтому к
законам сохранения надо
относиться, на мой взгляд, более бережно. Мне кажется, что здесь должно
выполняться тождество .
Но как же быть с законами сохранения? Получается,
что на уровне микромира, там, где микромир граничит с иными "торсионными"
мирами, законы сохранения не работают?
Подобные постулаты нарушают целостность мироздания. СОБЫТИЕ -"НИЧТО" с точки
зрения юриспруденции является ничтожным. Поэтому процесс ПЕРЕМЕНЫ от
одного НИЧТО к другому НИЧТО просто не имеет смысла.
Поэтому к
законам сохранения надо
относиться, на мой взгляд, более бережно. Мне кажется, что здесь должно
выполняться тождество  .
Это тождество, во-первых, отражает целостность мироздания, в котором нет числа
больше, чем 1 (Единица). На страницах сайта это свойство
собственных пространств рассматривается неоднократно. Такие единицы рождаются
всякий раз, когда "количество переходит в качество", когда "Последний
становится Первым". В этом случае происходит перенормировка всех собственных
значений и констант собственного пространства и все они, без исключения
становятся относительными, включая и время, которое имеет статус
параметра "равный среди равных". Другими словами ЕДИНИЦА -это всегда ВЕЛИКИЙ
ПРЕДЕЛ двойственного отношения. И это ВЕЛИКИЙ ПРЕДЕЛ может разворачиваться,
порождая соответствующие пары частиц, но не из пустоты. ВЕЛИКИЙ ПРЕДЕЛ
имеет генную память о своем прошлом (Генная память).
Поэтому там, за "горизонтом осознания" ВЕЛИКОГО ПРЕДЕЛА находится его ПРОШЛОЕ.
ЕДИНИЦА характеризует АБСОЛЮТ, ибо Единица, как самое большое число,
существует на всех уровнях мироздания, как его первокирпичик. Этот же
первокирпичик является и последним, отражая смысл тождества .
Это тождество, во-первых, отражает целостность мироздания, в котором нет числа
больше, чем 1 (Единица). На страницах сайта это свойство
собственных пространств рассматривается неоднократно. Такие единицы рождаются
всякий раз, когда "количество переходит в качество", когда "Последний
становится Первым". В этом случае происходит перенормировка всех собственных
значений и констант собственного пространства и все они, без исключения
становятся относительными, включая и время, которое имеет статус
параметра "равный среди равных". Другими словами ЕДИНИЦА -это всегда ВЕЛИКИЙ
ПРЕДЕЛ двойственного отношения. И это ВЕЛИКИЙ ПРЕДЕЛ может разворачиваться,
порождая соответствующие пары частиц, но не из пустоты. ВЕЛИКИЙ ПРЕДЕЛ
имеет генную память о своем прошлом (Генная память).
Поэтому там, за "горизонтом осознания" ВЕЛИКОГО ПРЕДЕЛА находится его ПРОШЛОЕ.
ЕДИНИЦА характеризует АБСОЛЮТ, ибо Единица, как самое большое число,
существует на всех уровнях мироздания, как его первокирпичик. Этот же
первокирпичик является и последним, отражая смысл тождества
 .
При этом каждый ВЕЛИКИЙ
ПРЕДЕЛ отражает СОБЫТИЕ, порождаемое процессом ПЕРЕМЕН и потому тождество
сущность ВЕЛИКОГО
ПРЕДЕЛА. Разворачивание ВЕЛИКОГО ПРЕДЕЛА приводят к ПЕРЕМЕНАМ, порождающих
цепочку СОБЫТИЙ, которые на первом этапе характеризуются процессами разложения
целого на части(анализ),
а затем синтеза-сборки целого из частей, в результате которой получается новая
Единица. И тождество приобретает более глубокий смысл. Оно отражает
цикличность эволюции ВЕЛИКОГО ПРЕДЕЛА и ОТНОСИТЕЛЬНОСТЬ АБСОЛЮТНОЙ
ЕДИНИЦЫ.
Теория Г.И. Шипова уже научилась извлекать ПРОШЛОЕ
ВЕЛИКОГО ПРЕДЕЛА из "НИЧТО". Но, все-таки, на мой взгляд извлечение
элементарных, и не только элементарных частиц, может оказаться более
эффективным, если эти частицы начнут извлекаться из АБСОЛЮТНОЙ ЕДИНИЦЫ.
И все же Истина оказывается более прекрасной. На страницах сайта мы уже
неоднократно обосновывали, что наши представления о монаде "Истина-Ложь",
являются только линейными, что отрицание Истины не порождает ложь, а всего
лишь означает иную Истину. Поэтому и двойное отрицание Истины отражает всего
лишь "откат" к предыдущей Истине, которая отрицалась последней. Поэтому
представляет смысл более внимательно присмотреться не к тождествам .
При этом каждый ВЕЛИКИЙ
ПРЕДЕЛ отражает СОБЫТИЕ, порождаемое процессом ПЕРЕМЕН и потому тождество
сущность ВЕЛИКОГО
ПРЕДЕЛА. Разворачивание ВЕЛИКОГО ПРЕДЕЛА приводят к ПЕРЕМЕНАМ, порождающих
цепочку СОБЫТИЙ, которые на первом этапе характеризуются процессами разложения
целого на части(анализ),
а затем синтеза-сборки целого из частей, в результате которой получается новая
Единица. И тождество приобретает более глубокий смысл. Оно отражает
цикличность эволюции ВЕЛИКОГО ПРЕДЕЛА и ОТНОСИТЕЛЬНОСТЬ АБСОЛЮТНОЙ
ЕДИНИЦЫ.
Теория Г.И. Шипова уже научилась извлекать ПРОШЛОЕ
ВЕЛИКОГО ПРЕДЕЛА из "НИЧТО". Но, все-таки, на мой взгляд извлечение
элементарных, и не только элементарных частиц, может оказаться более
эффективным, если эти частицы начнут извлекаться из АБСОЛЮТНОЙ ЕДИНИЦЫ.
И все же Истина оказывается более прекрасной. На страницах сайта мы уже
неоднократно обосновывали, что наши представления о монаде "Истина-Ложь",
являются только линейными, что отрицание Истины не порождает ложь, а всего
лишь означает иную Истину. Поэтому и двойное отрицание Истины отражает всего
лишь "откат" к предыдущей Истине, которая отрицалась последней. Поэтому
представляет смысл более внимательно присмотреться не к тождествам
 и и
 , а к тождеству , а к тождеству
 .
И это не мистика, а реалии Единого Закона. На страницах "Русская
матрица" и "Золотой
Путь"
мы приводили свойства
Русской матрицы и обосновали, что при использовании мультипликативных операций
над золотыми числами, центральным элементом этой матрицы является "1".
При использовании аддитивных операций над показателями степенных рядов,
составляющих строки, столбцы и диагонали этой матрицы у нас центральным
элементом является уже "0".
Вот мы и доказали, что Абсолютное НИЧТО (нуль) порождает ВСЕ (ЕДИНИЦУ).
Сегодня физика уже вплотную подошла к границе "осознанного мира" и теперь надо сделать
еще один шаг в иной, реальный мир, но существующий за "горизонтом осознания".
И этот мир уже нельзя называть Абсолютным "НИЧТО".
РЕЗЮМЕ
1. Собственные пространства
играют в новой науке очень важную роль. Они характеризуют природу квантования
всех явлений окружающей нас действительности, а симметрия преобразований
(инвариантность относительно этих преобразований) позволяет более глубоко понять
сущность Единого Универсального закона.
2. Собственные
пространства характеризуются свойством "структурно-функционального дуализма"
и порождаются производящими функциями двойственного отношения (монады).
3. Каждое собственное
пространство порождается собственными
производящими
функциями, играющими роль ВЕЛИКОГО ПРЕДЕЛА для этих собственных пространств.
Великий Предел, разворачиваясь порождает соответствующие семейства, обладающие
уже реальной структурой, т.е. разворачивание ВЕЛИКОГО ПРЕДЕЛА характеризует
процессы материализации его внутреннего содержимого, т.е. ВЕЛИКИЙ ПРЕДЕЛ несет
в себе генетическую память о своем собственном Прошлом.
4.
Справедливо и обратное утверждение - сворачивание монады с внешней
двойственностью в монаду с внутренней двойственностью, отражает процессы
дематериализации частиц. .
И это не мистика, а реалии Единого Закона. На страницах "Русская
матрица" и "Золотой
Путь"
мы приводили свойства
Русской матрицы и обосновали, что при использовании мультипликативных операций
над золотыми числами, центральным элементом этой матрицы является "1".
При использовании аддитивных операций над показателями степенных рядов,
составляющих строки, столбцы и диагонали этой матрицы у нас центральным
элементом является уже "0".
Вот мы и доказали, что Абсолютное НИЧТО (нуль) порождает ВСЕ (ЕДИНИЦУ).
Сегодня физика уже вплотную подошла к границе "осознанного мира" и теперь надо сделать
еще один шаг в иной, реальный мир, но существующий за "горизонтом осознания".
И этот мир уже нельзя называть Абсолютным "НИЧТО".
РЕЗЮМЕ
1. Собственные пространства
играют в новой науке очень важную роль. Они характеризуют природу квантования
всех явлений окружающей нас действительности, а симметрия преобразований
(инвариантность относительно этих преобразований) позволяет более глубоко понять
сущность Единого Универсального закона.
2. Собственные
пространства характеризуются свойством "структурно-функционального дуализма"
и порождаются производящими функциями двойственного отношения (монады).
3. Каждое собственное
пространство порождается собственными
производящими
функциями, играющими роль ВЕЛИКОГО ПРЕДЕЛА для этих собственных пространств.
Великий Предел, разворачиваясь порождает соответствующие семейства, обладающие
уже реальной структурой, т.е. разворачивание ВЕЛИКОГО ПРЕДЕЛА характеризует
процессы материализации его внутреннего содержимого, т.е. ВЕЛИКИЙ ПРЕДЕЛ несет
в себе генетическую память о своем собственном Прошлом.
4.
Справедливо и обратное утверждение - сворачивание монады с внешней
двойственностью в монаду с внутренней двойственностью, отражает процессы
дематериализации частиц.
e-mail:
С
благодарностью приму все ваши замечания, предложения,
с признательностью
отвечу на ваши вопросы
|






 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©