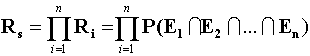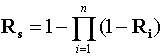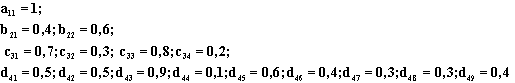СИСТЕМНЫЕ ТЕХНОЛОГИИ
УПРАВЛЕНИЯ КАЧЕСТВОМ
ВВЕДЕНИЕ
На данной странице
дается первое представление о системных технологиях и их свойствах, с точки
зрения Единого Закона.
Сегодня понятие "технология"
становится все более и более актуальным. Технология
из сферы производственной уже прочно интегрировалась со сферой научной.
Системные технологии стали предметом самостоятельных
теоретический исследований.
К людям постепенно приходит осознание,
что системные технологии, как теоретическая категория, не отражая в себе
физические свойства систем, где используются эти технологии, отражают
системные смыслы Событий и Перемен, происходящих в этих системах.
Милогия несет в себе
Единую Системную
Технологию, отражающую Единый План Творения
систем любой природы.
Законы
сохранения эволюционных потоков ЯН-ИНЬ отражают именно эти системные
качества Единого закона эволюции двойственного отношения (монады ЯН-ИНЬ).
На
страницах. указанных ниже приводятся некоторые свойства системных технологий
Единого закона, отражающих свойства эволюционных потоков ЯН-ИНЬ:
-
свойства эволюционных потоков ЯН-ИНЬ изложены
на страницах "Книга перемен",
"Потоки ЯН-Инь"и других,
-
свойства и типы монад, порождающих
соответствующие законы сохранения. приведены на странице "О
свастике",
-
свойства ресурсных потоков ЯН-ИНЬ и
законов их взаимотрансформаций отражены на странице "О
ресурсах".
Поэтому ниже приводим
только дополнительную информацию, позволяющую глубже осознать свойства
ресурсных потоков ЯН-ИНЬ. Эта информация отражает, в первую очередь,
аспекты взаимоотношений
количества и
качества.
Уже много
веков философы спорят о взаимоотношениях количества и качества. Уже философский
закон о перерастании количества в качество ни у кого не вызывает сомнения.
Этот закон гласит, что сумма "системных
смыслов" свойств элементов, не равна смыслу системы.
В теории систем
этот феномен качества проявляется как закон синергии (греч.- содействие,
сотрудничество): внешнее свойство результата
взаимодействия элементов организации, заключающееся в производстве
дополнительной энергии. превышающей сумму энергий участвующих в нем элементов.
Так, например, в физике микромира закон синергии проявляется в таком
феномене, как дефект массы.
1.КАЧЕСТВО
Рассмотрим применимость Единого закона к системных технологиям в ресурсных
системах экономических систем.
В самом общем случае качество определяется как
совокупность свойств и характеристик продукции или услуги, которые придают им
способность удовлетворять установленные или предполагаемые потребности, которые
могут включать в себя надежность, эксплуатационные характеристики,
функциональную пригодность, экономичность, эргономичность и т.п.
Отождествляя понятие
нужда с понятием
полезности, и полагая, что потребность\и связаны с
надежностью эксплуатационных характеристик и функциональной пригодности,
можно качество в самом общем случае представить как две пары
двойственных отношений (рис. 1).
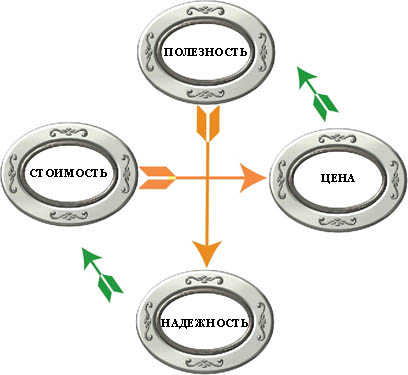
рис.
1
В данном кресте будет между плечами
перекладин будет выполняться пропорция
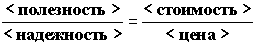
или
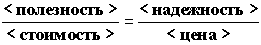 Если теперь, в соответствии с правилом обхода по
кресту мы можем записать, например, следующее выражение, характеризующее
взаимоотношения между компонентами качества системы
Если теперь, в соответствии с правилом обхода по
кресту мы можем записать, например, следующее выражение, характеризующее
взаимоотношения между компонентами качества системы
 Тогда общая схема системы
качества может быть представлена в виде схемы (рис. 2).
Тогда общая схема системы
качества может быть представлена в виде схемы (рис. 2).
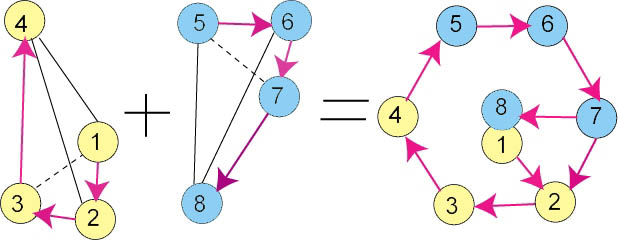 рис. 2
Если
тетраэдру с вершинами 1-4 сопоставить создание системы управления
качеством, то тетраэдр с вершинами 5-8 будет характеризовать сопровождение и
развитие системы управления качеством.
Если теперь в качестве альтернативных
двойственных перекладин креста выбрать двойственные пары
"нужда-потребность",
"запрос-товар",
то мы получим
крест потребителя,
характеризующий процесс возникновения потребительской нужды в определенном
товаре. Тогда крест производителя
будет характеризовать соответствующие двойственные пары,
характеризующие процесс удовлетворения нужд потребителя
"проект-производство товара",
"сбыт-удовлетворение"
Крест производителя
трансформирует
потребности и запросы потребителя в конкретных товарах в их
производство, т.е. производитель осуществляет сопровождение процесса
удовлетворения нужд и запросов потребителей. таким образом, процесс создания
нужд и потребностей потребителей тесно взаимосвязан с процессами удовлетворения
нужд потребителей.
Таким образом, данный пример, характеризующий сферу удовлетворения нужд
потребителей (маркетинг), показывает, что эти процессы тесно
взаимосвязаны. А поскольку каждый этап такого процесса характеризуется
качественными характеристиками, то мы можем сделать однозначный вывод о том, что
между процессами удовлетворения нужд потребителя, характеризующимися
приведенными выше двойственными парами
"нужда-потребность",
"запрос-товар",
"проект-производство товара",
"сбыт-удовлетворение"
и двойственными парами, изображенными на рис.
2. существует однозначное соответствие.
Поэтому в самом общем случае создание
системы Управления Качеством может характеризоваться этапами
I. СОЗДАНИЕ СИСТЕМЫ
УПРАВЛЕНИЯ КАЧЕСТВОМ
1. Разработка Технического Задания (ТЗ).
2. Разработка нормативных стандартов Управления Качества.
3. Разработка системы Управления Качеством Технических средств и
Программного обеспечения.
4. Разработка системы Управления Качеством персонала.
II. СОЗДАНИЕ
СИСТЕМЫ СОПРОВОЖДЕНИЯ УПРАВЛЕНИЯ КАЧЕСТВОМ.
5. Сопровождение и корректировка нормативных стандартов Управления
Качества.
6. Сопровождение системы Управления Качеством Технических средств и
Программного обеспечения.
7. Сопровождение системы Управления Качеством персонала.
8. Оценка эффективности (степени удовлетворенности) системы Управления
Качеством.
2.
ОБ ОПТИМАЛЬНОМ УПРАВЛЕНИИ КАЧЕСТВОМ
Пожалуй, еще никто всерьез не обсуждал эту проблему. Не потому, что такой
проблемы не существовало. Просто не было возможности решать эту
проблему в самом общем виде.
Сейчас такая возможность уже существует. На страницах сайта обоснованы
Периодические законы Управления Качеством применительно в экономической
и социальной сфере. Здесь будет раскрыта методология создания
эффективной системы Управления Качеством.
2.1. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
Всеобщность Универсального
закона предполагает, что любые процессы, в том числе и процессы Управления
Качеством, являются периодическими (замкнутыми) и ограниченными определенным
числом устойчивых состояний. В Универсальном законе число устойчивых состояний
равно восьми.
Следовательно,
характеристику Качества любой системы можно давать в терминах
позиционной восьмеричной системы (рис. 3).
рис. 2
Если
тетраэдру с вершинами 1-4 сопоставить создание системы управления
качеством, то тетраэдр с вершинами 5-8 будет характеризовать сопровождение и
развитие системы управления качеством.
Если теперь в качестве альтернативных
двойственных перекладин креста выбрать двойственные пары
"нужда-потребность",
"запрос-товар",
то мы получим
крест потребителя,
характеризующий процесс возникновения потребительской нужды в определенном
товаре. Тогда крест производителя
будет характеризовать соответствующие двойственные пары,
характеризующие процесс удовлетворения нужд потребителя
"проект-производство товара",
"сбыт-удовлетворение"
Крест производителя
трансформирует
потребности и запросы потребителя в конкретных товарах в их
производство, т.е. производитель осуществляет сопровождение процесса
удовлетворения нужд и запросов потребителей. таким образом, процесс создания
нужд и потребностей потребителей тесно взаимосвязан с процессами удовлетворения
нужд потребителей.
Таким образом, данный пример, характеризующий сферу удовлетворения нужд
потребителей (маркетинг), показывает, что эти процессы тесно
взаимосвязаны. А поскольку каждый этап такого процесса характеризуется
качественными характеристиками, то мы можем сделать однозначный вывод о том, что
между процессами удовлетворения нужд потребителя, характеризующимися
приведенными выше двойственными парами
"нужда-потребность",
"запрос-товар",
"проект-производство товара",
"сбыт-удовлетворение"
и двойственными парами, изображенными на рис.
2. существует однозначное соответствие.
Поэтому в самом общем случае создание
системы Управления Качеством может характеризоваться этапами
I. СОЗДАНИЕ СИСТЕМЫ
УПРАВЛЕНИЯ КАЧЕСТВОМ
1. Разработка Технического Задания (ТЗ).
2. Разработка нормативных стандартов Управления Качества.
3. Разработка системы Управления Качеством Технических средств и
Программного обеспечения.
4. Разработка системы Управления Качеством персонала.
II. СОЗДАНИЕ
СИСТЕМЫ СОПРОВОЖДЕНИЯ УПРАВЛЕНИЯ КАЧЕСТВОМ.
5. Сопровождение и корректировка нормативных стандартов Управления
Качества.
6. Сопровождение системы Управления Качеством Технических средств и
Программного обеспечения.
7. Сопровождение системы Управления Качеством персонала.
8. Оценка эффективности (степени удовлетворенности) системы Управления
Качеством.
2.
ОБ ОПТИМАЛЬНОМ УПРАВЛЕНИИ КАЧЕСТВОМ
Пожалуй, еще никто всерьез не обсуждал эту проблему. Не потому, что такой
проблемы не существовало. Просто не было возможности решать эту
проблему в самом общем виде.
Сейчас такая возможность уже существует. На страницах сайта обоснованы
Периодические законы Управления Качеством применительно в экономической
и социальной сфере. Здесь будет раскрыта методология создания
эффективной системы Управления Качеством.
2.1. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
Всеобщность Универсального
закона предполагает, что любые процессы, в том числе и процессы Управления
Качеством, являются периодическими (замкнутыми) и ограниченными определенным
числом устойчивых состояний. В Универсальном законе число устойчивых состояний
равно восьми.
Следовательно,
характеристику Качества любой системы можно давать в терминах
позиционной восьмеричной системы (рис. 3).
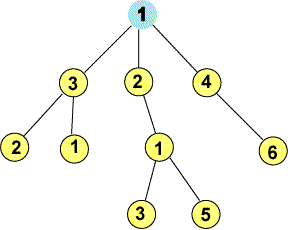
рис.
3
На этом рисунке приведены оценки подсистем Управления Качеством,
включая и подсистему высшего уровня. Из рисунка непосредственно видно, что
система Управления Качеством системы является многоуровневой и
определяется структурой системы. Но как определить интегральную оценку
Качества, имея совокупность абсолютных оценок Качества подсистем?
Ответ очевиден. Необходимо перейти к
относительным оценка Качества. Такие оценки можно получить как отношение
абсолютной оценки к основанию позиционной системы счисления. В нашем случае мы
получим следующее дерево относительных оценок
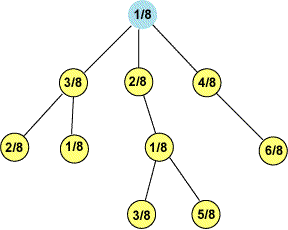
рис. 4
Такая форма отображения позволяет не только проводить оценки Качества
подсистем, но и для сравнительной оценки Качества разных подсистем между
собой, т.к. каждая оценка несет в себе не только количественную составляющую,
но и непосредственно характеризует и качественную сторону состояния процессов
Управления Качеством.
2.2. О НАДЕЖНОСТИ СИСТЕМЫ КАЧЕСТВА
Относительные оценки, характеризующие уровень Качества системы в каждом
ее процессе, позволяют получить, используя математический аппарат теории
надежности, уникальную возможность объективной оценки Управления Качеством как
для отдельных процессов, так и для всей системы в целом.
На всех этапах создание и сопровождение системы Управления Качеством
соответствует целевой функции системы- она направлена на
удовлетворение нужд и запросов потребителей и, следовательно, в самом понятии
Качество должны доминировать представления потребителей о компонентах Качества
("полезность"-"надежность", "стоимость-цена").
Поэтому само понятие
Качество будет являться многоуровневым, системным понятием, а главной
"перекладиной" рычага Качества, видимо следует считать надежность. Но и
надежность также является системным понятием. Так,
например, в технике это понятие в большей мере ассоциируется с надежностью ( бездефектностью, безотказностью), в то время как, например, в социологии
понятие надежность социальных отношений будет принадлежать уже к другому
"измерению", учитывающему уже не механистические, а социальные (человеческие)
факторы надежности.
Поэтому термин
"надежность" мы будем ассоциировать с Качеством. Такая тождественность
вытекает из системного смысла Управления Качеством. Относительные оценки
Качества подсистем, играя роль показателей надежности этих подсистем.
позволяют проводить интегральные оценки надежности как отдельных ветвей
структуры системы, так и всей системы в целом.
Из теории надежности нам
известны выражения для оценки надежности для последовательного и параллельного
соединения подсистем.
Для последовательного соединения
это выражение будет иметь вид, при условии, что
оценки качества
подсистем P (i), i=1,n
формируются в цепочке независимо друг от друга,
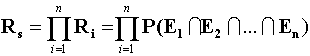
где
n - число последовательных
соединений.
Rs
-оценка
надежности системы качества,
Ei
- событие, состоящее в том, что подсистема имеет количественную
оценку качества (на стадии создания, сопровождения, сертификации).
Формула определяет правило умножения оценок качества системы.
Для параллельного соединения вероятность
оценки качества
всей системы будет оцениваться выражением
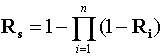
элементов в правой части характеризует
вероятность появления дефектов, сбоев и отказов в соответствующей подсистеме
Управления Качеством, составленной из n параллельных
ветвей.
В общем случае, при
последовательно-параллельном соединении подсистем качество будет
характеризоваться выражением для последовательного соединения подсистем,
каждая из которых может характеризоваться параллельным соединением входящих в
нее элементов качества.
Вот мы и получили
простейшие формулы оценки надежности (безотказности) системы Управления
Качеством, или просто оценки качества.
Так, используя эти
формулы, можно оценить Качество Управления для системы, приведенной на рис. 4.
Полученные формулы
можно усложнить, вводя соответствующие дифференциальные уравнения для
определения качества всей системы, вводя функции качества вида
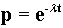
которая выбирается из условия, что подсистема имеет
оценку качества на интервале (t,t+dt), равную
величине 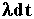 .
2.3. ОБ ОПТИМАЛЬНОЙ СТРУКТУРЕ СИСТЕМЫ УПРАВЛЕНИЯ КАЧЕСТВОМ
Получение выше выражения
для оценки Качества позволяют формально, с позиций теории надежности,
проводить оценку оптимальности структуры системы Качества.
Так,
последовательное соединение элементов подсистем Качества характеризуется
следующим графиком .
2.3. ОБ ОПТИМАЛЬНОЙ СТРУКТУРЕ СИСТЕМЫ УПРАВЛЕНИЯ КАЧЕСТВОМ
Получение выше выражения
для оценки Качества позволяют формально, с позиций теории надежности,
проводить оценку оптимальности структуры системы Качества.
Так,
последовательное соединение элементов подсистем Качества характеризуется
следующим графиком
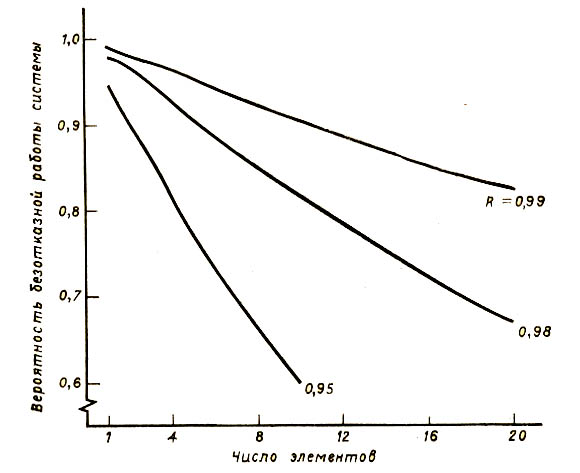
Рис. 5
Из этого рисунка видно, что при
последовательном соединении однотипных элементов, характеризующихся оценкой
качества R=0,99), качество системы зависит как от
числа таких подсистем, так и от их оценки качества. Отметим, что смысл оценки
R=0,99 определяет ее как интегральную оценку
надежности элементов, входящих в состав этой подсистемы.
Как можно видеть,
качество системы с последовательным соединением можно увеличить за счет
уменьшения числа последовательно соединенных подсистем и за счет повышения
качества каждого из них. При этом интегральная оценка качества системы
возрастает незначительно.
Очевидно, что с
увеличением числа подсистем качество системы уменьшается.
При параллельном соединении однотипных подсистем имеет место следующий график
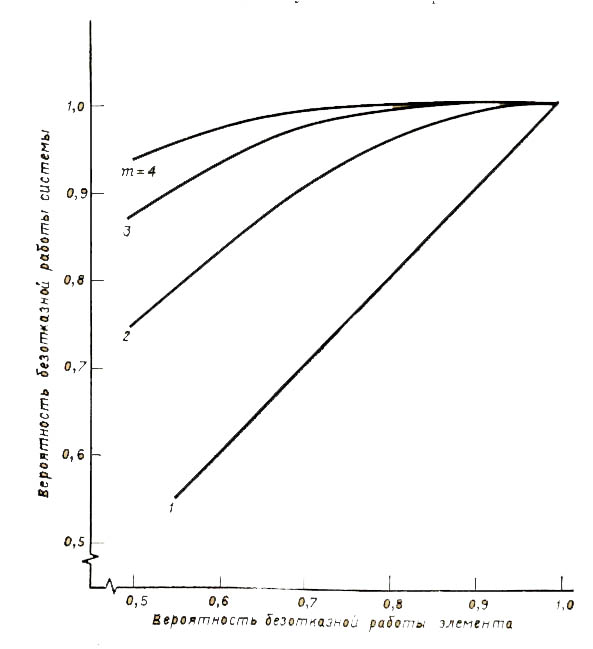
рис.
6
Из рисунка видно, что выигрыш в
качестве системы вследствие увеличения числа параллельно
соединенных подсистем растет все медленнее. На графике видно, что после
подключения четвертого параллельного соединения прирост качества системы
исключительно мал.
Поэтому, чаще всего. в практике теории надежности
находят большое распространение последовательно-параллельные способы
обеспечения надежности. Очевидно, что эти методы могут быть полностью
перенесены и на оценку систем качества.
2.4.
О МНОГОКРИТЕРИАЛЬНОМ СОБСТВЕННОМ ПРОСТРАНСТВЕ УПРАВЛЕНИЯ КАЧЕСТВОМ
При рассмотрении свойств собственных
пространств (основы теории
иерархии) были обоснованы свойства нормированных многокритериальных
собственных пространств поддержки решений и обоснован двойственный подход к
анализу и синтезу таких систем. исходя из тесной взаимосвязи структуры
(пространства) и функции (процесса).
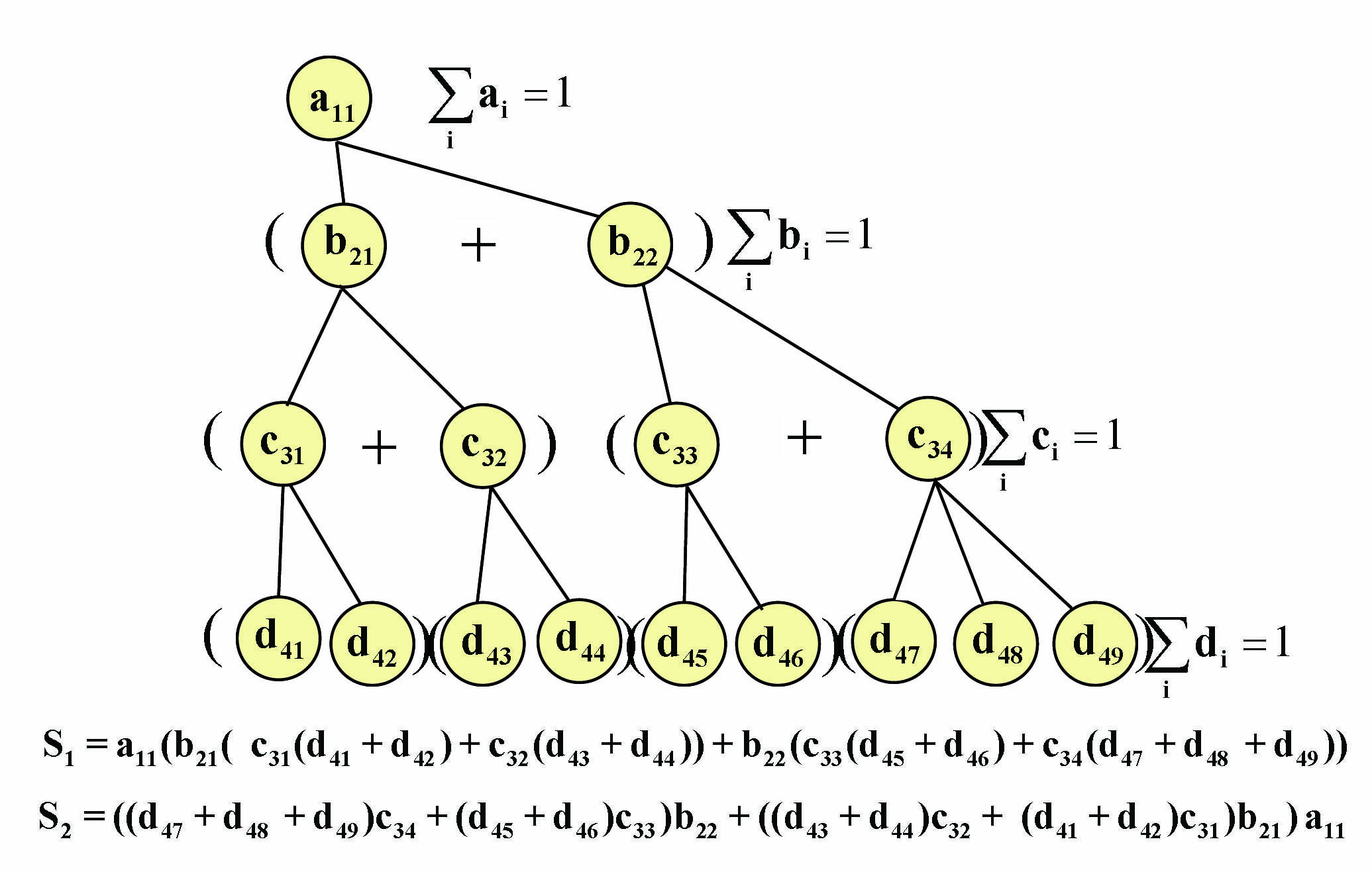 рис.
7
Нормировка показателей, характеризующих оценки качества целевых функций
вершин, позволяют подойти к оценке качества не только отдельных вершин, но и
всей системы в целом. Так, для нашей схемы, вводя относительные оценки качества
процессов вершин, мы получим, например, следующий структурный многочлен
S1=1(0,4(0,7(0,5+0,5)+0,3(0,9+0,1))+0,6(0,8(0,6+0,4)+0,2(0,3+0,3+0,4))
рис.
7
Нормировка показателей, характеризующих оценки качества целевых функций
вершин, позволяют подойти к оценке качества не только отдельных вершин, но и
всей системы в целом. Так, для нашей схемы, вводя относительные оценки качества
процессов вершин, мы получим, например, следующий структурный многочлен
S1=1(0,4(0,7(0,5+0,5)+0,3(0,9+0,1))+0,6(0,8(0,6+0,4)+0,2(0,3+0,3+0,4))
где значения относительных оценок
качества вершин равны следующим значениям
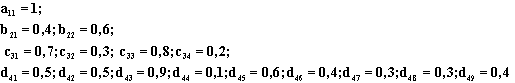 Относительные оценки качества могут отражать, и отражают, не только
количественную, но и качественную сторону процессов, протекающих в
многокритериальных системах. Более того, оценки качества процессов
(интегрированные и относительные, см.основы
теории иерархии), позволяют производить свертки и развертки
нормированных многокритериальных собственных пространств, в рамках
единого самосогласованного поля
целевой функции системы, без искажения ее системного
смысла на всех уровнях иерархии.
2.6. НОРМИРОВКА МНОГОКРИТЕРИАЛЬНЫХ ПРОЦЕССОВ
2.6.1. ПРИНЦИПЫ
СИНХРОННОСТИ И СИНФАЗНОСТИ
Каждая из вершин
иерархической структуры системы одновременно характеризуется строго
определенной целевой функцией (процессом), совокупность которых, в конечном
итоге порождает самосогласованное поле
целевой функции системы. От степени такой согласованности зависит качество
функционирования всей системы, синхронность и синфазность всех ее процессов и
подпроцессов.
Син-хронность.
Это слово применительно к собственным пространствам, означает, что
инвариантность преобразований одних собственных пространств в другие,
объединение собственных подпространств в пространства, предусматривает
совмещение их ритмов (частоты, вибраций). Каждое собственно пространство
характеризуется собственным временем, определяющим ритмы жизненного цикла
соответствующих систем, в рамках собственных пространств. Поэтому условие
синхронности при перенормировках, которые всегда должны происходить при
фазовых переходах из одного собственного пространства в другое, можно записать
в следующем виде
Относительные оценки качества могут отражать, и отражают, не только
количественную, но и качественную сторону процессов, протекающих в
многокритериальных системах. Более того, оценки качества процессов
(интегрированные и относительные, см.основы
теории иерархии), позволяют производить свертки и развертки
нормированных многокритериальных собственных пространств, в рамках
единого самосогласованного поля
целевой функции системы, без искажения ее системного
смысла на всех уровнях иерархии.
2.6. НОРМИРОВКА МНОГОКРИТЕРИАЛЬНЫХ ПРОЦЕССОВ
2.6.1. ПРИНЦИПЫ
СИНХРОННОСТИ И СИНФАЗНОСТИ
Каждая из вершин
иерархической структуры системы одновременно характеризуется строго
определенной целевой функцией (процессом), совокупность которых, в конечном
итоге порождает самосогласованное поле
целевой функции системы. От степени такой согласованности зависит качество
функционирования всей системы, синхронность и синфазность всех ее процессов и
подпроцессов.
Син-хронность.
Это слово применительно к собственным пространствам, означает, что
инвариантность преобразований одних собственных пространств в другие,
объединение собственных подпространств в пространства, предусматривает
совмещение их ритмов (частоты, вибраций). Каждое собственно пространство
характеризуется собственным временем, определяющим ритмы жизненного цикла
соответствующих систем, в рамках собственных пространств. Поэтому условие
синхронности при перенормировках, которые всегда должны происходить при
фазовых переходах из одного собственного пространства в другое, можно записать
в следующем виде
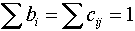 (*)
(*)
т.е.
сумма всех базисных измерений собственного пространства оказывается равной
единице, и.е. собственное пространство оказывается свернутым в точку.
Из смысла понятия следует, что синхронность характеризует только распределение
и перераспределение собственных значений между измерениями.
Син-фазность.
Относительные оценки, характеризующие качественно и количественно состояние
процессов, происходящих в той или иной вершине иерархической системы, еще не
гарантируют соблюдение условий автоматического нормирования всех
собственных подпространств. Необходимо, чтобы относительные оценки были
"сфазированы" жруг относительно друга, чтобы они отражали без искажений свой
собственный смысл.
Но
каким образом можно обеспечить синфазность измерений при фазовых переходах из
одного собственного пространства в другое? В этих
случаях для подпространств Сij необходимо
использовать ранжирование, т.е., например,
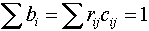 , ,
где
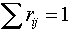 , ранг соответствующего измерения
j собственного подпространства i.
Поскольку Сij лежит в диапазоне 0-1, то
для любого собственного пространства иерархической системы будут
выполняться условия нормировки. Здесь относительные оценки несут в себе
информацию о фазе измерения, а ранжирование выполняет функции
определения интегральной относительной оценки, которая будет нести в себе
информацию о совокупной фазе всех измерений сворачиваемого в точку
собственного пространства. Поэтому, в общем случае, предыдущее равенство
превратится в неравенство , ранг соответствующего измерения
j собственного подпространства i.
Поскольку Сij лежит в диапазоне 0-1, то
для любого собственного пространства иерархической системы будут
выполняться условия нормировки. Здесь относительные оценки несут в себе
информацию о фазе измерения, а ранжирование выполняет функции
определения интегральной относительной оценки, которая будет нести в себе
информацию о совокупной фазе всех измерений сворачиваемого в точку
собственного пространства. Поэтому, в общем случае, предыдущее равенство
превратится в неравенство
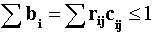
Эта разница характеризует
"дефект массы" собственного пространства. При движении к высшим
измерениям (свертка) "дефект масс" увеличивается, при движении к нисшим
измерениям (развертка) происходит высвобождение свернутых "масс",
восстанавливая первоначальный смысл измерений без искажений.
Из смысла синфазности
следует, что относительные оценки уже не характеризуют процессы
перераспределения собственных значений между измерениями собственного
пространства. Эти оценки, даже в их относительных величинах, имеют
собственные законы сохранения фазы процесса, характеризуемого целевой функцией
этого пространства и подпространства. Поэтому сумма относительных оценок всех
измерений таких подпространств далеко не всегда будет равна 1. Поэтому
понятно, что целевые функции собственных подпространств, с отношениями
субординации, должны быть согласованы. Именно в этом и заключается смысл синфазности измерений.
Относительные
оценки фаз измерений. Что представляет собой относительная оценка фазы того или иного измерения
собственного пространства? Каким образом можно
получить эту относительную оценку о фазе измерения?
Двойственность собственных пространств, проявляющееся в их структурном и
функциональном единстве, позволяет рассматривать каждое измерение как фазу
единого функционального процесса, определяемого целевой функцией этого
собственного пространства. Универсальный закон эволюции двойственного
отношения (монады) определяет все типовые фазы эволюции процесса эволюции
этого отношения. Следовательно, все относительные оценки, несущие информацию о
фазовых процессах в том или ином собственном пространстве, могут быть выражены
в позиционной системе счисления, с основанием 8, т.е. с использованием
относительных оценок Универсального закона. Эти оценки отражают не только
количественно состояние процесса, но и качественно, отражая его смысл (и
фазу).
Синхронность и синфазность способствуют
порождению феномена, который называется
голография.
Любая часть голографичных объектов содержит в себе весь объект,
без искажений смысла составляющих его элементов.
Эти важнейшие свойства нормированных собственных пространств (синхронность и
синфазность) могут стать основой для разработки цифровых голографических
моделей самых различных объектов, включая искусственный интеллект.
2.6.2.
СВЕРТКА И РАЗВЕРТКА МНОГОКРИТЕРИАЛЬНЫХ СОБСТВЕННЫХ ПРОЦЕССОВ
Как
мы уже отмечали, двойственность пространства и функции (каждой структуре
соответствует собственная целевая функция и наоборот, каждая целевая функция
обладает собственной структурой) позволяет свести задачу многокритериального
собственного пространства к задаче многокритериального собственного процесса.
При этом из самого понятие собственное пространство (или процесс)
непосредственно вытекает их самодостаточность. Свойство самодостаточности
собственных пространств позволяет осуществлять свертку и развертку
многокритериальных собственных пространств без искажения системного смысла.
2.7. ИНТЕГРИРОВАННАЯ ОЦЕНКА СОБСТВЕННЫХ
ПРОСТРАНСТВ
Интегрированным собственным пространством, характеризующим состояние того или
иного протекающего в нем процесса, будем называть пространство (процесс),
непосредственно включающее в себя рассматриваемый (анализируемый,
синтезируемый).
Смысл
интегральной оценки качества процесса
Wi=SaijSij
где
Wi
–
интегральная оценка качества процесса
aij
– ранг, характеризующий “вес”
относительной оценки j-го
подпроцесса в ингетральной оценке,
Saij=1.
Sij-относительная
оценка качества j-го
подпроцесса
Таким
образом, интегрированная оценка качества (фаза) процесса агрегирует все
подчиненные ему процессы в единый процесс, характеризуя свертку собственного
n-мерного
подпространства в точку. С точки зрения интегрированного процесса
интегрированная оценка процесса характеризует некую усредненную фазу этого
процесса.
Обоснованные выше свойства Универсального закона, отражающие периодичность,
преемственность, ограниченность и замкнутость процессов эволюции двойственных
отношений, позволяет подойти к оценке качества процессов как оценки фазового
состояния многоуровнего процесса, используя единую шкалу относительных оценок
Универсального закона.
2.8.
НОРМИРОВАННЫЕ И АВТОНОМНЫЕ
ПРОЦЕССЫ
Это
ПРОЦЕССЫ, свернутые в точку,
интегральная оценка качества которых приводится к нормализованному виду,
определяемому с помощью нормирующего множителя
ki=1/Wi
Умножая все относительные оценки качества нормируемого процесса на этот множитель, мы приводим этот процесс к интегральной оценке,
равной 1.
Нормированные
процессы формируются путем умножения всех относительных оценок качества этого
процесса на нормирующий множитель
ki.
Нормированные процессы, обладая самодостаточными целевыми функциями, могут
“подключаться” к интегрировавшим их процессам и корректировать интегральную оценку
(точку) только в случае выхода текущей интегрированной оценки качества
нормированного
процесса за рамки допустимых значений. Такие нормированные процессы будем
называть автономными.
Автономные процессы могут быть
активированными и не активированными. При неактивированном состоянии
интегрирующий процесс не связан с автономным. Поэтому
автономный процесс является расфазированным.
Фазировка автономных процессов и подпроцессов.
Заключается в активации автономного процесса. Для этого
производится перерасчет всех оценок качества этого автономного процесса,
получается текущая относительная оценка качества активированного
процесса (подпроцесса), которая затем умножается на интегрированную оценку этого
процесса, полученную при последней активации автономного процесса.
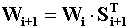
где
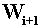 -новая интегрированная оценка качества процесса,
-новая интегрированная оценка качества процесса,
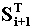 -
текущая относительная оценка качества автономного процесса, -
текущая относительная оценка качества автономного процесса,
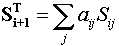 -совокупность относительных оценок качества автономного
процесса.
-совокупность относительных оценок качества автономного
процесса.
 -
интегральная оценка качества процесса, полученная при предыдущем
активировании процесса.
Перевод актированного автономного процесса в дезактивированный производится
путем умножения на новый нормирующий множитель -
интегральная оценка качества процесса, полученная при предыдущем
активировании процесса.
Перевод актированного автономного процесса в дезактивированный производится
путем умножения на новый нормирующий множитель
ki+1=1/Wi+1
Только в
этом случае обеспечивается автоматический пересчет интегрированной и
относительной оценок качества без искажения системного смысла исходного
процесса при активации и дезактивации автономных процессов.
2.9.
СХЕМА ВЗАИМОДЕЙСТВИЯ МЕЖДУ ПРОЦЕССАМИ
Интегрированные и относительные оценки качества процессов, протекающих в
многокритериальных собственных пространствах позволяют получать не только
количественные но и качественные результаты.
При этом многокритериальные пространства процессов, характеризуемых только
синхронностью, т.е. характеризуют только динамику процессов, только
распределение и перераспределение ресурсных потоков, то в таких задачах
системный смыл будет сохраняться всегда. В таких системах можно положить, что
относительные оценки качества всех ранжированных показателей качества
равны 1, а сами показатели качества ранжированы в соответствии со степенью
своего вклада в качество соответствующего нормированного процесса.
Многокритериальные пространства, в которых наряду с динамикой процессов удается
отлеживать и их фазовое состояние, обладают свойствами «голографичности»,
которое немыслимо без сохранения фазы регистрируемых сигналов.
голографичность=син-хронность
+ син-фазность
Единый закон эволюции двойственных отношений , характеризуя ограниченный и
замкнутый набор фазовых состояний процессов, позволяет использовать для оценки
их качества номерами вершин многоугольника решений целевой функции этого
двойственного отношения, т.е. достаточно определить соответствие между процессом
и номером вершины устойчивой фазы его состояния и мы тем самым получим оценку
качества процесса, отражающую и количественную и качественную сторону процесса.
В
реальных многокритериальных системах протекающие в них процессы обладают
свойствами адаптивности. Это означает, что реальная система постоянно
изменяет свои функции и структуру.В ней постоянно идут процессы интеграции и
дифференциации. В результате в системе постоянно возникают нарушение
синхронизации и
синфазности нормированных
процессов и подпроцессов. При нормальном режиме функционирования процессов все
агрегированные процессы и подпроцессы функционируют автономно, т.е. являются
автономными.
При возникновении недопустимых отклонений
автономные процессы активируются. Происходит фазировка автономного процесса с
интегрированным процессом с последующей корректировкой интегрированной оценки
этого нормированного процесса. При восстановлении допустимых ограничений на
интегральную оценку подпроцесса, последний снова может быть
переведен в разряд автономных (дезактивирован).
Таким образом, рассмотренный поход к Управлению Качеством многокритериальных,
нормированных собственных процессов, в основе которого лежат естественные
механизмы нормировок и перенормировок собственных пространств ( процессов)
позволяют самым естественным образом определять интегральные и относительные
оценки качества этих процессов, без искажения
системного смысла их целевых функций. Подобный подход позволяет обосновать
новые подходы в Управлении Качеством.
РЕЗЮМЕ
1. Единый
Универсальный закон позволяет создать единую методику оценки систем
Управления Качеством, независимо от их природы и оптимизировать их структуру
на основе новой Теории Управления Качеством.
2. В основу
Теории Управления Качеством
могут быть по праву положены математические методы, разработанные в рамках
теории надежности, математической статистики, исследования операций и других
приложений, где используются вероятностные оценки. Однако применительно
к теории Управления Качеством эти вероятностные оценки будут иметь
реальный смысл относительных оценок качества, которые могут использоваться для
сравнительных оценок любых систем, независимо от их природы.
3.Ниже, на страницах
сайта, при рассмотрении проблем качества в сфере социологии, экономике,
будут дополнительно рассмотрены отдельные проблемные вопросы Управления
Качеством с позиций Единого Универсального закона, включая обоснование
соответствующих Периодических законов.
e-mail:
С
благодарностью приму все ваши замечания, предложения,
с признательностью отвечу на ваши вопросы
|

 "Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг). М.И. Беляев, 2015г,©
"Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший разум, ченнелинг). М.И. Беляев, 2015г,©