5.4.2.1.2.Оболочки

 

Главная Вверх 
          "Каждая цивилизация в определенном возрасте имеет возможность возвысить, или разрушить себя. Если делается выбор в пользу возвышения, то возникает импульс, позволяющий появиться учениям об утерянных законах сущего".   (Высший разум, ченнелинг).   
                                                                            М.И. Беляев, 2015г,©
 
СВОЙСТВА МОНАДНЫХ КРИСТАЛЛОВ И ИХ ОБОЛОЧЕК
 
1. ОБ АУРЕ  ЖИВЫХ И МЕРТВЫХ   МОНАДНЫХ КРИСТАЛОВ
        Из вышеизложенных свойств монадных кристаллов можно сделать вывод о том, что "заряженные" триангулы (или триангуляры) являются источником движения и могут порождать как мертвые (статические), так и живые (динамические) кристаллы.
        Известно, например, следующее высказывание гениального физика Николы Тесла:
"В кристалле мы имеем ясное доказательство существования общего принципа жизни, и хотя мы не можем понять жизни кристалла, тем не менее он - живая субстанция".
Кристаллы (и живые, и мертвые) способны к запоминанию, хранению  и передаче информации. И они это могут осуществлять вполне самостоятельно, без вмешательства человека. Поэтому даже мертвые кристаллы следует называть скорее живыми, чем мертвыми. Поэтому, даже мертвые кристаллы можно называть формой жизни, пусть примитивной, но жизни. Так, кристаллы растут, дают потомство, чутко откликаются на воздействия и даже с успехом к ним приспосабливаются. Они могут обладать даже способностью к регенерации своих утраченных частей. Вокруг себя кристалл активно формирует собственное поле-ауру, подобно ауре любого живого организма. Но эта аура является так, сказать "тонкой оболочкой" кристалла. Однако любой кристалл имеет и физические оболочки.
    Любой монадный кристалл, уже в силу определения, является двойственным. В соответствии с концепцией "атомизма", рассмотренной на страницах сайта (подробнее), любой монадный кристалл можно представить в виде внешней оболочки и ядра. Так, в монадном Цветке Жизни внешней активной оболочкой будут служить система внешних "лепестков", а ядром - внутренний (центральный )  лепесток Цветка.  Это происходит в силу оболочечного строения монадных кристаллов. И эти свойства находят отражения  в живых организмах, во флоре и фауне планеты.
         Так, например,  у деревьев только самый внешний слой является активным, жизнедеятельным. А любой атом, любой кристалл имеет собственную ауру. У мертвых кристалов эта аура холодная, спокойная, неподвижная. У живых кристаллов эта аура динамична. Она может цвести всеми цветами радуги. И эти свойства должны находить отражение в монадной Цветке Жизни.
 
 
  
 
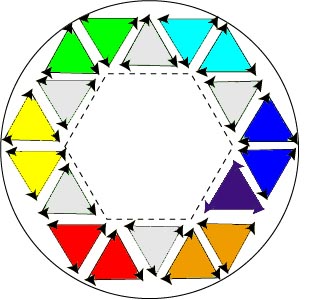                                                                 Рис. 1
        На приведенном рисунке приведены примеры структуры внешних оболочек монадных кристаллов, или ауры  монадного кристалла, или монадного Цветка.
    Верхние рисунки отражают замкнутую двойную спираль живой оболочки (ауры), внутренний и внешний слой которой вращаются в одном направлении. Поэтому  цепочки  двойной спирали построены из триангул с противоположными спинами. Правый верхний рисунок иллюстрирует принципы порождения частиц, со свойствами цветов радуги. Если эти частицы  отождествить с музыкальными нотами, то промежуточные триангулы, стоящие между основными тонами (нотами), будут характеризовать полутоны. Эта внешняя оболочка обладает фильтрующими свойствами. Она обладает системой  входных и выходных "пор", соединяющей внешнюю среду  с внутренней структурой кристалла.
    На нижних рисунка приведен пример ауры  мертвых кристаллов. Эта аура характеризуется статикой, хотя ее оболочка и имеет систему входных и выходных "пор". Оболочка ауры оказывается незамкнутой ("пустая" триангула, сопряженная с соседними в противофазе).
  Из  вышеприведенных примеров внешних оболочек кристаллов и их ауры можно сделать вывод о том, что  внешние оболочки монадных кристаллов, взаимосвязанные с внутренней структурой монадного кристалла, отражают и также и свойства своей ауры. Например, монадные кристаллы с "вращающейся" внешней оболочкой будут формировать подобную двойственную ауру, со свойствами "статор"-"ротор".
Оболочечное строение монадных кристаллов позволяет природе осмысленно строить новые оболочки, понять причины возникновения искажений в кристаллических решетках (дислокаций). Подобные дислокации могут возникать в результате незамкнутости силовых линий  монадной оболочки. Возникновение такой триангулы в структуре  не только искажает структуру монадной оболочки, но и способствует тому, что новая монадная оболочка начнется строиться в противофазе (новый виток).
         Такая триангула способствует формированию ленты Мёбиуса, осуществляя переход с одной перекладины монадного животворящего креста к его другой перекладине. А что, если в этой оболочке убрать одну секцию (корпускулу)?
                                                         рис. 2-1
         Из рисунка видно, что в данной монадной оболочке царит гармония. Ниже будет показано,  что пятизвездочные и шестизвездочные оболочки (и кристаллы) тесно между собой взаимосвязаны. Они взаимодополнительны.         
 На следующем рисунке  приведен пример эволюции цветов радуги.
           
                                                                рис. 2-2
      Посмотрите, как последовательно в каждом секторе гексады идет эволюция цветов и как гармонично стыкуются друг с другом сектора, формируя целостные взаимодополнительные  монады. Заметьте также,  что в каждой  триаде в этом шестиугольнике являются одноименными триграммами И-Цин и что вращение этих триад возможно в противоположном направлении.
       В приведенном рисунке  взаимосвязи составления таким образом, что все триады оказываются  взаимно уравновешенными и формируют статический шестигранный кристалл.
 Если в следующем шестиугольнике мы сменим взаимосвязи на противоположные и соединим с первым, то мы снова получим статическую  картину взаимодействия.
         Но ситуация кардинально переменится, если мы соединим триады таким образом, чтобы их векторы устремлений совпадали. В этом случае мы тоже получим гармоническую картину, но она будет отображать уже  "живой" (динамический) кристалл. Здесь каждые три цвета, смешиваясь будут формировать собственную радугу.
       Голографическая подобность  собственных пространств радуги  позволяет говорить о том, что гармонию радуги музыки и радуги цветов можно распространить и на другие миры вселенных.     
 
2. О МОНАДНЫХ ОПЕРАТОРАХ
     О способности кристаллов воспринимать, хранить и передавать информацию ученым уже хорошо известно.
С точки зрения математики для работы с монадными кристаллами,  для формирования их внешних оболочек можно использовать существующий математический аппарат (теория групп, матричные, векторные методы, и т.д.). Мы рассмотрим только некоторые основные правила манипулирования с этими операторами. Выбирая тот или иной оператор, например, одну , две, или три триангулы, сопряженные между собой определенным образом, мы можем получить следующие замкнутые оболочки  (рис. 3).
 
 
 
 
 
 
 
 
 
 
 
 
Рис. 3
          Эти операторы используются следующим образом. Вначале оператор копируется (самовоспроизведение). Затем поворачивается на определенный угол (600) и приклеивается к концу цепочки. Не напоминает ли это правила формирования элементарных частиц (мезонов и барионов)? Анализ свойств монадных оболочек и монадных операторов позволяют сделать вывод о том, что именно монадные операторы порождают замкнутые монадные оболочки (семейства монадных частиц), формируя целостный монадный кристалл (монадный Цветок Жизни). Монадные операторы (и соответствующие монадные оболочки) могут характеризоваться вложенной структурой.
 
        Рис. 4 
        На рис. 4 показаны три вложенные друг в друга монадных оболочки, сформированных монадными операторами I, II, III. Желтым цветом обозначены триангулы, векторы устремлений которых направлены по часовой стрелке, а голубым -против часовой.
Полученный  монадный Цветок обладает многими замечательными свойствами.   Отметим только некоторые из них.
        1. Оператор II  составлен  из триангул с противоположной спиральностью. Особенность  монадной оболочки, построенной с использованием данного оператора заключается в том, что между ттаким "шестеренками" возникает необходимость вставить дополнительную. Иначе единую цепочку просто не сформировать. Одноименные полюса диполей будут отталкиваться друг от друга, а дополнительная "шестеренка", играя роль изолятора, их склеивает в единую монадную цепочку. Эти шесть триангул, при сопряжении с  монадной оболочкой I, распадаются на две триады. Одна нейтральная, а другая - заряженная. Эту подоболочку можно назвать резонансной.
        2. Оператор III составлен  из трех триангул. Две из них имеют одну спиральность, а третья -противоположную. Полученная оболочка представляет собой удвоенную цепочку, скрученную в спираль. При сопряжении этой монадной оболочки с предыдущей, вектора устремлений на соприкасающихся ребрах имеют противоположные знаки. Это приводит к тому, что оболочки жестко склеиваются в единый монадный кристалл, имеющий между собой общую систему входных и выходных "пор". Внешняя оболочка полученного кристалла является "демократичной". Она не отторгает поступающую в кристалл информацию, а "переваривает" ее в кристалле и через систему  выходных пор удаляет "шлаки".
        3. Ниже будет показано, что супермультиплеты элементарных частиц обладают таким же свойствами, как и данный монадный Цветок.
    Используя в качестве монадных операторов химические соединения, способные образовать замкнутые цепочки, можно получать различные типы кристаллическихрешеток и моллекуоярные структуры, в соответствии с правилами"обхода по кресту" и порождения частиц. 
           рис. 5
           Например, бензольное кольцо (химия) можно представить в виде следующего монадного кристалла
            рис. 6
            Из  этой формы видно, что свободные валентные связи могут оказаться упорядоченными, способными к обобществлению  6 электронов, заставляя их вращаться вокруг обшей оси симметрии кристалла. Будет ли такая форма соответствовать действительности, или такая форма будет трансформирована в иную, под влиянием обобществления электронов?
    Говоря о монадных оболочках, нельзя не сказать о Платоновых телах, о свойствах которых говорится  на странице  "Монадные формы", сотканных из треугольников.
         Особое внимание следует уделить соотношениям, которые отражаются в Платоновых телах. Это соотношение характеризуется рядом Фибоначчи <1,1,2,3,5, 8,13,21,..>.
      При рассмотрении свойств священного календаря майя был рассмотрены  его оболочки
                                         
                                                                        Рис. 7
       Оболочки этого календаря, характеризуемые отношениями 8:13:20, отражают Циклы Законов Абсолюта (О календаре майя, Календарь 13 лун, Законы Абсолюта ).
3. О МОНАДНОЙ  ФИЗИКЕ
    3.1. О ПРОИЗВОДЯЩИХ ФУНКЦИЯХ
    Векторы устремлений,  монадные операторы, свойства которых рассмотрены выше, позволяют  утверждать, что монадные оболочки природа строит не как попало, а использует определенные математические правила, определенные математические методы. Пожалуй, к самым  уникальным математическим функциям, порожденных монадными операторами, можно отнести производящие функции. Из математики известно, что всякий раз,  когда необходимо получить информацию о последовательности чисел <a0,a1,a2,...>, мы можем образовать бесконечную суму по степеням  параметра  "х"
т.е. производящую функцию для исходной числовой последовательности. Если эта последовательность определена интуитивно, т.е. если  an  определяется  по <a0,a1,a2,...>, то это дает важные преимущества при исследованиях. Многие поколения математиков в своих исследованиях использовали производящие функции. часто даже не заботясь о проблеме сходимости таких бесконечных сумм, поскольку вначале цель исследования заключатся  в поиске возможных подходов к решению той или иной задачи. Когда такое решение будет найдено, любым методом, каким бы не строг он ни был, можно потом всегда независимым способом убедиться в верности такого решения. Поэтому производящие функции, использующие в качестве параметра "х" тот или иной монадный оператор, позволяют описывать свойства тех или иных монадных оболочек.
 
3.2. ЧЕТНЫЕ И НЕЧЕТНЫЕ МОНАДНЫЕ ПРОИЗВОДЯЩИЕ ФУНКЦИИ
    Из математики известно, что бесконечные суммы могут образовывать четные и нечетные производящие функции, т.е. параметр "х" в таких рядах будет иметь соответственно или четные или нечетные значения. Тогда, задавая в качестве параметра "х" одну из базисных экспоненциальных  функций  eix ,e-ix,-e-ix,-eix, и выбирая монадный оператор, порождающий четную и нечетную цепочки экспоненциальных функций. мы получим следующие монадные нечетные и четные оболочки и подоболочки.
1. Используя в качестве единичного монадного оператора , мы получим следующую последовательность монадных подоболочек  и оболочек
    Заметим, что данная матрица, дополненная сопряженными членами, отражает структуру подоболочек Периодической системы химических элементов, которая характеризуется последовательностью <1,3,5,7>. Последовательное суммирование (сворчивание) подоболочек порождает числовую последовательность <1,4,9,16>, т.н. порождает числовую последовательность. характеризующих систему Боровских орбит в  атоме  водорода. Сворачивание подоболочек в оболочки,  которое осуществляется простым суммированием соответствующих строк и столбцов данной матрицы, порождает числовую последовательность, характеризующую структуру Периодической системы химических элементов,  которая получается путем удвоения ряда <<1,1>,<4,4>,<9,9>,<16,16>>.  Оказывается, что экспоненциальная функция  производящая функция описывает свойства монадных частиц всех монадных семейств. Параметр "х" каждой монадной частицы получается с использованием следующего монадного оператора
т.е. экспоненциальная монадная цепочка оказалась квантованной. Если теперь взять в качестве кванта, вместо   функцию , то мы сразу получим следующую четную последовательность <2,6,10,14>, сворачивание которой порождает последовательность <2,8,18,32>.
    Таким образом, используя  экспоненциальные производящие функции для порождения монадных оболочек, мы непосредственно придвинулись  к химии и физике.
 
3.3.  О ГЕНОТИПЕ ПРОИЗВОДЯЩИХ ФУНКЦИЙ ОБОЛОЧЕК
    На странице "Геном памяти" приведен следующий рисунок,  отражающий  схему формирования ГЕНОМА, сотканного из операторов экспоненциальных функций.
                      
                                                                     рис. 8
        На странице "Преемственность" мы отмечали двойственность функций, порождаемых операторами, формирующими производящий крест ГЕНОМА.
 
                                        
                                                                               рис. 9
 
       Отметим важную особенность "обхода по кресту". Здесь  ЗАПРЕЩЕНЫ операторы
                                                             G0<->P1  и   G1<->P0 .
Если теперь отождествить  эти 4 "первокирпичика" с аналогичными первокирпичиками, из которых плетутся двойные спирали ДНК, то мы получим феноменальные совпадения.
     Существуют ТОЛЬКО четыре (!!) типа азотистых оснований: аденин и гуанин    (азотистые   основания  пуринового   ряда),   тимин   и  цитозин    (основания пиримидинового ряда). Их сокращенно обозначают    по начальным буквам: А, Г, Т, Ц. Каждая горизонтальная «перекладина» содержит либо аденин и тимин (А—Т или  Т—А), либо гуанин и цитозин (Г—Ц или Ц—Г).
          Соединения аденина с гуанином (А-Г), а также тимина с цитозином (Т-Ц) не реализуются.
      Мы видим, что в производящих функциях зависимости совершенно аналогичные.
     Поэтому, сопоставляя G0=Т,    P0 =A,  P1 =Ц,   G1=Г, мы видим полное совпадение механизмов формирования производящих функций и механизмов формирования молекул ДНК.

  Функции   Gn(x) и Pn(x)   являются двойственными

        Так, функция Gn(x)=(1-x)-n (1+x), n=1,2,3,..    порождает многочлены                

                                             G0(x)=1+2x+2x2+2x3+ ...

                                             G1(x)=1+3x+5x2+7x3+  ...                   

                                             G2(x)=1+4x+ 9x2+16x3+ ...

                                             G3(х)=1+5х+14х2+30х3

в то время как функция

                                    Gn(x)=(1+x)-n (1-x), n=1,2,3,....      порождает многочлены с иными свойствами        

                                              G0(x)=1- 2x+ 2x2-2x3+ .. 
                                              G1(x)=1-3x+5x2- 7x3+...           
                                               G2(x)=1-4x+9x2-16x3+...
                                               G3(x)=1-5x+14x2-30x3+ ...
     Функции Pn(x) также являются двойственными и для них также справедливы аналогичные соотношения.
    Если теперь в качестве параметра "х" бесконечной суммы ряда  принимать базисные экспоненциальные функции, то мы придем к осознанию ЕДИНСТВА производящих и экспоненциальных функций.
   Для этого в базисных операторах производящих функций
                               
 следует просто заменить параметр  "х" на параметры базисных экспоненциальных функций вида  "eix".      В этом случае матрица И-Цзин (рис. 8), формируемая двойными спиралями  производящих функций с экспоненциальными параметрами,  будет формировать ЕДИНОЕ САМОСОГЛАСОВАННОЕ ПОЛЕ ГЕНОМА МИРОЗДАНИЯ.
 
4. ОБ ЭНЕРГЕТИКЕ МОНАДНЫХ КРИСТАЛЛОВ
        На рис.20 приведены три триангулы, которые  отличаются друг о друга   тем, что внутренний кристалл в каждой триангуле сдвинут по фазе 1200 относительно  предыдущего кристалла. В результате такого поворота свойства всех трех триангул оказываются разительно различными.
    Рис. 10
        Так, в первой триангуле все "поры" являются или входными, или выходными. Во второй, и в третьей - из трех "пор" работает только одна, но не одна и та же. К аналогичным результатам приводят и повороты других  внутренних триангул. В конечном итоге эти повороты будут сказываться на энергетическом балансе монадных оболочек. В одном случае она может поглощаться, а в другом, преимущественно излучаться.
 
РЕЗЮМЕ
        1. Рассмотренные на данной странице  свойства монадных кристаллов не являются реальной действительностью. Они являются монадной моделью, отражающей только самые существенные грани и свойства этой реальности, вытекающие из Универсального закона. Реальность эти модели могут приобретать тогда, когда, например, будет рассматриваться только какая-либо одна из 26 конкретных монадных форм отраженных в монадном Цветке Жизни. Так, Периодическая система химических элементов содержит в себе структуру всех химических элементов, но не является реальным кристаллом. В кристалл  она трансформируется тогда, когда начинает отражать свойства одного из атомов, входящих в общую структуру монадного Цветка Жизни химических элементов.
    2.Кварковые кристаллы, характеризующие классификации семейств элементарных частиц, вскрывают изначально кристаллические принципы строения живой и неживой материи
      3.  Анализ свойств мужского и женского монадного кристалла позволяет сказать, что внешняя оболочка женского кристалла  характеризуется "эмоциями", при внутренний "невозмутимости", а у мужского, наоборот, под внешней невозмутимостью скрываются бурные эмоции.
       4. В женском кристалле царит двойственность-уравновешенность достигается за счет объединения триангуляров с противоположным направлением векторов устремлений, в то время как в мужских кристаллах происходит объединение триангуляров с одним и тем же  направлением векторов устремлений.
    5. Поскольку атомы химических элементов и их соединений характеризуются  наличием кристаллической решетки, то, может быть, свойства мужских и женских монадных форм поможет, наконец, понять природу возникновения на их поверхностях, при натирании, положительных и отрицательных зарядов? 
     6. Может быть свойства мужских и женских монадных кристаллов помогут лучше понять природу и причины возникновения дислокаций в кристаллах и их рост по спирали (ступеньками)?
 
                                    
e-mail:

     С благодарностью приму все ваши замечания, предложения,
                     с признательностью отвечу на ваши вопросы
 
 
    © Беляев М.И., "МИЛОГИЯ", 2015г.
 Опубликован: 26/10/2013г., обновлен: 02 октября 2014.
           Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать  о всех замеченных ошибках, некорректных формулировках.
         Книги "Основы милогии", "Милогия" могут  быть высланы в Ваш адрес наложенным платежом,
  

Карта сайта

rss
Карта