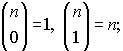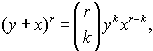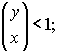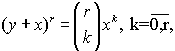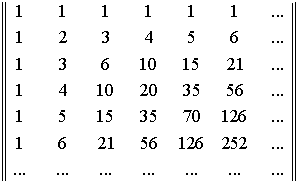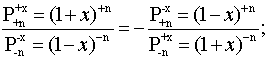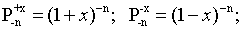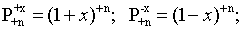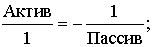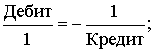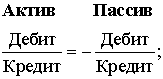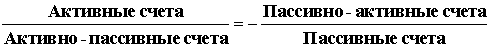ЗАКОНЫ СОХРАНЕНИЯ
СИММЕТРИИ
И ГЕНЕТИЧЕСКИЙ КОД
1.
РУССКАЯ МАТРИЦА ЗАКОНОВ СОХРАНЕНИЯ СИММЕТРИИ
Законы сохранения симметрии лежат в основе Единого закона эволюции двойственного
отношения.
Необходимо
осознать, что
ЗАКОНЫ
СОХРАНЕНИЯ СИММЕТРИИ НИКОГДА НЕ НАРУШАЮТСЯ:
НАРУШЕНИЕ
ОДНОЙ ФОРМЫ СОХРАНЕНИЯ СИММЕТРИИ, ПОРОЖДАЕТ ДРУГУЮ ФОРМУ СОХРАНЕНИЯ СИММЕТРИИ.
При
этом зеркальная форма симметрии (С-инвариантность)
может трансформироваться в зарядовую форму сохранения симметрии (Р-инвариантность).
При
этом возникает комбинированный закон сохранения симметрии (СР-инвариантность).
Из физики известно, что данный комбинированный закон является почти абсолютным,
т.е. почти никогда не нарушается.
И, наконец, существует абсолютный закон сохранения симметрии, который никогда не
нарушается.
Это комбинированный закон сохранения симметрии СРТ-инвариантности,
за которым скрывается комбинация
трех симметрий (С-инвариантность,
P-инвариантность и
T-инвариантность).
Этот закон сохранения имеет особое значение для понимания
механизма инвариантных преобразований из одного собственного подпространства
(пространства) в другое, то есть
инвариантности
по отношению к
одновременному
выполнению
трех операций –
замене частиц
на
античастицы,
зеркальному
отражению и
обращению
течения
времени.
Обратите
внимание, речь идет не о направлении течения времени вспять. Речь идет
о тождестве
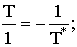 Аналогичное тождество можно
записать теперь и для закона сохранения СРТ-инвариантности.
Аналогичное тождество можно
записать теперь и для закона сохранения СРТ-инвариантности.
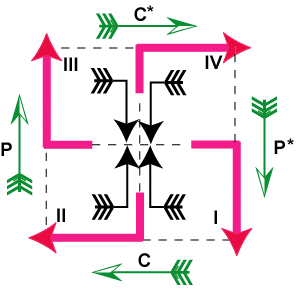
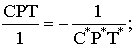 рис. 1
Из рисунка 1 можно
увидеть, что вектор С-инвариантности и Р-инвариантности по отношения друг к
другу являются инвариантными, т.е. данное утверждение можно записать в
векторной форме
рис. 1
Из рисунка 1 можно
увидеть, что вектор С-инвариантности и Р-инвариантности по отношения друг к
другу являются инвариантными, т.е. данное утверждение можно записать в
векторной форме
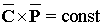 Из этого векторного уравнения можно
непосредственно получить более общее, отражающего Суть Единого Поля законов
сохранения симметрии.
Из этого векторного уравнения можно
непосредственно получить более общее, отражающего Суть Единого Поля законов
сохранения симметрии.
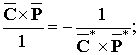 При этом изменение одного поля приводит к
изменению другого (природный принцип саморегулирования).
При этом изменение одного поля приводит к
изменению другого (природный принцип саморегулирования).
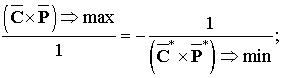
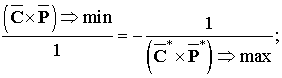 А теперь вспомним
векторное уравнение электромагнитного поля
А теперь вспомним
векторное уравнение электромагнитного поля
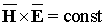 Векторы магнитной
(H)
и электрической (Е)
напряженности ортогональны друг другу, при этом изменение вектора
магнитной напряженности приводит к соответствующему изменению вектора
электрической напряженности.
Векторы магнитной
(H)
и электрической (Е)
напряженности ортогональны друг другу, при этом изменение вектора
магнитной напряженности приводит к соответствующему изменению вектора
электрической напряженности.
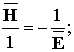 Это тождество в графической форме можно отражается следующим образом.
Это тождество в графической форме можно отражается следующим образом.
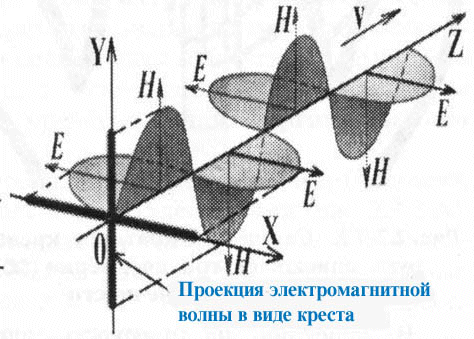 рис.
2
Таким
образом, из рис. 2 следует непосредственный вывод о полной аналогии
между полем законов сохранения симметрии и электромагнитным полем.
рис.
2
Таким
образом, из рис. 2 следует непосредственный вывод о полной аналогии
между полем законов сохранения симметрии и электромагнитным полем.
 рис. 3
Фундаментальность этих тождество
означает, что отныне теория электромагнитного поля может быть применима не
только к физике, а вообще к любой сфере научной и общественной деятельности.
2. РУССКАЯ МАТРИЦА
ГЕНЕТИЧЕСКОГО КОДА
Существуют всего четыре
(!!) типа
азотистых оснований: аденин
и гуанин
(азотистые основания пуринового ряда), тимин
и цитозин
(основания пиримидинового ряда). Их сокращенно обозначают по
начальным буквам: А, Г, Т, Ц.
Каждая горизонтальная «перекладина»
содержит либо аденин и тимин (А-Т
или Т-А), либо
гуанин и цитозин (Г-Ц
или Ц-Г).
Соединения аденина с гуанином (А-Г),
а также тимина с цитозином (Т-Ц)
не реализуются.
Считается,
что определенное чередование пар
А- Т,
Т-А,
Г-Ц
и
Ц-Г
вдоль «лестницы» и есть генетический код,
фиксирующий индивидуальность данного живого организма. Несмотря на то что
используются только четыре типа «перекладин», огромное количество этих
«перекладин» на «лестнице» позволяет записать в молекуле ДНК всю наследственную
информацию.
Двойная спираль ДНК позволяет высказать предположение о том, что эти спирали
формируются двумя животворящими крестами, составленными из азотистых
оснований. Поскольку обход вершин этих крестов должен совершаться
в противоположных направлениях, то для совмещения спиральности, кресты
необходимо развернуть так, чтобы направление их винтового
вращения
совпали.
рис. 3
Фундаментальность этих тождество
означает, что отныне теория электромагнитного поля может быть применима не
только к физике, а вообще к любой сфере научной и общественной деятельности.
2. РУССКАЯ МАТРИЦА
ГЕНЕТИЧЕСКОГО КОДА
Существуют всего четыре
(!!) типа
азотистых оснований: аденин
и гуанин
(азотистые основания пуринового ряда), тимин
и цитозин
(основания пиримидинового ряда). Их сокращенно обозначают по
начальным буквам: А, Г, Т, Ц.
Каждая горизонтальная «перекладина»
содержит либо аденин и тимин (А-Т
или Т-А), либо
гуанин и цитозин (Г-Ц
или Ц-Г).
Соединения аденина с гуанином (А-Г),
а также тимина с цитозином (Т-Ц)
не реализуются.
Считается,
что определенное чередование пар
А- Т,
Т-А,
Г-Ц
и
Ц-Г
вдоль «лестницы» и есть генетический код,
фиксирующий индивидуальность данного живого организма. Несмотря на то что
используются только четыре типа «перекладин», огромное количество этих
«перекладин» на «лестнице» позволяет записать в молекуле ДНК всю наследственную
информацию.
Двойная спираль ДНК позволяет высказать предположение о том, что эти спирали
формируются двумя животворящими крестами, составленными из азотистых
оснований. Поскольку обход вершин этих крестов должен совершаться
в противоположных направлениях, то для совмещения спиральности, кресты
необходимо развернуть так, чтобы направление их винтового
вращения
совпали.
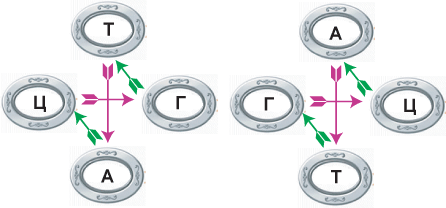 рис.4
Рисунок 4, в первом
приближении, обосновывает причину появления такой избирательности азотистых
оснований. Приведенные выше комбинации азотистых оснований закручиваются в
двойную спираль.
Рисунок иллюстрирует замечательное свойство
спиралей ДНК. Они оказываются фактически закручены в одну и ту же сторону (правоспиральность).
Отметим, что в
латинском алфавите используются следующие обозначения:
А=А; Ц=С; Г=G;
У=U.
В этой цепочке Тимин замещен сходным по
свойствам Урацилом.
В
результате мы можем "Замысел Творения" генетического кода
("базисный генотип") записать в следующей форме
рис.4
Рисунок 4, в первом
приближении, обосновывает причину появления такой избирательности азотистых
оснований. Приведенные выше комбинации азотистых оснований закручиваются в
двойную спираль.
Рисунок иллюстрирует замечательное свойство
спиралей ДНК. Они оказываются фактически закручены в одну и ту же сторону (правоспиральность).
Отметим, что в
латинском алфавите используются следующие обозначения:
А=А; Ц=С; Г=G;
У=U.
В этой цепочке Тимин замещен сходным по
свойствам Урацилом.
В
результате мы можем "Замысел Творения" генетического кода
("базисный генотип") записать в следующей форме
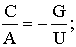 Рассмотрим, как это тождество порождает
двойные спирали ДНК.
Рассмотрим, как это тождество порождает
двойные спирали ДНК.
 рис. 5
Из данного рисунка видны сокровенные тайны формирования матрицы генетического
кода.
Во-первых, четыре кодона любого базисного генотипа,
на любом уровне иерархии, отражают равновесность взаимоотношений:
значение каждого кодона определяется через три других (триединство).
Во-вторых, матрица имеет четко выделенные
четыре сектора, т.е. каждый уровень иерархии двойной спирали ДНК формируется по
образу и подобию.
В-третьих,
главные диагонали матрицы формируются, по образу и подобию, цепочками кодонов
вида
рис. 5
Из данного рисунка видны сокровенные тайны формирования матрицы генетического
кода.
Во-первых, четыре кодона любого базисного генотипа,
на любом уровне иерархии, отражают равновесность взаимоотношений:
значение каждого кодона определяется через три других (триединство).
Во-вторых, матрица имеет четко выделенные
четыре сектора, т.е. каждый уровень иерархии двойной спирали ДНК формируется по
образу и подобию.
В-третьих,
главные диагонали матрицы формируются, по образу и подобию, цепочками кодонов
вида
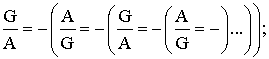 При
этом каждая главная диагональ представляет собой, в свою очередь, двойную
цепочку вида
При
этом каждая главная диагональ представляет собой, в свою очередь, двойную
цепочку вида
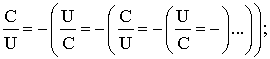 В-четвертых,
каждая диагональ представляет собой такую последовательность "базисных
генотипов", в которой один кодон принадлежит одновременно двум
смежным "базисным генотипам".
В-пятых,
с увеличением уровня иерархии "базисного кодона", его структура не изменяется,
увеличивается только сложность внутренней структуры "базисных генотипов".
В-шестых,
данный
метод формирования двойной спирали ДНК, по образу и подобию, порождает
Русскую матрицу генетического кода.
В-четвертых,
каждая диагональ представляет собой такую последовательность "базисных
генотипов", в которой один кодон принадлежит одновременно двум
смежным "базисным генотипам".
В-пятых,
с увеличением уровня иерархии "базисного кодона", его структура не изменяется,
увеличивается только сложность внутренней структуры "базисных генотипов".
В-шестых,
данный
метод формирования двойной спирали ДНК, по образу и подобию, порождает
Русскую матрицу генетического кода.
 рис. 6
В этой матрице любой кодон оказывается смежным трем другим кодонам, порождая
таким образом собственную самодостаточность (2/3).
3. РУССКАЯ МАТРИЦА
И БИНОМ НЬЮТОНА
рис. 6
В этой матрице любой кодон оказывается смежным трем другим кодонам, порождая
таким образом собственную самодостаточность (2/3).
3. РУССКАЯ МАТРИЦА
И БИНОМ НЬЮТОНА
Правила
задания структурной сложности между элементами иерархических систем и подсистем
могут быть заданы методами перебора различных возможных значений, т. е. числом
сочетаний из m
элементов по n, которое обозначается через
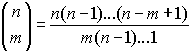 (*)
(*)
Величину называют биномиальными
коэффициентами. называют биномиальными
коэффициентами.
Соотношения (*) можно использовать для определения биномиальных коэффициентов даже в том
случае, если n не является целым
числом (но для целых m). В качестве частных случаев справедливы
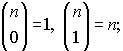
Существуют буквально тысячи тождеств, включающих в себя
биномиальные коэффициенты. Таких соотношений настолько много, что каждое новое
тождество уже никого не волнует, разве что самого автора. Все это говорит об их
чрезвычайно широкой области применения. Из всех свойств биномиальных
коэффициентов наиболее важное значение имеет биномиальная теорема
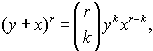
где k=0,r,
где r - целое число.
В соотношении (4)
на индекс к не наложено никаких ограничений, т. к. при к<r соответствующие члены
равны нулю. Биномиальная теорема утверждает, что данное соотношение справедливо
для всех r, если
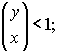
Частный случай, когда у=1 имеет
большое значение, поэтому отметим его специально
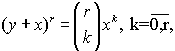
Полагая r =0,1,2, ...
мы получим последовательность биномиальных рядов, которая носит специальное
название–треугольник Паскаля. Наиболее важное свойство биномиальных
коэффициентов заключается в их удивительной симметричности.
Запишем треугольник Паскаля в виде
следующей числовой
матрицы.
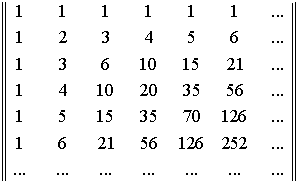
Складывая
коэффициенты этих симметричных рядов, мы получим свертку арифметического ряда
1,2,4,8,16,32,....
Этот
ряд в Русской матрице называют биоспиралью (Русская
матрица).
Фундаментальный характер биномиальных
коэффициентов, их повсеместное применение в различных разделах математики и
других приложениях ни у кого не вызывает сомнения. Можно уверенно сказать, что
между биномом Ньютона (и биномиальными коэффициентами) и законами симметрии
существует тесная связь, что бином Ньютона и биномиальные коэффициенты
отражают в себе самые фундаментальные свойства Единого закона -механизм
функционирования этого закона.
Взаимосвязь между
биномиальными коэффициентами, из которых формируется арифметический ряд
можно отобразить в следующем виде.
 рис.
7
Перепишем приведенные выше формулы в виде следующего тождества.
рис.
7
Перепишем приведенные выше формулы в виде следующего тождества.
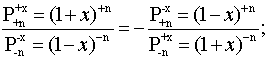 Эти весы отражают взаимодополнительность производящих
функций арифметических рядов.
Но эти ряды обладают уникальными
свойствами.
Рассмотрим взаимосвязь следующих производящих функций
Эти весы отражают взаимодополнительность производящих
функций арифметических рядов.
Но эти ряды обладают уникальными
свойствами.
Рассмотрим взаимосвязь следующих производящих функций
P0(x)=1;
P1(x)=(1-x)-1=1-x+x2-x3+
...
P2(x)=(1-x)-2=1-2x+3x2-4x3+...
P3(x)=(1-x)-3=1-3x+6x2-10x3+...
P4(x)=(1-x)-4=1-5x+14x2-30x3+...
Применяя к
n-мерной производящей функции
Pi(x),
i=1,2,3,...оператор
G(x)=(1-х)+1,
мы получим следующие производящие функции
G(x)=1+х;
G1(x)=1-2x+2x2-2x3+
...
G2(x)=1-3x+5x2-7x3+
...
G3(x)=1-4x+
9x2-16x3+
...
G4(х)=1-5х+14х2-30х3+...
....
 рис.
8
Увязывая производящие функции
Pn(x)
и Gn(х)
в единую схему, мы
получим
рис.
8
Увязывая производящие функции
Pn(x)
и Gn(х)
в единую схему, мы
получим
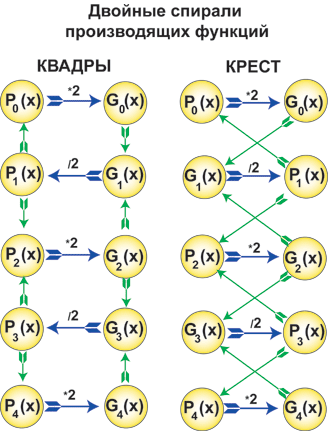 рис.
9
На
странице "Эволюция размерности" были приведены свойства
Русской матрицы, порождающей систему размерностей физических величин. При этом
взаимосвязь между Пространством (Т) и Временем (L)
(между размерностями физических величин) была отражена через
операторы дифференцирования.
рис.
9
На
странице "Эволюция размерности" были приведены свойства
Русской матрицы, порождающей систему размерностей физических величин. При этом
взаимосвязь между Пространством (Т) и Временем (L)
(между размерностями физических величин) была отражена через
операторы дифференцирования.
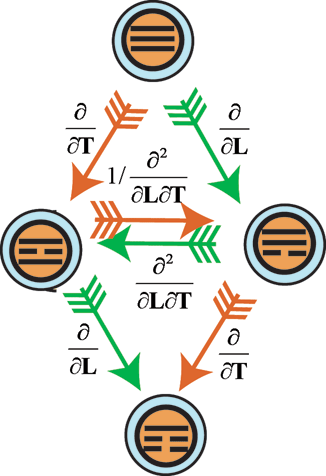
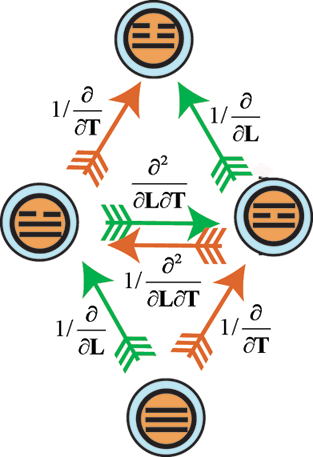 рис. 10-1
рис. 10-2
Общая
схема эволюции физических размерностей была рассмотрена на схеме
рис. 10-1
рис. 10-2
Общая
схема эволюции физических размерностей была рассмотрена на схеме
 рис. 11
Из
этой схемы был сделан вывод, что частное дифференцирование собственных
пространств и подпространств системы "Пространство-Время" порождает
арифметический ряд
рис. 11
Из
этой схемы был сделан вывод, что частное дифференцирование собственных
пространств и подпространств системы "Пространство-Время" порождает
арифметический ряд
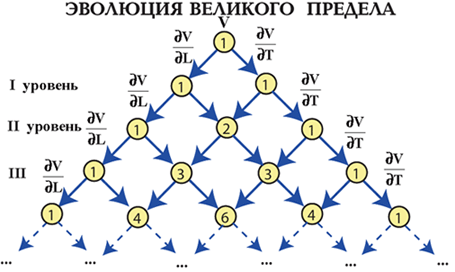 рис. 12
Теперь можно привести общую схему,
отражающую взаимосвязь между Русской матрицей и биномом Ньютона
рис. 12
Теперь можно привести общую схему,
отражающую взаимосвязь между Русской матрицей и биномом Ньютона
 рис. 13
Этот рисунок является гимном законам сохранения симметрии. Он
органически синтезировал в себе
гармонию Русской матрицы, гармонию цветов радуги и
музыкальных гамм, гармонию двойных спиралей генетического кода, гармонию
двойных спиралей Периодической системы химических элементов, гармонию
микромира, макромира и мегамира.
Более подробно о свойствах Русской матрицы, жизнеутверждающей концепцию
Пифагора "Все есть Число", можно получить на многих других страницах моего
сайта.
Здесь отметим только еще одно свойство
Биномиальной Русской матрицы.
рис. 13
Этот рисунок является гимном законам сохранения симметрии. Он
органически синтезировал в себе
гармонию Русской матрицы, гармонию цветов радуги и
музыкальных гамм, гармонию двойных спиралей генетического кода, гармонию
двойных спиралей Периодической системы химических элементов, гармонию
микромира, макромира и мегамира.
Более подробно о свойствах Русской матрицы, жизнеутверждающей концепцию
Пифагора "Все есть Число", можно получить на многих других страницах моего
сайта.
Здесь отметим только еще одно свойство
Биномиальной Русской матрицы.
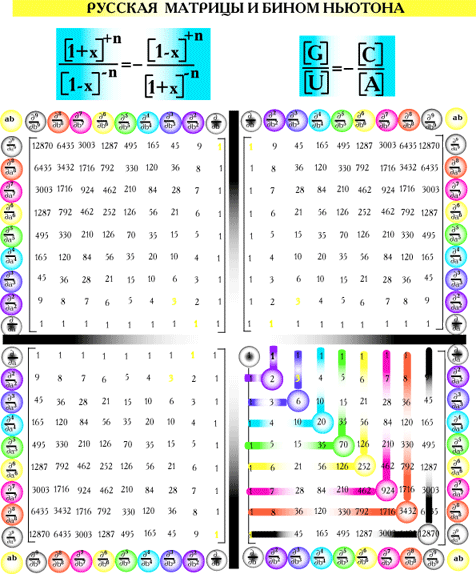 рис. 14
Строки и столбцы каждого из четырех
секторов этой Русской матрицы формируют коэффициенты производящих
бесконечномерных рядов вида
рис. 14
Строки и столбцы каждого из четырех
секторов этой Русской матрицы формируют коэффициенты производящих
бесконечномерных рядов вида
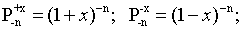 В то время как фрагменты строки и
столбца, имеющие общий элемент, стоящий на главной диагонали
формируется конечными производящими
рядами вида
В то время как фрагменты строки и
столбца, имеющие общий элемент, стоящий на главной диагонали
формируется конечными производящими
рядами вида
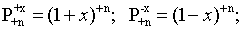 4.
ПЛАН СЧЕТОВ ЗАКОНОВ СОХРАНЕНИЯ СИММЕТРИИ
Поскольку
законы сохранения симметрии никогда не нарушаются, т.к. одна
форма симметрии всегда трансформируется в другую,
то, следовательно, в
Мироздании существуют природные операционные механизмы, которые ведут
строгий бухгалтерский счет и учет, что каждое мироздание имеет собственный
"План счетов".
Актив или Пассив?
Дебит или Кредит?
Эти слова и их смыслы хорошо известны
экономистам и бухгалтерам. Их смысл состоит в том, что
"Нельзя потратить больше, чем имеешь в целом!"
Эта прописная бухгалтерская
истина отражается в главном бухгалтерском документе - бухгалтерском
балансе предприятия, имеющего два взаимодополнительных раздела -
Актив (размещенные
средства) и Пассив
(источники средств).
Это важнейшая перекладина весов
бухгалтерского баланса будет справедлива и для Плана счетов законов
сохранения симметрии
4.
ПЛАН СЧЕТОВ ЗАКОНОВ СОХРАНЕНИЯ СИММЕТРИИ
Поскольку
законы сохранения симметрии никогда не нарушаются, т.к. одна
форма симметрии всегда трансформируется в другую,
то, следовательно, в
Мироздании существуют природные операционные механизмы, которые ведут
строгий бухгалтерский счет и учет, что каждое мироздание имеет собственный
"План счетов".
Актив или Пассив?
Дебит или Кредит?
Эти слова и их смыслы хорошо известны
экономистам и бухгалтерам. Их смысл состоит в том, что
"Нельзя потратить больше, чем имеешь в целом!"
Эта прописная бухгалтерская
истина отражается в главном бухгалтерском документе - бухгалтерском
балансе предприятия, имеющего два взаимодополнительных раздела -
Актив (размещенные
средства) и Пассив
(источники средств).
Это важнейшая перекладина весов
бухгалтерского баланса будет справедлива и для Плана счетов законов
сохранения симметрии
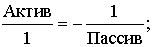 Эти весы отражают равновесность (баланс) между суммой Актива и суммой
Пассива.
Эти бухгалтерские весы отражают
равновесность экономических систем (микроэкономики, макроэкономики, мировой
экономики).
Если правая
(левая) часть тождества начинает увеличиваться, то соответственно левая
(правая) часть тождества начинает уменьшается.
Это тождество характеризует закон
сохранения:
"Что от одного "тела" -Актива (или Пассива) убудет, то присовокупится к
другому -Пассиву (или Активу).
Закон симметрии (баланса) между
Активом и Пассивом в системе бухгалтерского учета проявляется через
категории бухгалтерского счета ("Дебит" и "Кредит"), взаимоотношения между
которыми описывается аналогичным тождеством
Эти весы отражают равновесность (баланс) между суммой Актива и суммой
Пассива.
Эти бухгалтерские весы отражают
равновесность экономических систем (микроэкономики, макроэкономики, мировой
экономики).
Если правая
(левая) часть тождества начинает увеличиваться, то соответственно левая
(правая) часть тождества начинает уменьшается.
Это тождество характеризует закон
сохранения:
"Что от одного "тела" -Актива (или Пассива) убудет, то присовокупится к
другому -Пассиву (или Активу).
Закон симметрии (баланса) между
Активом и Пассивом в системе бухгалтерского учета проявляется через
категории бухгалтерского счета ("Дебит" и "Кредит"), взаимоотношения между
которыми описывается аналогичным тождеством
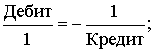 Это тождество является базисным бухгалтерским счетом, из которого
раскручивается двойная спираль бухгалтерских счетов. Свертка остатков
бухгалтерских счетов в итоговый счет порождает заключительную строку любого
бухгалтерского баланса.
По этой причине все счета, относящиеся к Активу, носят название
Активные счета, в то
время как все счета, расположенные в разделе Пассива, носят название
Пассивные счета.
Если определить
оборот как сумму расходов за расчетный период, то мы можем определить Сальдо
конечное для Активных и Пассивных счетов
Для Активных счетов формула для Сальдо
конечного будет иметь вид
Сальдо конечное =Сальдо начальное + оборот по Дебиту - оборот по Кредиту
Для Пассивных счетов Сальдо конечное будет
считаться уже по иному
Сальдо конечное =Сальдо начальное + оборот по Кредиту - оборот по Дебиту
Таким
образом, правила двойного счета, которые проявляются в
бухгалтерских проводках, гласят:
"Если мы записали определенную сумму в дебит одного счета,
то мы должны записать эту же сумму в кредит другого счета".
Нетрудно осознать, что система бухгалтерского учета отражает в себе
природные операционные механизмы Единого закона эволюции двойственного
отношения "Актив-Пассив", которое на начало очередного расчетного периода
представляется как Сальдо начальное, равное Сальдо конечное предыдущего
расчетного периода.
При этом природные операционные механизмы Единого закона эволюции
двойственного отношения "Дебит-Кредит" формируют "четыре базисные стихии"
Плана счетов
Это тождество является базисным бухгалтерским счетом, из которого
раскручивается двойная спираль бухгалтерских счетов. Свертка остатков
бухгалтерских счетов в итоговый счет порождает заключительную строку любого
бухгалтерского баланса.
По этой причине все счета, относящиеся к Активу, носят название
Активные счета, в то
время как все счета, расположенные в разделе Пассива, носят название
Пассивные счета.
Если определить
оборот как сумму расходов за расчетный период, то мы можем определить Сальдо
конечное для Активных и Пассивных счетов
Для Активных счетов формула для Сальдо
конечного будет иметь вид
Сальдо конечное =Сальдо начальное + оборот по Дебиту - оборот по Кредиту
Для Пассивных счетов Сальдо конечное будет
считаться уже по иному
Сальдо конечное =Сальдо начальное + оборот по Кредиту - оборот по Дебиту
Таким
образом, правила двойного счета, которые проявляются в
бухгалтерских проводках, гласят:
"Если мы записали определенную сумму в дебит одного счета,
то мы должны записать эту же сумму в кредит другого счета".
Нетрудно осознать, что система бухгалтерского учета отражает в себе
природные операционные механизмы Единого закона эволюции двойственного
отношения "Актив-Пассив", которое на начало очередного расчетного периода
представляется как Сальдо начальное, равное Сальдо конечное предыдущего
расчетного периода.
При этом природные операционные механизмы Единого закона эволюции
двойственного отношения "Дебит-Кредит" формируют "четыре базисные стихии"
Плана счетов
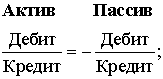 Это тождество характеризует законы сохранения симметрии Сальдо Активных и
Пассивных счетов, т.е. в бухгалтерских проводках, при определенных
ситуациях, счета Актива и Пассива будут являться взаимодополнительными.
Бухгалтера хорошо знают эти свойства Плана счетов, когда активные счета
проявляют свойства пассивных счетов и наоборот, пассивные счета ведут себя
как активные.
Законы сохранения симметрии, отражаемые в бухгалтерском учете, в полной мере
отражаются в микроэкономике, макроэкономике и мировой экономике.
Эта двойная
бухгалтерия проявляется при анализе любой экономической монады:
"товар-деньги", "спрос-предложение",
"безработица-занятость", "инфляция-дефляция", "объект хозяйствования -
субъект хозяйствования", и т.д.
Эта
двойная бухгалтерия проявляется не только во всех сферах экономики
(микроэкономике, макроэкономике, мировой экономике), но и вообще во всех
сферах жизнедеятельности современной цивилизации.
И сейчас мы убеждаемся, что Русская матрица построена в точном соответствии
с системой бухгалтерских счетов.
Это тождество характеризует законы сохранения симметрии Сальдо Активных и
Пассивных счетов, т.е. в бухгалтерских проводках, при определенных
ситуациях, счета Актива и Пассива будут являться взаимодополнительными.
Бухгалтера хорошо знают эти свойства Плана счетов, когда активные счета
проявляют свойства пассивных счетов и наоборот, пассивные счета ведут себя
как активные.
Законы сохранения симметрии, отражаемые в бухгалтерском учете, в полной мере
отражаются в микроэкономике, макроэкономике и мировой экономике.
Эта двойная
бухгалтерия проявляется при анализе любой экономической монады:
"товар-деньги", "спрос-предложение",
"безработица-занятость", "инфляция-дефляция", "объект хозяйствования -
субъект хозяйствования", и т.д.
Эта
двойная бухгалтерия проявляется не только во всех сферах экономики
(микроэкономике, макроэкономике, мировой экономике), но и вообще во всех
сферах жизнедеятельности современной цивилизации.
И сейчас мы убеждаемся, что Русская матрица построена в точном соответствии
с системой бухгалтерских счетов.
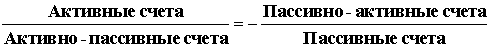 Может быть теперь ученые всех направлений, включая руководителей всех
уровней смогут, наконец, осмыслить сущность "бухгалтерских
проводок", которые они формировать в процессе своей практической и
теоретической деятельности. И, в первую очередь, эти "бухгалтерские
проводки" должны освоить политические и общественные деятели.
Может быть, настала пора любую "стратегическую инициативу", сначала
пропустить через "План счетов" законов симметрии, что любому решению всегда
соответствует взаимодополнительное решение, и если "кажущееся добро"
какой-либо "бухгалтерской проводки" оборачивается реальным злом для
общества, то такие деятели должны немедленно освобождаться от занимаемых
должностей. И неважно, по какой причине они совершили ошибки (по умыслу ли,
по недомыслию ли).
"План счетов" Русской матрицы позволяет осознать правоту концепции
Пифагора:
"Все есть Число". Каждое число Русской матрицы является золотой константой,
которая, по образу и подобию. может порождать собственное мироздание Русских
матриц, разворачивая соответствующие "бухгалтерские проводки", а может и
сворачиваться в единственное золотое число, которое отражает "бухгалтерский
баланс" жизнедеятельности "мироздания".
Может быть теперь ученые всех направлений, включая руководителей всех
уровней смогут, наконец, осмыслить сущность "бухгалтерских
проводок", которые они формировать в процессе своей практической и
теоретической деятельности. И, в первую очередь, эти "бухгалтерские
проводки" должны освоить политические и общественные деятели.
Может быть, настала пора любую "стратегическую инициативу", сначала
пропустить через "План счетов" законов симметрии, что любому решению всегда
соответствует взаимодополнительное решение, и если "кажущееся добро"
какой-либо "бухгалтерской проводки" оборачивается реальным злом для
общества, то такие деятели должны немедленно освобождаться от занимаемых
должностей. И неважно, по какой причине они совершили ошибки (по умыслу ли,
по недомыслию ли).
"План счетов" Русской матрицы позволяет осознать правоту концепции
Пифагора:
"Все есть Число". Каждое число Русской матрицы является золотой константой,
которая, по образу и подобию. может порождать собственное мироздание Русских
матриц, разворачивая соответствующие "бухгалтерские проводки", а может и
сворачиваться в единственное золотое число, которое отражает "бухгалтерский
баланс" жизнедеятельности "мироздания".
|

 "Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
"Каждая
цивилизация в определенном возрасте имеет возможность возвысить, или
разрушить себя. Если делается выбор в пользу возвышения, то возникает
импульс, позволяющий появиться учениям об утерянных законах сущего". (Высший
разум, ченнелинг).
М.И. Беляев, 2015г,©
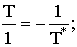

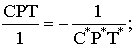
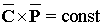
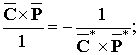
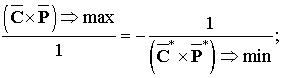
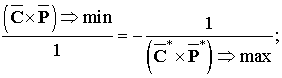
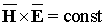
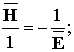



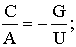

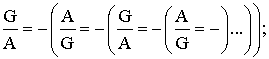
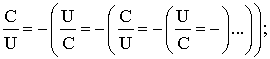

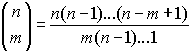 (
(