треугольник

1. Точки и линии, связанные с треугольником [ ред. | ред. код ]
2. Вычисление площади треугольника [ ред. | ред. код ]
3. С использованием векторов [ ред. | ред. код ]
4. Тригонометрический способ [ ред. | ред. код ]
5. Использование координат [ ред. | ред. код ]
6. Формула Герона [ ред. | ред. код ]
7. Формулы, похожие на формулу Герона [ ред. | ред. код ]
8. Используя Теорема Пика [ ред. | ред. код ]
9. Другие формулы вычисления площади [ ред. | ред. код ]
10. Вычисления площади прямоугольного треугольника [ ред. | ред. код ]
11. Вычисления сторон и углов [ ред. | ред. код ]
12. Тригонометрические отношения в прямоугольных треугольниках [ ред. | ред. код ]
13. Синус, косинус и тангенс [ ред. | ред. код ]
14. Обратные функции [ ред. | ред. код ]
15. Теоремы синусов, косинусов и тангенсов [ ред. | ред. код ]
16. Еще формулы для треугольников Евклидовой геометрии [ ред. | ред. код ]
17. Неплощинни треугольники [ ред. | ред. код ]

треугольник в евклидовой геометрии - геометрическая фигура , Которая состоит из трех точек , Не лежащие на одной прямой И трех отрезков , Которые соединяют. Треугольник с вершинами A, B, и C сказывается ABC. треугольник является многоугольником и 2 симплексов . В евклидовой геометрии треугольник однозначно задает плоскость . Все треугольники двумерные.

Основные сведения о треугольники были приведены Евклидом в его работе «Элементы» рядом с 300 до н. е.

Треугольники можно классифицировать в зависимости от взаимных длин его сторон:

• Равносторонним называется треугольник, у которого все стороны имеют одинаковую длину. Все углы равностороннего треугольника также равны и равны 60 °, а центры вписанного и описанного кругов совпадают. Равносторонний треугольник еще называют правильным .
• Равнобедренным называется треугольник, у которого две стороны имеют одинаковую длину. Эти стороны называются боковыми, третья сторона при этом называется основой треугольника. В равнобедренном треугольнике углы при его основании равны.
• Разносторонним называется треугольник, у которого все стороны имеют разную длину. Внутренние углы разностороннего треугольника разные.

• равносторонний

• равнобедренный

• разносторонний

Также треугольники можно классифицировать в соответствии с их внутренних углов:

• Если один из внутренних углов равен 90 ° ( прямой угол ), То треугольник называется прямоугольным . Сторона, противоположная прямого угла, называется гипотенузой , А другие две стороны - катетами .
• Если один из внутренних углов больше 90 °, то треугольник называется тупоугольный .
• Если все углы треугольника меньше 90 °, то треугольник называется остроугольным. Равносторонний треугольник является остроугольным, но не все остроугольные треугольники равносторонние.

Точки и линии, связанные с треугольником [ ред. | ред. код ]

Есть сотни различных построений для определения особых точек внутри треугольника, которые удовлетворяют некоторые уникальные условия (см в списке ссылок перечень статей). Часто необходимо построить три прямые, связанные аналогично с тремя сторонами (вершинами, углами) треугольника и тогда убедиться, что они пересекаются в одной точке. Важным инструментом для проверки этого является теорема Чеви , Которая дает критерии для определения конкурентности прямых . Подобно этому, линии связанные с треугольником часто строятся после проверки, три аналогичным образом полученные точки есть коллинеарны - теорема Менелая дает для этого случая общий критерий. В этом разделе приведены только такие построения, наиболее часто встречаются.

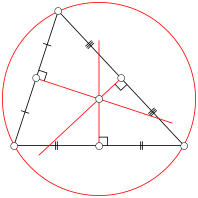
Центр описанной окружности.

срединный перпендикуляр треугольника - это перпендикуляр , Который проходит посередине стороны треугольника. Три срединные перпендикуляры пересекаются в одной точке, которая является центром описанной окружности . Диаметр описанной окружности можно определить с теоремы синусов .

исходя из теоремы Фалеса , Можно утверждать, если центр описанной окружности расположен на одной из сторон треугольника, тогда противоположный угол прямой. Более того, если центр описанной окружности находится внутри треугольника, то треугольник остроугольный, а если наружу, то треугольник тупоугольный.

Высота треугольника - прямая проведена с вершины и перпендикулярна к противоположной стороне или к продолжению противоположной стороны. Эта сторона называется основанием треугольника. Точка пересечения стороны и перпендикуляра называется основой перпендикуляра. Длина высоты - это расстояние от вершины к основанию треугольника. Три высоты пересекаются в одной точке, которая называется ортоцентром треугольника. ортоцентр лежит внутри треугольника (и соответственно все основания перпендикуляров лежат в треугольнике) тогда и только тогда, когда треугольник НЕ тупоугольный (в нем ни один из внутренних углов больше прямой угол). смотрите также ортоцентрична система

биссектриса треугольника - это прямая проведена через вершину, которая делит соответствующий угол на две равные части. Три биссектрисы пересекаются в одной точке, инцентри , центре вписанного в треугольник окружности. Вписана окружность - это круг, который лежит внутри треугольника и примыкает к трем его сторон. Кроме того, есть еще три важных круга, внешние вписаны; они лежат за пределами треугольника и соприкасаются с одной его стороны, а также к продолжению других двух. Центры внутреннего и внешних вписанных кругов образуют ортоцентричну систему .

медиана треугольника - это прямая проведена через вершину и середину противоположной стороны и делит треугольник на два одинаковой площади. Три медианы пересекаются в одной точке, которая называется центроидом треугольника. Эта точка также центр масс треугольника: если бы треугольник был сделан из дерева, то можно было бы держать равновесие держа за центроид. Центроид делит каждую медиану в соотношении 2: 1, например расстояние между вершиной и центроидом вдвое больше, чем между центроидом и противоположной стороной.

Окружность девяти точек.

Средние точки трех сторон и основы трех высот все лежат на одном круге, которое называется кругом девяти точек треугольника. Остальные три точки, через которые круг получило свое название, это середины той части высоты, лежащий между ортоцентром и вершиной. Радиус окружности девяти точек равна половине описанной окружности . Оно соприкасается с вписанной окружности (в точке Фейербаха ) И до трех внешних вписанных кругов.

Центроид (желтый), ортоцентр (синий), центр описанной окружности (зеленый) и центр окружности девяти точек (красная точка) все лежат на одной линии, которая называется линия Эйлера (Красная линия). Центр окружности девяти точек лежит на середине между ортоцентром и центром описанной окружности, а расстояние между центроидом и центром описанной окружности равен половине расстояния между центроидом и ортоцентром.

Вершины треугольника обычно обозначают большими латинскими буквами A, B, C, углы при соответствующих вершинах греческими буквами α, β, γ, а длины противоположных сторон - маленькими латинскими буквами a, b, c.

Сумма внутренних углов треугольника - 180 градусов. Внешний угол треугольника ( угол смежный к внутреннему углу) всегда равна сумме двух других внутренних углов треугольника. Как и во всех выпуклых многогранников сумма внешних углов треугольника 360 градусов.

α + β + γ = 180 ∘ {\ displaystyle \ alpha + \ beta + \ gamma \ = 180 ^ {\ circ}}

Сумма длин двух любых сторон треугольника всегда превышает длину третьей стороны. это неравенство треугольника или аксиома треугольника (в частном случае равенства два угла уменьшаются до нуля и треугольник вырождается в отрезок).

Два треугольника называются подобными тогда и только тогда, если углы одного уровне соответствующим углам другого. В таком случае длины соответствующих сторон пропорциональны . Так может быть например, когда в двух треугольников есть общий угол, а стороны противоположные этом углу - параллельны. Вот несколько постулатов и теорем о подобных треугольника:

• Два треугольника подобны, если в них хотя бы два соответствующих угла уровне.
• Если две соответствующие стороны в треугольниках пропорциональны, а угол между ними одинаковый, то треугольники подобны.
• Если все стороны двух треугольников пропорциональны, то треугольники подобны.

Два треугольника называются конгруэнтными , Если все их соответствующие стороны и углы равны (6 элементов). Несколько главных постулатов и теорем о конгруэнтные треугольники:

• Постулат SAS (side-angle-side) Если две стороны и угол между ними в треугольников соответственно равны, то треугольники конгруэнтны.
• Постулат SSS: Если все соответствующие стороны в треугольников равны, то треугольники конгруэнтны.
• Постулат ASA Если сторона и прилегающие к ней углы в треугольников соответственно равны, то треугольники конгруэнтны.
• Постулат AAS Если два угла и любая сторона в треугольников соответственно равны, то треугольники конгруэнтны.
• Теорема Гипотенуза-катет Если гипотенуза и один катет в прямоугольных треугольников соответственно равны, то треугольники конгруэнтны.

Вычисление площади треугольника [ ред. | ред. код ]

Вычисление площади треугольника является простой задачей, которая часто решается во многих отраслях. Самая известная и самая формула:

S = 1 2 b h {\ displaystyle S = {\ frac {1} {2}} bh}

где S - площадь, b - длина основания треугольника а h - высота треугольника, относительная к основанию. Хотя эта формула и простая, она может быть использована только, если можно легко найти высоту. Например, землемер участка треугольной формы измеряет длину каждой стороны и может найти площадь без определения длины высоты. На практике можно использовать различные методы определения площади, в зависимости от того, что известно о треугольнике. Ниже приведены подборку применяемым формул.

С использованием векторов [ ред. | ред. код ]

площадь параллелограмма можно вычислить с помощью векторов . Пусть векторы AB и AC направлены соответственно от A до B и от A до C. Тогда площадь параллелограмма ABDC равна | AB × AC | , То есть числовое значение векторного произведения AB и AC. | AB × AC | равна | h × AC | , Где h - высота параллелограмма как вектор.

Площадь треугольника ABC равна половине площади параллелограмма S = ½ | AB × AC | .

Площадь треугольника ABC можно вычислить как скалярное произведение векторов.

1 февраля (A B ⋅ A B) (A C ⋅ A C) - (A B ⋅ A C) 2 = 1 | 2 | A B | 2 | A C | 2 - (A B ⋅ A C) 2. {\ Displaystyle {\ frac {1} {2}} {\ sqrt {(\ mathbf {AB} \ cdot \ mathbf {AB}) (\ mathbf {AC} \ cdot \ mathbf {AC}) - (\ mathbf { AB} \ cdot \ mathbf {AC}) ^ {2}}} = {\ frac {1} {2}} {\ sqrt {| \ mathbf {AB} | ^ {2} | \ mathbf {AC} | ^ {2} - (\ mathbf {AB} \ cdot \ mathbf {AC}) ^ {2}}} \ ,.}

Тригонометрический способ вычисления высоты h.

Тригонометрический способ [ ред. | ред. код ]

Высоту треугольника можно определить используя тригонометрические формулы. Согласно обозначением, как на рисунке слева, высота равна h = a sin γ. Подставив высоту в формулу S = ½bh, приведенной выше, получим:

S = 2 января a b sin ⁡ γ = 2 января b c sin ⁡ α = 2 января c a sin ⁡ β. {\ Displaystyle S = {\ frac {1} {2}} ab \ sin \ gamma = {\ frac {1} {2}} bc \ sin \ alpha = {\ frac {1} {2}} ca \ sin \ beta.}

Кроме того, sin α = sin (π - α) = sin (β + γ), что справедливо и для других двух углов:

S = 1 февраля a b sin ⁡ (α + β) = 1 февраля b c sin ⁡ (β + γ) = 1 февраля c a sin ⁡ (γ + α). {\ Displaystyle S = {\ frac {1} {2}} ab \ sin (\ alpha + \ beta) = {\ frac {1} {2}} bc \ sin (\ beta + \ gamma) = {\ frac {1} {2}} ca \ sin (\ gamma + \ alpha).}

Зная сторону и два угла, один из которых прилегающий:

S = b 2 (sin ⁡ α) (sin ⁡ (α + β)) 2 sin ⁡ β, {\ displaystyle S = {\ frac {b ^ {2} (\ sin \ alpha) (\ sin (\ alpha + \ beta))} {2 \ sin \ beta}}}

и аналогично если известны стороны a или c.

Зная сторону и два прилегающие углы: [1]

S = a 2 2 (cot ⁡ β + cot ⁡ γ) = a 2 (sin ⁡ β) (sin ⁡ γ) 2 sin ⁡ (β + γ), {\ displaystyle S = {\ frac {a ^ {2} } {2 (\ cot \ beta + \ cot \ gamma)}} = {\ frac {a ^ {2} (\ sin \ beta) (\ sin \ gamma)} {2 \ sin (\ beta + \ gamma) }}}

и аналогично если известны стороны b или c.

Использование координат [ ред. | ред. код ]

Если точка А находится в точке отсчета (0, 0) Декартовой координатной системы , А координаты двух других точек B = (x B, y B) и C = (x C, y C), тогда площадь S может быть вычислена как ½ абсолютного значения детерминанту :

S = 1 | 2 | det (x B x C y B y C) | = 1 | 2 | x B y C - x C y B | . {\ Displaystyle S = {\ frac {1} {2}} \ left | \ det {\ begin {pmatrix} x_ {B} & x_ {C} \\ y_ {B} & y_ {C} \ end {pmatrix}} \ right | = {\ frac {1} {2}} | x_ {B} y_ {C} -x_ {C} y_ {B} |.}

В общем случае:

S = 1 | 2 | det (x A x B x C y A y B y C 1 января 1) | = 1 | 2 | x A y C - x A y B + x B y A - x B y C + x C y B - x C y A | . {\ Displaystyle S = {\ frac {1} {2}} \ left | \ det {\ begin {pmatrix} x_ {A} & x_ {B} & x_ {C} \\ y_ {A} & y_ {B} & y_ { C} \\ 1 & 1 & 1 \ end {pmatrix}} \ right | = {\ frac {1} {2}} {\ big |} x_ {A} y_ {C} -x_ {A} y_ {B} + x_ { B} y_ {A} -x_ {B} y_ {C} + x_ {C} y_ {B} -x_ {C} y_ {A} {\ big |}.}

В трехмерном пространстве площадь треугольника {A = (x A, y A, z A), B = (x B, y B, z B) и C = (x C, y C, z C)} равна пифагорова сумме соответствующих проекций на три главные плоскости (для которых x = 0 или y = 0 или z = 0):

S = 1 2 (det (x A x B x C y A y B y C 1 1 1)) 2 + (det (y A y B y C z A z B z C 1 1 1)) 2 + (det (z A z B z C x A x B x C 1 1 1)) 2. {\ Displaystyle S = {\ frac {1} {2}} {\ sqrt {\ left (\ det {\ begin {pmatrix} x_ {A} & x_ {B} & x_ {C} \\ y_ {A} & y_ { B} & y_ {C} \\ 1 & 1 & 1 \ end {pmatrix}} \ right) ^ {2} + \ left (\ det {\ begin {pmatrix} y_ {A} & y_ {B} & y_ {C} \\ z_ { A} & z_ {B} & z_ {C} \\ 1 & 1 & 1 \ end {pmatrix}} \ right) ^ {2} + \ left (\ det {\ begin {pmatrix} z_ {A} & z_ {B} & z_ {C} \\ x_ {A} & x_ {B} & x_ {C} \\ 1 & 1 & 1 \ end {pmatrix}} \ right) ^ {2}}}.}

Формула Герона [ ред. | ред. код ]

Форма треугольника однозначно определяется тремя сторонами. Соответственно для того, чтобы посчитать площадь, достаточно знать длину сторон. по формуле Герона :

S = p (pa) (pb) (pc) {\ displaystyle S = {\ sqrt {p (pa) (pb) (pc)}}}

где p = (a + b + c) / 2 {\ displaystyle p = (a + b + c) / 2} - полупериметр
Другие способы записи формулы Герона:

S = 1 4 (a 2 + b 2 + c 2) 2 - 2 (a 4 + b 4 + c 4). {\ Displaystyle S = {\ frac {1} {4}} {\ sqrt {(a ^ {2} + b ^ {2} + c ^ {2}) ^ {2} 2 (a ^ {4} + b ^ {4} + c ^ {4})}}.} S = 1 4 2 (a 2 b 2 + a 2 c 2 + b 2 c 2) - (a 4 + b 4 + c 4) {\ displaystyle S = {\ frac {1} {4}} {\ sqrt {2 (a ^ {2} b ^ {2} + a ^ {2} c ^ {2} + b ^ {2} c ^ {2}) - (a ^ {4} + b ^ {4} + c ^ {4})}}} S = 1 4 (a + b - c) (a - b + c) (- a + b + c) (a + b + c). {\ Displaystyle S = {\ frac {1} {4}} {\ sqrt {(a + bc) (a-b + c) (- a + b + c) (a + b + c)}}.}

Формулы, похожие на формулу Герона [ ред. | ред. код ]

Есть три формулы, имеющие похожи на формулу Герона, но записаны через другие величины. Обозначив медианы для сторон a, b, и c соответственно как m a, m b, {\ displaystyle m_ {a}, m_ {b}} и m c {\ displaystyle m_ {c}} , А их пивсуму (m a + m b + m c) / 2 {\ displaystyle (m_ {a} + m_ {b} + m_ {c}) / 2} как σ {\ displaystyle \ sigma} , имеем [2]

S = 3 Апреля σ (σ - m a) (σ - m b) (σ - m c). {\ Displaystyle S = {\ frac {4} {3}} {\ sqrt {\ sigma (\ sigma -m_ {a}) (\ sigma -m_ {b}) (\ sigma -m_ {c})}} .}

Тогда, обозначив высоты на стороны a, b, и c соответственно как h a {\ displaystyle h_ {a}} , H b {\ displaystyle h_ {b}} И h c {\ displaystyle h_ {c}} И познавшею пивсуму величин, обратных к высот, как H = (ha - 1 + hb - 1 + hc - 1) / 2 {\ displaystyle H = (h_ {a} ^ {- 1} + h_ {b} ^ { 1} + h_ {c} ^ {- 1}) / 2} , получим [3]

S - 1 = 4 H (H - h a - 1) (H - h b - 1) (H - h c - 1). {\ Displaystyle \ mathrm {S} ^ {- 1} = 4 {\ sqrt {H (H-h_ {a} ^ {- 1}) (H-h_ {b} ^ {- 1}) (H-h_ {c} ^ {- 1})}}.}

Обозначив пивсуму синусов углов как P = [(sin ⁡ α) + (sin ⁡ β) + (sin ⁡ γ)] / 2 {\ displaystyle P = [(\ sin \ \ \ alpha) + (\ sin \ \ \ beta ) + (\ sin \ \ \ gamma)] / 2} , получим [4]

S = D 2 P (P - sin ⁡ α) (P - sin ⁡ β) (P - sin ⁡ γ) {\ displaystyle S = D ^ {2} {\ sqrt {P (P- \ sin \ alpha) ( P- \ sin \ beta) (P- \ sin \ gamma)}}}

где D - диаметр описанной окружности: D = a sin ⁡ α = b sin ⁡ β = c sin ⁡ γ. {\ Displaystyle D = {\ tfrac {a} {\ sin \ alpha}} = {\ tfrac {b} {\ sin \ beta}} = {\ tfrac {c} {\ sin \ gamma}}.}

Используя Теорема Пика [ ред. | ред. код ]

См. Теорема Пика для объяснений, как найти площадь произвольного целочисленного многоугольника.

Теорема утверждает, что

S = I + 1 2 B - 1 {\ displaystyle \ mathrm {S} = I + {\ frac {1} {2}} B-1}

где i - количество целочисленных точек внутри многоугольника, b - количество целочисленных точек на границе многоугольника.

Другие формулы вычисления площади [ ред. | ред. код ]

Существуют и другие формулы для вычисления площади, например,

S = r ⋅ p, {\ displaystyle S = r \ cdot p}

где r - радиус вписанной окружности, и p = (a + b + c) / 2 - (полупериметр)

S = 1 2 D 2 (sin ⁡ α) (sin ⁡ β) (sin ⁡ γ) {\ displaystyle S = {\ frac {1} {2}} D ^ {2} (\ sin \ alpha) (\ sin \ beta) (\ sin \ gamma)}

Для диаметра описанной окружности D; и [5]

S = tan ⁡ α 4 (b 2 + c 2 - a 2) {\ displaystyle S = {\ frac {\ tan \ alpha} {4}} (b ^ {2} + c ^ {2} -a ^ { 2})}

для угла α ≠ {\ displaystyle \ alpha \ neq} 90 °.

В 1885 году, Бейкер [6] дал подборку из более чем сотни различных формул для вычисления площади треугольника (хотя стоит предупредить читателя, что некоторые из них неправильные). Приводим здесь # 9, # 39a, # 39b, # 42, и # 49:

S = 1 2 [a b c h a h b h c] 1/3, {\ displaystyle S = {\ frac {1} {2}} [abch_ {a} h_ {b} h_ {c}] ^ {1/3}} S = 1 2 a b h a h b, {\ displaystyle S = {\ frac {1} {2}} {\ sqrt {abh_ {a} h_ {b}}}} S = a + b 2 (ha - 1 + hb - 1), {\ displaystyle S = {\ frac {a + b} {2 (h_ {a} ^ {- 1} + h_ {b} ^ {- 1 })}}} S = R h b h c a {\ displaystyle S = {\ frac {Rh_ {b} h_ {c}} {a}}}

Для радиуса описанной окружности R, и

S = h a h b 2 sin ⁡ γ. {\ Displaystyle S = {\ frac {h_ {a} h_ {b}} {2 \ sin \ gamma}}.}

Вычисления площади прямоугольного треугольника [ ред. | ред. код ]

В прямоугольном треугольнике можно взять один из катетов как основу, а другой - как его высоту. Отсюда формула прямоугольного треугольника

S = c c '2 {\ displaystyle S = {\ frac {cc'} {2}}}

где S - площадь, а c и c '- катеты.

Вычисления сторон и углов [ ред. | ред. код ]

В общем, есть различные принятые методы вычисления длин сторон и углов треугольника. Если определенные методы могут быть использованы только в прямоугольном треугольнике, то другие могут оказаться нужными для сложных случаев.

Тригонометрические отношения в прямоугольных треугольниках [ ред. | ред. код ]

В прямоугольных треугольниках тригонометрические соотношения - синус, косинус и тангенс могут использоваться, чтобы найти неизвестные углы или неизвестные длины сторон. Стороны треугольника обозначают так:

• гипотенуза - сторона противоположная прямого угла, или самая длинная сторона в прямоугольном треугольнике, в данном случае h.
• Противоположный катет - сторона противоположная угла, рассматривается.
• Прилегающий катет - та сторона, которая прилегает к углу, что рассматривается и к прямому. В данном случае прилегающий катет b.

Синус, косинус и тангенс [ ред. | ред. код ]

Синус угла - это отношение длины противолежащего катета к длине гипотенузы. В нашем случае

sin ⁡ A = opposite hypotenuse = a h. {\ Displaystyle \ sin A = {\ frac {\ textrm {opposite}} {\ textrm {hypotenuse}}} = {\ frac {a} {h}} \ ,.}

Обратите внимание, что это соотношение не зависит от конкретного выбранного прямоугольного треугольника, если в нем есть угол A, поскольку такие треугольники будут подобные .

Косинус угла - это отношение длины прилежащего катета к длине гипотенузы. В нашем случае

cos ⁡ A = adjacent hypotenuse = b h. {\ Displaystyle \ cos A = {\ frac {\ textrm {adjacent}} {\ textrm {hypotenuse}}} = {\ frac {b} {h}} \ ,.}

Тангенс угла - это отношение длины противолежащего катета к длине прилегающего. В нашем случае

tan ⁡ A = opposite adjacent = a b. {\ Displaystyle \ tan A = {\ frac {\ textrm {opposite}} {\ textrm {adjacent}}} = {\ frac {a} {b}} \ ,.}

Обратные функции [ ред. | ред. код ]

Обратные тригонометрические функции используют, чтобы вычислить внутренние углы прямоугольного треугольника, если известны длины любых двух сторон.

Arcsin используют, чтобы вычислить угол, если известны длина противоположной стороны и длина гипотенузы

θ = arcsin ⁡ (opposite hypotenuse) {\ displaystyle \ theta = \ arcsin \ left ({\ frac {\ text {opposite}} {\ text {hypotenuse}}} \ right)}

Arccos используют, чтобы вычислить угол, если известны длина прилегающей стороны и длина гипотенузы

θ = arccos ⁡ (adjacent hypotenuse) {\ displaystyle \ theta = \ arccos \ left ({\ frac {\ text {adjacent}} {\ text {hypotenuse}}} \ right)}

Arctan используют, чтобы вычислить угол, если известны длины противоположной и прилегающей стороны

θ = arctan ⁡ (opposite adjacent) {\ displaystyle \ theta = \ arctan \ left ({\ frac {\ text {opposite}} {\ text {adjacent}}} \ right)}

На вступительной геометрии и уроках тригонометрии, часто используют обозначение sin-1, cos-1 и др. вместо arcsin, arccos и тому подобное. Однако обозначения arcsin, arccos и другие являются стандартными для высшей математики, где тригонометрические функции часто преподносят в степень, чтобы не путать обратный степень с обратной функцией .

Теоремы синусов, косинусов и тангенсов [ ред. | ред. код ]

теорема синусов Или правило синусов, [7] утверждает, что отношение длин сторон к синусов соответствующих противоположных углов есть величина постоянная, следовательно

a sin ⁡ α = b sin ⁡ β = c sin ⁡ γ. {\ Displaystyle {\ frac {a} {\ sin \ alpha}} = {\ frac {b} {\ sin \ beta}} = {\ frac {c} {\ sin \ gamma}}.}

Это отношение равно диаметру описанной окружности данного треугольника. Другая интерпретация теоремы утверждает, что каждый треугольник с углами α {\ displaystyle \ alpha} , Β {\ displaystyle \ beta} и γ {\ displaystyle \ gamma} подобен треугольника длина сторон которого равна sin ⁡ α {\ displaystyle \ sin \ alpha} , Sin ⁡ β {\ displaystyle \ sin \ beta} и sin ⁡ γ {\ displaystyle \ sin \ gamma} . Этот треугольник может быть построен, если начертить круг диаметром 1 и вписать в него два угла указанного треугольника. Длина сторон треугольника будет sin ⁡ α {\ displaystyle \ sin \ alpha} , Sin ⁡ β {\ displaystyle \ sin \ beta} и sin ⁡ γ {\ displaystyle \ sin \ gamma} . Сторона чья длина sin ⁡ α {\ displaystyle \ sin \ alpha} противоположна угла чья величина α {\ displaystyle \ alpha} И т. Д.

теорема косинусов Или правило косинусов, сочетает длину неизвестной стороны треугольника с длиной других сторон и с углом противоположным неизвестной стороны. Согласно теореме:

Для треугольника с длинами сторон a {\ displaystyle a} , B {\ displaystyle b} , C {\ displaystyle c} и углами α {\ displaystyle \ alpha} , Β {\ displaystyle \ beta} , Γ {\ displaystyle \ gamma} соответственно, для двух известных длин треугольника a {\ displaystyle a} и b {\ displaystyle b} И угла между двумя известными сторонами γ {\ displaystyle \ gamma} (Или угла противоположного неизвестной стороны c {\ displaystyle c} ), Чтобы рассчитать длину третьей стороны можно использовать следующую формулу:

c 2 = a 2 + b 2 - 2 ab cos ⁡ (γ) {\ displaystyle c ^ {2} \ = a ^ {2} + b ^ {2} -2ab \ cos (\ gamma)} b 2 = a 2 + c 2 - 2 ac cos ⁡ (β) {\ displaystyle b ^ {2} \ = a ^ {2} + c ^ {2} -2ac \ cos (\ beta)} a 2 = b 2 + c 2 - 2 bc cos ⁡ (α) {\ displaystyle a ^ {2} \ = b ^ {2} + c ^ {2} -2bc \ cos (\ alpha)}

Если длина всех трех сторон треугольника известна, тогда углы можно рассчитать по формулам:

α = arccos ⁡ (b 2 + c 2 - a 2 2 bc) {\ displaystyle \ alpha = \ arccos \ left ({\ frac {b ^ {2} + c ^ {2} -a ^ {2}} { 2bc}} \ right)} β = arccos ⁡ (a 2 + c 2 - b 2 2 ac) {\ displaystyle \ beta = \ arccos \ left ({\ frac {a ^ {2} + c ^ {2} -b ^ {2}} { 2ac}} \ right)} γ = arccos ⁡ (a 2 + b 2 - c 2 2 ab) {\ displaystyle \ gamma = \ arccos \ left ({\ frac {a ^ {2} + b ^ {2} -c ^ {2}} { 2ab}} \ right)}

теорема тангенсов или правило тангенсов, менее известное чем предыдущие два. Оно утверждает:

a - ba + b = tan ⁡ [1 февраля (α - β)] tan ⁡ [1 февраля (α + β)]. {\ Displaystyle {\ frac {ab} {a + b}} = {\ frac {\ tan [{\ frac {1} {2}} (\ alpha - \ beta)]} {\ tan [{\ frac { 1} {2}} (\ alpha + \ beta)]}}.}

Оно не очень часто используется, но может быть полезным когда нужно найти сторону или угол, когда известны две стороны и угол или два угла и сторона.

Еще формулы для треугольников Евклидовой геометрии [ ред. | ред. код ]

Для всех треугольников Евклидовой геометрии также справедливы следующие формулы:

3 4 (a 2 + b 2 + c 2) = ma 2 + mb 2 + mc 2 {\ displaystyle {\ frac {3} {4}} (a ^ {2} + b ^ {2} + c ^ { 2}) = m_ {a} ^ {2} + m_ {b} ^ {2} + m_ {c} ^ {2}}

и

ma = 1 2 2 b 2 + 2 c 2 - a 2 = 1 2 (a 2 + b 2 + c 2) - 3 апреля a 2 {\ displaystyle m_ {a} = {\ frac {1} {2}} {\ sqrt {2b ^ {2} + 2c ^ {2} -a ^ {2}}} = {\ sqrt {{\ frac {1} {2}} (a ^ {2} + b ^ {2} + c ^ {2}) - {\ frac {3} {4}} a ^ {2}}}} ,

и эквивалентно для mb {\ displaystyle m_ {b}} и mc {\ displaystyle m_ {c}} С соответствующими медианы и сторонами;

Длина внутренней биссектрисы α = 2 bcs (s - a) b + c = bc [1 - a 2 (b + c) 2] {\ displaystyle {\ text {длина внутренней биссектрисы}} \ \ \ alpha = {\ frac { 2 {\ sqrt {bcs (sa)}}} {b + c}} = {\ sqrt {bc [1 - {\ frac {a ^ {2}} {(b + c) ^ {2}}}] }}}

для полупериметр s, а длина биссектрисы измеряется с вершины угла до точки пересечения с противоположной стороной; в следующих формулах используется радиус описанной окружности R и радиус вписанной окружности r:

1 r = 1 ha + 1 hb + 1 hc {\ displaystyle {\ frac {1} {r}} = {\ frac {1} {h_ {a}}} + {\ frac {1} {h_ {b} }} + {\ frac {1} {h_ {c}}}}

если записать через высоты,

r R = 4 ⋅ S 2 sabc = cos ⁡ α + cos ⁡ β + cos ⁡ γ - 1 {\ displaystyle {\ frac {r} {R}} = {\ frac {4 \ cdot S ^ {2}} { sabc}} = \ cos \ alpha + \ cos \ beta + \ cos \ gamma 1} ,

и

2 R r = abca + b + c {\ displaystyle 2Rr = {\ frac {abc} {a + b + c}}} .

Допустим два смежных треугольника, не пересекаются, имеют общую сторону, длина которой f, и имеют общее описанная окружность таким образом, что сторона длиной f является хордой описанной окружности; треугольники имеют стороны с такими длинами (a, b, f) и (c, d, f), эти два треугольника вместе образуют вписан четырехугольник , А его стороны соответственно (a, b, c, d). тогда [8]

f 2 = (ac + bd) (ad + bc) (ab + cd). {\ Displaystyle f ^ {2} = {\ frac {(ac + bd) (ad + bc)} {(ab + cd)}}. \}

Пусть M - центроид треугольника с вершинами A, B, и C, и пусть P - любая внутренняя точка. Тогда расстояния между этими точками связаны [8]

(PA) 2 + (PB) 2 + (PC) 2 = (MA) 2 + (MB) 2 + (MC) 2 + 3 (PM) 2. {\ Displaystyle (PA) ^ {2} + (PB) ^ {2} + (PC) ^ {2} = (MA) ^ {2} + (MB) ^ {2} + (MC) ^ {2} 3 (PM) ^ {2}. \}

Пусть p a, p b, и p c - расстояния от центроида до сторон a, b, и c. тогда [8]

papb = ba, pbpc = cb, papc = ca {\ displaystyle {\ frac {p_ {a}} {p_ {b}}} = {\ frac {b} {a}} \ \ \ \ {\ frac { p_ {b}} {p_ {c}}} = {\ frac {c} {b}}, \ \ \ \ {\ frac {p_ {a}} {p_ {c}}} = {\ frac {c } {a}} \}

и

pa ⋅ a = pb ⋅ b = pc ⋅ c = 2 марта ⋅ S. {\ Displaystyle p_ {a} \ cdot a = p_ {b} \ cdot b = p_ {c} \ cdot c = {\ frac {2} {3}} \ cdot S. \}

Неплощинни треугольники [ ред. | ред. код ]

Неплощинни треугольники - это треугольники, находятся не на (плоской) плоскости. Примером такого треугольника в не-евклидовой геометрии является сферический треугольник Изучаемого в сферической геометрии и гиперболический треугольник в гиперболической геометрии .

Если сумма внутренних углов треугольника в плоскости всегда равна 180 °, то для гиперболического треугольника сумма углов будет меньше 180 °, а для сферического треугольника сумма углов будет больше 180 °. Гиперболический треугольник можно получить на отрицательно изогнутой поверхности, например гиперболический параболоид , А сферический треугольник можно получить на положительно изогнутой поверхности, например сфера . Таким образом, если изобразить гигантский треугольник на поверхности Земли, то получим сумму углов больше чем 180 °; фактически сумма будет лежать в промежутке 180 ° и 540 ° [9] В частности можно изобразить треугольник на сфере таким образом, что каждый внутренний угол будет равен 90 °, а сумма всех углов 270 °.

В частности, на сфере сумма углов треугольника равна

180 ° × (1 + 4 f),

где f - это отношение площади сферы к площади ограниченной треугольником. Например, предположим мы изобразим треугольник на поверхности Земли (будем считать, что Земля это сфера, что на самом деле не совсем так ) С вершинами на Северном полюсе, на точке экватора с широтой 0 °, и точка на экваторе 90 ° западной долготы. линия большого круга между упомянутыми двумя точками будет экватор, а линия большого круга между каждой из этих двух точек и Северным полюсом будет линией меридиана; следовательно получим прямые углы на экваторе. Более того, угол на Северном полюсе также 90 ° так как предыдущие две вершины различаются на 90 ° по долготе. Сумма углов в этом треугольнике - 90 ° 90 ° 90 ° = 270 °. Этот треугольник покрывает 1/4 северного полушария (90 ° / 360 ° если смотреть с Северного полюса) и соответственно 1/8 земной поверхности, тогда подставляем в формулу f = 1/8; как видим формула дает правильный результат 270 °.

Из формулы выше мы также видим, что в определенном приближении поверхность земли можно считать плоской, если изобразить произвольный малый треугольник на поверхности Земли, тогда доля f земной поверхности, ограниченной данным треугольником будет близка к нулю. Например, известно, что площадь земной поверхности 510 млн км², тогда для треугольника площадью 10 000 км², получим сумму углов 180.01 °.

Теоремы и утверждения о треугольники

1. ↑ Weisstein, Eric W. Triangle (Англ.) На сайте Wolfram MathWorld .
2. ↑ Benyi, Arpad, "A Heron-type formula for the triangle,« Mathematical Gazette »87 July 2003, 324-326.
3. ↑ Mitchell, Douglas W., "A Heron-type formula for the reciprocal area of a triangle ," Mathematical Gazette 89, November 2005, 494.
4. ↑ Mitchell, Douglas W., "A Heron-type area formula in terms of sines," Mathematical Gazette 93, March 2009, 108-109.
5. ↑ Mitchell, Douglas W., "The area of a quadrilateral," Mathematical Gazette 93, July 2009, 306-309.
6. ↑ Baker, Marcus, "A collection of formulae for the area of a plane triangle ," Annals of Mathematics, part 1 in vol. 1 (6), January 1885, 134-138; part 2 in vol. 2 (1), September 1885, 11-18.
7. ↑ Prof. David E. Joyce. The Laws of Cosines and Sines . Clark University. Архив оригинала 2013-06-22.
8. ↑ а б в Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
9. ↑ Watkins, Matthew, Useful Mathematical and Physical Formulae, Walker and Co., 2000.

• Г. П. Бевз. Геометрия треугольника. - Киев: Генезис, 2005, ISBN 966-504-431-1
• Бевз Г. П., Бевз В.Г., Владимирова Н. Г. Геометрия: Учебник для 7-9 кл. - Киев: Башня, 2004, ISBN 966-7091-66-Х.
• И. А. Кушнир. Треугольник и тетраэдр в задачах. - Киев: Радянська школа, 1991, ISBN 5-330-02081-6
• И. А. Кушнир. Возвращение потерянной геометрии. - Киев: Факт, 2000 ISBN 966-7274-75-5
• Погорелов А.В. Геометрия. Учебник. для 7 - 9 кл. - Киев: Школьник, 2004

Похожие

Комментарии