Точные значения триггеров

1. Таблица точных значений Trig
2. Все тригональные функции на одной диаграмме
3. Триггерные функции углов вне диапазона от 0 ° до 90 °
4. Узоры
5. Шаблон √ 2 ± √n
6. Модель √ 2 ± Фи
7. Доказательств
8. 36 ° и 54 °, 18 ° и 72 °
9. 15 ° и 75 °
10. Ailles Rectangle для 15 ° и 75 °
11. Еще один прямоугольник на 22,5 °
12. Диаграмма, чтобы связать много углов и Phi
13. Вы делаете математику ...
14. Другие углы с точными выражениями триггеров с квадратными корнями
15. сращивание
16. Накладывая
17. Мы знаем все углы?
18. Формула π / 17
19. Формула π / 15
20. Trig Calculator с использованием десятичных чисел любой длины
21. Рекомендации

Эта страница о тригонометрических функциях синуса, косинуса и тангенса, о том, что они из себя представляют и как найти точные значения многих углов.

Калькуляторы и другие эффекты на этой странице требуют JavaScript, но вы, кажется, отключили JavaScript (он отключен) в этом браузере.
Перейдите к пункту «Настройки» или «Свойства» для этого браузера и включите его, а затем перезагрузите эту страницу.

Какие углы имеют точное выражение для их синусов, косинусов и касательных? Возможно, вы знаете, что cos (60 °) = 1/2 и sin (60 °) = √3 / 2, а также tan (45 °) = 1, но 30, 45 и 60 - это единственные углы до 90 ° с формула для их значений триггера? Нет! Есть намного больше, но не все углы имеют точные выражения, включающие не более чем квадратные корни.
Какие углы делают? Какие шаблоны присутствуют в этих выражениях? Эта страница показывает выражения для многих углов и даже решает полную проблему, какие углы делают, а какие не имеют таких точных выражений триггера.

Таблица точных значений Trig

которые можно выразить как простые термины, включающие квадратные корни. a cos (a)
грех (б) загар (а)
кроватка (б) б радианы ° ° радианы 0 0 1 0 90 π
2 π
24 7.5 `(sqrt (2 + sqrt (2 + sqrt 3)))) / 2`` sqrt 6 - sqrt 3 + sqrt 2 - 2`
`= (sqrt 2 - 1) (sqrt 3 - sqrt 2)` 82,5 11 π
24 π
12 15 `(sqrt 6 + sqrt 2) / 4 = sqrt (1/2 + (sqrt 3) / 4) = sqrt ((4+ sqrt 12) / 8)`
`2-sqrt 3`
75 5 π
12 cos2 (15 °) = [0; 1,13, 1,12] tan (15 °) = [0; 3, 1, 2]
tan2 (15 °) = [0; 13, 1, 12] π
10 18 `sqrt (10 + 2 sqrt 5) / 4 = sqrt ((5 + sqrt 5) / 8)`
`sqrt (1- (2 sqrt 5) / 5)` 72 2 π
5 cos2 (18 °) = [0; 1, 9, 2, 8] tan2 (18 °) = [0; 9, 2,8] π
8 22,5 `(sqrt (2 + sqrt 2)) / 2 = sqrt ((4 + sqrt 8) / 8)` `sqrt 2 - 1` 67,5 3 π
8 cos2 (22,5 °) = [0; 1, 5, 1, 4] tan (22,5 °) = [0; 2]
tan2 (22,5 °) = [0; 5, 1, 4] π
6 30 `(sqrt 3) / 2`` (sqrt 3) / 3` 60 π
3 cos (30 °) = [0; 1, 6, 2, 6]
cos2 (30 °) = [0; 1,3] загар (30 °) = [0; 1, 1, 2]
tan2 (30 °) = [0; 3] π
5 36 `(sqrt 5 + 1) / 4 = sqrt ((3 + sqrt 5) / 8)` `sqrt (5 - 2 sqrt 5)` 54 3 π
10 cos (36 °) = [0; 1, 4]
cos2 (36 °) = [0; 1, 1, 1, 8, 2] tan2 (36 °) = [0; 1, 1, 8, 2] 5 π
24 37,5 `sqrt (2 + sqrt (2 - sqrt 3)) / 2` `sqrt 6 + sqrt 3 - sqrt 2 - 2`
`= (sqrt 2 + 1) (sqrt 3 - sqrt 2)` 52,5 7 π
24 π
4 45 `sqrt 2 / 2`` 1` 45 π
4 cos (45 °) = [0; 1, 2]
cos2 (45 °) = [0; 2] 7 π
24 52,5 `(sqrt (2 - sqrt (2 - sqrt 3)))) / 2`` sqrt 6 - sqrt 3 - sqrt 2 + 2`
`= (sqrt 2 - 1) (sqrt 3 + sqrt 2)` 37,5 5 π
24 3 π
10 54 `(sqrt (10 - 2 sqrt 5)) / 4 = sqrt ((5 - sqrt 5) / 8)` `sqrt ((5 + 2 sqrt 5) / 5)` 36 π
5 cos2 (54 °) = [0; 2, 1, 8, 2] tan2 (54 °) = [1; 1, 8, 2] π
3 60 `1 / 2`` sqrt 3` 30 π
6 cos (60 °) = [0; 2]
cos2 (60 °) = [0; 4] загар (60 °) = [1; 1, 2]
tan2 (60 °) = 3 3 π
8 67,5 `sqrt (2-sqrt 2) / 2 = sqrt ((4-sqrt 8) / 8)` `1 + sqrt 2` 22,5 π
8 cos2 (67,5 °) = [0; 6, 1, 4] tan (67,5 °) = [2; 2]
tan2 (67,5 °) = [5; 1, 4] 2 π
5 72 `(sqrt 5 - 1) / 4 = sqrt ((3-sqrt 5) / 8)` `sqrt (5 + 2 sqrt 5)` 18 π
10 cos (72 °) = [0; 3, 4]
cos2 (72 °) = [0; 10, 2, 8] tan2 (72 °) = [9; 2, 8] 5 π
12 75 `(sqrt 6 - sqrt 2) / 4 = sqrt (1/2 - sqrt 3/4) = sqrt ((4 - sqrt 12) / 8)` `2 + sqrt 3` 15 π
12 cos2 (75 °) = [0; 14, 1, 12] загар (75 °) = [3; 1, 2]
tan2 (75 °) = [13; 1, 12] 11 π
24 82,5 `sqrt (2 - sqrt (2 + sqrt 3)) / 2`` sqrt 6 + sqrt 3 + sqrt 2 + 2`
`= (sqrt 2 + 1) (sqrt 3 + sqrt 2)` 7.5 π
24 π
2 90 `0`` oo` 0 0 Продолжение дроби [a; b, c, d, ...] является сокращенной записью для
и периодическая непрерывная дробь [а; b, c, d, e, d, e, d, e, ...] записывается как [a; б, в, д, е]
где любое число перед точкой с запятой (;) является целой частью, а линия над числами указывает часть, которая повторяется навсегда в конце.
Увидеть Введение в продолжение фракций ,

Все тригональные функции на одной диаграмме

Вот это действительно здорово Mathematica демонстрация взаимосвязи всех 6 тригонометрических функций на одной интерактивной диаграмме. Вот статичное изображение, которое в любом случае является полезной диаграммой:

Тем не менее, диаграмма полезна для просмотра того, что измеряется шестью функциями, но она не дает никаких признаков знаков значений.
Знаки выбраны, чтобы сделать формулу триггера увидеть ниже последовательный для всех углов. Кроме того, в следующем разделе показаны их графики, а из основного графика SINE следуют все остальные.
Функция синуса имеет много применений в механике (например, движения вращающихся объектов), электронике (например, переменный электрический ток и электромагнитные волны), ....

Триггерные функции углов вне диапазона от 0 ° до 90 °

Вот диаграммы угла в каждом из четырех квадрантов круга, снимки с превосходного Как связаны функции тригонометрии из демонстрационного проекта Wolfram C. Ormullion. Нажмите в квадранте, чтобы увидеть типичный угол и все 6 тригонометрических функций.
Вот еще одна визуализация с помощью графиков: хороший способ запомнить SIGN для использования для функций в каждом квадранте состоит в том, что все они положительны в первых квадрантах (0-90 °), но в других квадрантах только один из грехов, cos или tan положительны в других секторах:
Синь
Все еще
C osine
Вы можете видеть, что он написан внутри большого знака PLUS (+), и единственная функция (и), имеющая знак плюс со своими значениями в этом квадранте, находится в порядке угловой стороны:
« Все , время, тосканец», и вы можете вспомнить это с глупой рифмой « Все, что угодно».

Но почему бы не написать свою СОБСТВЕННУЮ фразу, чтобы запомнить буквы ASTC ?
Если это глупо, то вы, скорее всего, запомните это!

Как только вы помните знак для этих трех функций, вы можете использовать тот же знак для их взаимных значений Cosecant, Secant и Cotangent.

Все основные формулы здесь отвечают на графике SINE следующим образом:

• Синус угла определяется вертикальной высотой точки, когда она вращается вокруг единичной окружности (то есть ее радиус равен 1), измеренной от горизонтальной линии, проходящей через центр окружности. Поэтому оно не может быть больше 1 или меньше -1.
• косинус угла определяется горизонтальным расстоянием точки, когда оно вращается вокруг единичного круга, измеренного от вертикальной линии через центр круга. Это тоже должно быть в диапазоне от -1 до 1.
• Из диаграммы легко увидеть, что графики синусов и косинусов имеют одинаковую форму , но смещены на четверть оборота (90 °). В математических терминах мы бы сказали, косинус (х) = синус (90 ° + х).
• Тангенс угла измеряет отношение синуса к косинусу и может принимать любое значение.
  При кратности 90 ° оно становится бесконечным или отрицательно бесконечным.

Нажмите на диаграмму, чтобы перейти к Mathematica Демонстрационный сайт для бесплатного формата вычислимых документов ( CDF ) версия, которая воспроизводится в бесплатном проигрывателе CDF и позволяет оживить анимацию.
Демонстрация синуса и косинуса, проводимая компанией B Atwood и S Wagon.

Углы могут быть измерены несколькими типами единиц измерения.

• Часто это градусы с полным поворотом, разделенным на 360 градусов
• Если мы определяем синус и косинус по расстояниям (или координатам) точки на единичной окружности, мы также можем определить угол по расстоянию и по этой окружности: расстояние по окружности, по которому точка проходит в тьюринге через этот угол. Окружность единичного круга составляет 2 π. Эта мера называется радианой .

Вот конвертер для преобразования между ними:

Узоры

Простая модель квадратного корня

Эрнесто Ла Орден из Мадрида указал на следующий аккуратный способ соединения и запоминания самого простого из синусов (косинусов): ° рад косинус синус ° рад 0 0 90 π
2 30 π
6 60 π
3 45 π
4 45 π
4 60 π
3 30 π
6 90 π
2 0 0

Шаблон √ 2 ± √n

Эрнесто Ла Орден также поместил много углов в эту схему: ° косинус синус ° 90 0 75 15 67,5 22,5 60 30 45 45 30 60 22,5 67,5 15 75 0 90

Модель √ 2 ± Фи

° косинус / й> синус ° 72 $$ \ frac {\ sqrt {2 - \ Phi}} {2} $$ 18 54 $$ \ frac {\ sqrt {2 - \ varphi}} {2} $$ 36 36 $$ \ frac {\ sqrt {2 + \ varphi}} {2} $$ 54 18 $$ \ frac {\ sqrt {2 + \ Phi}} {2} $$ 72 \ (Phi = \ Phi = \ frac {\ sqrt {5} + 1} {2} = 1.618033 ... = 1 + \ varphi \)
\ (phi = \ varphi = \ frac {\ sqrt {5} - 1} {2} = 0.618033 .. = \ Phi - 1 \)
\ (Phi ^ {\, 2} = \ Phi ^ 2 = \ frac {3+ \ sqrt {5}} {2} = 2.618033 .. \)
\ (phi ^ {\, 2} = \ varphi ^ 2 = \ frac {3 - \ sqrt {5}} {2} = 0.381966 ... \) Мы можем расширить предыдущий шаблон, включив в него множество углов, которые являются простыми дробями из π, если мы используем золотое сечение значения Phi (\ (\ Phi \)) и phi (\ (\ varphi \)): cos (9 ° = π / 20) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 + \ Phi}} \) = sin (81 °) cos (18 ° = π / 10) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 + \ varphi}} = \ frac {1} {2} \ sqrt {2 + \ Phi} \) = sin (72 °) cos (27 ° = 3 π / 20) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 - \ varphi}} \) = sin (63 °) cos (36 ° = π / 5) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 - \ Phi}} = \ frac {1} {2} \ sqrt {2 + \ varphi} = \ frac {\ Phi} {2} \) = sin (54 °) cos (45 ° = π / 4) = \ (\ frac {1 } {2} \ sqrt {2 \ pm \ sqrt {2 - 2}} = \ frac {\ sqrt {2}} {2} \) = sin (45 °) cos (54 ° = 3 π / 10) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 - \ Phi}} = \ frac {1} {2} \ sqrt {2 - \ varphi} \) = sin (36 °) cos (63 ° = 7 π / 20) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 - \ varphi}} \) = sin (27 °) cos (72 ° = 2 π / 5) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 + \ varphi}} = \ frac {1} {2} \ sqrt {2 - \ Phi} = \ frac {\ varphi } {2} \) = sin (18 °) cos (81 ° = 9 π / 20) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 + \ Phi}} \) = грех (9 °) Этот шаблон использует тождества

\ (phi = \ varphi = \ sqrt {2 - \ Phi} \) и \ (Phi = \ Phi = \ sqrt {2 + \ varphi} \)

Здесь есть более всеобъемлющий шаблон, если мы используем все следующие значения под самым внутренним квадратным корнем:

\ (2, \ sqrt {3}, \ Phi, 1, \ varphi, 0, - \ varphi, -1, - \ sqrt {3}, - \ Phi, -2 \)
или же
2, 1,732 ..., 1,618 ..., 1, 0,618 ..., 0, -0,618 ..., -1, -1,618 ..., -1,732 ..., -2

вместе с формулой полуугольника для cos (A / 2) (см. ниже), начиная с cos (36) = Phi / 2 и cos (72) = phi / 2. Схема продолжается с косинусами 4,5 °, 13,5 ° и т. Д. И включает в себя следующие углы, которые также являются долями π: cos (0) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 + 2}} = 1 \) sin (90 °) cos (7,5 ° = π / 24) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 + \ sqrt {3} }} \) sin (82,5 °) cos (37,5 ° = 5 π / 24) = \ (\ frac {1} {2} \ sqrt {2 + \ sqrt {2 - \ sqrt {3}}} \) sin (52,5 °) cos (45 ° = π / 4) = \ (\ frac {1} {2} \ sqrt {2 \ pm \ sqrt {2 - 2}} = \ frac {\ sqrt {2}} {2 } \) sin (45 °) cos (52,5 ° = 7 π / 24) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 - \ sqrt {3}}} \) sin ( 37,5 °) cos (82,5 ° = 11 π / 24) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 + \ sqrt {3}}} \) sin (7,5 °) cos ( 90 ° = π / 2) = \ (\ frac {1} {2} \ sqrt {2 - \ sqrt {2 + 2}} = 0 \) sin (0 °)

Доказательств

30 ° 45 ° и 60 °

Вот два простых треугольника, которые дают нам формулы для значений триггера этих трех углов:

36 ° и 54 °, 18 ° и 72 °

Для 36 ° и 72 ° нам потребуется дополнительная работа, основанная на геометрии правильного пятиугольника, который имеет углы 36 ° и 72 °. Если стороны пятиугольника имеют длину 1, диагонали имеют номер золотого сечения длиной Phi, где: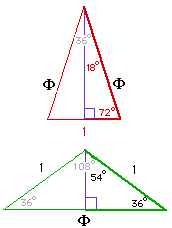
Верхний треугольник с углами 72 °, 72 ° и 36 ° и сторонами длиной 1, Phi и Phi показывает значения триггера для 18 ° и 72 °.

Нижний треугольник с углами 36 °, 36 ° и 108 ° и сторонами длиной 1, 1 и Phi показывает значения триггера 36 ° и 54 °.

15 ° и 75 °

Если мы возьмем треугольник слева, мы можем рассчитать длину третьей стороны, используя формулу косинуса . Если в треугольнике со сторонами a, b и c мы знаем обе стороны b и c, а также угол A между сторонами b и c, то мы можем вычислить длину третьей стороны a следующим образом:

Ailles Rectangle для 15 ° и 75 °

Альтернативный (более простой) метод для синуса и косинуса 15 ° и 75 ° найден в прямоугольнике Эйлла (названного в честь учителя средней школы Онтарио). Его легко запомнить, потому что он двухцветный) 45-градусные прямоугольные треугольники, прикрепленные по бокам белого треугольника 30-60-90, и прямоугольник, дополненный желтым треугольником 15-75-90 на гипотенузе 30-60- 90 треугольник, как показано здесь.
30-60-90 сторон "как обычно", а именно `1, 2` и` √3`. Из двух 45-45-90 треугольников довольно легко увидеть, что `x` это` sqrt 3 / sqrt 2`, а `y` это` 1 / sqrt 2`, из которого мы можем прочитать синусы и косинусы 15 ° и 75 °. Однако мы получим более хорошие числа на треугольниках, если расширим все стороны с коэффициентом `sqrt 2`. Нажмите на кнопки под изображением, чтобы увидеть (расширенные) размеры.

Еще один прямоугольник на 22,5 °

Триг Формулы

Многие симметрии и модели очевидны в таблице. Они отражают некоторые основные особенности, такие как:

Если мы знаем значение функции триггера под двумя углами `a` и` b`, мы можем определить значения функции триггера их суммы и разности, используя следующие тождества:

`Sin (а ​​+ б) = Sin (а) соз (б) + соз (а) Sin (б)`
`cos (a + b) = cos (a) cos (b) -sin (a) sin (b)` `tan (a + b) = (tan (a) + tan (b)) / (1-tan (а) tan (b)) `` sin (ab) = sin (a) cos (b) -cos (a) sin (b) `
`cos (ab) = cos (a) cos (b) + sin (a) sin (b)` `tan (ab) = (tan (a) -tan (b)) / (1 + tan (a) tan (б)) `

Если два угла одинаковы (то есть `a = b`), мы получаем синусы и косинусы двойного угла. Перестановка этих формул дает формулу для греха или косинуса половины угла:

`sin (2a)` `= 2sin (a) cos (a)` `sin (a / 2) = sqrt ((1-cos (a)) / 2)` `cos (2a)` `= 1-2sin ^ 2 (a) `` cos (a / 2) = sqrt ((1 + cos (a)) / 2) `` = cos ^ 2 (a) -sin ^ 2 (a) `` = 2 cos ^ 2 (a) -1` `2 csc (2a) = tan (a) + cot (a)` `tan (a / 2) = (1-cos (a)) / sin (a) = sin (a) / (1 + соз (а)) `
Следующее изменяет произведение тригонометрических функций на сумму или разность и наоборот: `sin (a) + sin (b)` `= 2 cos ((ab) / 2) sin ((a + b) / 2) `` cos (a) + cos (b) `` = 2 cos ((ab) / 2) cos ((a + b) / 2) `` sin (a) - sin (b) `` = 2 sin ( (ab) / 2) cos ((a + b) / 2) `` cos (b) - cos (a) `` = 2 sin ((ab) / 2) sin ((a + b) / 2) `

Диаграмма, чтобы связать много углов и Phi

Страница Роберта Грея на Координаты для многих регулярных тел имеет удивительную диаграмму внизу, которая соотносит фи с углами 18 °, 30 °, 36 °, 45 °, 54 °, 60 ° и 72 ° в соответствии с их трехмерными координатами в твердых телах.

Каждый из этих углов измеряется от самой верхней точки круга, когда вертикальная линия поворачивается на этот угол.
Каждая линия от базовой точки встречает окружность в точке, высота которой составляет 1 (72 °), 1 + Фи (60 °), 2 + Фи (54 °), 2 + 2 Фи (45 °), 2 + 3 Фи (36 °), 3 + 3 Фи (30 °) или 3 + 4 Фи (18 °).

Посмотрите на его страницы для получения более интересной информации о 120 трехмерных телах, из которых мы также рассмотрим наиболее симметричные 5 на нашем следущая страница ,

Вы делаете математику ...

1. Предположим, что начало круга (0,0) и его радиус 2 + 2 Фи. Найти уравнение круга.
2. Используйте свой ответ на предыдущий вопрос, чтобы найти координаты каждой из точек на окружности с указанными углами.
3. Вычислите длины каждой из красных линий от самой нижней точки до точек, показанных на круге.
4. 

   Из любых двух точек A и B на окружности угол AOB в центре круга, O, в два раза больше угла в любой точке окружности в том же секторе.

   На диаграмме все красные углы на окружности равны;
   красные углы - половина синего угла AOB в центре;
   красные углы находятся в той же точке круга, что и центр круга, поэтому они не могут находиться в сером секторе.
   

   Используйте приведенную выше теорему, чтобы найти три Круг Роберта Грея непосредственно перед этим разделом «Вы делаете математику ...», где линия от центра составляет угол с вертикалью
   1. 2 × 18 = 36 °
   2. 2 × 30 = 60 & deg;
   3. 2 × 36 = 72 °

Другие углы с точными выражениями триггеров с квадратными корнями

Есть ли другие углы с простым точным выражением их косинуса или синуса?
Ну, все зависит от того, что вы подразумеваете под простым !

Карл Фридрих ГАУСС (177 - 1855) рассмотрел аналогичную проблему, которая отвечает на этот вопрос. Он исследовал, существует ли метод построения правильного многоугольника из n сторон, используя только пару компасов (для рисования окружностей) и прямой край (линейка без разметки). Мы знаем, что можем построить правильный многоугольник для всех значений n = 3, 4, 5, 6, 8 и 10.

сращивание

Существует простой геометрический способ использования компасов для деления угла на два (деление угла на части). Таким образом, все углы в правильном n-гоне можно разделить на два, чтобы получить правильный 2-угольник. Мы можем повторить процесс, чтобы получить 4n-гон, 8n-гон и вообще 2kn-гон для любого k, если у нас есть метод построения регулярного n-гона.

Приведенный выше раздел «Формула триггера» содержит формулу для косинуса половины угла в терминах косинуса (целого) угла:

`cos (A / 2) = sqrt ((1 + cos (A)) / 2) = (sqrt (2 + 2 cos (A))) / 2`

Как указал мне Митч Уайетт, поскольку мы знаем, что cos (90 °) равно 0, а 90 ° - это π / 2 радиана, мы можем использовать его для нахождения косинуса половины этого угла (45 ° или π / 4 радиана) и затем снова разделить этот угол пополам и так далее. Каждый раз, когда мы вводим еще один квадратный корень, мы получаем каскадную или вложенную последовательность квадратных корней: `cos (pi / 4) =` `(sqrt 2) / 2`
`cos (pi / 8) =` `(sqrt (2 + sqrt 2)) / 2`
`cos (pi / 16) =` `(sqrt (2 + sqrt (2 + sqrt 2))) / 2`
`cos (pi / 32) =` `(sqrt (2 + sqrt (2 + sqrt (2 + sqrt 2)))) / 2` Однако эта страница посвящена синусам и косинусам, которые имеют более простые выражения, поэтому мы не будем развить это, разве что сказать, что это показывает, как мы всегда можем найти точное выражение для синуса (или косинуса) `1/2, 1/4, 1/8, ..., 1/2 ^ n` любого угол, для которого мы имеем точное выражение синуса (или косинуса).

Накладывая

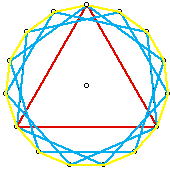
Если мы построим правильный треугольник (3 стороны) и с одним и тем же центром круга, построим три правильных пятиугольника (5 сторон), каждый из которых будет иметь одну общую вершину с треугольником, у нас будет 15 вершин правильного 15-угольника.
Это показано справа с тремя пятиугольниками синего цвета на одном круге, каждый из которых имеет общую вершину с красным треугольником, а обычный 15-угольник отображается желтым цветом.
Путем наложения двух правильных многоугольников, подобных этому, мы можем построить правильный P × Q-угольник (если P и Q не имеют общих множителей, иначе более одной вершины каждого из них будет совпадать).

Мы знаем все углы?

Все это было известно в Евклид Время около 300 г. до н. Так что насчет 7-го и 9-го? Можно ли найти синусы и косинусы всех кратных 1/7 и 1/9 оборота в точном выражении (используя квадратные корни)? А как насчет 11-го и 12-го и т. Д.?

В последующие 2000 лет никто не нашел точного геометрического метода для 7-гонов или 9-гонов, но также никто не доказал, что невозможно построить такие правильные многоугольники.

затем CF Gauss полностью решил проблему, когда он был студентом в Геттингене между 1795 и 1798 годами. Гаусс нашел условия на n и его основные факторы для решения двух эквивалентных задач:

• рисование правильного n-стороннего многоугольника, используя только прямой край и компас и
• выражая cos и sin 360 / n °, используя только квадратные корни.

Если мы рассмотрим n как 2ap1bp2c ..., то есть a, b, c, ... - степени простых множителей n: 2, p1, p2, ... (степень простого числа равна n, если она не является фактор п), то обе проблемы разрешимы, когда

• b, c, ... и все силы, кроме a , степень 2 , должна быть 1, и
• простые числа> 2, которые являются множителями n (то есть p1, p2, ...), должны иметь форму 22k + 1 для некоторого числа k.

Обе проблемы разрешимы для этих значений n и только для этих значений.

Простые числа вида 22k + 1 называются Ферма простые числа , Начинается серия чисел вида 22к + 1

220 + 1 = 3, 221 + 1 = 5, 222 + 1 = 17, 223 + 1 = 257, 224 + 1 = 65537, ...

Однако не каждое число вида 22k + 1 является простым - и только простые числа мы должны иметь как множители n.
Следующий 225 + 1 равен 4294967297 и имеет коэффициент 641, поэтому он не прост . На самом деле, мы не знаем, есть ли еще какие-либо простые числа этой формы, кроме первых 5, перечисленных выше.

Такие числа n в форме, описанной Гауссом, следующие: по одному на строку, каждое из которых является произведением некоторых простых чисел Ферма (но каждое простое не более одного раза), за которыми следуют его кратные два. Для любого числа в таблице его двойник также находится в таблице:

2 4 8 16 32 64 128 256 ... 3 6 12 24 48 96 192 ... 5 10 20 40 80 160 ... 3 × 5 = 15 30 60 120 240 ... 17 34 68 136 272 ... 3 × 17 = 51 102 204 408 ... 5 × 17 = 85 170 340 680 ... 3 × 5 × 17 = 255 510 1020 2040 ... 257 514 1028 2056 ... При заказе мы имеем

(1), 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102 ...

который Слоана A003401 ,

Нечетные термины (левый столбец, кроме 2) - это ряд

1, 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295

который A045544 поскольку мы не знаем больше простых чисел Ферма, кроме пятого (65537).

Некоторые интересные факты об этих нечетных числах (мы также включаем 1 здесь):

• все эти 31 нечетное число являются делителями 225–1 = 232 - 1 = 4294967295 (см. A004729 )

Когда они записаны в двоичном коде, они все палиндромные (в точности наоборот).
Если мы продолжим этот паттерн, независимо от того, является ли 22k – 1 простым или нет, то мы обнаружим паттерн треугольника Серпинского. Это фрактал - меньшие версии самого себя содержатся во всех больших версиях. Один из способов его формирования - изобразить четность (нечетность и четность) чисел в треугольнике Паскаля, где каждое нечетное число в треугольнике Паскаля представлено черным квадратом, а каждое четное число - белым: в треугольнике Паскаля мы можем начать с верхнего ряда 0 (белый) с одним элементом 1 (нечетный, черный) в нем.
Затем для строк ниже мы можем использовать правило, согласно которому каждый элемент создается путем сложения двух элементов в строке выше:
один прямо над, а другой справа. 1 4+ 6 4 1 ↓ 1 5 10 10 5 1 На диаграммах здесь мы хотим только четность элемента (нечетного или четного), поэтому мы имеем простое правило, что если оба элемента в строке выше одинаковы цвет:
оба черные (нечетные) или оба белые (четные)
элемент будет белым (четным), если два элемента в строке выше отличаются
один нечетный, один четный
элемент черный (нечетный)

Формула π / 17

Другая малая дробь знаменателя, которую мы еще не рассмотрели, - это доказанная Гауссом формула с квадратными корнями для косинусов и синусов, кратных \ (\ frac {\ pi} {17} \) радиан.
Формулы, созданные и упрощенные с помощью Mathematica® все еще довольно сложны. Например, здесь \ (cos (\ frac {\ pi} {17}) \)
`cos (pi / 17)` `= sqrt (15 + sqrt 17 + sqrt (34 - 2 sqrt 17) + sqrt (68 + 12 sqrt 17 - 4 sqrt (170 + 38 sqrt 17)))) / (4 sqrt ( 2)) `` = 0.98297309968390177828194884485 ... `Мультипликаторы этого угла также включают вариации тех же 4 выражений, которые мы видим здесь. Каждая из четырех форм, A, B, C, D, является суммой или разностью тех же двух слагаемых.
Мы будем использовать индекс + или - в качестве сокращения для знака, используемого в каждом варианте. Вот они все:
`A _ (+) = 15 + sqrt (17)` `A _ (-) = 15 - sqrt (17)` `B _ (+) = sqrt (2) sqrt (17 + sqrt (17))` `B _ (- ) = sqrt (2) sqrt (17 - sqrt (17)) `` C _ (+) = 17 + 3 sqrt (17) `` C _ (-) = 17 - 3 sqrt (17) `` D _ (+) = sqrt (2) sqrt (85 + 19 sqrt (17)) `` D _ (-) = sqrt (2) sqrt (85 - 19 sqrt (17)) `Выражения для косинусов и знаков, кратных углам π / 17 = 33.2639222145 .. ° до 90 ° = π / 2 радиана: a √32 cos2 (a) \ (\ color {red} \ frac {\ pi} {17} \) `A _ (+) + B_ (+) + 2 sqrt (C _ (+) - D _ (+)) `\ (\ color {red} \ frac {2 \ pi} {17} \)` A _ (+) - B _ (-) + 2 sqrt (C _ (+) + D _ (+)) `\ (\ color {red} \ frac {3 \ pi} {17} \)` A _ (-) + B _ (+) + 2 sqrt (C _ (-) + D _ (-)) `\ (\ color {red} \ frac {4 \ pi} {17} \)` A _ (+) + B _ (-) - 2 sqrt (C _ (+) - D _ (+)) ` \ (\ color {red} \ frac {5 \ pi} {17} \) `A _ (-) + B _ (+) - 2 кв. (C _ (-) + D _ (-))` \ (\ color {red } \ frac {6 \ pi} {17} \) `A _ (-) - B _ (+) + 2 sqrt (C _ (-) - D _ (-))` \ (\ color {red} \ frac {7 \ pi} {17} \) `A _ (-) - B _ (+) - 2 sqrt (C _ (-) - D _ (-))` \ (\ color {red} \ frac {8 \ pi} {17} \ ) `A _ (+) - B _ (-) - 2 sqrt (C _ (+) + D _ (+))` Фу!

Следующее значение с нечетным знаменателем - π / 257, и точное выражение для cos (π / 257), использующее только квадратные корни, будет еще более сложным!

Том Эйс отметил, что об этом есть больше в главе 15 «Теории чисел Ойстейн-Руды и ее истории с 1948 года». теперь доступно как книга Дувра (1988).

Формула π / 15

Если `A _ (+) = 9 + sqrt 5`` A _ (-) = 9 - sqrt 5` `B _ (+) = sqrt (6 (5 + sqrt 5))` `B _ (-) = sqrt (6 ( 5-sqrt 5)) `тогда мы имеем 4cos2 (a) π
15 `A _ (+) + B _ (-)` 2π
15 `A _ (-) + B _ (+)` 4π
15 `A _ (+) - B _ (-)` 7π
15 `A _ (-) - B _ (+)`

Trig Calculator с использованием десятичных чисел любой длины

Вот Калькулятор это позволит вам проверять все вышеприведенные результаты и даже больше, сколько угодно десятичных знаков, а также оценивать выражения и находить непрерывные дроби.
Например, чтобы проверить формулу `cos (pi / 17)` выше тип
в поле ввода выражения для оценки, а затем нажмите кнопку преобразования ( ) и получить его десятичное значение, которое равно 0.

Для других значений, таких как `cos (pi / 8)`, введите и оцените его сначала как десятичную, а затем как непрерывную дробь, показывающую, что CF равен [0; 1, 12, 7, 3, 2, 1, 1, 1, 1, 20, 5, 3, 11, 1, 7, 7, 3, ...]. Даже если заглянуть в будущее для многих других терминов, здесь нет закономерности
Однако, если мы изменим выражение на Evaluate на CF, это время будет [0; 1, 5, 1, 4, 1, 4, 1, 4, 1, 4, 1, 4, ...].
Здесь есть четкая закономерность для многих терминов. Если мы удалим часть 1,4,1,4, ... и поместим ее во входные данные повторяющейся части для CF, чтобы у вас был CF [0; 1, 5, 1, 4], а затем нажмите кнопку преобразования в дробную форму ( ) покажет `(2 + sqrt (2)) / 4` в качестве значения` cos (pi / 8) ^ 2`, поэтому мы выводим, что (в вычислительном отношении) `cos (pi / 8) = sqrt (2 + sqrt (2)) / 2`.

Таким образом, мы можем экспериментально обнаружить много таких выражений для триг-форм, используя способность этого калькулятора быстро вычислять многие десятичные разряды и (точно и точно) преобразовывать непрерывные дроби в форму `(a \ pm sqrt (b)) / c`. Тогда мы можем найти математическое доказательство того, что наши результаты действительно верны.
Измените Точность работы на 50, 100 или даже 200 dps, чтобы увидеть, сохраняются ли шаблоны с большей вычислительной точностью.

Рекомендации

• 66.41 Некоторые тригонометрические отношения в форме Сурда Дж. М. Питерс Математическая газета Vol. 66 (1982), стр. 296-299
  хотя есть некоторые ошибки в его формулах с участием τ (наш Фи), которые исправляются в уравнениях на этой странице.

1996-2017 Доктор Рон Нотт
обновлено 30 мая 2017

Похожие

Комментарии