Слово « иль » - это вопросительное местоимение, хотя и не всегда, потому что оно может быть и указывает, например, сколько поляков имеет так много взглядов - поэтому, если вопросительного знака нет, вам нужно угадать, что спрашивает автор: спрашивает он или утверждает. :-)
Понятие действительного числа является существительным и определяет набор, содержащий числа с характерными свойствами, которые отличают этот набор от других наборов, при этом один элемент этого набора обладает свойством, которое он может быть обозначен как ТОЧКА на декартовой числовой оси. Википедия объясняет это так:
«Классическая модель (из набора действительных чисел) - это так называемая простая действительная или иным образом числовая ось , Форма действительных чисел тело "
Ссылка на слово «тело» применяется категория : Теория тел и предоставляет информацию, с которой, в частности, имеет дело совокупность функций, функций или областей функции Галуа, Римана , дедекиндово , Дирихле и немецкие математики, французские математики и американские алгебраисты, и где-то на заднем плане, реальные имена появляются на заднем плане при построении действительных чисел кантор коши и Тарский ,
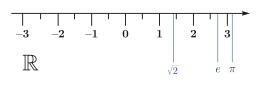
 Числовая ось как геометрическая интерпретация множества действительных чисел
Числовая ось как геометрическая интерпретация множества действительных чисел
Что может извлечь из этого обычный едок хлеба, такой как я? Ну, я могу нарисовать это:
- действительные числа - это такие точки на числовой линии, которых так много, что они образуют тело, и тело обладает этим свойством, что в нем нет отверстий, и, следовательно, независимо от того, какой отрезок этой оси будет сделан, пересечение будет действительным числом, и нет вероятность того, что ось с линией реза не имеет общей точки,
- на числовой оси есть все точки, образующие набор действительных чисел ℛ, и ни одна из них не пропущена, поэтому нет возможности установить точку, которой раньше не было бы,
- точки вне числовой оси не являются частью набора действительных чисел ℛ.
Из пункта 1 следует, что точка, являющаяся действительным числом на числовой оси, должна иметь контакт (контакт, контакт, касание, граница, связь) с соседними точками (предшественник и преемник), поскольку, если бы этого отношения не было, действительные числа не были бы согласованными и они не сделали бы тело.
Из пункта 2 следует, что множество действительных чисел ℛ является ПОЛНЫМ множеством и, следовательно, имеет фиксированное число элементов, которые его создают, поскольку, поскольку все точки отсутствуют, и ни одна из них не пропущена, это число является инвариантным и является арифметическим числом.
Из пункта 3 следует, что множество ℛ не является наибольшим множеством, поскольку оно не содержит всех элементов. Точки вне числовой оси создают множества, большие ℛ и относительно ℛ являются комплексными числами (числами из другого измерения).
Каждая точка, которая является действительным числом, должна иметь свое ИМЯ, чтобы отличаться от других точек, и это имя встречается только ОДИН раз во всем наборе. По имени (после упрощения до простейшей формы) действительные числа можно классифицировать на:
- положительные и отрицательные целые числа (например, a; b)
- фракции, представляющие собой отношение двух целых чисел a / b (например, 3,23, 7/15)
- не поддающиеся количественному определению числа, то есть те, которые не могут быть записаны как дробные а / б (например, √2, π, ln5, sin22)
Проще всего из набора действительных чисел ℛ отделить подмножество натуральных чисел, которые с начала дня имеют название: натуральные числа, а множество было названо ℕ. Этот набор на числовой оси начинается с номера ONE, потому что ONE - это имя первого сегмента (нет раздела ZERO), а последующие числа из набора +1 на +1 больше, чем предшественник. ОДИН номер - это первое натуральное число на числовой оси, независимо от того, в какой системе записи эта ось описана. В западной цивилизации десятичная система используется сегодня.
Так же, как набор действительных чисел ℛ является полным набором и имеет фиксированное число элементов, создающих его, так и это арифметическое число - так же и его подмножество ℕ является полным набором, в котором отсутствует имя, созданное алгоритмом n + 1, и последнее число в этом наборе граница множества называется бесконечностью, хотя множество конечно и символ nad был задан этой бесконечности. Также предполагалось, что элементы szereg бесконечны в разрядах, в частности, существует так много десятичных знаков.
С помощью этих данных можно подсчитать, сколько действительных чисел записано в числовой оси, но ранее исторический вклад. Первым человеком в современной истории, который обнаружил, что есть коллекции, более многочисленные, чем натуральные числа бесконечности ∞, был Георг Кантор (1845 - 1918), который показал, что действительные числа в диапазоне от нуля до единицы больше бесконечности ∞. Он назвал это число континуумом с символом ℂ. Рассуждения Кантора были просты: поскольку набор степеней 2 ^ n> n равен 2 ^ ∞> ∞ и показал это с помощью диагонального метода, который он задумал.
И сколько именно действительных чисел находится в этом диапазоне [0, 1]? В десятичной системе записи их ровно 10 ^ ∞, поэтому ℂ в десятичной системе записи больше, чем набор мощности Кантора. A равно 2 ^ ∞ в двоичной системе записи.
Похожие
Умножение двух чиселСлово умножение происходит от латинского слова «multiplicare» и означает «умножение». Таким образом, вы умножаете один номер к другому. ваш результат в конце счета так больше чем первый номер. Таким образом, вы можете проверить, Как обезопасить свой BIOS
Вероятно, вы не сильно взаимодействуете с BIOS вашего ПК (Базовая операционная система ввода / вывода), но он занимает уникальную и очень привилегированную позицию в архитектуре вашего компьютера. Поскольку BIOS загружается до того, как операционная система - и до того, как вы введете свои учетные данные пользователя, Как украсить современные интерьеры?
Функциональность и простота современного стиля соблазняет многих владельцев квартир. Однако каждый, кто хочет украсить интерьеры в едином модернистском стиле, должен знать, что обработка деталей и правильный подбор добавок занимает некоторое время, требует некоторой подготовки одновременно. Неослабная популярность современного стиля состоит из многих факторов. Модернистски меблированные квартиры в первую очередь характеризуются широкой функциональностью. Как ваше лицо стареет?
... как на улучшение эстетических, так и на оздоровительных функций кожи, - подчеркивает д-р Василевская. Один из вариантов - пройти процедуру, которая улучшит способность стимулировать выработку коллагена в тканях. Это, среди прочего, Sculptra ™, который естественным образом стимулирует кожу восстанавливать утраченный объем и эластичность. Продукт восстанавливает молодую форму щек, заполняет носогубные складки, наносится в непосредственной близости от так называемых «Хомяки» Как образовалась планета Земля?
Человеку всегда было интересно знать, как и когда образовалась Земля, планета на которой он живет. На эту тему существует много научных гипотез и простых предположений. Гипотез о происхождении нашей планеты значительно больше, чем гипотез о происхождении Вселенной. В данной статье рассмотрим некоторые теории относительно появления Земли. Как образовалась Как организовать причастный прием дома?
Подсчитано, что на подготовку Первого Причастия многие родители тратят столько же, сколько на организацию ... свадьбы , На самом деле, когда вы учитываете все расходы - покупка платьев, подарков, аренда ресторанов и других дополнительных развлечений , сумма становится Как украсить очень маленькую ванную
1. Большое зеркало Иногда хочется переместить стены в небольшой интерьер? ;) Я тоже, но, к счастью, есть более простые и более быстрые способы увеличить немного меньше. По крайней мере, оптически, и это что-то, верно? Маленькая ванная проверит зеркало, которое мы до сих пор вешаем в нем. С одной стороны, рама не должна быть огромной, чтобы не нарушать пропорции комнаты. Но с другой стороны, если вам небезразлично ощущение свободы и расслабленности в слишком маленькой ванной Как стать хорошим главным бухгалтером?
Каждый человек стремится к своей цели, испытывая огромное желание добиться в профессиональной сфере высокой отметки. Не важно какую профессию он выбрал, главное профессионализм. Почти каждый счетчик, Во сколько родителям обойдется первоклассник
... какая сумма нужна для того, чтобы подготовить ребенка к первому сентября», - отметили в аналитическом центре. Чтобы собрать первоклассника в школу, родителям нужно от 534 до 974 грн, общая сумма будет зависеть от качества приобретенных вещей. В набор включили только самое необходимое: школьную форму, брюки и две рубашки для мальчика, форму, сарафан и две блузки для девочки, пару туфель, одежда и обувь для занятий физкультурой, рюкзак, базовое канцелярские принадлежности и тетради. Как собрать шкаф своими руками
как собрать шкаф своими руками После покупки корпусной мебели многих интересует, как теперь все это собрать. И действительно у человека, который не имеет какого-либо опыта в Как кровать изменит вашу спальню?
Одиночные, двухместные, деревянные, металлические, детские и взрослые - мы любим всех! В конце концов, именно на них, на всевозможных кроватях, можно свободно ложиться после утомительного дня, отдыхать и отправляться в путешествие, полное сонных приключений! Но ... так как все прекрасно, как выбрать лучшее? Удача по утрам, отсутствие болей в позвоночнике, удовольствие спать и вставать каждый день - это простые мечты, которых, к счастью,
Комментарии
Есть много статей из Википедии, но сколько на самом деле есть видео?Есть много статей из Википедии, но сколько на самом деле есть видео? 4.18 ТВОРЧЕСКИЕ ВИДЕО ИДЕИ YOUTUBE • философские видео Сделайте видео по философии Возьми своего зрителя вниз по философской кроличьей норе вашей темы. Это еще один способ добавить контекст к тому, что вы исследовали в Но как это на самом деле и мы должны бояться?
Но как это на самом деле и мы должны бояться? Первое - это вредность бензола. На самом деле, вещество здесь токсичный, канцерогенный и повреждающий костный мозг , Но насколько правдив тот факт, что бензин выделяется из горячего пластика в автомобиле и выбрасывается вместе с воздухом из автомобильной системы кондиционирования воздуха? Нет тестов, подтверждающих такую угрозу, но Но как насчет ребенка, который не спит так, как ожидалось, и как насчет его матери?
Но как насчет ребенка, который не спит так, как ожидалось, и как насчет его матери? Разочарование, гнев и чувство вины могут сочетаться, чтобы заставить мать чувствовать себя обиженной на кого-либо еще, включая ее партнера, который может хорошо выспаться ночью. Она также может начать обижаться на своего ребенка. И все же бодрствование - абсолютно нормальный механизм выживания, запрограммированный на детей, чтобы они получали достаточно пищи для роста. Сон и бодрствующие дети всегда Как развиваются бинарные системы с этими объектами и как часто они сталкиваются?
Как развиваются бинарные системы с этими объектами и как часто они сталкиваются? Являются ли эти системы источником наблюдаемых, но таинственных коротких гамма-всплесков, которые мы часто видим? (LIGO уже внесла свой вклад в ответ на этот вопрос! Наше обнаружение сталкивающихся нейтронных звезд в августе 2017 года предоставило четкие доказательства того, что, по крайней мере, некоторые короткие гамма-всплески, на самом деле, вызваны сталкивающимися нейтронными звездами.) Насколько И он, клиент, знает ли он, что он на самом деле ест?
И он, клиент, знает ли он, что он на самом деле ест? Это проблема, которая иногда беспокоит меня, когда я должен есть вне дома, когда я выбираю продукты в супермаркете или на рынке. Иногда неизбежно просто уйти в отставку или поверить. Но во что я верю? Я верю, что что бы я ни делал, куда бы я ни шел, что бы я ни ел, это лучше для По пути назад к Тинчи вы вошли после того, как дель пауза вызвала раненых, как вы попали в Нью-Йорк?
По пути назад к Тинчи вы вошли после того, как дель пауза вызвала раненых, как вы попали в Нью-Йорк? Мне было очень приятно всегда быть лучше от собаки. Пауза была долгой, у меня чуть медленнее в спине, но я первый, предварительный мм мм подряд. Это будет лучше. Градец м это прекрасное время там. Было ли это против педа уткнм урит экстрасенсорной подгонки? Я думаю, что это было легко, особенно domc, и что podailo, чтобы поймать аресты, что должно начаться. Как устроены часы и как они работают?
Как устроены часы и как они работают? Высота около 1,5 м, корпус - стеклянный вакуумный рукав. Счетчик, или циферблат, стоит рядом с витриной, и это обычный экран дисплея компьютера. Внутри стеклянной трубки на стержне из стали и никелевого сплава, который, по меньшей мере, претерпевает температурные изменения, висит вес 10 кг. Внутри тройного стеклянного шкафа температура поддерживается с точностью до одной десятой градуса, а в трубе - давление одной десятой паскаля, то есть 10000. раз В английском мы часто встречаем слова «один, один, другой и другой» - что они на самом деле и когда их следует использовать?
В английском мы часто встречаем слова «один, один, другой и другой» - что они на самом деле и когда их следует использовать? Специально для вас мы подготовили статью, в которой вы узнаете все о них. В английском есть слова, которые могут иметь несколько значений. Хорошим И будет цена такой же, как сейчас, это большой вопрос, потому что на сколько еще снизят?
И будет цена такой же, как сейчас, это большой вопрос, потому что на сколько еще снизят? Это влечет другой вопрос: а куда направлять газ собственной добычи? А ответ прост: промышленности. То есть собственный газ получать промышленность. Заявленная схема, когда речь идет о снижении цены для определенной категории потребителей, выглядит довольно странно. Разумеется, когда контрактом вычитаются ценовые паритеты, это логично, но когда международному контракту начинают высчитывать Сколько вы можете сэкономить и как работает наш страховой калькулятор?
Сколько вы можете сэкономить и как работает наш страховой калькулятор? Благодаря движку сравнения страхования: Вы познакомитесь с конкурентными предложениями нескольких или десятка или около того обществ в одном месте сравнить и настроить страховку в соответствии с вашими потребностями вы выберете самый дорогой продукт вы сэкономите время, которое вам придется потратить Сколько это стоит и сколько стоит школьный план в 2017 году?
Сколько это стоит и сколько стоит школьный план в 2017 году? В ходе опроса, проведенного 18-21.08.2017 на портале AgroFoto.pl, мы спросили фермеров о потребностях, связанных с возвращением их детей в школу. Список расходов настолько велик, что некоторые из нас вынуждены брать кредиты. Циклический тест Провизионного барометра показывает, что в этом году средний поляк потратит около 530 злотых на одного ребенка . Чем мы отличаемся от фермеров?
И сколько именно действительных чисел находится в этом диапазоне [0, 1]?
Как ваше лицо стареет?
1. Большое зеркало Иногда хочется переместить стены в небольшой интерьер?
По крайней мере, оптически, и это что-то, верно?
Ак как все прекрасно, как выбрать лучшее?
Есть много статей из Википедии, но сколько на самом деле есть видео?
Но как это на самом деле и мы должны бояться?
Но как насчет ребенка, который не спит так, как ожидалось, и как насчет его матери?
Как развиваются бинарные системы с этими объектами и как часто они сталкиваются?
 МОЯ ТВОРЧЕСКАЯ ЛАБОРАТОРИЯ
МОЯ ТВОРЧЕСКАЯ ЛАБОРАТОРИЯ