Эти две сложности (нелинейность и негармоничность) деформируют   паутинообразную структуру и делают ее более запутанной. Как мы могли бы описать  такую деформацию?

   Во-первых, давайте рассмотрим негармоничность. Каждая периодическая вибрация (даже негармоничная) может быть выражена гармоническими компонентами Фурье. Уже существующие уравнения (по определению) линейны, таким образом, можно обнаружить отдельные решения для каждого гармонического компонента отдельно (как мы знаем, самые простые решения – киральные структуры в форме тороидальных узлов), затем, мы можем суммировать  эти решения для отдельных гармонических компонентов. Следовательно, совокупное решение должно быть суммой, представленной различными узлами (разное k' для  разных гармонических компонентов). Отношение между частотами гармоничных компонентов очень регулярно (отношение между разными числами), тогда уравнение (3)  (вместе с допущением линейности) тоже создает регулярное  отношение между параметрами k'. 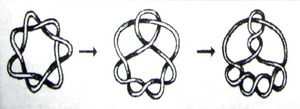Это означает, что структура совокупного узла (сочетание всех гармоничных компонентов) тоже будет регулярной. Естественно, совокупный узел теперь намного более запутанный, чем тороидальный, и, более того, его совокупная топология меняется в течение одного периода (чего не происходит с узлом одного чистого гармонического компонента).

   Но теперь, мы все еще имеем нелинейность функции (4). Это условие изменяет структуру узла еще более радикально. Чтобы упростить анализ, давайте начнем с паутины, состоящей из одного чистого гармонического компонента.

   Нелинейная зависимость (4) может быть записана в форме потенциального ряда степеней (но без условия, что n = 0, ибо когда В = 0, j = 0 тоже; нет синтропического направления частиц).

               j = ∑ р_n • Bⁿ                                                                          (8)

               n = 1,2,3…

   Давайте понаблюдаем за условиями, когда В увеличивается от В = 0. Сначала В маленькое (например, в тороидальном узле). В более высоких полях линейная структура страдает от непрерывной деформации. Позже, в критическом поле В_k создается неустойчивость, и узловая струк-тура страдает от резкого изменения (фазового превращения). При еще более высоком поле В, в дополнительную структурную разновидность вносится бифуркация. Хотя такие бифуркации тоже являются видом фазового превращения, они обладают особым свойством; из первоначальной фазы не всегда развивается такая же новая фаза – существует несколько возможностей. Линия фазовых возможностей расщепляется с каждой бифуркацией. Магнитный узел еще больше усложняется, хотя внутренне упорядочен не меньше (рисунок 4). Подобные явления известны из неравновесной термодинамики рассеивающихся систем (например, хорошо известные клетки Бенарда в турбулентной жидкости). Однако, существует и основное отличие: Синтропические структуры  не нуждаются в подпитке из окружения (например, в подпитке температурными различиями, как в случае клеток Бенарда, или посредством некоторых других градиентов).