Давайте на минуту прервемся: Граница между информационной паутиной и классическим фотоном четко не определена. На этих страницах описывается бездействующая информационная паутина, хотя она, также, может обладать компонентом скорости (и все же медленнее, чем скорость света). Чем больше ее скорость приближается к скорости света, тем больше она похожа на классический фотон.

   Следуя обычным процедурам с дифференциальными уравнениями Максвелла, мы легко можем найти циклическую частоту информационной паутины:

               k² = ε_оμ_о • ω², или более просто

               ω = ck                                                                                   (3)

   где с – скорость света в пустоте.

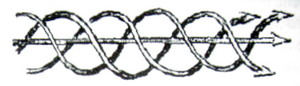
   Также, мы хотим определить пространственную конфигурацию этих решений. Нас интересует форма магнитных и электрических линий (обе имеют одинаковую форму). Существует много классов решений, но, сначала, мы будем ограничиваться такими решениями, которые проще всех и не слишком чувствительны к пограничным условиям. Как уже упоминалось, такие решения  должны демонстрировать фактор асимптоты. Такое поле можно визуализировать как прямую, бесконечно длинную веревку, составленную из торсионно закрученных линий поля (рис. 1)

   Закручивание в центре веревки похо-же на правостороннюю спираль, если k>0, и на левостороннюю спираль, ес-ли k<0. Но наблюдение пограничных условий говорит, что решение относи-тельно цилиндрической  системы ко-ординат не удовлетворительно. То есть, поле В не стремится к нулю, когда мы удаляемся в направлении z. Также, когда мы удаляемся в направлении r, оно не стремится к нулю достаточно быстро (результат потери асимптотического поведения). Полная магнитная энергия, которая может быть выражена пространственным интегралом ∫_v (2μ_о) • В² dV (интегрирование по всей области V), отклоняется, даже когда подсчитывается только магнитная энергия в веревке конечной длины.

   Обе эти проблемы могут быть решены с помощью слегка измененной полевой структуры. Давайте представим, что вышеописанная веревка в поле имеет конечную длину (тогда мы имеем сегмент веревки) и скручена в виде замкнутой петли (рис. 2). В этом случае мы можем сразу же избежать первой проблемы. А как насчет второй? Несмотря на то, что благодаря новой модификации, в середине веревки поле меняется незначительно, оно может значительно измениться в области, удаленной  от центра петли. Следовательно, можно ожидать абсолютно новых решений – возможно с конечной магнитной энергией.

   Когда уравнение (1) анализируется в тороидальной системе координат^, , могут быть найдены характеристики новых решений. Исчисления здесь очень сложные. Решения (тороидальные решения) не могут выражаться обычными аналитическими функциями. Но визуально, такие решения очень привлекательны. Они похожи на вышеупомянутые замкнутые петли, сделанные из спирально закрученных веревок. Таким образом, линии поля обладают той же самой структурой, что и нити тороидальных узлов. Тороидальные узлы можно визуализировать как нить, намотанную на поверхность тора. Самый простой тороидальный узел показан на рисунке 3 (см. следующую страницу).