Home › News

Чему равна абсолютная погрешность числа 2. Приближенные вычисления и оценка погрешностей

20.12.2018

Разность точного и приближенного значений величины называется погрешностью приближения ( обозначается х),

т.е. х=х- а - погрешность приближения

откуда х= а + х,

т.е. истинное значение равно сумме приближенного значения и погрешности приближения.

Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближенного значения числа х.

т.е. - абсолютная погрешность приближения.

Запись х= а h означает, что истинное значение величины х заключено между границами, т.е. а - h х а + h

Пример 1. На предприятии 1284рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 -1284 = 16. При округлении до 1280 абсолютная погрешность состав­ляет 1284 - 1280 = 4.

Пример 2. Даны приближенные значения числа х= ; Какое из этих трех приближений является лучшим?

Решение:

Находим ; Лучшим приближением числа х является

Пример 3. Длина детали х (см) заключена в границах 33 х 34. Найти границу абсолютной погрешности измерения детали.

Решение: Примем за приближенное значение длины детали среднее арифметическое границ: а=(33+34)/2 = 33,5 (см).

Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см). Величину можно найти и как полуразность верхней и нижней границ, т.е. = (34-33)/2 = 0,5 (см). Длина детали х , найденная с точностью до =0,5 (см), заключена между приближенными значениями числа х :

33,5-0,5 х 33,5+0,5;

х=33,5 0,5 (см).

Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения и обозначается .

Является относительной погрешностью приближения

Пример 1. При измерении длины L и диаметра проводника получили L =(10,0 0,1) м , d = (2,5 0,1) мм. Какое из этих измерений точнее?

Решение: Измерение длины проводника производилось с точностью до 0,1м=100мм, а измерение диаметра проводника – с точностью до 0,1мм.

При измерении длины проводника допускается абсолютная погрешность в 100мм на 10000мм, и, следовательно, допустимая абсолютная погрешность составляет

Измеряемой величины.

При измерении диаметра допустимая абсолютная погрешность составляет

Измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.

Пример 2. Известно, что 0,111 является приближенным значением для Найти абсолютную и относительную погрешности этого приближения.

Решение: Здесь х= , а =0,111. Тогда = х- а = 1/9 – 0,111 = 1/9000-а.п.п,

Пример 3. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-197 = 3. Относительная погрешность равна или, округленно, %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относи­тельная) не превосходит некоторого числа.

Пример 4.

Продавец взвешивает арбуз на ча­шечных весах. В наборе гирь наименьшая- 50 г. Взвешивание дало 3600 г. Это число - приближенное. Точная масса арбуза неизвестна. Но абсолютная по­грешность не превышает 50 г. Относительная погреш­ность не превосходит %.

Комплексные числа.

Графическое изображение комплексных чисел. Изображение комплексных чисел.

Комплексные числа записываются в виде: a+ bi . Здесь a и b – действительные числа , а i – мнимая единица, т.e. i 2 = –1.Число a называется абсциссой , a b – ординатой комплексного числа a+ bi. Комплексное число 0 + bi называется чисто мнимым числом .Запись bi означает то же самое, что и 0 + bi .

Модулем комплексного числа называется длина вектора OP , изображающего комплексное число на координатной ( комплексной ) плоскости. Сопряжённые комплексные числа имеют одинаковый модуль

Рассмотрим на плоскости декартову прямоугольную систему координат xOy . Каждому комплексному числу z = a + bi можно сопоставить точку с координатами (a;b) , и наоборот, каждой точке с координатами (c;d) можно сопоставить комплексное число w = c + di . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

Пример. Изобразим на комплексной плоскости числа

Z 1 = 2 + i; z 2 = 3i; z 3 = -3 + 2i; z 4 = -1 – i.

Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу ( a + bi ) ± ( c + di ) = ( a ± c ) + ( b ± d ) i , а умножение - по правилу ( a + bi ) · ( c + di ) = ( ac – bd ) + ( ad + bc ) i (здесь как раз используется, что i 2 = –1). Число = a – bi называется комплексно-сопряженным к z = a + bi . Равенство z · = a 2 + b 2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

Например,

Задачи для самостоятельного решения

Раздел 1. Приближенные числа и действия над ними

1.1 Виды погрешностей при приближенных вычислениях

Точное решение некоторых математических задач невозможно получить классическими методами, или это решение может быть получено в таком сложном виде, что неприемлемо для дальнейшего практического использования. Кроме того, точное решение задачи может потребовать очень большого количества (от нескольких десятков до многих миллиардов) действий. В таких случаях прибегают к приближенным и численным методам решения.

Появление компьютеров значительно расширило область применения этих методов. В настоящее время трудно себе представить инженера, не владеющего компьютером и методами приближённых вычислений.

Заметим, что любой компьютер способен запоминать большие, но конечные массивы чисел и производить над ними арифметические операции и сравнения с большой, но конечной скоростью. То есть машина способна выполнять очень большое, но конечное число операций. Поэтому при работе на компьютере можно использовать только те математические модели, которые описываются конечным набором чисел, и использовать только конечные последовательности арифметических действий.

Математическими моделями различных явлений служат функции, производные, интегралы, дифференциальные уравнения и т.п. При работе на компьютере эти исходные модели следует заменить такими, которые описываются конечными наборами чисел с указанием конечной последовательности действий для их обработки. Для этого функцию заменяют таблицей, определённый интеграл — суммой и т.д. Кроме того, вычислительная машина обладает конечной памятью и может оперировать с числами конечной длины, поэтому промежуточные результаты округляются. В результате этого даже точный метод с конечным числом действий становится приближенным.

Таким образом, решение, полученное численным методом, является приближенным.

Причинами появления погрешностей являются:

Несоответствие математической модели изучаемому реальному явлению Погрешность исходных данных. Погрешность метода решения. Погрешности округлений в арифметических и других действиях над числами.

Погрешность решения, вызванная первыми двумя причинами, называется неустранимой — она не зависит от математика.

Погрешность метода возникает потому, что численным методом, как правило, решается не исходная задача, а более простая. Кроме того, обычно численный метод основан на бесконечном процессе, который приходится обрывать на некотором шаге.

Большинство численных методов зависит от одного или от нескольких параметров. Выбор параметров метода позволяет регулировать погрешность метода.

Погрешность округлений не должна быть существенно больше погрешности метода. А погрешность метода целесообразно выбирать в 2-5 раз меньше неустранимой погрешности.

1.2 Приближенные числа

На практике часто приходится иметь дело с числами, которые выражают истинную величину не точно, а приблизительно. Такие числа называются приближенными .

Обозначим точное числовое значение некоторой величины a , приближённое числовое значение этой же величины a * . Тогда a » a * .

Заменяя точное число a приближенным числом a * , мы совершаем ошибку (погрешность).

Определение 1.1. Абсолютной погрешностью приближенного числа a * называется абсолютная величина разности между этим числом и его точным значением | a - a * | .

Поскольку точное значение величины обычно бывает неизвестно, то невозможно вычислить и абсолютную погрешность. Но можно указать положительное число D (a *) , удовлетворяющее неравенству:

Любое число d (a *) , удовлетворяющее неравенству

Заметим, что чисел, удовлетворяющих неравенствам (1.2) и (1.3) множество. Поэтому величина предельной погрешности является не вполне определённой.

На практике обычно берётся по возможности меньшее значение предельной погрешности. Для каждого приближенного числа обязательно определяется его предельная погрешность (абсолютная или относительная). Предельная абсолютная погрешность позволяет установить пределы, в которых лежит число a , т.е.

Предельная относительная погрешность характеризует точность вычислений или измерений.

Примеры.

1.2.1 . При решении задач вместо точного числа p = 3,14159265... мы используем его приближенное значение 3,14 и совершаем ошибку:

p - 3,14 > 0,00159265

1.2.2 . При измерении длины пути получен результат 25,2 км с точностью до 2м . Вычислить предельную абсолютную и предельную относительную погрешности.

Решение . В нашем случае предельная абсолютная погрешность равна D = 0,002 км, а предельная относительная погрешность

Аналогично, вычисляем

означает, что a * является приближенным значением числа a с абсолютной погрешностью D (a *) . Если же a * является приближенным значением числа a с относительной погрешностью d (a *), то пишут так:

1.4 Значащие цифры, верные и сомнительные цифры

На практике используются различные приёмы, позволяющие уже только по записи самого приближенного числа судить о его погрешности.

Запись приближенных чисел и абсолютных погрешностей подчиняется определённым правилам.

В десятичной записи числа значащей цифрой называется любая цифра не равная нулю. Нуль считается значащей цифрой, если он расположен между значащими цифрами или стоит правее всех значащих

Пример 1.3.1. Приближенное число 0,38 имеет 2 значащих цифры, 0,308 — три, 0,3080 — четыре, 0,00308 — три. Значащими цифрами являются подчёркнутые цифры.

Определение 1.3. Значащая цифра называется верной в широком смысле если абсолютная погрешность числа не превосходит одной единицы разряда, соответствующего этой цифре.

Значащая цифра называется верной в узком смысле если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

В противном случае цифра считается сомнительной .

Если приближенное число записывается без указания его абсолютной (предельной абсолютной) погрешности, то выписываются только его верные цифры. При этом верные нули на правом конце числа не отбрасывают. Числа 0,25 и 0,250 как приближенные различны. Если же мы пользуемся записями вида (1.4) или (1.5), то числа в правых частях этих равенств должны быть записаны с одинаковым количеством знаков после запятой.

Абсолютную или относительную погрешность принято записывать в виде числа, содержащего одну или две значащие цифры. При этом округление производится с избытком.

Может оказаться так, что у приближенного числа в его целой части значащих цифр больше, чем верных знаков. В этом случае используется запись в нормализованном виде a * = m ·10 n , при этом число m ≤ 1 должно содержать только верные цифры. В нормализованной записи число m называется мантисса , n — порядок числа

Заметим, что предельная абсолютная погрешность определяется числом десятичных знаков после запятой: чем меньше десятичных знаков после запятой, тем больше D (a *) .

Предельная относительная погрешность определяется числом значащих цифр: чем меньше значащих цифр, тем больше d (a *) .

1.5 Округление

Для записи приближенных чисел с верными цифрами применяется округление .

Точные числа также требуется округлить, если количество используемых разрядов ограничено.

Округлением (по дополнению) числа называется запись этого числа с меньшим количеством разрядов по следующему правилу: если первая отбрасываемая цифра больше или равна 5, то последнюю оставляемую цифру увеличивают на единицу. При округлении чисел возникает погрешность, которую также надо учитывать.

Погрешность округления по дополнению не превосходит по абсолютной величине половины единицы младшего оставляемого разряда. При вычислении результирующей погрешности, погрешность округления надо прибавлять к первоначальной абсолютной погрешности числа.

Пример 1.3.2. Число a * = 413287,51 имеет относительную погрешность d (a *) = 0,01 . Из (1.3) следует, что D (a *) = | a * | d (a *) .

Поэтому абсолютная погрешность данного числа равна 4133. Это означает, что четвёртый разряд числа a * уже может содержать ошибку. Следовательно, верными являются только первые две цифры числа. Тогда в нормализованном виде это число записывается так: a * = 0.41 ·10 6 .

Рассуждая аналогично, приближенное число b * = 0,0794 при d (b *) = 2% запишем в нормализованном виде b * = 0.8 ·10 - 1 .

Заметим, что здесь нам потребовалось округлить число.

При выполнении арифметических действий с приближенными числами возникают две взаимообратные задачи:

1. По известным погрешностям входных данных оценить погрешность результата.

2. Определить точность исходных данных, обеспечивающую заданную точность результата.

Кроме того, при работе с приближенными числами необходимо согласовывать точность различных входных данных, чтобы не тратить время на выписывание ненужных и неверных цифр.

В процессе вычислений также необходимо следить за точностью промежуточных результатов.

До начала выполнения арифметических действий применяется округление, чтобы все числа, участвующие в этих действиях, были записаны с одинаковым количеством десятичных знаков. Количество оставляемых десятичных знаков определяется наименьшим числом верных цифр у исходных данных.

При сложении и вычитании приближенных чисел, имеющих одинаковое число верных цифр после запятой, округление не производится.

При сложении и вычитании приближенных чисел с различным числом верных цифр после запятой результат округляется по наименьшему числу верных цифр после запятой у исходных данных.

При умножении и делении приближенных чисел с различным числом верных цифр производится округление результата по минимальному числу верных цифр у исходных данных.

1.6 Погрешности арифметических операций

Пусть a * и b * - приближенные числа, тогда их сумма c * = a * + b * также является приближенным числом.

Если обозначить абсолютные погрешности слагаемых D (a *) и D (b *) , соответственно, то абсолютная погрешность числа c * определяется формулой

D (c *) = D (a *) + D (b *).

Следовательно, при сложении двух приближенных чисел их предельные абсолютные погрешности складывают.

Это правило справедливо для любого конечного числа слагаемых. Кроме того, формула (1.6) справедлива и для разности двух чисел.

Действительно, разность двух чисел можно представить в виде суммы

a * - b * = a * + ( - b *),

а абсолютная погрешность числа ( - b *) равна абсолютной погрешности числа b * .

Замечание При вычитании двух чисел одного знака относительная погрешность разности может оказаться значительно больше относительной погрешности каждого слагаемого. Особенно большая потеря точности происходит при вычитании близких между собой чисел.

Пример 1.4.1 . Пусть требуется найти разность 61,32 - 61,31 .

Абсолютные погрешности данных чисел, соответственно, равны D 1 = 0,01 и D 2 = 0,01. Найдём теперь относительные погрешности этих чисел:

При вычитании получится число 0,01 (замечаем, что произошла потеря трёх значащих цифр). Его абсолютная погрешность равна сумме абсолютных погрешностей слагаемых D 1 + D 2 = 0,02 .

Тогда относительная погрешность результата составляет

Сравнивая погрешности исходных данных и результата, обнаруживаем резкое возрастание относительной погрешности.

Из примера 1.4.1. следует, что надо стараться избегать вычитания близких по абсолютной величине чисел. Иногда этого можно добиться путём преобразования расчётной формулы. Если же невозможно избежать такого вычитания, то надо увеличить точность промежуточных вычислений с учётом потери значащих цифр.

При умножении и делении двух приближенных чисел a * и b * погрешности определяются по формулам:

D (a * b *) = | b * | D (a *) + | a * | D (b *),

d (a * b *) = d (a *) + d (b *),

(1.7)

D (a * / b * ) = | b * |D (a *) + | a * |D (b *) | b * | 2

d (a * / b *) = d (a *) + d (b *).

Таким образом, при умножении и делении приближенных чисел складывают их предельные относительные погрешности.

Замечание . Если абсолютная погрешность приближенного числа Δ (a *) не превышает единицы разряда, выраженного n -ой значащей цифрой в десятичной записи этого числа, для предельной относительной погрешности верно неравенство:

δ(a *) ≤ 1 / k 10 n - 1

где k - первая значащая цифра числа a * .

Если абсолютная погрешность приближенного числа D (a *) не превышает половины единицы разряда, выраженного n -ой значащей цифрой в десятичной записи этого числа, для предельной относительной погрешности верно неравенство:

δ(a *) ≤ 1 / 2 k 10 n − 1

где k - первая значащая цифра числа a * .

В последнем случае справедливо и обратное утверждение: если

d (a *) Ј 1/ 2 (k + 1)10 n - 1 ,

то тогда a * является приближенным числом, имеющим n верных знаков.

1.7 Погрешность функции

Пусть задана непрерывно дифференцируемая в области G функция

u = f (x 1 , x 2 , ј , x n).

Оценка погрешности приближенного вычисления значения функции заменяется оценкой модуля ее отклонения от точного значения, вызванное ошибками аргументов.

При этом отклонение функции заменяется ее полным дифференциалом, в котором прирашения аргументов заменяются их абсолютными погрешностями. Тогда предельная абсолютная погрешность значения функции определяется соотношением

Для предельной относительной погрешности имеет место равенство

При помощи формул (1.11), можно определить точность аргументов, обеспечивающую заданную точность значения функции.

Пример 1.5.1. Требуется измерить с точностью d = 1% площадь боковой поверхности усечённого конуса, радиусы оснований которого r 1 » 2м, r 2 » 1м , а образующая l » 5м .

С какой абсолютной погрешностью нужно измерить радиусы и образующую и со сколькими знаками, верными в широком смысле, нужно взять число p ?

Если D (a * ) не превышает единицы разряда, выраженного n -ой значащей цифрой, то a * называется числом, имеющим n верных знаков в широком смысле .)

Решение . Площадь боковой поверхности усечённого конуса вычисляется по формуле:

S = π l ( r 1 + r 2).

Таким образом, имеем функцию четырёх аргументов S = S ( p , l , r 1 , r 2) .

Найдём частные производные и разделим на S .

Из формул (1.11) выразим абсолютные погрешности аргументов:

следует, что число p следует взять с количеством знаков n = 3 .

ПРОВЕРЬТЕ СЕБЯ

Дано приближенное число a * = 1,0754327 и его предельная абсолютная погрешность D (a *) = 0,0005 .

Округлите это число, оставив верные цифры. Учтите погрешность округления.

Портняжной сантиметровой лентой измеряют длину окружности меридиана, пушечного ядра Царь-пушки и теннисного мяча. Измерение какой величины даст большую относительную погрешность?

При измерении радиуса круга с точностью до 0,5 см получилось число 12 см . Найдите абсолютную и относительную погрешности площади круга.

Выполните арифметические действия над приближенными числами, все цифры которых верны:

130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;

35,2 ·1,748;

Величиной называется то, что может быть в определенных единицах выражено числом. Например, длина, площадь, объем – это величины. Значение величины, в истинности которого мы не сомневаемся, называется точным (в дальнейшем х - точное число ). Но обычно на практике, отыскивая значение какой-либо величины, получают лишь ее приближенное значение (в дальнейшем а - приближенное число ). Например, при измерении физических величин с помощью измерительных приборов.

Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближения Предельной абсолютной погрешностью приближения или границей погрешности или оценкой абсолютной погрешности называется число 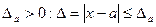. Таких оценок может быть бесконечное число. Лучшей оценкой погрешности является наименьшая оценка.

Краткая запись точного числа:

Отношение абсолютной погрешности приближения к модулю точного значения величины называется относительной погрешностью . На практике используется Для предельной относительной погрешности (оценки относительной погрешности): . Относительная погрешность обычно выражается в %.

В дальнейшем слово оценка опускается.

ПРИМЕР. Найти абсолютную и относительную погрешность приближения а=3,14 для х=π .

Известно, что 3,14 π.

Отсюда следует, что , т.е.

Если учесть, что 3,14 πто получим лучшую оценку

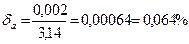
Цифра в десятичной записи приближенного значения величины х называется верной в широком смысле , если абсолютная погрешность приближения не превосходит единицы того разряда r , которому принадлежит эта цифра (Нулевым разрядом считается разряд единиц, десятичные цифры считаются отрицательными разрядами). Существует еще понятие верной цифры в узком смысле : . В дальнейшем будем рассматривать верные цифры в широком смысле. Остальные цифры числа называются сомнительными . Значащими цифрами числа, записанного в десятичной форме, называются все верные цифры числа, начиная с первой слева, отличной от 0. Все нули слева являются незначащими. По количеству значащих цифр можно легко оценить абсолютную погрешность приближенного числа. За оценку абсолютной погрешности можно взять 0,5 разряда, следующего за последней значащей цифрой. Предельную относительную погрешность можно принять равной дроби, числитель которой 1, а знаменатель – удвоенное целое число, записанное при помощи всех значащих цифр данного числа.

ПРИМЕР. а=0,065;

ЗАДАЧА 1.1. Объем помещения V определен с предельной относительной погрешностью δ Сколько значащих цифр в V ?

ЗАДАЧА 1.2. Известно, что приближенное значение а имеет n значащих цифр. Оценить абсолютную и относительную погрешность.