So lösen Sie die Multiplikation mit einer dreistelligen Spalte. Multiplikation mit dem Balken. Multiplizieren Sie Rechner

1. Wann fangen Kinder an, Zahlen zu brechen?
2. Beispiele für das Multiplizieren einer mehrstelligen Zahl mit einer einstelligen Zahl
3. Division in Multiplikation
4. Multiplikation großer Zahlen
5. Beispiele für das Multiplizieren einer mehrstelligen Zahl mit einer zweistelligen Zahl
6. Beispiel: 46 multiplizieren mit 73
7. Label Nummer 1: Quadratische Zahlen in den 50er Jahren
8. Label 2: Multiplizieren Sie zwei Zahlen in den 90er Jahren
9. Multiplizieren Sie eine dreistellige Zahl mit einer zweistelligen.
10. Welche Fehler können beim Multiplizieren gemacht werden und wie man sie vermeidet
11. Multiplizieren Multiplizieren mit mehreren
12. Wir lesen die Antwort: 46 multipliziert mit 73 ergibt 3358
13. Komponenten für Multiplikationsaktionen
14. Beispiel Argumentation während der Aufnahme Multiplikation in einer Spalte
15. Welche Fehler beim Multiplizieren kann und wie man sie vermeidet
16. Regeln für andere Fälle von Multiplikation
17. Multiplikation in einer Spalte von zwei mehrwertigen positiven ganzen Zahlen
18. Wie man in einer Spalte multipliziert: Grundregeln
19. Beispiele für das Multiplizieren einer mehrstelligen Zahl mit einer einstelligen Zahl

Leute, lasst uns wiederholen, was eine einstellige, zweistellige und dreistellige Zahl ist.

Eine einzelne Zahl ist eine Zahl, für deren Eingabe ein Zeichen erforderlich ist.
Zum Beispiel: 1, 3, 5, 4, ...
Wahrscheinlich haben Sie bereits erraten, dass die Ziffern einzelne Ziffern sind, wenn sie als Zahl geschrieben werden. Sie bestehen aus Einheiten.

Eine zweistellige Zahl ist eine Zahl, für deren Eingabe zwei Zeichen erforderlich sind. Beispielsweise sind alle Zahlen von 10 bis 99 zweistellige Zahlen. Sie bestehen aus Dutzenden und Einheiten.

Wann fangen Kinder an, Zahlen zu brechen?

Die Trennung erfolgt in der Schlüsselstufe 1, damit die Kinder wissen, dass die zweistellige Zahl aus zehn und einsen besteht. Die Idee ist, dass das Kind die Pfeile zusammenfügt, um den Zahlen zu entsprechen. Dies sind zwei häufig verwendete Methoden zum Hinzufügen großer Zahlen.

Der Lehrer kann beginnen, den Kindern beizubringen, im dritten Jahr zweistellige und dreistellige Zahlen hinzuzufügen, indem er sie in Abschnitte aufteilt. Der Grund dafür ist, dass es Kindern hilft, geistig ein Vielfaches von zehn und ein Vielfaches von 100 zu addieren. Kinder im 3. Jahr sollten außerdem lernen, wie man mit Hilfe dreistelliger Zahlen addiert, damit Ihr Kind wahrscheinlich auf beide Methoden stößt.

Eine dreistellige Nummer ist eine Nummer, für die Sie drei Zeichen benötigen. Sie haben bereits vermutet, dass alle Zahlen von 100 bis 999 dreistellig sind. Sie enthalten Einheiten, Dutzende und Hunderte.
Jungs, beantworten Sie die Frage: Wie viele dreistellige Zahlen gibt es?

Beispiele für das Multiplizieren einer mehrstelligen Zahl mit einer einstelligen Zahl

Nehmen wir ein Beispiel, um herauszufinden, wie die Multiplikationsoperation durchgeführt wird. mehrstellige Nummer auf einstellige Zahl .

Denken Sie zunächst an die Multiplikationsregel mit Null und Eins.
Diese Regel lautet:
Nummer * 0 = 0
Nummer * 1 = Nummer

Division in Multiplikation

Kinder ab dem 3. Lebensjahr müssen sich ebenfalls vermehren zweistellige Zahlen durch eine einstellige Zahl. Ihnen wird zum Beispiel normalerweise diese Partition beigebracht. Sobald die Lehrer sehr zuversichtlich sind, dass das Kind das Vielfache von zehn und einhundert multiplizieren kann, können sie dem Kind häufig erlauben, zu einer schnelleren Spaltenmethode zu wechseln.

Ab dem 6. Lebensjahr sollten die Kinder anfangen zu rechnen. Zur Vereinfachung kann der Lehrer ihnen zeigen, wie man Dezimalzahlen teilt. Es liest sich wie vier mal sechs gleich vierundzwanzig oder nur vier mal sechs - vierundzwanzig. Multiplikationskenntnisse sind sehr wichtig. Wenn Sie eine schwache Multiplikation haben, sollten Sie versuchen, den Besitzstand des folgenden „Zeitplans“ zu erreichen.

Beispiele
5 * 0 = 0;
18 * 0 = 0;
4506 * 0 = 0
1 * 34 = 34;
2384 * 1 = 2384;
1 * 47586 = 47586

Für die Multiplikation von mehrwertigen Zahlen wird häufig die Methode der Multiplikation mit einer Spalte verwendet, die wir in unseren Beispielen verwenden werden.

Multiplizieren Sie eine mehrstellige Zahl mit einer anderen Zahl als 0 oder 1.
Betrachten Sie Beispiele.
Nehmen Sie die Nummern 348 und 4. Der Einfachheit halber schreiben wir sie in eine Spalte. Wir beginnen die Multiplikation mit der rechten Spalte und multiplizieren die Zahlen 4 und 8. Wir erhalten die Zahl 32. Die Zahl 2 wird streng unter den Zahlen 8 und 4 geschrieben. Und die Zahl 30 wird zur nächsten Ziffer (dem Rang eines Dutzends) übertragen. Bei der Übertragung einer Zahl auf eine höhere Ziffer, beispielsweise von Eins auf Zehn, verliert diese Zahl 0. 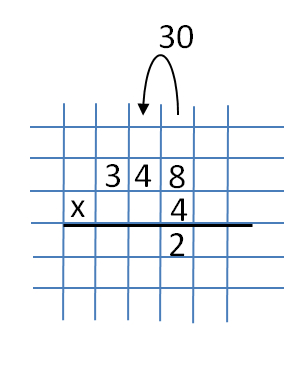Multiplizieren Sie nun 4 und 4 und erhalten Sie 16. Addieren Sie 3 aus der vorherigen Multiplikation. Als Ergebnis erhalten wir 19. Wir schreiben die Zahl 9 unter die Zahl 4 (links von der Zahl 2) und übersetzen 1 in die nächste Ziffer (die Entladung von Hunderten). Multiplizieren Sie dann die Zahlen 3 und 4 und addieren Sie 1 zum Ergebnis der vorherigen Aktion. Als Ergebnis erhalten wir 13. Wir schreiben es komplett auf, weil Dies ist unsere letzte Aktion. 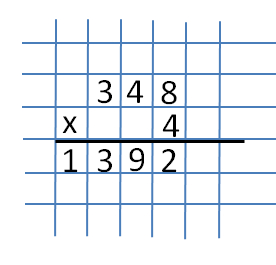Als Ergebnis erhalten wir das Produkt der Zahlen 348 mal 4, was 1392 entspricht.

Multiplikation großer Zahlen

Ihr Selbstvertrauen und Ihre Fähigkeit, Mathematik zu lernen, hängen weitgehend von Ihren Fortpflanzungskenntnissen ab. Deshalb sollten Sie sich bemühen, mit dem oben genannten „Zeitplan“ fertig zu werden.

• Das Produkt ist das Ergebnis der Multiplikation zweier Zahlen.
• Um 8 × 9 zu berechnen, rufen Sie die Tabelle acht Mal auf.

Um eine große Zahl mit einer anderen Zahl zu multiplizieren, können wir eine kurze oder lange Multiplikation verwenden.

Wenn Sie eine große Zahl mit einer einstelligen Zahl multiplizieren möchten, geben Sie die Zahlen vertikal ein. Die größere Zahl wird dann mit einer kleineren Zahl multipliziert. Um 89 × 7 zu berechnen, stellen Sie ihn vertikal mit einer kleineren Zahl unter der größeren Zahl ein, wie unten gezeigt. Berechnen Sie nun 7 × 8 und addieren Sie 6, um den Text wie unten gezeigt zu erhalten.

Beispiele für das Multiplizieren einer mehrstelligen Zahl mit einer zweistelligen Zahl

In diesem Beispiel betrachten wir die Multiplikation einer dreistelligen Zahl mit einer zweistelligen. Nimm die Nummern 925 und 38.
Der gesamte Multiplikationsprozess ist in mehrere Teile unterteilt.
Der erste Teil ist die Multiplikation der Zahl 925 mit der Zahl 8. Der Einfachheit halber schreiben wir sie in eine Spalte.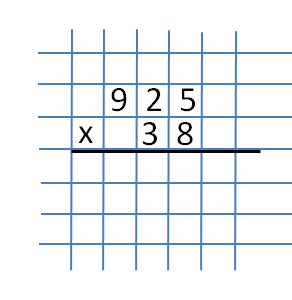
Wie üblich beginnen wir beim Multiplizieren in einer Spalte unsere Aktionen von der äußersten rechten Spalte aus. Dort werden die Zahlen 5 und 8 geschrieben und multipliziert, wodurch wir die Zahl 40 erhalten. Wir schreiben die Zahl 0 unter die Zahlen 5 und 8. Vergessen Sie nicht, 40 auf die nächste Stufe (Zehnerstufe) zu übertragen. 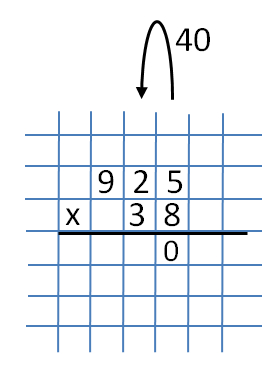Multiplizieren Sie nun die Zahlen 2 und 8. Wir erhalten 16. Vergessen Sie nicht, die Zahl 4 zu addieren, die nach der vorherigen Aktion verbleibt (wenn Sie 8 und 5 multiplizieren). Wir erhalten die Nummer 20. Die Nummer 0 wird unter die Nummer 3 neben der vorherigen Nummer 0 geschrieben, und 20 wird zur nächsten Ziffer (dem Rang von Hunderten) übertragen. Und die letzte Aktion des ersten Teils ist die Multiplikation der Zahlen 9 und 8. Das Produkt dieser Zahlen ist 72. Addieren Sie zum Produkt die Zahl 2 und wir erhalten die Zahl 74. Wir schreiben sie vollständig auf.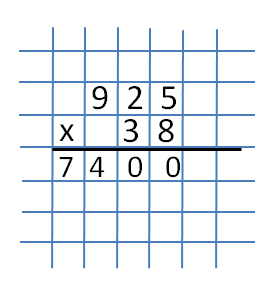
Der zweite Teil ist die Multiplikation der Zahl 925 mit der Zahl 3. Wir werden diesen Teil nicht wie den vorherigen betrachten, sondern einfach das Ergebnis des Produkts dieser Zahlen schreiben. Bei der Aufzeichnung des Produkts aus den Zahlen des zweiten Teils ist zu beachten, dass die Aufzeichnung nicht ab der rechten Spalte, sondern mit einem Versatz von eins beginnen sollte. In unserem Beispiel muss die erste Zahl genau unter den Zahlen 2, 3,0 stehen. Siehe die Zeichnung.
Der dritte Teil ist die Summe der Zahlen. Dies ist die letzte Phase, in der wir die Summe aus der ersten Arbeit (7400) und der zweiten Arbeit (2775) erhalten müssen. Wir fassen zusammen und beachten dabei die Regeln, die beim Hinzufügen zum Takt angewendet werden. Die letzte Abbildung zeigt das Ergebnis der Multiplikation einer zweistelligen Zahl 38 mit einer dreistelligen Zahl 925.

Die wichtigste Regel, mit der wir beginnen, die Multiplikation in einer Spalte zu untersuchen:

Wir geben oft eine Lösung wie folgt an. Das Multiplizieren von 38 mit 60 ist schneller als das Multiplizieren von 60 mit 38, da 60 Null enthält. Die Multiplikation mit 385 mal 500 ist schneller als die Multiplikation mit 500 mal 385, da 500 zwei Nullen enthält. Zwei multiplizieren große zahlen Schreiben Sie die Zahlen vertikal, und die größere Zahl wird mit der kleineren Zahl multipliziert, die als Multiplikator bezeichnet wird. Wir verwenden die Zeittabelle, um das Produkt einer größeren Zahl mit jeder Ziffer im Multiplikator zu finden und die Ergebnisse zu addieren. Wenn sich die Multiplikationsziffer beispielsweise in einer Hunderterspalte befindet, fügen Sie zwei Nullen für die Zehner- und die Eine-Spalte hinzu.

• Platzieren Sie also 3 in der Einheitenspalte und tragen Sie 6.
• Berechnen Sie dann 7 × 8 und addieren Sie 6, um 62 zu erhalten.
• In der Einheitenspalte wird Null gesetzt.
• Dann berechnen wir 6 × 38, wie oben gezeigt.
• In der Spalte der Einheiten steht Null sowie eine Spalte von Zehn.
• Dann berechnen wir 5 × 385, wie oben gezeigt.
• Vergessen Sie nicht, für jeden Wert der Stelle nach der Multiplikationsziffer eine Null hinzuzufügen.
• Um 269 mit 78 zu multiplizieren, setze 78 darunter.
• Dann berechnen wir 8 × 269 und 70 × 269, wie oben gezeigt.

Dies ist als kommutatives Gesetz zur Multiplikation bekannt.

Beispiel: 46 multiplizieren mit 73

Unter der Nummer 46 schreiben wir die Nummer 73 nach der Regel:

Die Einheiten stehen unter den Einheiten und Dutzende unter den Zehnern.

1 Multiplizieren Sie beginnend mit Einheiten.

3 mit 6 multiplizieren. Es stellt sich heraus, 18.

• 18 Einheiten sind 1 Dutzend und 8 Einheiten.
• Wir schreiben 8 Einheiten unter die Einheiten, und 1 Dutzend wird gespeichert und zu den Zehnern addiert.

Jetzt 3 mit 4 Dutzend multiplizieren. Es stellt sich heraus, 12.

Label Nummer 1: Quadratische Zahlen in den 50er Jahren

Mit den Labels von Mike Bister kann jeder gut rechnen. Wenn die Zahl aus Schritt 2 kleiner als 10 ist, müssen Sie eine Null voranstellen.

Label 2: Multiplizieren Sie zwei Zahlen in den 90er Jahren

Wenn Sie zwei Zahlen in den 90er Jahren miteinander multiplizieren, gibt die Zahl in Klammern neben jeder Zahl an, von wie weit diese Zahl entfernt ist.

Multiplizieren Sie eine dreistellige Zahl mit einer zweistelligen.

Dies ist einer meiner Lieblingstricks, weil es einfach ist und jeden verblüfft, der es sieht. Bitten Sie jemanden, zwei Zahlen unter 10 auszuwählen und eine über die andere zu schreiben. Bitten Sie die Person, sie hinzuzufügen, und tragen Sie die Antwort direkt unter die beiden Zahlen ein. Bitten Sie die Person, die beiden unteren Zahlen in die Spalte einzufügen und die Summe so lange zu addieren, bis Sie nur noch zehn Zahlen haben. Fügen Sie dann die gesamte Spalte hinzu. Beispiel: Jemand wählt die Nummern 4 und 7 und schreibt 4 darüber. Die nächste Zahl in der Reihe ist, weil 4 7 = Dann, wenn die unteren beiden Zahlen in die Spalte eingefügt werden, ist die nächste Zahl 18, weil 7 11 = Er muss so lange weitermachen, bis er nur noch zehn Zahlen hat, und dann fügt er alle hinzu Spalte.

12 Dutzend und sogar 1, nur 13 Dutzend.

In diesem Beispiel gibt es keine Hunderte, daher schreiben wir sofort Hunderte anstelle von Hunderten.

138 ist die erste Teilarbeit.

2 multiplizieren Dutzende.

7 Dutzend multipliziert mit 6 Einheiten ergeben 42 Dutzend.

• 42 Dutzend sind 4 Hundert und 2 Dutzend.
• 2 Dutzend schreiben unter den Dutzenden. 4 merken und zu den Hunderten hinzufügen.

7 Dutzend multipliziert mit 4 Dutzend erhalten 28 Hunderte. 28 Hunderte und sogar 4 werden 32 Hunderte sein.

Die Spalte könnte ungefähr so ​​aussehen. Sie werden sich die Zahlen schnell ansehen und ihm mitteilen, dass alle zehn Zahlen hinzugefügt wurden. Alles, was Sie tun müssen, ist, sich 76 anzuschauen und Dutzende von Ziffern hinzuzufügen. 76 7 = Dann setzen Sie 76 auf ein Ende. Wenn eine Person zwei große Zahlen gewählt hat, z. B. 8 und 9, kann die siebte Zahl eine dreistellige Zahl sein. Die Spalte sieht dann so aus.

Welche Fehler können beim Multiplizieren gemacht werden und wie man sie vermeidet

Siebte Nummer in diesem Fall. Hier sehen wir uns an, wie man zweistellige Zahlen multipliziert. Zuerst benutzte er die Methode, die von Yakov Trakhtenberg als Direktmethode bezeichnet wurde, und die zweite Methode, die von der „Zwei-Finger-Methode“ abgeleitet wurde. Beide Methoden funktionieren für jede Kombination aus zweistelligen Zahlen.

• 32 Hunderte sind 3 Tausend und 2 Hunderte.
• Wir schreiben 2 Hunderte unter Hunderte, und wir werden uns an 3 Tausend erinnern und zu Tausenden addieren.

In diesem Beispiel gibt es keine Tausender, daher schreibe ich sofort 3 anstelle von Tausenden.

3220 ist das zweite unvollständige Produkt.

3 Falten Sie das erste und das zweite unvollständige Werk gemäß der Hinzufügungsregel zur Spalte.

138 plus 3220 wird 3358 sein.

Wenn Sie die Zahlen mit zwölf multiplizieren möchten, werfen Sie einen Blick darauf. Die direkte Methode wird selten in Schulen unterrichtet, ist aber seit Jahrhunderten bekannt. In der Schule wird Ihnen normalerweise beigebracht, das Ergebnis der Multiplikation jeder Ziffer eines Multiplikators mit aufzuzeichnen einzelne Zeile und dann die Gesamtsumme.

Multiplizieren Multiplizieren mit mehreren

Stattdessen schreiben Sie nur die Antwort. Dazu führen Sie bei jedem Schritt einige Berechnungen durch. Paare, die nichts bedeuten, werden ignoriert. Diese Paare werden externe und interne Paare genannt. Ein externes Paar verbindet immer eine einzelne Ziffer des Multiplikators mit der Ziffer, nach der wir jetzt suchen. Ein internes Paar verbindet immer Dutzende von Ziffern mit der Ziffer rechts von der Ziffer, an der wir im Multiplikator arbeiten.

Wir lesen die Antwort: 46 multipliziert mit 73 ergibt 3358

(Klicken Sie auf das Bild)

Komponenten für Multiplikationsaktionen

(Klicken Sie auf das Bild)

Beispiel Argumentation
während der Aufnahme
Multiplikation in einer Spalte

Periodischer Bruch

Diese Methode ist im Wesentlichen dieselbe wie in der vedischen Mathematik, wenn sie beim Multiplizieren zweistelliger Zahlen die "vertikale und transversale" Sutra verwendet. Der Stil der Gleichung ist der einzige wirkliche Unterschied. In der vedischen Mathematik wird die Gleichung wie unten gezeigt in zwei Zeilen geschrieben. Bei der direkten Methode stimmt die Gleichung mit der Antwort unter der Multiplikation überein.

Sie können ein direktes Multiplikationsvideo mit zweistelligen Multiplikatoren anzeigen oder die folgenden Beispiele lesen. Die Anzahl der führenden Nullen stimmt immer mit der Anzahl der Stellen im Multiplikator überein. Wenn Sie also mit zweistelligen Zahlen multiplizieren, addieren Sie immer zwei hohe Nullen. Folgendes: Wir multiplizieren zwei einzelne Ziffern miteinander.

Überprüfen Sie sorgfältig und bewerben Sie sich in Ihren Aktionen!

Welche Fehler beim Multiplizieren
kann und
wie man sie vermeidet

Schau genau hin

um keine fehler zu machen!

Regeln für andere Fälle von Multiplikation

Multiplizieren Sie in einer Spalte mit einer einzelnen Zahl

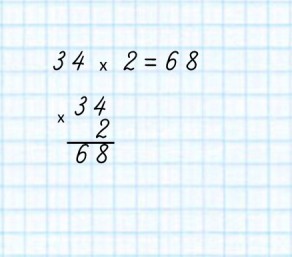
Dieser Schritt beinhaltet die Multiplikation von zehn Ziffern einer Zahl mit der Anzahl der Einheiten einer anderen. Wenn wir beim Schreiben einer Gleichung auf einer Linie gekrümmte Verbindungslinien zwischen multiplizierten Zahlen zeichnen, erhalten wir ein äußeres und ein inneres Paar. Wenn wir eine Gleichung auf zwei Linien schreiben, erhalten wir ein Kreuz, wenn wir gerade Verbindungslinien zwischen den multiplizierten Zahlen zeichnen.

Multiplikation in einer Spalte von zwei mehrwertigen positiven ganzen Zahlen

Addiert man die Ergebnisse dieser beiden Gleichungen, erhält man 14, schreibt also 4 und überträgt. In diesem Schritt multiplizieren wir zehn Ziffern jeder Zahl. Wenn Sie eine Gleichung in eine Zeile schreiben, wird das externe Paar in diesem Schritt mit Null verbunden, also das Ergebnis dieses Paares gleich null und kann ignoriert werden. In diesem Beispiel sind die mentalen Berechnungen, die wir durchführen müssen, relativ einfach. Da wir weniger Schritte als bei der herkömmlichen Multiplikationsmethode ausführen, ist dies schneller. Dieser Ansatz weist jedoch einen Nachteil auf, insbesondere wenn die beteiligten Zahlen größer sind.

Dieses Beispiel kann in eine Spalte geschrieben werden.

Unter der Nummer 34 schreiben wir die Nummer 2 nach der Regel:

Unter der Nummer 68 schreiben wir die Nummer 2 nach der Regel:

Wir multiplizieren zwei einzelne Ziffern miteinander. Also schreiben wir 2 und tragen. Hier wird es schwierig, insbesondere wenn Sie versuchen, eine Berechnung im Kopf durchzuführen. Also schreiben wir 4 und tragen. Wir haben 63, zu denen wir einen Carry 14 hinzufügen, um uns zu geben. Wir schreiben 7 und tragen.

Wie man in einer Spalte multipliziert: Grundregeln

Nach der ursprünglichen Methode und dem Grund für die führenden Nullen haben wir wegen der Übertragung einen zusätzlichen Schritt. Wir haben also Null plus eine Carry-7, die wir schreiben und die uns unsere Antwort gibt. Dieser Schritt mag überflüssig erscheinen und wir könnten die Übertragung im letzten Schritt notieren. Wenn Sie sich jedoch mit der Methode befassen, ist es besser, der gesamten Gleichung zu folgen, bis Sie mit der Methode vertraut sind, um kleine Etiketten zu erstellen.

Die Einheiten werden unter den Einheiten und Zehner geschrieben, wenn sie unter den Zehnern liegen.

1 Multiplizieren Sie beginnend mit Einheiten.

2 mal 8. Es stellt sich heraus, 16.

• 16 Einheiten sind 1 Dutzend und 6 Einheiten.
• 6 Einheiten schreiben wir unter die Einheiten. Und wir werden uns an 1 Dutzend erinnern und zu den Zehnen hinzufügen.

Jetzt 2 mit 6 Dutzend multiplizieren. Es stellt sich heraus, 12.

12 Dutzend und 1 weiteres nur 13 Dutzend.

Wie Sie sehen können, wird die Mathematik komplexer, wenn die Zahlen die Zahlen 7, 8 und 9 enthalten, insbesondere wenn Sie versuchen, dies mental zu tun. Jacob verstand dies auch und stellte sich die Aufgabe, einen einfacheren Weg zu finden, um dies zu erreichen. Geben Sie die so genannte Zwei-Finger-Methode ein, die die durchzuführenden Berechnungen vereinfacht. Bevor wir zur Zwei-Finger-Methode übergehen, müssen wir zusätzliche Referenzinformationen für die Ein-Bit-Multiplikation abrufen.

Beispiele für das Multiplizieren einer mehrstelligen Zahl mit einer einstelligen Zahl

Wenn Sie zwei Ziffern mit einer Ziffer multiplizieren, kann das Ergebnis nur aus einer oder zwei Ziffern bestehen. Wenn wir vor dem Ergebnis einer Ziffer eine Null setzen, können wir alle Ergebnisse der Multiplikation zweier Zahlen mit einer Ziffer in Form von zweistelligen Ergebnissen, Ziffern von Einheiten und Zehntel von Ziffern verarbeiten.

• 13 Dutzend ist einhundertdrei Dutzend mehr.
• 3 Dutzend schreiben unter den Dutzenden. Und wir werden uns an einhundert erinnern und zu den Hunderten hinzufügen.

In diesem Beispiel gibt es keine Hunderte, daher schreiben wir 1 sofort anstelle von Hunderten.

Wir lesen die Antwort : 68 multipliziert mit 2 wird 136 sein.