 МОЯ ТВОРЧЕСКАЯ ЛАБОРАТОРИЯ
МОЯ ТВОРЧЕСКАЯ ЛАБОРАТОРИЯ
|
|
06.09.2018
comp-science.narod.ru ==> Дидактические материалы по информатике ==> Системы счисления
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления . Если количество таких цифр равно P , то система счисления называется P -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию P системы счисления.
При переводе чисел из десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм:
1) если переводится целая часть числа, то она делится на P , после чего запоминается остаток от деления. Полученное частное вновь делится на P , остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на P , после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая дробь в системе счисления с основанием P . Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P .
1. Перевести данное число из десятичной системы счисления в двоичную:
а) 464(10); б) 380,1875(10); в) 115,94(10) (получить пять знаков после запятой в двоичном представлении).Решение.
464 | 0 380 | 0 |1875 115 | 1 |94 232 | 0 190 | 0 0|375 57 | 1 1|88 116 | 0 95 | 1 0|75 28 | 0 1|76 58 | 0 47 | 1 1|5 14 | 0 1|52 а) 29 | 1 б) 23 | 1 1|0 в) 7 | 1 1|04 14 | 0 11 | 1 3 | 1 0|08 7 | 1 5 | 1 1 | 1 0|16 3 | 1 2 | 0 1 | 1 1 | 1а) 464(10) = 111010000(2); б) 380,1875(10) = 101111100,0011(2); в) 115,94(10) » 1110011,11110(2) (в настоящем случае было получено шесть знаков после запятой, после чего результат был округлен).
Если необходимо перевести число из двоичной системы счисления в систему счисления, основанием которой является степень двойки, достаточно объединить цифры двоичного числа в группы по столько цифр, каков показатель степени, и использовать приведенный ниже алгоритм. Например, если перевод осуществляется в восьмеричную систему, то группы будут содержать три цифры (8 = 23). Итак, в целой части будем производить группировку справа налево, в дробной слева направо. Если в последней группе недостает цифр, дописываем нули: в целой части слева, в дробной справа. Затем каждая группа заменяется соответствующей цифрой новой системы. Соответствия приведены в таблицах.
| P | 2 | 00 | 01 | 10 | 11 |
| 4 | 0 | 1 | 2 | 3 |
| P | 2 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 8 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 2 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Переведем из двоичной системы в восьмеричную число 1111010101,11(2).
Переведем из двоичной системы в шестнадцатеричную число 1111010101,11(2).
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
При переводе чисел из системы счисления с основанием P в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и в дробной части, начиная с разряда сразу после запятой слева направо (начальный номер -1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления.
2. Перевести данное число в десятичную систему счисления.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 |
| -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| 0,5 | 0,25 | 0,125 | 0,0625 | 0,03125 | 0,015625 | 0,0078125 |
а) 1000001(2).
Замечание. Очевидно, что если в каком-либо разряде стоит нуль, то соответствующее слагаемое можно опускать.
б) 1000011111,0101(2).
| 0 | 1 | 2 | 3 | 4 |
| 1 | 8 | 64 | 512 | 4096 |
| -1 | -2 |
| 0,125 | 0,015625 |
в) 1216,04(8).
| 0 | 1 | 2 | 3 | 4 |
| 1 | 16 | 256 | 4096 | 65536 |
| -1 | -2 |
| 0,0625 | 0,00390625 |
г) 29A,5(16).
Для выполнения арифметических операций в системе счисления с основанием P необходимо иметь соответствующие таблицы сложения и умножения. Для P = 2, 8 и 16 таблицы представлены ниже.
|
|
|
|
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| A | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| B | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A |
| C | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B |
| D | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C |
| E | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D |
| F | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E |
| ´ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 2 | 0 | 2 | 4 | 6 | 8 | A | C | E | 10 | 12 | 14 | 16 | 18 | 1A | 1C | 1E |
| 3 | 0 | 3 | 6 | 9 | C | F | 12 | 15 | 18 | 1B | 1E | 21 | 24 | 27 | 2A | 2D |
| 4 | 0 | 4 | 8 | C | 10 | 14 | 18 | 1C | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C |
| 5 | 0 | 5 | A | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4B |
| 6 | 0 | 6 | C | 12 | 18 | 1E | 24 | 2A | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A |
| 7 | 0 | 7 | E | 15 | 1C | 23 | 2A | 31 | 38 | 3F | 46 | 4D | 54 | 5B | 62 | 69 |
| 8 | 0 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 58 | 60 | 68 | 70 | 78 |
| 9 | 0 | 9 | 12 | 1B | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 |
| A | 0 | A | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 |
| B | 0 | B | 16 | 21 | 2C | 37 | 42 | 4D | 58 | 63 | 6E | 79 | 84 | 8F | 9A | A5 |
| C | 0 | C | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 |
| D | 0 | D | 1A | 27 | 34 | 41 | 4E | 5B | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 |
| E | 0 | E | 1C | 2A | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 |
| F | 0 | F | 1E | 2D | 3C | 4B | 5A | 69 | 78 | 87 | 96 | A5 | B4 | C3 | D2 | E1 |
3. Сложить числа:
а) 10000000100(2) + 111000010(2) = 10111000110(2). б) 223,2(8) + 427,54(8) = 652,74(8). в) 3B3,6(16) + 38B,4(16) = 73E,A(16). 10000000100 223,2 3B3,6 + 111000010 + 427,54 +38B,4 ------------ ------- ----- 10111000110 652,74 73E,A
Выполним проверку результатов расчетов переводом в десятичную систему счисления. Для этого переведем каждое слагаемое и сумму в десятичную систему счисления, выполним сложение слагаемых в десятичной системе счисления. Результат должен совпасть с суммой.
а) 10000000100(2)=1 × 210+1 × 22 = 1024+4=1028(10)
111000010(2)=1 × 28+ 1 × 27+ 1 × 26+ 1 × 21 = 256+128+64+2 = 450(10)
10111000110(2)=1 × 210+ 1 × 28+ 1 × 27+ 1 × 26+ 1 × 22+ 1 × 21 = 1024+256+128+64+4+2 = 1478(10)
1028(10)+450(10) = 1478(10)
Результаты совпадают, следовательно, вычисления в двоичной системе счисления выполнены верно!
б) 223,2(8)=2 × 82+ 2 × 81+ 3 × 80+ 2 × 8-1 = 128+16+3+0,25 = 147,25(10)
427,54(8)= 4 × 82+ 2 × 81+ 7 × 80+ 5 × 8-1+ 4 × 8-2 = 256+16+7+0,625+0,0625 = 279,6875(10)
652,74(8)= 6 × 82+ 5 × 81+ 2 × 80+ 7 × 8-1+ 4 × 8-2 = 384+40+2+0,875+0,0625 = 426,9375(10)
147,25(10)+279,6875(10) = 426,9375(10)
Результаты совпадают, следовательно, вычисления в восьмеричной системе счисления выполнены верно!
в) 3B3,6(16)= 3 × 162+ 11 × 161+ 3 × 160+ 6 × 16-1 = 768+176+3+0,375 = 947,375(10)
38B,4(16)= 3 × 162+ 8 × 161+ 11 × 160+ 4 × 16-1 = 768+128+11+0,25 = 907,25(10)
73E,A(16)= 7 × 82+ 3 × 81+ 14 × 80+ 10 × 8-1 = 1792+48+14+0,625 = 1854,625(10)
947,375(10)+907,25(10) = 1854,625(10)
Результаты совпадают, следовательно, вычисления в шестнадцатеричной системе счисления выполнены верно!
4. Выполнить вычитание:
а) 1100000011,011(2) - 101010111,1(2) = 110101011,111(2). б) 1510,2(8) - 1230,54(8) = 257,44(8). в) 27D,D8(16) - 191,2(16) = EC,B8(16). 1100000011,011 1510,2 27D,D8 - 101010111,1 -1230,54 -191,2 -------------- ------- ------ 110101011,111 257,44 EC,B85. Выполнить умножение:
а) 100111(2) ´ 1000111(2) = 101011010001(2). б) 1170,64(8) ´ 46,3(8) = 57334,134(8). в) 61,A(16) ´ 40,D(16) = 18B7,52(16). 100111 1170,64 61,A *1000111 * 46,3 *40,D ------------- -------------- ---------- 100111 355 234 4F 52 + 100111 + 7324 70 + 1868 100111 47432 0 ---------- 100111 ------------- 18B7,52 ------------- 57334,134 1010110100016. Выполнить деление:
а) 100110010011000(2) : 101011(2)=111001000(2); б) 46230(8) : 53(8)=710(8); в) 4C98(16) : 2B(16)=1C8(16).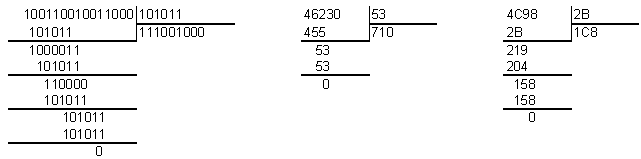
Калькулятор для работы в системах счисления с основаниями 2-36
История систем счисления
Представление числовой информации в памяти ЭВМ
Задачи по позиционным системам счисления
Дать определение системы счисления. Назвать и охарактеризовать свойства системы счисления. Какие символы используются для записи чисел в двоичной системе счисления, восьмеричной, шестнадцатеричной? Чему равны веса разрядов слева от точки, разделяющей целую и дробную часть, в двоичной системе счисления (восьмеричной, шестнадцатеричной)? Чему равны веса разрядов справа от точки, разделяющей целую и дробную часть, в двоичной системе счисления (восьмеричной, шестнадцатеричной)? Преобразуйте следующие десятичные числа в двоичные (восьмеричные, шестнадцатеричные): 0, 1, 18, 25, 128. Дешифруйте следующие двоичные числа, преобразовав их в десятичные: 0010, 1011, 11101, 0111, 0101. Дешифруйте следующие восьмеричные числа, преобразовав их в десятичные: 777, 375, 111, 1015. Дешифруйте следующие шестнадцатеричные числа, преобразовав их в десятичные: 15, A6, 1F5, 63.
© А.П. Шестаков , 1999-2009 Сайт создан в системе uCoz
|
© Беляев М.И., "МИЛОГИЯ"
Сайт ЯВЛЯЕТСЯ ТВОРЧЕСКОЙ МАСТЕРСКОЙ АВТОРА, открытой для всех посетителей. Убедительная просьба сообщать о всех замеченных ошибках, некорректных формулировках. Книги " Основы милогии ", " Милогия " могут быть высланы в Ваш адрес наложенным платежом, e-mail: [email protected] |