Jak rozwiązać mnożenie za pomocą trzycyfrowej kolumny. Mnożenie przez pasek. Pomnóż kalkulator

1. Kiedy dzieci zaczynają łamać liczby?
2. Przykłady mnożenia liczby wielocyfrowej przez liczbę jednocyfrową
3. Podział w mnożeniu
4. Mnożenie dużych liczb
5. Przykłady mnożenia liczby wielocyfrowej przez liczbę dwucyfrową
6. Przykład: 46 pomnóż przez 73
7. Etykieta numer 1: Kwadratowe liczby w latach 50-tych
8. Etykieta 2: pomnożenie dwóch liczb w latach 90-tych razem
9. Pomnożyć liczbę trzycyfrową przez liczbę dwucyfrową.
10. Jakie błędy można popełnić podczas mnożenia i jak ich unikać
11. Pomnóż przez pomnożenie
12. Przeczytaliśmy odpowiedź: 46 pomnożone przez 73 wyniesie 3358
13. Składniki akcji mnożenia
14. Przykładowe rozumowanie podczas nagrywania mnożenie w kolumnie
15. Jakie błędy podczas mnożenia może zrobić i jak ich uniknąć
16. Zasady dotyczące innych przypadków mnożenia
17. Mnożenie w kolumnie dwóch dodatnich liczb całkowitych o wielu wartościach
18. Jak pomnożyć w kolumnie: podstawowe zasady
19. Przykłady mnożenia liczby wielocyfrowej przez liczbę jednocyfrową

Chłopaki, powtórzmy, co jest jednocyfrową, dwucyfrową i trzycyfrową liczbą.

Pojedyncza liczba to liczba, która wymaga napisania jednej postaci.
Na przykład: 1, 3, 5, 4, ...
Prawdopodobnie już się domyśliłeś, że cyfry są pojedynczymi cyframi, gdy są zapisane jako liczba. Składają się z jednostek.

Dwucyfrowa liczba to liczba wymagająca do napisania dwóch znaków. Na przykład wszystkie liczby od 10 do 99 są liczbami dwucyfrowymi. Składają się z kilkudziesięciu jednostek.

Kiedy dzieci zaczynają łamać liczby?

Oddzielenie odbywa się w kluczowym etapie 1, aby dzieci wiedziały, że dwucyfrowa liczba składa się z dziesiątek i jedności. Chodzi o to, aby dziecko połączyło ze sobą strzałki, aby dopasować liczby. Są to dwie powszechnie stosowane metody dodawania dużych liczb.

Nauczyciel może zacząć uczyć dzieci dodawania dwucyfrowych i trzycyfrowych liczb w roku 3, dzieląc się na sekcje. Powodem tego jest to, że pomaga dzieciom mentalnie dodawać wielokrotności dziesięciu i wielokrotności 100. Dzieci w trzecim roku powinny również dodać, aby nauczyć się, jak dodawać trzycyfrowe liczby z pomocą, aby dziecko prawdopodobnie napotkało obie te metody.

Trzycyfrowy numer to numer, dla którego potrzebujesz trzech znaków. Zgadłeś już, że wszystkie liczby od 100 do 999 są trzycyfrowe. Zawierają jednostki, dziesiątki i setki.
Chłopaki, odpowiedzcie na pytanie: ile jest tam liczb trzycyfrowych?

Przykłady mnożenia liczby wielocyfrowej przez liczbę jednocyfrową

Weźmy przykład, aby dowiedzieć się, jak wykonać operację mnożenia. wielocyfrowa liczba na jedna cyfra .

Przede wszystkim pamiętaj o zasadzie mnożenia przez zero i jeden.
Ta reguła stanowi:
Liczba * 0 = 0
Liczba * 1 = liczba

Podział w mnożeniu

Dzieci trzeciego roku również muszą się rozmnażać liczby dwucyfrowe jednocyfrową liczbą. Zazwyczaj uczą się tej partycji, na przykład. Gdy nauczyciele będą bardzo pewni, że dziecko wie, jak pomnożyć wielokrotności dziesięciu i stu, często pozwolą dziecku przejść na szybszą metodę kolumnową.

W szóstym roku dzieci powinny zacząć obliczać. Aby to ułatwić, nauczyciel może pokazać im, jak podzielić liczby dziesiętne. Czytany jest jak cztery razy sześć równa się dwadzieścia cztery lub tylko cztery razy sześć - dwadzieścia cztery. Znajomość mnożenia jest bardzo ważna. Tak więc, jeśli masz słabość w mnożeniu, powinieneś spróbować osiągnąć poziom własności następującego „harmonogramu”.

Przykłady
5 * 0 = 0;
18 * 0 = 0;
4506 * 0 = 0
1 * 34 = 34;
2384 * 1 = 2384;
1 * 47586 = 47586

W przypadku mnożenia liczb wielowartościowych często stosuje się metodę mnożenia przez kolumnę, której użyjemy w naszych przykładach.

Pomnożyć liczbę wielocyfrową przez liczbę inną niż 0 lub 1.
Rozważ przykłady.
Weź liczby 348 i 4. Dla naszej wygody piszemy je w kolumnie. Rozpoczynamy mnożenie od prawej kolumny i mnożymy liczby 4 i 8. Otrzymujemy liczbę 32. Liczba 2 jest zapisana ściśle pod liczbami 8 i 4. 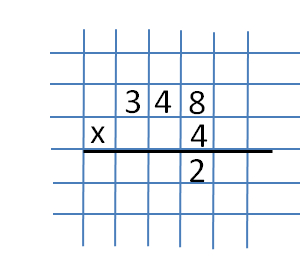I liczba 30 jest przenoszona na następną cyfrę (ranga kilkunastu). Podczas przenoszenia liczby na wyższą cyfrę, na przykład od jedności do dziesiątek, liczba ta traci 0. 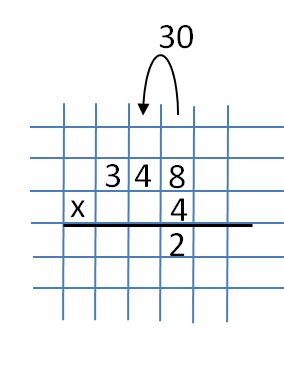Teraz pomnóż 4 i 4 i otrzymaj 16. Dodaj 3 z poprzedniego mnożenia. W rezultacie otrzymamy 19. Piszemy liczbę 9 pod liczbą 4 (po lewej stronie liczby 2) i tłumaczymy 1 na następną cyfrę (rozładowanie setek). Następnie pomnóż liczby 3 i 4 i dodaj 1 do wyniku z poprzedniej akcji. W rezultacie otrzymujemy 13. Zapisujemy to całkowicie, ponieważ to jest nasza ostatnia akcja. 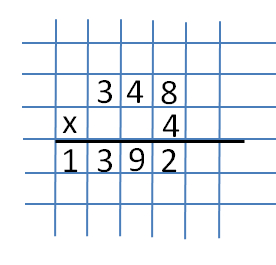W rezultacie otrzymujemy iloczyn liczb 348 o 4, co jest równe 1392.

Mnożenie dużych liczb

Twoja pewność siebie i umiejętność uczenia się matematyki w dużej mierze zależy od twojej wiedzy na temat reprodukcji. Dlatego powinieneś dążyć do radzenia sobie z powyższym „harmonogramem”.

• Produkt jest wynikiem pomnożenia dwóch liczb.
• Aby obliczyć 8 × 9, przywołaj „tabelę osiem razy”.

Aby pomnożyć dużą liczbę przez inną liczbę, możemy użyć krótkiego mnożenia lub długiego mnożenia.

Aby pomnożyć dużą liczbę przez liczbę jednocyfrową, wprowadź liczby w pionie, a większa liczba zostanie pomnożona przez mniejszą liczbę. Aby obliczyć 89 × 7, ustaw go pionowo z mniejszą liczbą umieszczoną pod większą liczbą, jak pokazano poniżej. Teraz oblicz 7 × 8 i dodaj 6, aby otrzymać to, jak pokazano poniżej.

Przykłady mnożenia liczby wielocyfrowej przez liczbę dwucyfrową

W tym przykładzie rozważamy mnożenie liczby trzycyfrowej przez dwucyfrową liczbę. Weź liczby 925 i 38.
Cały proces mnożenia jest podzielony na kilka części.
Pierwsza część to mnożenie liczby 925 przez liczbę 8. Dla wygody zapisujemy je w kolumnie.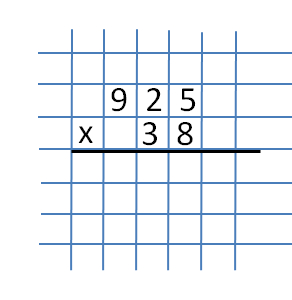
Jak zwykle, mnożąc się w kolumnie, zaczniemy nasze działania od prawej kolumny. Liczby 5 i 8 są tam zapisane, mnożąc je, co da nam liczbę 40. Piszemy cyfrę 0 pod liczbami 5 i 8. Nie zapomnij przenieść 40 na następny poziom (poziom dziesiątek). 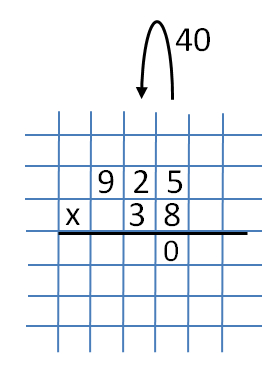Teraz pomnóż liczby 2 i 8. Dostajemy 16. Nie zapomnij dodać liczby 4, która pozostaje po poprzedniej akcji (gdy mnożymy 8 i 5). Otrzymujemy liczbę 20. Liczba 0 jest zapisana pod numerem 3 obok poprzedniego numeru 0, a 20 jest przenoszone do następnej cyfry (ranga setek). 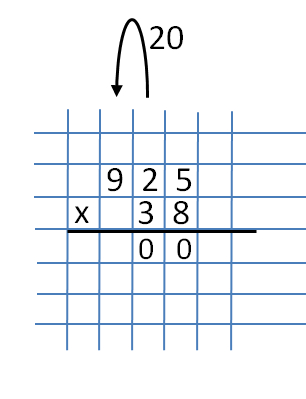A ostatnim działaniem pierwszej części jest mnożenie liczb 9 i 8. Wynikiem tych liczb jest 72. Dodaj do produktu liczbę 2 i otrzymamy liczbę 74. Zapisujemy to całkowicie.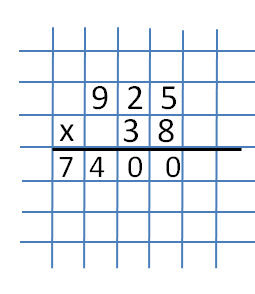
Druga część to mnożenie liczby 925 przez liczbę 3. Nie będziemy rozważać tej części w taki sam sposób jak poprzedni, ale po prostu wypisz wynik iloczynu tych liczb. 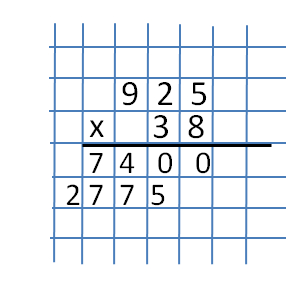Podczas rejestrowania iloczynu liczb drugiej części należy pamiętać, że nagranie należy rozpocząć nie z prawej kolumny, ale z przesunięciem o jedną. W naszym przykładzie pierwsza liczba musi być zapisana ściśle pod numerami 2, 3,0. Zobacz rysunek.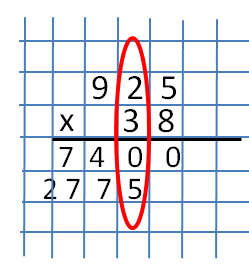
Trzecia część to uzyskanie sumy liczb. Jest to ostatni etap, w którym musimy uzyskać sumę z pierwszej pracy - 7400 i od drugiej pracy - 2775. Podsumowujemy, przestrzegając reguł, które są używane podczas dodawania do paska. 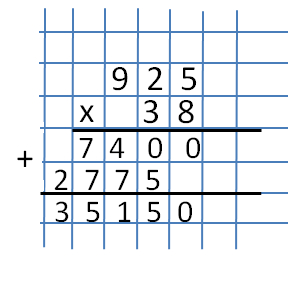Ostatnia cyfra pokazuje wynik pomnożenia dwucyfrowej liczby 38 przez trzycyfrową liczbę 925.

Najważniejsza zasada, z którą zaczynamy badać mnożenie w kolumnie:

Często podajemy rozwiązanie w następujący sposób. Mnożenie 38 przez 60 jest szybsze niż mnożenie przez 60 przez 38, ponieważ 60 zawiera zero. Mnożenie przez 385 przez 500 jest szybsze niż pomnożenie przez 500 przez 385, ponieważ 500 zawiera dwa zera. Aby pomnożyć dwa duże liczby , wpisz liczby w pionie, a większa liczba zostanie pomnożona przez mniejszą liczbę, która nazywa się mnożnikiem. Używamy tabeli czasów, aby znaleźć produkt większej liczby z każdą cyfrą w mnożniku, dodając wyniki. Na przykład, jeśli cyfra mnożąca jest w stu kolumnach, dodaj dwa zera dla kolumny dziesiątek i jednej kolumny.

• Więc umieść 3 w kolumnie jednostek i noś 6.
• Następnie oblicz 7 × 8 i dodaj 6, aby uzyskać 62.
• W kolumnie jednostki umieszczane jest zero.
• Następnie obliczamy 6 × 38, jak pokazano powyżej.
• W kolumnie jednostek umieszcza się zero, a także kolumnę dziesiątek.
• Następnie obliczamy 5 × 385, jak pokazano powyżej.
• Nie zapomnij dodać zera dla każdej wartości miejsca po cyfrze mnożącej.
• Aby pomnożyć 269 przez 78, miejsce 78 poniżej.
• Następnie obliczamy 8 × 269 i 70 × 269, jak pokazano powyżej.

Jest to znane jako przemienne prawo do mnożenia.

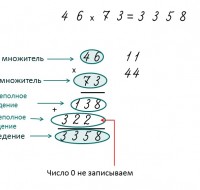
Przykład: 46 pomnóż przez 73

Pod liczbą 46 piszemy liczbę 73 zgodnie z zasadą:

Jednostki są zapisywane pod jednostkami, a dziesiątki pod dziesiątkami.

1 Pomnóż zaczynając od jednostek.

3 pomnóż przez 6. Okazuje się 18.

• 18 jednostek to 1 tuzin i 8 jednostek.
• Piszemy 8 jednostek pod jednostkami, a 1 dziesiątki są zapamiętywane i dodawane do dziesiątek.

Teraz 3 pomnóż przez 4 tuziny. Okazuje się 12.

Etykieta numer 1: Kwadratowe liczby w latach 50-tych

Każdy może być dobry w matematyce z etykietami Mike'a Bistera. Teraz, jeśli liczba z kroku 2 jest mniejsza niż 10, musisz umieścić zero przed nim.

Etykieta 2: pomnożenie dwóch liczb w latach 90-tych razem

Gdy pomnożymy dwie liczby w latach 90-tych, liczba w nawiasach obok każdej liczby wskazuje, jak daleko ta liczba jest daleka.

Pomnożyć liczbę trzycyfrową przez liczbę dwucyfrową.

To jedna z moich ulubionych sztuczek, ponieważ jest prosta i zadziwia każdego, kto ją widzi. Poproś kogoś, aby wybrał dwie liczby poniżej 10 i napisał jeden na drugim. Poproś osobę, aby je dodała i umieść odpowiedź bezpośrednio pod dwoma liczbami. Poproś osobę, aby kontynuowała dodawanie dwóch dolnych liczb do kolumny i kontynuuj sumowanie sumy, aż otrzymasz tylko dziesięć liczb. Następnie dodaj do niego całą kolumnę. Przykład: ktoś wybiera cyfry 4 i 7 i pisze 4 na górze. Następna liczba w serii będzie taka, że ​​4 7 = Następnie, dodając dwie dolne liczby do kolumny, następna liczba będzie wynosiła 18, ponieważ 7 11 = Musi to robić, dopóki nie będzie miał tylko dziesięciu liczb, a następnie doda wszystko kolumna.

12 tuzinów, a nawet 1, tylko 13 tuzinów.

W tym przykładzie nie ma setek, więc natychmiast piszemy setki zamiast setek.

138 to pierwsza praca częściowa.

2 mnożą dziesiątki.

7 tuzinów pomnożonych przez 6 jednostek otrzymuje 42 tuziny.

• 42 tuziny to 4 setki i 2 tuziny.
• 2 tuziny napiszą pod dziesiątkami. 4 pamiętaj i dodaj do setek.

7 tuzinów pomnożonych przez 4 tuziny otrzymało 28 setek. 28 setek, a nawet 4 okaże się 32 setki.

Kolumna może wyglądać mniej więcej tak. Szybko spojrzysz na liczby i powiesz mu, że wszystkie dziesięć numerów zostało dodanych. Wystarczy spojrzeć na 76 i dodać do niego dziesiątki cyfr, 76 7 = Następnie umieść 76 na jednym końcu. Jeśli osoba wybrała dwie duże liczby, takie jak 8 i 9, siódma liczba może być liczbą trzycyfrową. Kolumna będzie wyglądać następująco.

Jakie błędy można popełnić podczas mnożenia i jak ich unikać

Siódmy numer w tym przypadku. Tutaj przyjrzymy się, jak pomnożyć liczby dwucyfrowe. Początkowo używał metody zwanej metodą bezpośrednią Jakowa Traktenberga, a drugiej metodą „dwóch palców”. Obie te metody będą działać dla dowolnej kombinacji liczb dwucyfrowych.

• 32 setki to 3 tysiące 2 setki.
• Piszemy 2 setki w setkach, a zapamiętamy 3 tysiące i dodamy do tysięcy.

W tym przykładzie nie ma tysięcy, dlatego piszę 3 w miejscu tysięcy natychmiast.

3220 jest drugim niekompletnym produktem.

3 Złóż pierwszą i drugą niekompletną pracę zgodnie z zasadą dodania do kolumny.

138 plus 3220 to 3358.

Jeśli chcesz pomnożyć liczby do dwunastu, spójrz na nie. Metoda bezpośrednia jest rzadko nauczana w szkołach, ale znana jest od wieków. W szkole zazwyczaj uczymy się rejestrować wynik mnożenia każdej cyfry mnożnika przez pojedyncza linia a następnie suma całkowita.

Pomnóż przez pomnożenie

Zamiast tego piszesz tylko odpowiedź. Aby to zrobić, wykonaj kilka obliczeń na każdym kroku. Pary, które nie mają nic wspólnego, są ignorowane. Te pary nazywane są parami zewnętrznymi i wewnętrznymi. Para zewnętrzna zawsze łączy pojedynczą cyfrę mnożnika z cyfrą, w której się teraz znajdujemy. Wewnętrzna para zawsze łączy dziesiątki cyfr z cyfrą po prawej stronie cyfry, nad którą pracujemy w mnożniku.

Przeczytaliśmy odpowiedź: 46 pomnożone przez 73 wyniesie 3358

(Kliknij na zdjęcie)

Składniki akcji mnożenia

(Kliknij na zdjęcie)

Przykładowe rozumowanie
podczas nagrywania
mnożenie w kolumnie

Frakcja okresowa

Ta metoda jest zasadniczo taka sama jak w matematyce wedyjskiej, kiedy używają sutry „pionowej i poprzecznej” podczas mnożenia liczb dwucyfrowych. Styl równania to jedyna prawdziwa różnica. W matematyce wedyjskiej równanie jest napisane w dwóch wierszach, jak pokazano poniżej. Dla metody bezpośredniej równanie jest zgodne z odpowiedzią pod mnożeniem.

Możesz oglądać bezpośredni obraz mnożenia przy użyciu dwucyfrowych mnożników lub kontynuować czytanie następujących przykładów. Liczba zer wiodących zawsze pokrywa się z liczbą cyfr w mnożniku, więc przy mnożeniu przez liczby dwucyfrowe zawsze dodajemy 2 wysokie zera. Poniżej: mnożymy razem dwie pojedyncze cyfry.

Dokładnie przejrzyj i zastosuj w swoich działaniach!

Jakie błędy podczas mnożenia
może zrobić i
jak ich uniknąć

Spójrz uważnie

aby nie popełniać błędów!

Zasady dotyczące innych przypadków mnożenia

Pomnóż w kolumnie przez pojedynczą liczbę

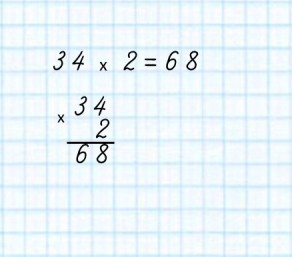
Ten krok polega na pomnożeniu dziesiątek cyfr jednej liczby przez liczbę jednostek innej. Podczas pisania równania w jednej linii, jeśli narysujemy zakrzywione linie łączące między liczbami pomnożonymi, otrzymamy parę zewnętrzną i parę wewnętrzną. Kiedy piszemy równanie na dwóch liniach, otrzymujemy krzyż, gdy rysujemy proste linie łączące między zwielokrotnionymi liczbami.

Mnożenie w kolumnie dwóch dodatnich liczb całkowitych o wielu wartościach

Dodając wyniki tych dwóch równań, otrzymujemy 14, więc piszemy 4 i przesyłamy. Na tym etapie mnożymy dziesiątki cyfr każdej liczby. Podczas pisania równania w jednej linii, zewnętrzna para na tym etapie jest podłączona do zera, więc wynik tej pary równa się zero i można go zignorować. W tym przykładzie obliczenia umysłowe, które musimy wykonać, są stosunkowo proste, a ponieważ podejmujemy mniej kroków niż tradycyjna metoda mnożenia, jest to szybsze. Wadą tego podejścia jest jednak wada, zwłaszcza gdy liczby są większe.

Ten przykład można zapisać w kolumnie.

Pod liczbą 34 piszemy liczbę 2 zgodnie z zasadą:

Pod numerem 68 piszemy liczbę 2 zgodnie z zasadą:

Pomnożymy razem dwie pojedyncze cyfry. Więc piszemy 2 i noszę. Tu jest ciężko, zwłaszcza jeśli próbujesz psychicznie wykonać obliczenia. Więc piszemy 4 i noszę. Mamy 63, do których dodajemy przeniesienie 14, aby nam dać. Piszemy 7 i nosimy.

Jak pomnożyć w kolumnie: podstawowe zasady

Zgodnie z oryginalną metodą i powodem wiodących zer, mamy dodatkowy krok ze względu na transfer. Mamy więc zero plus przeniesienie 7, które piszemy 7, co daje nam naszą odpowiedź. Ten krok może wydawać się zbędny i moglibyśmy po prostu zapisać przeniesienie w ostatnim kroku, ale gdy studiujesz metodę, lepiej postępować zgodnie z całym równaniem, dopóki nie będziesz wystarczająco zaznajomiony z metodą pobierania małych etykiet.

Jednostki są zapisywane pod jednostkami, a dziesiątki, jeśli są pod dziesiątkami.

1 Pomnóż zaczynając od jednostek.

2 razy 8. Okazuje się 16.

• 16 jednostek to 1 tuzin i 6 jednostek.
• 6 jednostek piszemy pod jednostkami. I będziemy pamiętać 1 tuzin i dodać do dziesiątek.

Teraz 2 pomnóż przez 6 tuzinów. Okazuje się 12.

12 tuzinów i 1 więcej tylko 13 tuzinów.

Jak widać, gdy liczby zawierają cyfry 7, 8 i 9, matematyka staje się bardziej złożona, zwłaszcza jeśli próbujesz to zrobić psychicznie. Jacob też to rozumiał i postawił sobie zadanie znalezienia łatwiejszego sposobu osiągnięcia tego. Wprowadź metodę „dwóch palców”, jak to nazwał, która upraszcza obliczenia, które musisz wykonać. Zanim przejdziemy do metody dwóch palców, musimy uzyskać dodatkowe informacje referencyjne dla jednokrotnego mnożenia.

Przykłady mnożenia liczby wielocyfrowej przez liczbę jednocyfrową

Podczas mnożenia dwóch cyfr przez jedną cyfrę wynik może być tylko jedną lub dwiema cyframi. Jeśli ustawimy zero przed wynikiem dowolnej cyfry, możemy przetworzyć wszystkie wyniki mnożenia dwóch liczb jedną cyfrą w postaci dwucyfrowych wyników, cyfr jednostek i dziesiątek cyfr.

• 13 tuzinów to sto trzydzieści więcej.
• 3 tuziny pism pod dziesiątkami. I będziemy pamiętać sto i dodać do setek.

W tym przykładzie nie ma setek, dlatego napisamy 1 natychmiast w miejsce setek.

Przeczytaliśmy odpowiedź : 68 pomnożone przez 2 wyniesie 136.