How to solve multiplication with a three-digit column. Multiplication by the bar. Multiply calculator

1. When do children start breaking numbers?
2. Examples of multiplying a multi-digit number by a single-digit number
3. Division in multiplication
4. Multiplication of large numbers
5. Examples of multiplying a multi-digit number by a two-digit number
6. Example: 46 multiply by 73
7. Label number 1: Square numbers in the 50s
8. Label 2: Multiplying two numbers in the 90s together
9. Multiply a three-digit number by a two-digit one.
10. What mistakes can be made when multiplying and how to avoid them
11. Multiply Multiply by Multiple
12. We read the answer: 46 multiplied by 73 will be 3358
13. Multiplication action components
14. Sample reasoning during recording multiplication in a column
15. What mistakes when multiplying can do and how to avoid them
16. Rules for other cases of multiplication
17. Multiplication in a column of two multi-valued positive integers
18. How to multiply in a column: basic rules
19. Examples of multiplying a multi-digit number by a single-digit number

Guys, let's repeat what a single-digit, two-digit and three-digit number is.

A single number is a number that requires one character to write.
For example: 1, 3, 5, 4, ...
Probably, you have already guessed that the digits are single digits when they are written as a number. They consist of units.

A two-digit number is a number that requires two characters to write. For example, all numbers from 10 to 99 are two-digit numbers. They consist of dozens and units.

When do children start breaking numbers?

The separation is carried out in key stage 1 so that the children know that the two-digit number consists of tens and ones. The idea is that the child joins the arrows together to match the numbers. These are two commonly used methods for adding large numbers.

The teacher can begin to teach children to add two-digit and three-digit numbers in year 3 by splitting into sections. The reason for this is that it helps children mentally add multiples of ten and multiples of 100. Children in the 3rd year should also add to learn how to add three-digit numbers with help, so your child will likely encounter both of these methods.

A three-digit number is a number for which you need three characters. You have already guessed that all numbers from 100 to 999 are three-digit. They contain units, tens and hundreds.
Guys, answer the question: how many three-digit numbers are there?

Examples of multiplying a multi-digit number by a single-digit number

Let's take an example to figure out how to perform the multiplication operation. multi-digit number on single digit .

First of all, remember the rule of multiplication by zero and one.
This rule states:
Number * 0 = 0
Number * 1 = Number

Division in multiplication

Children of the 3rd year also need to multiply double figures by a one-digit number. They are usually taught this partition, for example. Once teachers are very confident that the child knows how to multiply the multiples of ten and one hundred, they will often allow the child to switch to a faster column method.

In the 6th year, children should begin to calculate. To make it easier, the teacher can show them how to divide decimal numbers. It reads like four times six equals twenty four, or just four times six - twenty four. Knowledge of multiplication is very important. So, if you are weak in multiplication, you should try to reach the level of ownership of the following “time table”.

Examples
5 * 0 = 0;
18 * 0 = 0;
4506 * 0 = 0
1 * 34 = 34;
2384 * 1 = 2384;
1 * 47586 = 47586

For multiplication of many-valued numbers, the method of multiplication by a column is often used, which we will use in our examples.

Multiply a multi-digit number by a number other than 0 or 1.
Consider examples.
Take the numbers 348 and 4. For our convenience, we write them in a column. We start the multiplication from the rightmost column and multiply the numbers 4 and 8. We get the number 32. The number 2 is written strictly under the numbers 8 and 4. 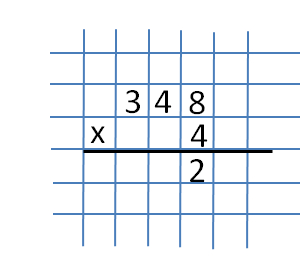And the number 30 is transferred to the next digit (the rank of a dozen). When transferring a number to a higher digit, for example, from ones to tens, this number loses 0. 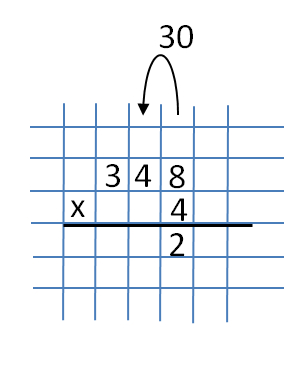Now multiply 4 and 4 and get 16. Add 3 from the previous multiplication. As a result, we will get 19. We write the number 9 under the number 4 (to the left of the number 2), and translate 1 into the next digit (the discharge of hundreds). 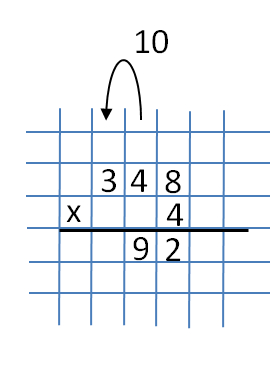Then multiply the numbers 3 and 4 and add 1 to the result from the previous action. As a result, we get 13. We write it down completely, because this is our last action. 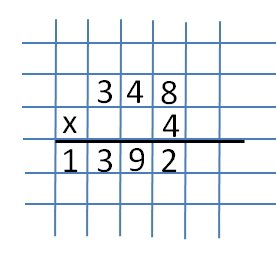As a result, we get the product of the numbers 348 by 4, which is equal to 1392.

Multiplication of large numbers

Your confidence and ability to learn mathematics will largely depend on your knowledge of reproduction. So, you should strive to cope with the above “time table”.

• The product is the result of multiplying two numbers.
• To calculate 8 × 9, recall the “table eight times.”

To multiply a large number by another number, we can use short multiplication or long multiplication.

To multiply a large number by a single-digit number, enter the numbers vertically, and the larger number will be multiplied by a smaller number. To calculate 89 × 7, set it vertically with a smaller number placed under the larger number, as shown below. Now, calculate 7 × 8 and add 6 to get it written as shown below.

Examples of multiplying a multi-digit number by a two-digit number

In this example, we consider the multiplication of a three-digit number by a two-digit one. Take the numbers 925 and 38.
The whole multiplication process is divided into several parts.
The first part is the multiplication of the number 925 by the number 8. For convenience, we write them in a column.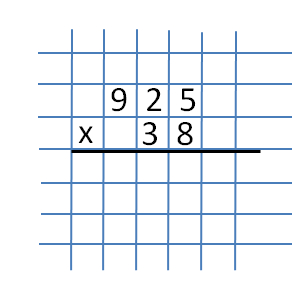
As usual, when multiplying in a column, we will begin our actions from the rightmost column. The numbers 5 and 8 are written there, multiplying them, which will give us the number 40. We write the number 0 under the numbers 5 and 8. Do not forget to transfer 40 to the next level (tens level). 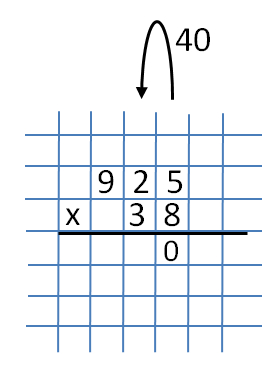Now multiply the numbers 2 and 8. We get 16. Do not forget to add the number 4, which remains after the previous action (when multiplying 8 and 5). We get the number 20. The number 0 is written under the number 3 next to the previous number 0, and 20 is transferred to the next digit (the rank of hundreds). And the last action of the first part is the multiplication of the numbers 9 and 8. The product of these numbers is 72. Add to the product the number 2 and we get the number 74. We write it down completely.
The second part is the multiplication of the number 925 by the number 3. We will not consider this part in the same way as the previous one, but simply write the result of the product of these numbers. 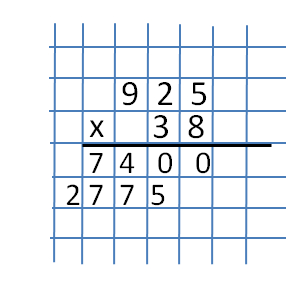When recording the product of the numbers of the second part, it must be remembered that the recording should be started not from the rightmost column, but with an offset of one. In our example, the first number must be written strictly under the numbers 2, 3,0. See the drawing.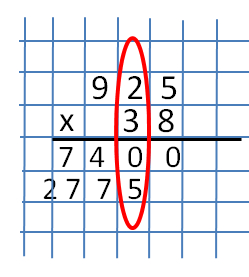
The third part is getting the sum of the numbers. This is the final stage at which we need to get the sum from the first work - 7400 and from the second work - 2775. We summarize, observing the rules that are used when adding to the bar. The last figure shows the result of multiplying a two-digit number 38 by a three-digit number 925.

The most important rule with which we begin to study the multiplication in a column:

We often state a solution as follows. Multiplying 38 by 60 is faster than multiplying by 60 by 38, since 60 contains zero. Multiplication by 385 by 500 is faster than multiplying by 500 by 385, since 500 contains two zeros. To multiply two large numbers , write the numbers vertically, and the larger number will be multiplied by the smaller number, which is called the multiplier. We use the table of times to find the product of a larger number with each digit in the multiplier, adding results. For example, if the multiplying digit is in a hundred column, add two zeros for the tens column and the one column.

• So, place 3 in the units column and carry 6.
• Then calculate 7 × 8 and add 6 to get 62.
• In the unit column, zero is placed.
• Then we calculate 6 × 38, as shown above.
• In the column of units zero is placed, as well as a column of tens.
• Then we calculate 5 × 385, as shown above.
• Do not forget to add a zero for each value of the place after the multiplying digit.
• To multiply 269 by 78, place 78 below.
• Then we calculate 8 × 269 and 70 × 269, as shown above.

This is known as Commutative Law for Multiplication.

Example: 46 multiply by 73

Under the number 46 we write the number 73 according to the rule:

The units are written under the units, and dozens under the tens.

1 Multiply starting with units.

3 multiply by 6. It turns out 18.

• 18 units are 1 dozen and 8 units.
• We write 8 units under the units, and 1 dozens is memorized and added to the tens.

Now 3 multiply by 4 dozen. It turns out 12.

Label number 1: Square numbers in the 50s

Anyone can be good at math with the labels of Mike Bister. Now, if the number from step 2 is less than 10, you must put a zero in front of it.

Label 2: Multiplying two numbers in the 90s together

When you multiply two numbers in the 90s together, the number in parentheses next to each number indicates how far this number is far from.

Multiply a three-digit number by a two-digit one.

This is one of my favorite tricks, because it is simple and amazes anyone who sees it. Ask someone to pick two numbers below 10 and write one on top of the other. Ask the person to add them and put the answer directly under the two numbers. Ask the person to continue adding the bottom two numbers to the column and continue summing the total until you have only ten numbers. Then add the whole column to it. Example: someone chooses numbers 4 and 7 and writes 4 on top. The next number in the series will be because 4 7 = Then, adding the bottom two numbers to the column, the next number will be 18, because 7 11 = He must continue to do this until he has only ten numbers, and then he will add all column.

12 dozen, and even 1, only 13 dozen.

There are no hundreds in this example, so we immediately write hundreds in place of hundreds.

138 is the first partial work.

2 multiply dozens.

7 dozen multiplied by 6 units get 42 dozen.

• 42 dozen is 4 hundreds and 2 dozen.
• 2 dozen write under the dozens. 4 remember and add to the hundreds.

7 dozen multiplied by 4 dozen get 28 hundreds. 28 hundreds, and even 4 it will turn out 32 hundreds.

The column might look something like this. You will quickly look at the numbers and tell him that all ten numbers are added. All you have to do is look at 76 and add dozens of digits to it, 76 7 = Then put 76 on one end. If a person has chosen two large numbers, such as 8 and 9, the seventh number can be a three-digit number. The column will look like this.

What mistakes can be made when multiplying and how to avoid them

Seventh number in this case. Here we look at how to multiply two-digit numbers. At first, he used the method called the Direct Method by Yakov Trakhtenberg, and the second by the “two fingers” method. Both of these methods will work for any combination of two-digit numbers.

• 32 hundreds are 3 thousand and 2 hundreds.
• We write 2 hundreds under hundreds, and we will remember 3 thousand and add to thousands.

There are no thousands in this example, therefore I write 3 in the place of thousands immediately.

3220 is the second incomplete product.

3 Fold the first and second incomplete works according to the rule of addition to the column.

138 plus 3220 will be 3358.

If you are interested in multiplying the numbers to twelve, take a look at them. The direct method is rarely taught in schools, but has been known for centuries. At school, you are usually taught to record the result of multiplying each digit of a multiplier by single line and then the sum total.

Multiply Multiply by Multiple

Instead, you write only the answer. To do this, you do a couple of calculations at each step. Couples that equate to nothing are ignored. These pairs are called external and internal pairs. An external pair always connects a single digit of the multiplier with the digit in which we are now looking. An internal pair always connects dozens of digits with the digit to the right of the digit we are working on in the multiplier.

We read the answer: 46 multiplied by 73 will be 3358

(Click on the picture)

Multiplication action components

(Click on the picture)

Sample reasoning
during recording
multiplication in a column

Periodic Fraction

This method is essentially the same as in Vedic mathematics, when they use the "vertical and transverse" sutra when multiplying two-digit numbers. The style of the equation is the only real difference. In Vedic mathematics, the equation is written in two lines, as shown below. For the direct method, the equation is in line with the answer under the multiplication.

You can watch a direct multiplication video using two-digit multipliers or continue reading the following examples. The number of leading zeros always coincides with the number of digits in the multiplier, so when multiplying by 2-digit numbers, we always add 2 high zeros. The following: we multiply two single digits together.

Carefully review and apply in your actions!

What mistakes when multiplying
can do and
how to avoid them

Look carefully

so as not to make mistakes!

Rules for other cases of multiplication

Multiply in a column by a single number

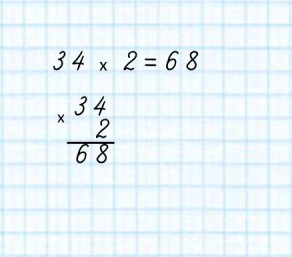
This step involves the multiplication of tens of digits of one number by the number of units of another. When writing an equation on one line, if we draw curved connecting lines between multiplied numbers, we get an outer pair and an inner pair. When writing an equation on two lines, we get a cross when we draw straight connecting lines between the multiplied figures.

Multiplication in a column of two multi-valued positive integers

Adding the results of these two equations, we get 14, so we write 4 and transfer. At this step, we multiply tens of digits of each number. When writing an equation on one line, the external pair at this step is connected to zero, so the result of this pair equals zero and can be ignored. In this example, the mental calculations that we need to do are relatively simple, and since we take fewer steps than the traditional multiplication method, this is faster. However, there is a drawback to this approach, especially when the numbers involved are larger.

This example can be written in a column.

Under the number 34 we write the number 2 according to the rule:

Under the number 68 we write the number 2 according to the rule:

We multiply two single digits together. So, we write 2 and carry. This is where it gets tough, especially if you are trying to mentally perform a calculation. So, we write 4 and carry. We have 63, to which we add a carry 14 to give us. We write 7 and carry.

How to multiply in a column: basic rules

Following the original method and the reason for the leading zeros, we have an extra step because of the transfer. So we have zero plus a carry 7, which we write 7, which gives us our answer. This step may seem redundant, and we could just write down the transference in the last step, but as you study the method, it’s better to follow the whole equation until you are familiar enough with the method to take small labels.

The units are written under the units, and tens, if they are under the tens.

1 Multiply starting with units.

2 times 8. It turns out 16.

• 16 units are 1 dozen and 6 units.
• 6 units we write under the units. And we will remember 1 dozen and add to the tens.

Now 2 multiply by 6 dozen. It turns out 12.

12 dozen and 1 more just 13 dozen.

As you can see, when the numbers contain the numbers 7, 8, and 9, the math becomes more complex, especially if you try to do it mentally. Jacob also understood this, and he set himself the task of finding an easier way to achieve this. Enter the “two fingers” method, as he called it, which simplifies the calculations you need to perform. Before moving to the two-finger method, we need to get additional reference information for one-bit multiplication.

Examples of multiplying a multi-digit number by a single-digit number

When multiplying two digits by one digit, the result can only be one or two digits. If we put a zero before the result of any digit, we can process all the results of multiplying two numbers with one digit in the form of two-digit results, digits of units and tens of digits.

• 13 dozen is 1 hundred and 3 dozen more.
• 3 dozen writing under the dozens. And we will remember one hundred and add to the hundreds.

There are no hundreds in this example, therefore we will write 1 immediately in the place of hundreds.

We read the answer : 68 multiplied by 2 will be 136.